
СПИНТех - Прикладная информатика / ЧМ_ЛР-4_Толстов_П-31
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное
учреждение высшего образования
Национальный исследовательский университет “МИЭТ”
Институт Системной и программной инженерии и информационных технологий
Дисциплина: Численные методы
Лабораторная работа №4
«Интерполяция функций»
Вариант 21
Выполнил:
Студент П-31
Толстов Д.В.
Преподаватель:
Лавров И.В.
Москва 2022
Задание:
Провести интерполяцию функции Рунге на отрезке [–1, 1] по формуле Лагранжа для n = 11 при равномерном распределении узлов интерполяции.
В отдельном файле (fr.m) записали функцию Рунге:
function y = fr(x) y = 1./(1 + 25 * x.^2); end |
Основной файл:
n = 11; a = -1; b = 1; h = (b - a) / (n - 1); x = a:h:b; yr = fr(x); X = a:0.01:b; N = length(X); Yr = fr(X); L = zeros(1, N); for i = 1:n l = ones(1, N); for j = 1:n if j ~= i l = l.*(X - x(j)) / (x(i) - x(j)); end end L = L + yr(i) * l; end plot(X, L, X, Yr, X, L-Yr) |
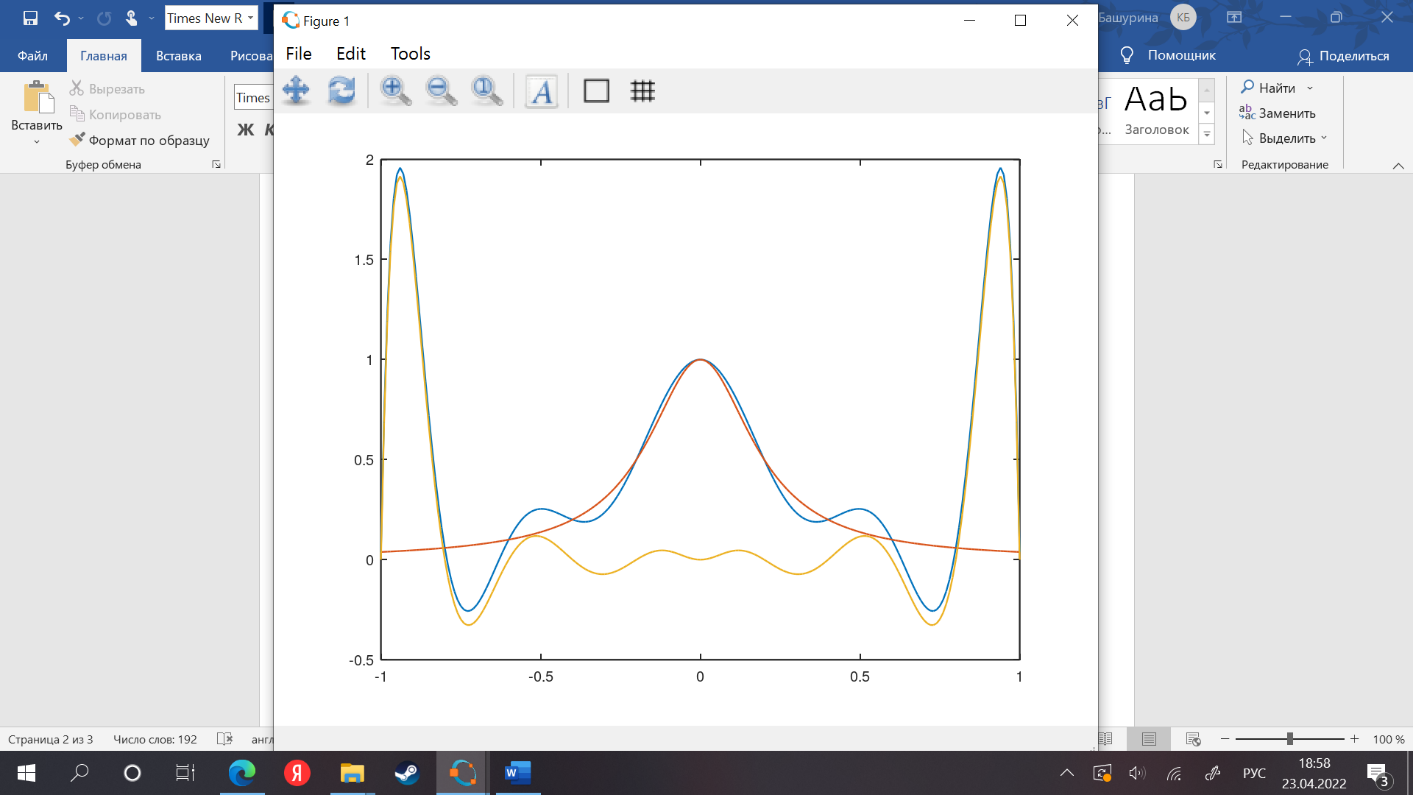
Провести интерполяцию функции Рунге на отрезке [–1, 1] по формуле Лагранжа для n = 11 для чебышевских узлов.
n = 11; a = -1; b = 1; h = (b - a) / (n - 1); for i=1:n x(i) = (a + b)/2 + ((b - a)/2)*cos((2*i + 1)*pi/(2*n + 2)); end yr = fr(x); X = a:0.01:b; N = length(X); Yr = fr(X); L = zeros(1, N); for i = 1:n l = ones(1, N); for j = 1:n if j ~= i l = l.*(X - x(j))./ (x(i) - x(j)); end end L = L + yr(i) * l; end plot(X, Yr, X, L, X, L-Yr) |

Построить графики функции Рунге и ее интерполянт не менее чем в 100 узлах. Сравнить результаты.
n = 100
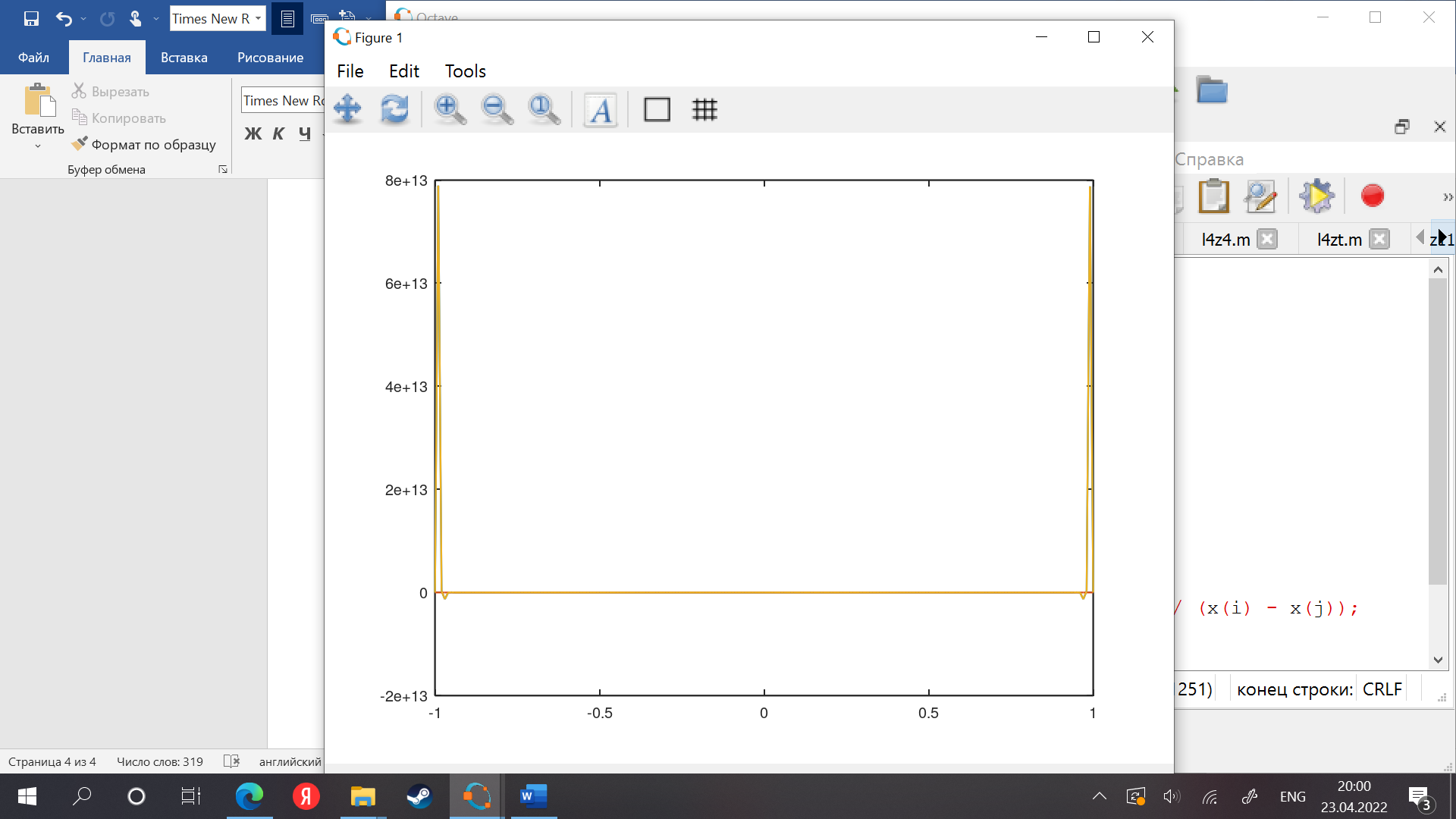
С увеличением порядка интерполирующего полинома при равномерном распределении узлов интерполяции на интервале [–1, 1] происходит ухудшение качества приближения на краях интервала.
Выбрать функцию согласно номеру компьютера и провести ее интерполяцию по формуле Лагранжа при равномерном распределении узлов на заданном интервале для n = 11 и n = 6.
![]()
Файл f.m:
function y = f(x) y = x.*((2*x.^2+1).^-1); end |
Основной файл:
n = 11; a = -1; b = 4; h = (b - a) / (n - 1); x = a:h:b; y = f(x); X = a:0.01:b; N = length(X); Y = f(X); L = zeros(1, N); for i = 1:n l = ones(1, N); for j = 1:n if j ~= i l = l.*(X - x(j)) / (x(i) - x(j)); end end L = L + y(i) * l; end plot(X, L, X, Y, X, L-Y) |
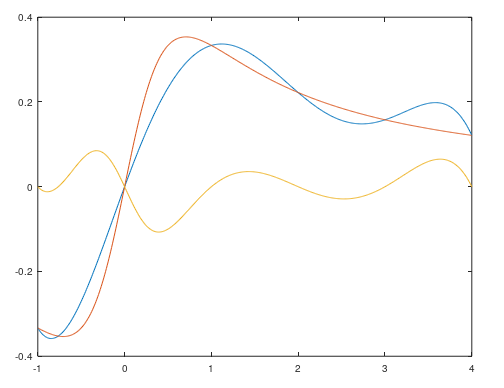
n = 11
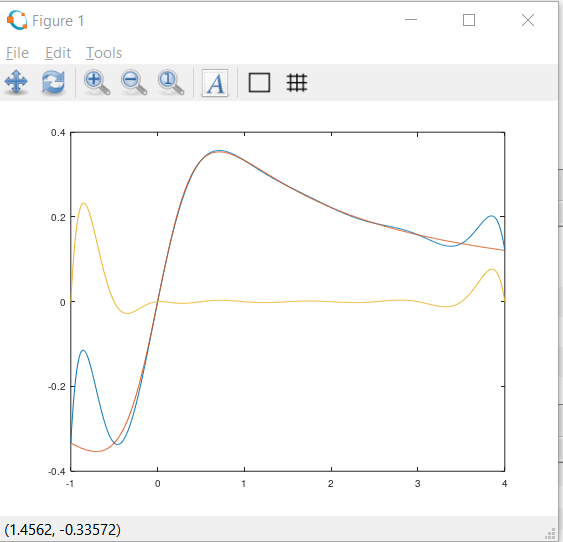
n = 6
Провести интерполяцию по тем же узлам, используя стандартные функции Matlab.
n = 11; a = -1; b = 4; h = (b - a) / (n - 1); x = a:h:b; y = f(x); X = a:0.01:b; Y = f(X); ap = polyfit(x, y, n); P = polyval(ap, X); plot(X, P, X, Y, X, P-Y) |
n = 11
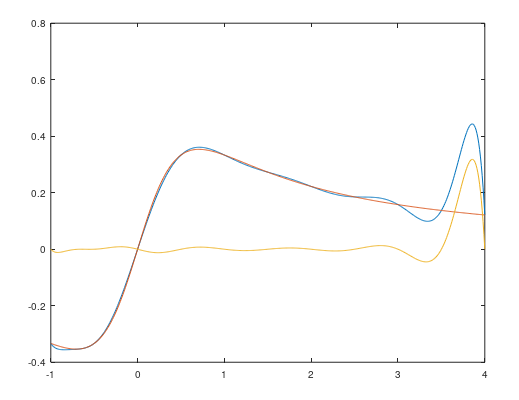
n = 6
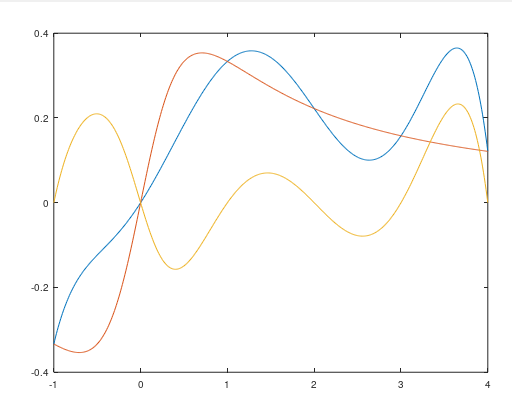
Построить графики исходной функции и интерполянт не менее чем в 100 узлах. Сравнить результаты.
n = 100; a = -1; b = 4\; h = (b - a) / (n - 1); x = a:h:b; y = f(x); X = a:0.01:b; N = length(X); Y = f(X); L = zeros(1, N); for i = 1:n l = ones(1, N); for j = 1:n if j ~= i l = l.*(X - x(j)) / (x(i) - x(j)); end end L = L + y(i) * l; end plot(X, L, X, Y, X, L-Y) |
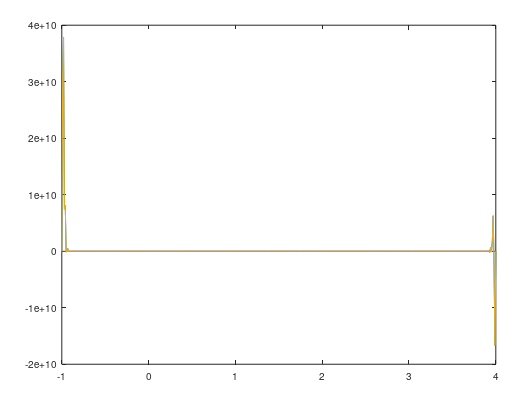
На краях интервала снова произошло ухудшение качества приближения. Более точный результат дала интерполяция для 11 узлов.
Вывод: мы изучили методы решения задачи интерполяции; приобрели навыки программирования методов интерполяции и использования стандартных средств системы Matlab для проведения интерполирования.
