
ДЗ. Оптимизация предварительного натяга подшипников шпиндельного узла
.pdf
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский государственный технический университет имени Н.Э. Баумана
(национальный исследовательский университет)» (МГТУ им. Н.Э. Баумана)
ФАКУЛЬТЕТ МАШИНОСТРОИТЕЛЬНЫЕ ТЕХНОЛОГИИ
КАФЕДРА МЕТАЛЛОРЕЖУЩИЕ СТАНКИ
Домашнее задание
по дисциплине: Методы обеспечения надёжности станков
на тему: Оптимизация предварительного натяга подшипников шпиндельного узла
Студент: Сергеев П.С.
Группа: МТ1-31М
Преподаватель: Зайцев А.Н.
Москва
2023
Оглавление |
|
Введение................................................................................................................... |
3 |
Влияние множества параметров на характеристики подшипника при |
|
предварительном натяге. ........................................................................................ |
4 |
Распределение внутренней нагрузки в шарикоподшипнике........................... |
4 |
Проскальзывание шариков подшипника ........................................................... |
7 |
Моделирование шпиндельной системы и анализ влияния преднатяга |
|
подшипников ........................................................................................................... |
8 |
Моделирование повышения температуры подшипников шпинделя ............. |
9 |
Анализ проскальзывания шариков подшипника ............................................ |
13 |
Определение предварительной нагрузки подшипников................................... |
15 |
Определение предварительного натяга подшипника..................................... |
15 |
Измерение повышения температуры подшипника ........................................ |
15 |
Условные обозначения: ........................................................................................ |
16 |
2

Введение
Шпиндель является основным компонентом большинства металлоре-
жущих станков, и его динамические характеристики оказывают значительное влияние на качество поверхности детали и точность станка. С развитием вы-
сокоскоростной обработки, особенно высокоскоростного фрезерования, си-
ловое резание на низкой скорости и скоростное резание часто выполняются одним шпинделем станка. Таким образом, необходимыми характеристиками являются высокая жёсткость при низкой скорости, а также низкое повыше-
ние температуры при высокой скорости. Чтобы обеспечить подходящую ско-
рость вращения для различных процессов обработки, шпиндель одного стан-
ка должен работать в широком диапазоне скоростей. Исходя из конструкции шпинделя, очевидно, что состояние подшипников, более чем других компо-
нентов, тесно связано с динамическими характеристиками шпинделя, в част-
ности, с жёсткостью подшипников, повышением температуры и усталостным износом тел качения подшипника.
Предварительный натяг шарикоподшипников обычно применяется для получения высокой жёсткости, подавления вибраций и повышения точности вращения шпинделя станка. Методы определения оптимального предвари-
тельного натяга подшипника имеют большое значение.
3
Влияние множества параметров на характеристики подшипника при предварительном натяге.
Распределение внутренней нагрузки в шарикоподшипнике.
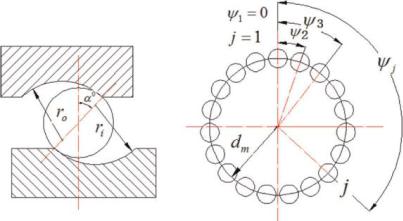
Упрощенная схема радиально-упорного шарикоподшипника показана на рисунке 1. На рисунке показан угол свободного контакта, который пред-
ставляет собой угол между любыми двумя линиями, перпендикулярными оси вращения подшипника, проходящими через точки контакта шарика и дорож-
ки качения. Угол свободного контакта 0 может быть описан следующим образом.
|
|
+ |
− |
|
|
0 = cos−1 (1 − |
|
|
|
) |
(1) |
|
|
|
|||
|
|
|
|
||
Рисунок 1 – Упрощенная схема радиально-упорного шарикоподшипника
При нулевом предварительном натяге подшипника:
|
|
+ − 1 |
|
= |
|
|
(2) |
|
|
||
|
|
|
|
|
|
|
|
Когда предварительный натяг подшипника не равен нулю, на шарик действу-
ет центробежная сила, и линия, проходящая через точки контакта шарика и дорожки качения, смещается, как показано на рисунке 2. Центр кривизны внутренней канавки дорожки качения перемещается от к 0. Центр кри-
визны внешней канавки дорожки качения остаётся неподвижным, а центр шарика перемещается от к 0.
4
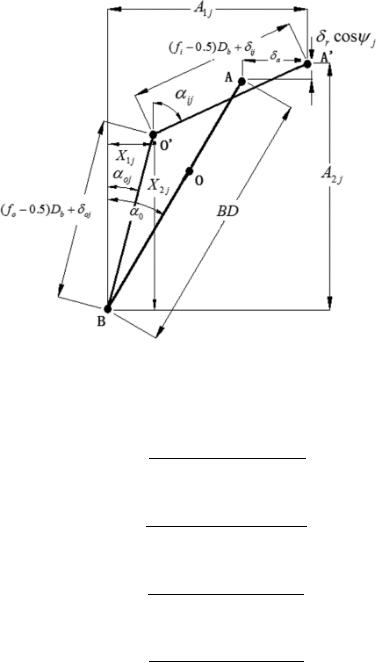
Рисунок 2 – Относительные положения центра шарика и дорожки качения центров кривизны канавок
Новый угол контакта может быть определен следующим образом:
2
cos = ( − 0,5) × +
1
sin = ( − 0,5) × +
2 − 2
cos = ( − 0,5) × +
2 − 2
sin = ( − 0,5) × +
где: 1 = × sin + ;
2 = × cos + × cos Ψ ;
1 и 2 – вспомогательные параметры.
(3)
(4)
(5)
(6)
Механический анализ подшипника проводится для составления урав-
нения баланса подшипника. Сила, приложенная к каждому шарику в под-
шипнике, показана на Рисунок 3.
5
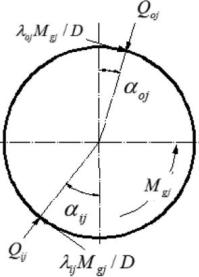
Рисунок 3 – Сила, приложенная к каждому шарику
Можно получить уравнения баланса шариков:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
× sin |
|
− |
|
× sin − |
|
|
× ( |
|
× cos |
− |
|
× cos |
) (7) |
||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где: |
|
= |
|
× 1,5; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= |
|
× 1,5 |
; |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
⁄ |
= 2,15 × 105 × (∑ |
)−1⁄2 × ( )−3⁄2. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
⁄ |
|
|
|
|
|
|
|
|
|||
Уравнения равновесия всего подшипника можно сформулировать сле-
дующим образом:
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
− ∑ ( |
× sin |
|
− |
|
|
|
× cos |
|
) = 0 |
(8) |
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
− ∑ ( |
× cos − |
|
|
|
|
|
× sin |
) × cos Ψ = 0 |
(9) |
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=1
Для расчета внутренних нагрузок подшипника необходимо определить значения , , , , 1, 2, 1 и 2 при каждом положении шарика, а так-
же относительные деформации внутреннего и наружного колец, и , с
помощью нелинейных уравнений. После определения этих параметров мож-
но рассчитать рабочее состояние подшипника.
6
Проскальзывание шариков подшипника
Проскальзывание шариков в подшипнике приводит к неправильным вибрациям шпинделя и сильному повышению температуры подшипника, и
его необходимо избегать. Центробежная сила шарика и площадь контакта уменьшаются с увеличением скорости вращения. Таким образом, эффект проскальзывания шарика в подшипнике увеличивается в результате умень-
шения площади контакта. Кроме того, шарик и дорожки качения теряют кон-
такт при определенной скорости вращения подшипника. При проскальзыва-
нии шариков увеличивается трение, что приводит к выделению большого ко-
личества тепла. При определенном осевом предварительном натяге подшип-
ника существует критическая скорость, при которой площадь контакта равна нулю. Критерий для заноса подшипника:
|
|
|
|
× sin ( |
|
) ≤ 10 |
(10) |
|
|||
|
3 |
|
|
|
|
||
где – контактная нагрузка между внутренней дорожкой качения и шари-
ком;
– угол контакта между внутренней дорожкой качения и шариком;
3 – центробежная сила шарика.
7
Моделирование шпиндельной системы и анализ влияния пред-
натяга подшипников
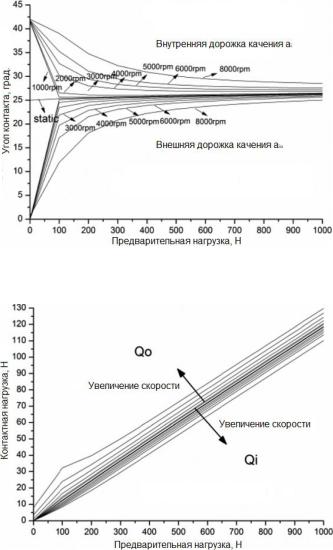
Углы контакта между шариком и дорожками качения увеличиваются с ростом преднатяга подшипника. Угол контакта между шариком и внутренней дорожкой качения уменьшается с увеличением скорости вращения подшип-
ника, а угол контакта между шариком и внешней дорожкой качения увеличи-
вается с увеличением скорости вращения подшипника. Углы контакта внут-
реннего и наружного колец стремятся к постоянству, приближаясь к углу контакта в статических ситуациях. Контактные нагрузки дорожек качения выглядят достаточно линейными, а осевая деформация медленно увеличива-
ется со скоростью вращения подшипника.
Рисунок 4 – и в зависимости от преднатяга и частоты вращения шпинделя
Рисунок 5 – и в зависимости от преднатяга и частоты вращения шпинделя
8
Моделирование повышения температуры подшипников шпинделя
Выделение тепла в подшипниках. В традиционном шпинделе основ-
ным источником тепла является подшипник. Большая часть тепла резания отводится охлаждающей жидкостью, поэтому тепло, выделяемое подшипни-
ками, является доминирующим теплом, вызывающим тепловые деформации.
После вычисления данных о рабочем состоянии подшипника, тепло, выделя-
емое подшипником, может быть вычислено с помощью уравнения:
= 1,047 × 10−4 |
× × |
(11) |
|
|
|
где – скорость вращения подшипника; |
|
|
– общий момент трения подшипника; |
|
|
- выделяемое тепло. Момент трения представляет собой сумму трех моментов: момент из-за приложенной нагрузки 1; момент из-за вязко-
го трения ; момент из-за вращательного движения в зоне контакта |
. |
|
0 |
( ) |
|
Крутящий момент, обусловленный приложенной нагрузкой, может |
||
быть эмпирически аппроксимирован следующим уравнением: |
|
|
1 = 1 × 1 × |
(12) |
|
где 1 – коэффициент, зависящий от конструкции подшипника и относи-
тельной нагрузки;
1 – эквивалентная динамическая нагрузка;
– диаметр делительной окружности.
Крутящий момент из-за вязкого трения зависит от типа подшипника,
скорости вращения и типа смазки. Для подшипников, работающих на уме-
ренных скоростях при несильной нагрузке, момент вязкого трения может быть эмпирически выражен следующим образом:
≥ 2000, |
= 10−7 × |
× ( )2⁄3 × 3 |
(13) |
||
0 |
|
0 |
|
|
|
≤ 2000, |
= 160 × 10−7 × |
× 3 |
(14) |
||
|
0 |
|
0 |
|
|
9
где 0 – коэффициент, зависящий от типа подшипника и режима смазки;
– динамическая вязкость смазочного материала при рабочей темпера-
туре.
Вращающий момент трения, возникающий при вращательном движе-
нии шарика, может быть выражен как:
|
3 × × |
× |
× |
|
= |
⁄ |
⁄ |
⁄ |
(15) |
|
|
|
||
( ) |
|
8 |
|
|
|
|
|
|
Таким образом, полный момент трения, возникающий при вращатель-
ном движения шарика может быть получен как:
|
= × |
+ × |
(16) |
|
( ) |
( ) |
|
Теплоотводы в шпинделе. Теплоотводы шпинделя создают конвек-
цию между валом и воздухом, внутренней частью корпуса и воздухом, а так-
же окружающим воздухом. Они обеспечивают тепловое сопротивление меж-
ду наружным кольцом подшипника и корпусом, а также внутренним кольцом подшипника и валом. Наконец, они создают теплопроводность между раз-
личными компонентами.
Конвекция между валом и воздухом определяется следующим обра-
зом:
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
= |
|
|
(17) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
где |
= 0,133 × 2⁄3 |
× 1⁄3 |
; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
= |
× |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– диаметр вала;
– число Прандтля воздуха;
– скорость воздуха на поверхности вала;
– коэффициент вязкости воздуха;
10
