§2. Выпуклое множество допустимых значений вектора варьируемых параметров

Широкий класс методов оптимизации ориентирован на решение задач оптимизации, у которых множество допустимых значений вектора варьируемых параметров является выпуклым множеством.

Множество D называется выпуклым множеством, если для любых точек и для любоговыполняется соотношение(рисунок 1). В противном случае множество допустимых значенийD называется не выпуклым множеством (рисунок 2).

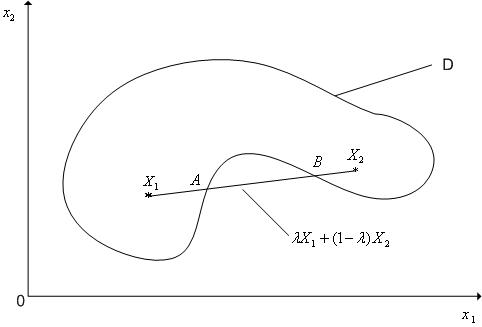
Рисунок 1 - К определению выпуклого множества (n=2). Все точки отрезка принадлежат множествуD

Рисунок 2 - Пример не выпуклого множества (n=2). Часть отрезкане принадлежат множествуD

Множество будем называтьотрезком с концами и обозначать.

На основе введенного понятия, можно дать другое определение выпуклого множества D. Множество допустимых значений вектора варьируемых параметров D называется выпуклым множеством, если оно наряду с любыми точками содержит в себе также отрезок.

Из определения следует, что все евклидово пространство является выпуклым множеством.

Легко показать, что любой отрезок в пространствеявляется выпуклым множеством.

Из курса аналитической геометрии известно, что в пространстве уравнение

(1)

определяет гиперплоскость. Здесь некоторые константы.

Теорема 1. Гиперплоскость является выпуклым множеством в пространстве.

Доказательство. Уравнение (1) перепишем в виде скалярного произведения

, (2)

где n-мерный вектор . Возьмем произвольные точки, удовлетворяющие уравнению (2):,. Рассмотрим некоторую точку, принадлежащую отрезку. По свойствам скалярного произведения имеем

.

Это означает, что точка X принадлежит гиперплоскости (2)●

Очевидно, что в пространстве уравнения (1), (2) определяют прямую, а в пространстве- плоскость.

Опять же из курса аналитической геометрии известно, что в пространстве неравенство

(3)

определяет полупространство. Здесь также некоторые константы.

Теорема 2. Полупространство является выпуклым множеством в пространстве●

Для доказательства выпуклости множеств часто бывает полезна следующая теорема.

Теорема 3. Пересечение любого конечного числа выпуклых множеств является выпуклым множеством.

Доказательство. Пусть – совокупность p выпуклых множеств пространства . Рассмотрим множество

,

являющееся пересечением множеств совокупности . Пусть точкипринадлежат множеству. Тогда они также принадлежат каждому из множеств. Так как множествовыпукло, то точкапринадлежит этому множеству. Поскольку множествовыбрано произвольно, то точкапринадлежит множествуD●

Из теоремы 4 следует, что выпуклыми множествами являются, например, следующие множества:

• гиперпараллелепипед ;

• симплекс ;

• выпуклый многогранник в пространстве , определяемый системой неравенств (каждое из которых задает полупространство)

……

.

В последних выражениях принято, что ,

Покажем в заключение, что гипершар

, (4)

является выпуклым множеством (r>0).

Известно, что евклидова норма n-мерного вектора X есть

.

Поэтому неравенство (4) можно переписать в виде , гдеn-мерный вектор . Пусть произвольные точкипринадлежат гипершару (4) и. Тогда по свойству нормы имеем

.

Входные термины:

• область допустимых значений вектора управляемых (варьируемых) параметров (переменных).

Выходные термины:

• критерий оптимальности, функция цели, целевая функция, критерий эффективности, функция полезности;

• детерминированная задача оптимального проектирования (оптимизации); задача оптимизации;

• стохастическая задача оптимального проектирования (оптимизации);

• оптимальное значение вектора управляемых (варьируемых) переменных (параметров);

• наименьшее значение критерия оптимальности.