ANSYS

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВОДНОГО ТРАНСПОРТА

Александр Юрьевич Шаманин

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРАКТИЧЕСКИМ РАБОТАМ ПО ДИСЦИПЛИНЕ ПРОЧНОСТЬ КОРАБЛЯ

РАСЧЕТЫ КОНСТРУКЦИЙ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ В ANSYS

Москва, 2012

2

УДК 004.942

А.Ю. Шаманин. Методические указания к практическим работам по дисциплине прочность корабля. Расчеты конструкций методом конечных элементов в ANSYS. - МГАВТ, 2012-77с.

Настоящее учебно-методическое пособие предназначено для студентов очного и заочного обучения специальности «180100 Кораблестроение и океанотехника». Может быть полезным для аспирантов, инженерно-технических и научно-педагогических работников, специализирующихся в области расчетов конструкций методом конечных элементов.

Основная цель пособия - получить навыки работы с программным комплексом ANSYS и дать общее представление о возможностях программного комплекса ANSYS.

Описаны алгоритмы решения, наиболее распространенных в практике судостроения, задач в ANSYS. Приведены задания для практических работ по курсу «Прочность судовых конструкций».

Материал, изложенный в пособии, в течение ряда лет апробирован на кафедре Судостроение и судоремонт Московской государственной академии водного транспорта.

© Московская государственная академия водного транспорта, 2012 г.

© А. Ю. Шаманин, 2012 г.

3

Содержание

4

1. Введение в МКЭ

Метод конечных элементов (МКЭ) — численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела (сопромата), теплообмена, гидродинамики и электродинамики.

Википедия (http://www.wikipedia.org/)

1.1.Метод Конечных Элементов

1.1.1. История развития метода

Возникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах. Основоположником теории МКЭ считается Р. Курант (1943 г.), но из-за нахождения вычислительной техники в зачаточном состоянии метод не получил развития, поэтому впервые был применён на ЭВМ лишь в 1944 году Аргирисом. Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать как один из вариантов распространённого в строительной механике метода Рэлея — Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах, могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений. Более полно история возникновения метода коечных элементов отражена в [1], [2].

С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты прочности проводят, используя МКЭ.

1.1.2. Основы метода конечных элементов

Инженерные конструкции представляют совокупность конструктивных элементов (балки, стержни, пластинки, оболочки), соединенные в конечном числе узлов. В сплошной среде, количество точек связи и количество составных элементов (в металле – зерен) бесконечно, именно это и осложняет решение задач в сплошной среде. Введенное Тёрнером и др. [2] понятие конечный элемент, позволяет преодолеть эту трудность путем разбиения сплошного тела на конечные элементы (исчислимого количества),

5

взаимодействующие между собой только в точках соединения элементов (в узлах), в которых вводятся фиктивные силы, эквивалентные поверхностным напряжениям, распределенным по границам элементов. В случае принятия такой идеализации, задача сводится к обычной задаче строительной механики, которая может решаться численно.

Основная идея МКЭ состоит в том, что любую непрерывную в некоторой области величину (например, внутреннее усилие в конструкции, перемещение и т.п.) можно аппроксимировать дискретной моделью, которая создается из множества кусочнонепрерывных функций, определенных в конечном числе подобластей (элементов). Обычно такими функциями являются полиномы – линейные, квадратичные, кубичные и т.д. Кусочно-непрерывные функции строятся с помощью значений непрерывной величины в узлах. Таким образом, чтобы определить неизвестную непрерывную вели чину, нужно определить ее значения в узлах.

Основные этапы создания дискретной модели неизвестной величины следующие:

1.В исследуемой области задается конечное число точек (узлов).

2.Значения непрерывной величины в каждом узле считаются неизвестными, они должны быть определены.

3.Исследуемая область разбивается на конечное число подобластей (элементов), имеющих общие точки (узлы).

4.Непрерывная величина в каждом элементе аппроксимируется полиномом, который определяется с помощью узловых значений этой величины: для каждого элемента определяется свой полином, но его коэффициенты подбираются так, чтобы сохранялась непрерывность величины на каждой границе элемента

1.2.Уравнения МКЭ

Вобщем виде, для созданной конечно-элементной модели, состоящей из n элементов и m узлов, составляются матрицы1:

Матрица сил возникающих в узлах, где – подматрица-столбец, с количеством элементов равным количеству степеней свободы узла.

12 { } = 3

[ ]

Перемещения узлов, где − подматрица-столбец, с количеством элементов равным количеству степеней свободы узла.

12 { } = 3

[ ]

1 Для понимания дальнейшего материала необходимо знание основ матричной алгебры. Необходимые сведения содержатся в главе 1.4.

6

Матрица жесткости (квадратная матрица), где – квадратные подматрицы размерности × , а – число компонент силы в рассматриваемых узлах.

{ } – силы, уравновешивающие действующие на элемент распределенные нагрузки; { } – силы в узлах обусловленные начальными деформациями.

Для упругого элемента основное соотношение может быть записано в виде

{ } = { } × { } + { } + { }

Или для напряжений:

{ } = { } × { } + { } + { }

{ } – напряжения в узлах; { } – матрица напряжений элемента;

{ } – матрица перемещений узлов; { } – напряжения возникающие в узлах от действия внешних нагрузок;

{ } – напряжения в узлах обусловленные начальными деформациями.

1.3. Элементы матричной алгебры

Матрица (математика) — система элементов , расположенных в виде прямоугольной таблицы.

Википедия (http://www.wikipedia.org/)

Матрицей размером m n называют совокупность m n чисел расположенных в виде таблицы состоящей из m строк и n столбцов и записанных в виде:

Элементы матрицы – это числа ( i 1, 2,..., m, j 1, 2,..., n ) составляющие её, где i

– номер строки, j – номер столбца на пересечении которых находится элемент матрицы.

Основные операции над матрицами

Сложение и вычитание матриц

Определяется для матриц одинакового размера. Суммой (разностью) матриц A и B, обозначаемой A+B (A-B), называется матрица C, элементы которой определяются по формуле: cij=aij+bij ( aij-bij), где aij и bij – соответственно элементы матриц A и B.

7

Умножение матрицы на число

Произведением матрицы A и числа , обозначаемым A, называется матрица B той же размерности, элементы которой bij=aij, где aij элементы матрицы A, т.е. при умножении матрицы на число надо все элементы матрицы умножить на это число.

Свойства

Пусть A, B, C – матрицы одного размера, , любые действительные числа, тогда:

1.A+ B= B+ A

2.(A+ B)+ C= A+(B+ C)

3.(A+B)= A+ B

4.( + )A= A+ A

5.( )A= ( A)

Матрица, все элементы которой равны нулю называется нулевой. Пусть O – нулевая матрица, тогда:

6.A+ O= A

(-1)A – противоположная к A и обозначается – A. 7. A+(- A)= O.

Транспонирование матриц

Матрица AT, полученная из данной матрицы A заменой её строк столбцами с теми же номерами называется транспонированной:

Умножение матриц

Произведением матриц Am n и Bn p называется матрица Cm p= A B (или проще AB),

AB существует только в том случае, когда первый множитель A имеет число столбцов, равное числу строк второго множителя B.

Свойства умножения

1.AB BA даже если оба произведения определены, но существуют матрицы A,B, такие что AB= BA, тогда они называются перестановочными.

Матрица E вида:

квадратной матрицей того же размера, т.е. AE=EA=A.

2.Умножение матриц ассоциативно, т.е. если определены произведения AB и (AB)C, то

определены BC и A(BC) и выполняется равенство:

(AB)C=A(BC).

3.Умножение матриц дистрибутивно по отношению к сложению, т.е.:

8

A(B+C)=AB+AC (A+B)C=AC+BC.

4.Для любого числа :

(AB)=( A)B=A( B).

5.Если существует AB, то определено (существует) BТAТ и выполняется равенство:

(AB)Т= BТAТ.

Обратная матрица

Матрица X, удовлетворяющая вместе с заданной матрицей A равенствам XA=AX=E, называется обратной к A и обозначается A-1.

1.4. Типы конечных элементов

Существует большое количество разнообразных типов конечных элементов позволяющих моделировать различные физические задачи (в программе ANSYS – около 200 видов конечных элементов1).

Задача разбиения тела на конечные элементы неоднозначна. В некоторых случаях (например, в случае расчета ферм) конструктивные элементы совпадают с конечными элементами (балки, стержни). В этих случаях, моделирование конструкции не представит особого труда и будет состоять в выполнении некоторого объема работы по стандартным правилам. Гораздо сложнее выполнить эту операцию для двумерных или трехмерных областей/тел. Здесь, прежде всего, нужно выбрать тип (или типы) конечных элементов (2х или 3х мерные), наилучшим образом аппроксимирующие исследуемую область. Плоские двумерные элементы применяются, в основном, для моделирования мембран, тонких пластин, тонкостенных оболочек и т. п. Объемные трехмерные элементы применяются, в основном, при исследовании полей температур, деформаций напряжений в массивных телах и т. п. [3], [4].

1.5. Уравнение МКЭ для балок

В качестве примера рассмотрим решение с применением МКЭ наиболее распространенной и в тоже время простой задачи Строительной механики корабля, расчет прочности балочной конструкции.

Балка - одномерный, геометрический элемент произвольного поперечного сечения. Основным различием между балкой и стержнем является тип воспринимаемой нагрузки (балки подвергаются воздействию поперечной нагрузки: поперечные силы, распределенные нагрузки и моменты, которые приводят к поперечной деформации балки).

1 Более подробно о конечных элементах, применяемых в ANSYS, можно прочитать в [3].

9

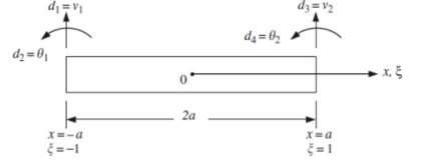
Узел конечного элемента имеет две степени свободы в: отклонение в поперечном направлении оси y (направление v) и вращение в плоскости осей x-y, θz (относительно оси Z). В итоге, балочный элемент (с двумя узлами по концам) имеет 4 степени свободы.

Рисунок 1- Балочный конечный элемент

1.5.1. Функции формы

Рассмотрим конечный элемент длиной l=2a с узлами 1 и 2 по концам, как показано на Рисунок 1Рисунок 1. Ось X определяет локальную систему координат элемента, начало оси находится посередине балки в центре среднего поперечного сечения балки.

Для каждой степени свободы конечного элемента балки можно составить уравнения равновесия, получим четыре функции формы. Удобнее когда функции формы определены относительными координатами в локальной системе координат. В относительной системе координат элемент определяется координатами -1 и +1, как показано на Рисунок 1.

Отношение между натуральной системой координат и локальной системой

где 0 − 3 неизвестные постоянные. Выбран полином третьего порядка, т.к. четыре неизвестные в уравнении могут быть отнесены к каждой из четырех степеней свободы узлов

элемента. Уравнение (2) может быть записано в матричной форме:

0

( ) = [1 2 3] [ 1] (3)

2

3

или

где p – вектор базисной функции и α – вектор коэффициентов. Величина поворота элемента θ может быть получена дифференцированием уравнения (2) с учетом (1).

Четыре неизвестные постоянные 0 − 3 могут быть определены из граничных условий: При = − или = −1

(−1) = 1

10