
Prezentatsia_Simonyants_Rezhim_sovmestimosti
.pdf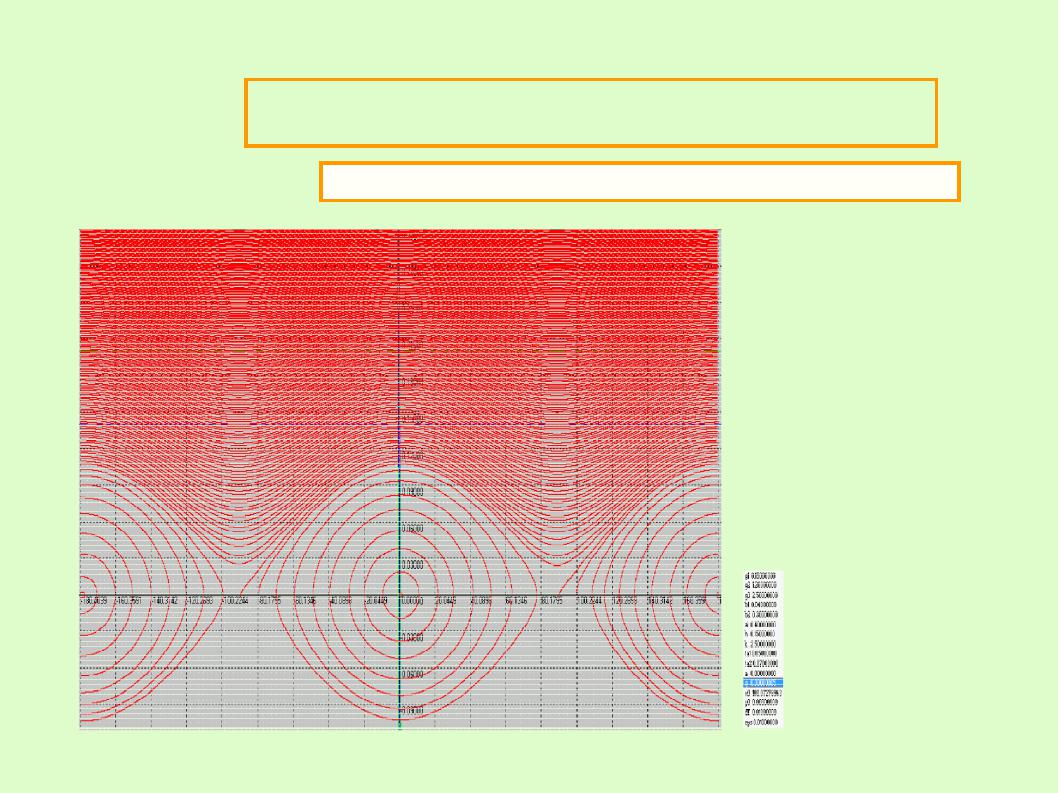
|
Фазовый портрет движений в случае диагонального тензора инерции |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 точки |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||
равновесия : |
|
|
(J |
x |
J |
y |
)sin2 0 |
|
0, |
|
2 |
|
|
, |
± π , |
|
4 |
|
|
. |
2 |
2 |
|
||||||||||||||||||
|
|
|
|
|
1 |
|
|
3 |
|
|
2 |
|
||||||||
C1 0, 1 , C3 0, 3 -устойчивые; C2 0, 2 , C4 0, 4 -неустойчивые.
c - Сепаратриса
- Область колебательныхL движений
- Область ротационныхR движений
R
|
|
c |
|
L |
L |
L |
|
|
|||
C3 |
C1 |
C3 |
|
C4 |
|||
|
C2 |
||
|
R |
|
21

1.10.2. Случай невозмущённого плоского движения по тангажу при недиагональном тензоре инерции
|
|
d2 |
3 |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||
J |
|
|
|
|
|
(J |
|
J |
|
|
)sin2 |
3 |
J |
|
cos2 0 |
|
|||
z dt |
|
|
x |
y |
yx |
|
|||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
d2 |
|
1 |
(Jx |
Jy )sin2 Jyxcos2 0 |
|||||
|
|
|
В точке равновесия : |
|
|
|
|
0 |
|
|
|||||||||
|
|
|
|
|
dt2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
Следовательно, в точке равновесия:
1 |
|
|
2Jyx |
|
|
|
(Jx Jy )sin2 Jyxcos2 tg2 |
||||
2 |
tg2 , |
где |
|||
|
|
Jx Jy |
|
|
|
главной центральной осью инерции и строительной осью. |
|
||||
Положения равновесия |
C1 0, 1 , C3 0, 3 ,C2 |
0, 2 и C4 |
0, 4 |
||
- угол между
определяются
|
2 |
|
|
|
и 4 |
3 |
|
|
2 |
2 |
|||||||
значениями: 1 , |
, 3 |
|
. |
Относительно местной вертикали колеблется ось минимального момента инерции. Поэтому фазовый портрет в плоскости ( , ) смещается
по оси 0 на угол .
22

1.10.3. Движение по тангажу при совместном действием гравитационного и постоянного моментов
Jz d22 3 2(Jx Jy )sin2 M
dt 2
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
(J |
x |
J |
y |
)sin2 M |
|
|
|
2 |
|||||||
c |
|
|
|
|
|
||||
- Сепаратриса |
|
|
|
|
|
|
|||
L |
- Область |
|
|
|
|
c |
|
||
|
колебательных |
|
|
|
|
|
|
||
|
движений |
|
|
|
|
|
|
||
R |
- Область |
|
|
|
|
|
|
||
|
ротационных |
|
|
|
|
C1 |
|
||
|
движений |
|
|
|
|
|
|||
4 точки равновесия :
C1 0, 1 , C3 0, 3 - устойчивые;
C2 0, 2 , C4 0, 4 - неустойчивые.
R
L
C2
R
23

С увеличением постоянного момента область колебательных движений сжимается
|
3 |
|
2 |
|
|
|
|
|
3 |
|
2 |
|
|
|
|
|
||
|
|
|
|
(J |
|
J |
) M, |
M |
|
(J |
|
J |
) . |
|
|
|||
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
x |
y |
|
|
|
2 |
|
|
x |
y |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C1 |
C2,C3 C4 |
|
|
M |
|
|
|
M |
|
|||||||||
1 |
, 3 |
. |
||||||||||||||||
R
c |
c |
|
C3 |
C1 |
|
L |
L |
L |
C4 |
C2 |
24

Критический случай: область колебательных движений исчезла – возможны только ротационные движения.
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(J |
|
J |
) M. |
|
C1 |
C2, C3 |
C4, |
L |
2 |
|
|
||||||||
|
x |
y |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
R
C3,C4 |
C1,C2 |
R |
|
Из любого начального положения на оси абсцисс (состояния покоя) тело переходит в ротацию.
25

1.10.4. Условия захвата градиентом гравитации
Тело захвачено градиентом гравитации, если его ось минимального момента инерции совершает лишь колебательные движения относительно местной вертикали (без ротации относительно осей 0x, 0y) .
Условие захвата. Фазовые координаты начальной точки движений по тангажу и крену должны принадлежать внутренним областям фазовых плоскостей, ограниченных сепаратрисами:
0, 0 k , |
, ; |
|
d |
|
|
dt |
|||||
|
|
|
|||
Условие захвата можно сформулировать как требование достаточной малости полной
механической энергии тела в движении относительно местной вертикали:
Eк Eп Eдоп.
Для захвата градиентом гравитации, необходимо погасить избыток кинетической энергии тела.
Если выполнены условия захвата градиентом гравитации, тело приобретает в движении по тангажу
постоянную составляющую угловой скорости, равную угловой скорости орбитального движения . При этом возникают гироскопические моменты по курсу и по крену, притягивающие ось максимального
момента инерции к бинормали.
Для того, чтобы управлять ориентацией тела захваченного гравитационном градиентом, необходимо располагать управляющим моментом, который по модулю больше суммы максимального гравитационного и максимального гироскопическогомоментов:
|
|
|
|
3 |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
M |
z |
|
|
|
(J |
x |
J |
y |
), |
M |
y |
> (J |
z |
J |
x |
) , |
M |
x |
|
2 (J |
z |
J |
y |
) |
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
26

1.11.Малые колебания под действием гравитационного момента
вокрестности устойчивого положения равновесия
- мало так, что можно
1.11.1.В плоскости тангажа свободные колебания (либрация) при условии :
|
|
J |
|
d2 |
|
3 2(J |
|
|
J |
|
) 0 |
|
d2 |
2 0 |
|
|
принять sin2 2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
z |
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
dt2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jx |
Jy |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
t Az sin zt |
z , t z |
Az cos zt z |
|
|
|
z |
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
Jz |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
0, 0 |
0 |
|
0 Az sin z, 0 |
z Az |
cos z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Tz |
|
2 |
|
|
|
Jz |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
z 0 |
|
|
|
|
|
|
|
3 Jx Jy |
||||||||||||||||||||
|
Az |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
, arctg z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
При J |
y |
J |
x |
J |
z |
|
|
T |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тело совершает незатухающие колебания, период которых соизмерим с периодом
орбитального движения.
Фазовые траектории:
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
2 |
|
|
|
А 2 |
, |
А |
|
0 |
|
||
|
|
|
|
||||||||
|
|
|
|
z |
|
z |
0 |
|
|
27 |
|
|
|
z |
|
|
|
|
|
z |
|||

1.11.2. Влияние произведений инерции (несимметричности распределения масс)
Случай плоского движения по тангажу в окрестности точки С1
|
Jz |
d 2 |
|
|
|
|
|
2 |
1 |
(J x J y )sin 2 J yxcos2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
dt |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
d 2 3 |
|
2 Jx J y |
|
|
sin 2 |
3 |
2 J yx |
cos 2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
dt2 |
|
|
|
|
J z |
|
|
|
|
J z |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Полагаем: |
sin 2 |
|
|
2 , |
cos 2 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
d 2 |
|
|
|
2 Jx J y |
|
|
|
|
2 J yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dt2 |
|
|
|
|
J z |
|
|
|
J z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J yx |
|
|
|
|
t Аz |
sin zt z |
z , |
t |
z Аz cos zt z |
|
|
z |
|
|
|
|
, |
|||||||||||||||||||||||||||||||||
|
|
|
J x |
J y |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
z |
|
|
z |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
J |
x |
J |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
z |
|
|
3 |
|
|
|
|
|
|
|
|
, Аz |
|
|
0 |
z 2 |
|
|
|
, z arctg |
|
0 |
|
|
|
||||||||||||||||||||||
|
|
|
|
J z |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||
, |
- |
угол между строительной и главной центральной осями. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Фазовые траектории: |
z |
2 |
|
|
|
|
Az |
2. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Относительно местной вертикали колеблется ось минимального момента инерции. Центральная строительная ось (связанная ось) колеблется со смещением на угол
28

1.11.3. Влияние постоянного момента МZ на движение по тангажу в окрестности точки С1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- мало так, чтоsin 2 2 |
J |
|
d2 |
3 2 |
(J |
|
J |
|
|
) M |
|
|
|
|
d2 |
|
2 |
|
Mz |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dt2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
z dt2 |
|
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
Jz |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
(Jx Jy ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
z |
|
|
|
|
|
|
M |
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
z |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
J |
z |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 2 (J |
x |
|
J |
y |
) |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jz z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
t |
|
A |
|
sin |
t |
z |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
t |
|
|
|
A cos |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
z |
z |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||
0 |
0, |
|
0 0 |
|
0 |
|
Az |
sin z , |
|
|
|
|
|
|
|
Az cos z. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
z |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Az |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
0 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
z |
arctg |
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Фазовые траектории: |
|
2 |
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительно местной вертикали колеблется ось минимального момента инерции, а центральные строительные (связанные) оси колеблются со смещением .
Это смещение - статическая ошибка , обусловленная действием постоянного момента МZ
Центробежные моменты инерции ( произведения инерции) оказывают практически такое же воздействие на тело, как и постоянный момент.
29

1.11.4. Компенсация постоянным моментом недиагональности тензора инерции
Компенсировать негативное влияние недиагональности тензора инерции (смещение z )
можно надлежащим выбором постоянного возмущающего момента. На рисунке для наглядности совмещены фазовые портреты для трёх случаев:
1)слева - колебание тела при Mz = 0,главная ось инерции которого смещена на 4о;
2)справа - колебания тела при таком значении Mz , которое в случае диагонального тензора инерции
о;
2) в центре - колебания тела, ось инерции которого смещена на 4о, но при том же значении Mz, что и во втором случае.
z |
z |
|
30
