
4Функциональные ряды
Определение 4.1. Функциональным рядом называется ряд, зависящий от параметра x R
|
∞ |
|
|
∞ |
|
|
X |
|
|
n\ |
|
|
fn(x), |
x D = D(fn). |
|||
|
n=0 |
|
|
=0 |
|
|
|
|
|
nx D : |
∞ |
Область сходимости этого ряда C = |
n=0 fn(x) сходитсяo. Íà C |
||||
|
∞ |
|
|
|
P |
|
P |
|
|
|
|
определена функция S(x) = |
fn(x), называемая суммой функционального ряда, |
||||
|
n=0 |
|
|
|
|
|
N |
|
|
|
|
|
nP |
|
|
|
|
и частичные суммы SN (x) = |
fn(x). |
|
|
|
|
|
=0 |
|
|
|
|
Определение 4.2. Ряд |
∞ |
|
|
|
|
=0 fn(x) сходится равномерно на множестве C1 C, |
|||||
åñëè |
nP |
|
|
|
|
ε > 0 M = M(ε) : N > M x C1 |SN (x) − S(x)| < ε,
C1
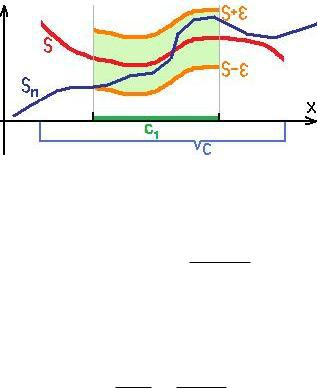
т.е. число M(ε) не зависит от точки x C1. Обозначение: SN (x) S(x). Геометрически это означает, что графики частичных сумм Sn(x), начиная с n =
M + 1, проходят через ½коридор {x C1, |y − S(x)| < ε}.
∞
Пример 4.1. Для ряда P xn имеем D = R; C = (−1; 1) : ïðè |x| ≥ 1 нарушен необхо-
|
|
n=0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
димый признак сходимости, а при |x| < 1 ряд сходится, его сумма равна S(x) = |
|
|
|
|||||||||||
|
|
|
|
|||||||||||
1 |
− |
x, |
||||||||||||
а частичные суммы SN (x) = |
1 − xN+1 |
|
|
|
|
|
|
|
||||||
ò.å. |
|
|
|
|
|
|
|
|||||||
|
нет равномерной |
|
1 |
− |
x |
|
|
|
|
|
|
|
||
(−1; 1) |
|
|
сходимости, |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε > 0 : M N > M, x C1 : |SN (x) − S(x)| ≥ ε. |
|
|
|
||||||||||
Например, для ε |
= xN+1 |
|
1/2 |
|
|
. |
p |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||||
1 возьмем любое N > M и x = |
N+1 1/2. Тогда |
|
|
|
||||||||||
S(x) − SN (x) = 1 − x ≥ 1 − 1/2 = 1
Если же взять любой меньший отрезок [−r; r] (−1; 1), то на нем ряд сходится равномерно по признаку Вейерштрасса (см. ниже).
13

Критерий Коши равномерной сходимости. Ряд íà C1, если и только если
ε > 0 K : N > M ≥ K, x C1 |
|
|
|
|
|
∞
P
fn(x) сходится равномерно
n=0
N
X
fn(x) < ε.
n=M+1
| {z }
SN (x)−SM (x)
Необходимость этого условия следует из оценки
|SN (x) − SM (x)| ≤ |SN (x) − S(x)| + |SM (x) − S(x)|,
а достаточность из оценки |SM (x) − S(x)| ≤ sup |SN (x) − SM (x)|.
N>M
Признак Вейерштрасса. Пусть существует сходящийся знакоположительный ряд |
|||||||||||
∞ |
|
C1. |
|
|
|
|
|
|
∞ |
||
P |
|
|
|
|
|
|
|
P |
|||
n=0 an (мажоранта), такой, что n |fn(x)| ≤ an |
íà C1. Тогда ряд n=0 fn(x) cходится |
||||||||||
равномерно и абсолютно на |
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Из сходимости мажоранты при всех x C1 получаем оценку |
|||||||||||
N |
|
|
|
|
N |
|
|
N |
|
|
|
|
|
|
|
n X |
|
|
X |
|
|
|
|
X |
|
|
|
≤ |
|
| ≤ |
−→ |
|
|||
|
fn(x) |
|
|
|
fn(x) |
|
an |
|
|
0, |
|
|
|
|
|
|
=M+1 |
|
|
n=M+1 |
N>M |
→∞ |
|
n=M+1 |
|
|
|
|
|
|
|
||||
∞
из которой видно по критерию Коши равномерной сходимости, что ряды P fn(x) è
n=0
∞
=0 |fn(x)| сходятся равномерно на C1. |
|
|
|
nP |
∞ |
|
|
Пример 4.1 (продолжение). Для ряда |
|
|
|
=0 xn на отрезке [−r; r], 0 < r < 1, мажорантой |
|||
является сходящийся ряд ∞ rn. |
nP |
|
|
nP |
|
|
|
=0 |
|
|
|
Пример 4.2. Доказать равномерную сходимость ряда |
∞ |
(−1)n xn на отрезке [0; 1]. |
|
|
|
X |
|
n
n=1
Доказать по признаку Вейерштрасса не получится, поскольку при x = 1 ряд сходится условно. Докажем равномерную сходимость непосредственно, пользуясь тем, что при всех x (0; 1] данный ряд является рядом Лейбница:
|
| N |
|
− |
|
|
| ≤ |
|
N+1 |
|
|
≤ |
N + 1 |
(0;1] |
|
|
→ ∞ |
|
||
|
(x) |
S(x) |
N + 1 |
xN+1 |
|
0 |
ïðè N |
. |
|||||||||||
|
S |
|
|
|
(−1) |
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
Теорема 4.1. (о непрерывности суммы). Пусть ряд |
fn(x) сходится равно- |
||||||||||||||||||
мерно на |
|
|
|
|
I R |
|
|
|
|
fn(x) |
|
|
P |
|
I. Тогда сумма |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
промежутке |
|
|
|
, и все функции |
|
|
непрерывны на |
|
|
|||||||||
ðÿäà S(x) также непрерывна на I.
14

Доказательство. Возьмем точку x I и зададим ε > 0. В силу равномерной сходимости, N: |SN (y) − S(y)| < ε/3 ïðè âñåõ y I. Частичная сумма SN непрерывна в точке x, поэтому δ > 0 : |SN (y) − SN (x)| < ε/3 y Uδ(x) ∩ I. Тогда для всех
точек y Uδ(x) ∩ I получаем оценку
|S(y) − S(x)| ≤ |S(y) − SN (y)| + |SN (y) − SN (x)| + |SN (x) − S(x)| < 3ε + 3ε + 3ε .
Следующий пример показывает, что, если ряд из непрерывных функций сходится |
||||||||||||||
неравномерно, то его сумма может оказаться разрывной. |
|
|
|
|
|
|||||||||
Пример 4.3. Рассмотрим ряд |
∞ fn(x) на отрезке [0; 1], ãäå |
|
|
|
|
|
||||||||
|
|
|
nP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
fn(x) = xn+1 − xn |
ïðè |
n = 1, 2, 3, . . . |
|
|
|
|
||||||||
|
|
|
x |
ïðè |
n = 0 |
|
|
|
|
|
|
|||
Тогда частичные суммы равны SN (x) = xN+1. На отрезке |
[0; 1] |
ряд сходится к |
||||||||||||
разрывной функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
N→∞ |
N→∞ |
|
= |
|
1 |
|
x = 1. |
|
|
||||
n=0 |
|
ïðè |
|
|
||||||||||
fn(x) = lim SN (x) = lim xN+1 |
|
0 |
ïðè |
0 |
≤ x < 1, |
|||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 4.2. (о почленном интегрировании). Пусть ряд |
∞ fn(x) сходится |
|||||||||||||
|
[ ; ] |
|
|
|
n( |
) |
|
|
|
|
|
P[ ; |
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
равномерно на отрезке |
a b , и все функции f |
|
x |
непрерывны на |
a b . Тогда сумма |
|||||||||
ряда S(x) интегрируема на [a; b], причем |
∞ Z b fn(x)dx. |
|
|
|
|
|
||||||||
|
|
Z b S(x)dx = |
|
|
|
|
(3) |
|||||||
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
n=0 a |
|
|
|
|
|
|
|
|
|
|
Доказательство. Интегрируемость S(x) следует из е непрерывности. При каждом N N из линейности интеграла следует равенство
Z b SN (x)dx = |
N Z b fn(x)dx. |
(4) |
|
X |
|
an=0 a
Будем переходить к пределу по N. Правая часть (4) имеет конечный предел при N → ∞, это проверяется по критерию Коши для числового ряда:
N |
|
b |
|
|
|
|
b |
− |
|
≤ − |
I |
| − | −→→∞ |
|
||
n=M+1 |
Z |
a |
|
Z |
a |
|
|
||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
fn(x)dx |
= |
|
|
(b |
a) sup SN SM |
|
0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N>M |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в силу равномерной сходимости. Таким образом, правая часть (4) сходится к правой части (3). Для левых частей имеем соответствующую сходимость:
|
b |
− |
Z |
b |
|
≤ − |
I |
| |
− |
| −→→∞ |
a |
a |
|||||||||
Z |
SN (x)dx |
|
S(x)dx |
|
(b |
a) sup SN (x) |
S(x) |
0. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N>M |
|
|
|
|
|
|
|
|
|
||
15

|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4.4. Ряд n=0(−1)nxn сходится равномерно на [−r; r] r < 1. Поэтому его |
||||||||||||||||||||
сумму можно |
|
P |
|
|
|
|
|
|
|
|
|
|
[0; x] èëè [x; 0] ïðè |
| |
x |
| |
< 1, |
|||
|
|
почленно интегрировать по любому отрезку |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
получится ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∞ |
1)nxn+1 |
∞ |
x |
|
x |
|
|
|
x |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(− |
|
= n=0 Z (−1)nun du = Z |
S(u)du = Z |
|
du = ln(1 + x). |
|
|
|
|||||||||||
n=0 |
n + 1 |
|
1 + u |
|
|
|
||||||||||||||
X |
|
|
|
|
X |
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
A поскольку ряд |
∞ |
(−1)nxn+1 |
|
|
|
|
|
|
[0; 1] (см. пример |
|||||||||||
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
n + 1 |
сходится равномерно на отрезке |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.2), то его сумма непрерывна на [0; 1], и равенство |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
∞ (−1)nxn+1 |
= ln(1 + x) |
|
x ( |
1; 1) |
|
|
|
|
|||||||
|
|
|
|
X |
|
|
|
|
|
|
|
− |
|
|
|
|
||||
|
|
|
|
n=0 |
n + 1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
продолжается по непрерывности и в точку x = 1. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
||
Теорема 4.3. (о почленном дифференцировании). Пусть ряд S(x) = |
|
|
fn(x) |
|||||||||||||||||
n=0
сходится на промежутке I R; все функции fn(x) имеют непрерывные производные3
íà I. Пусть ряд
∞
X
T (x) = fn0 (x)
n=0
сходится равномерно на всяком отрезке [α; β] I. Тогда сумма ряда S(x) дифференцируема на I, причем S0(x) = T (x).
Доказательство. Зафиксируем точку a I. Функция T (x) непрерывна = интегрируема на всяком отрезке в I. Тогда для каждого x I имеем
x |
∞ |
x |
∞ |
Z |
Z |
|
X |
X |
a |
T (u)du = n=0 a |
fn0 (u)du = n=0 fn(x) − fn(a) = S(x) − S(a). |
Следовательно, S(x) является первообразной для T (x) íà
Пример 4.5. Продифференцировав почленно |
∞ |
(−1)nxn |
|
получаем ряд |
X |
|
n=0 |
I.
1
= 1 + x ïðè x (−1; 1),
|
1 |
0 |
= − |
1 |
∞ |
∞ |
(−1)k(k + 1)xk |
1 + x |
(1 + x)2 |
= n=1 |
(−1)nnxn−1 = − k=0 |
||||
|
|
|
|
|
X |
X |
|
на том же интервале (−1; 1). Èòàê,
1 |
|
∞ |
|
|
|
|
Xk |
− 2x + 3x2 − 4x3 + 5x4 − 6x5 + . . . |
|
(1 + x)2 = |
||||
(−1)k(k + 1)xk = 1 |
||||
|
|
=0 |
|
|
3åñëè x левый конец I, то имеется в виду правая производная; если правый конец, то левая.
16
