§4.Линейно зависимые и линейно независимые системы векторов.

Определение 1. Система векторов {a₁,…,a_n} называетсялинейно зависимой, если найдутся коэффициентыλ₁,…,λ_nне все равные нулю, линейная комбинация с которыми равна нулю, т.е.

Определение 2. Система векторов {a₁,…,a_n} называетсялинейно независимой,если ее линейная

комбинация равна нулю толькос нулевыми коэффициентами:.

Имеют место несколько простых утверждений.

Теорема 1 (необходимое и достаточное условие линейной зависимости). Векторыа₁,…,a_n– линейно зависимыкогда хотя бы один из них является линейной комбинацией остальных.

{1.(необходимость: {a_k} – л.з. ):Пусть, для определенности,

, т.е.а₁− линейная комбинация остальных.

2.(достаточность: a_m– л.к.):система лин. зав.}

Теорема 2. Если один из векторов системы равен нулю, то вся система линейно зависима.

{0a₁+ … + 0a_n-1+}

Теорема 3.Если подсистема линейно зависима, то и вся система линейно зависима.

{}

Примеры.

1) . 2)они компланарны.

Отсюда следует, что три вектора на плоскости всегда линейно зависимы.

3) Четыре вектора в пространстве всегда линейно зависимы.

4) {f₁ = 1, f₂ = x, f₃ = x² } – линейно независимы.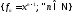

5) {sin²x,cos²x, 1} − линейно зависимы.

§5. Базис. Координаты. Размерность.

Определение 1. Базисомвекторного пространстваLназывается система элементов,

удовлетворяющая двумусловиям:

1) система {e₁,…,e_n} линейно независима.

2) Любой вектор L линейно выражается через базисные (т.е. является линейной комбинацией элементове₁,е₂, … ,е_n):.

Примеры. Базис на плоскости (V₂– 2 неколлинеарных вектора), в пространстве (V₃– 3 некомпланарных вектора), в пространстве многочленов степени ≤n : (1,х,х²,…,хⁿ).

Теорема 1. Коэффициенты разложения по базису – единственны.

{Пусть }

Определение 2. Координатами вектора в некотором базисе называются коэффициенты разложения по этому базису:а= () или.

Замечания.1. В силуТ.1 данное определение – корректно.

2. В качестве стандарта можно рассматривать как векторы – строки , так и векторы – столбцы.

3. Координаты базисных векторов е₁,е₂,е₃(в пространстве) в собственном базисе равны:

е₁= (1,0,0),е₂= (0,1,0),е₃= (0,0,1).

Определение 3. Размерностью векторного пространстваL (обозначаетсяdimL) называется максимальное число линейно независимых векторов этого пространства.

Если такого числа не существует – пространство называется бесконечномерным.

Теорема 2. Размерность линейного пространства равна числу базисных векторов. {б/д}

Отсюда, в частности, следует, что все базисы одного пространства состоят из одинакового числа векторов.

Примеры.V₂; V₃; Rⁿ; C[a,b].

Результаты линейных операций легко вычисляются в координатной форме.

Теорема 3. При сложении векторов их соответствующие координаты складываются:

.

{}

Теорема 4. При умножении вектора на число его координаты умножаются на это число:

λа = (λα₁,…,λα_n). {д – во аналогично}

В заключение рассмотрим пример базиса, который используется наиболее часто.

Определение 4. Ортонормированным базисом в пространстве называется базис, состоящий из трех взаимно ортогональных векторов единичной длины (на плоскости – из двух).

Эти векторы обозначают буквами i, j и k и называют

базисными ортами.Таким образом, выполняются соотношения

аa₃k, а произвольный вектора

ka₂jможет быть представлен в следующем виде (рис.10):

j a = a₁ i + a₂ j + a₃ k = ( a₁, a₂, a₃ ).

a₁i i

рис.10