Шпора по Начерталке №3

1 )- Одномерные тела : отрезок, линия

- Двумерные: плоская фигура отсек поверхности

- Трёхмерные : любая объёмная фигура

2 )Проецирование – это процесс, в результате которого получают изображения , являющиеся проекциями на плоскость. Аппарат проецирования включает в себя изображаемые объекты - точки , проецирующие лучи, и плоскость проекции на которой получается изображение объектов. Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до пересечения с плоскостью проекций.

4) 1.Двумя точками (А и В).

Рассмотрим две точки в пространстве А и В .Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка [AB] на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка:  [A₁B₁]<[AB]; [A₂B₂]<[AB]; [A₃B₃]<[AB].

2. Двумя плоскостями (a; b).

Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии

3. Двумя проекциями.Пусть в плоскостях П₁  и П₂ даны проекции прямых заданных отрезками [А₁В₁] и [A₂B₂]. Проведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные, линией их пересечения будет прямая заданная отрезком [АВ],проекциями которой являются отрезки [А₁В₁] и [А₂В₂].

5 )

Положение плоскости в пространстве определяется (рис.3.1): тремя точками, не лежащими на одной прямой (1), прямой и точкой, взятой вне прямой (2), двумя пересекающимися прямыми (3) , двумя параллельными прямыми (4), геометрической фигурой (5), следами плоскости (6).

6) Главные линии плоскости. К прямым, занимающим особое положение в плоскости, относят горизонтали, фронтали, профильные прямые и линии наибольшего наклона к плоскостям проекций. Эти линии называют главными линиями плоскости. Горизонталь - прямая, лежащая в плоскости и параллельная плоскости проекций П1. Фронталь - прямая, лежащая в плоскости и параллельная плоскости проекций П2. Профильные прямые - прямая, лежащая в плоскости и параллельная плоскости проекций П3. Линиями наибольшего наклона плоскости к плоскостям П1, П2, П3 называют прямые, лежащие в ней и перпендикулярные или к горизонталям плоскости, или к ее фронталям, или к ее профильным прямым. Соответственно определяется наклон плоскости к плоскостям П1, П2 или П3 Линия наибольшего наклона к плоскости П1, называется линией ската.

7 ) Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается

данная, различают: горизонтальный, фронтальный и профильный следы плоскости.Точка пересечения прямой и плоскостй проекции наз. СЛЕДОМ прямой. Существуют горизонтальные следы (если а ∩П1=Н( Н1,Н2,Н3). Фронтальные следы (если а ∩П2=F( F1,F2,F3). Профильные следы (если а ∩П3=Р( Р1,Р2,Р3)

8 ) Свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекций. Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости)

• 1. Горизонтально-проецирующая плоскость α ┴ π1. Плоскость α, перпендикулярная горизонтальной плоскости проекции π1, называется горизонтально проецирующей . Основным свойством горизонтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π1 в прямую линию (горизонтальный след плоскости h0α). Угол b, который составляет горизонтальный след плоскости h0a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций p2. Фронтальный след такой плоскости перпендикулярен оси Х (f0a ┴ X).

• 2. Фронтально-проецирующая плоскость β ┴ π2.

Плоскость b перпендикулярная фронтальной плоскости проекций π2 называется фронтально проецирующей. Основным свойством фронтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π2 в прямую линию (фронтальный след плоскости f0β). Угол a, который составляет фронтальный след плоскости f0β с координатной осью Х, равен углу наклона плоскости b к плоскости проекций π1. Горизонтальный след такой плоскости перпендикулярен оси Х.

Плоскости, параллельные плоскостям проекций

(плоскости уровня)

1. Горизонтальная плоскость γ || π1. Плоскость γ, параллельная плоскости π1, называется горизонтальной. Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскость проекций в натуральную величину (Δ А1В1С1 = ΔАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f0g | | Х).

2. Фронтальная плоскость δ | | π2. Плоскость δ, параллельная плоскости π2, называется фронтальной. Любая фигура, расположенная в такой плоскости, проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.

Горизонтальный след фронтальной плоскости параллелен оси Х.

9 ) Две прямые пространства могут иметь различное расположение . Они могут совпадать а = b, быть параллельными c|| d, пересекаться т ^ n и скрещиваться (k° / l). Если одна прямая прямого угла паралельна к плоскости проекции, а вторая сторона не перпендикулярна, то прямой угол проецируется без изкожения.

10 ) Преобразование чертежа отображает изменеие положения геометрических образов или плоскостей проекций в пространстве. Задача преобразования комплексного чертежа может быть решена перемещением проецирующего тела в пространстве до требуемого положения или изменением в пространстве положения плоскостей проекций относительно геометричекого тела. В основном используются 3 спсоба преобразования чертежа : плоскопараллельный перенос, способ вращения и способ замены плоскостей проекции. Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей. Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.

11) Так как частных положений у прямых два и у плоскости два, то существуют четыре исходные задачи для преобразования комплексного чертежа:

прямую общего положения сделать прямой уровня;

прямую уровня сделать проецирующей;

плоскость общего положения сделать проецирующей;

проецирующую плоскость сделать плоскостью уровня.

12) Этот метод заключается в том, что любая точка вращается вокруг какой-либо оси, перпендикулярной к одной из плоскостей проекции. При этом точка в пространстве движется по траектории окружности, которая лежит в плоскости, перпендикулярной к оси вращения. Система плоскостей проекций остается неизменной.

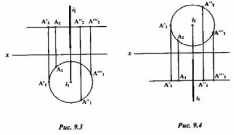
Например, при вращении точки А вокруг оси i (рис. 9.3), перпендикулярной к П2, она движется по траектории, которая проецируется на плоскость П1 в виде окружности (точки А1 A1', a1, a1'" и т.д.), а на плоскость П2 - в виде следа горизонтальной плоскости уровня. Все фронтальные проекции точки А (А2, А2', А2" и т.д.) находятся на фронтальном следе горизонтальной плоскости. Точка i1 представляет собой горизонтальную проекцию оси i, а прямая i2 — ее фронтальную проекцию.

Если вращать точку А вокруг оси i, перпендикулярной к фронтальной плоскости проекций П2 (рис. 9.4), то фронтальные проекции А2, А2', А2" и т.д. точки А будут лежать на окружности, плоскость которой перпендикулярна к оси i и горизонтальной плоскости проекции. При этом горизонтальные проекции А2 А2', А2" и т.д. точки А будут расположены на горизонтальном следе этой плоскости

13 ) Методь плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 145). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.

14)Суть метода заключается в том, что осью вращения выбирается одна из линий уровня - горизонталь или фронталь плоскости или плоской фигуры. Таким образом, плоскость как бы поворачивается вокруг некоторой оси, принадлежащей этой плоскости, до положения, при которой эта плоскость становится параллельной одной из плоскостей проекций.

15 ) Поверхностью называют множество последовательных положений линий, перемещающихся в пространстве.  в качестве образующей взята прямая 1. Закон перемещения образующей задан направляющей а и прямой b. При этом имеется в виду, что образующая 1 скользит по направляющей а, все время оставаясь параллельной прямой b.  Такой способ образования поверхностей называют кинематическим. С его помощью можно образовывать и задавать на чертеже различные поверхности. В частности, на рис.3.1 изображен самый общий случай цилиндрической поверхности.   Другим способом образования поверхности и ее изображения на чертеже является задание поверхности множеством принадлежащих ей точек или линий. При этом точки и линии выбирают так, чтобы они давали возможность с достаточной степенью точности определять форму поверхности и решать на ней различные задачи.  Для задания поверхностей выбирают такую совокупность независсимых геометрических условий , которая однозначно определяет данную поверхность в пространстве. Эту совокупность наз.определителем поверхности.. Определитель состоит из 2-х частей геометрической, и алгоритмической. В геометрическую часть определителя входят геометрические фигуры и отношения между ними. В алгоритмическую часть - закон образования поверхности. 

Понятие проекции.

Проекцией точки М на некоторой плоскости называют изображение, которое строится в нижеследующей последовательности.

Через данную точку М необходимо провести прямую, которая не параллельна данной плоскости. Точку пересечения данной прямой и плоскости назовем точкой m. Полученная точка m будет являться проекцией точки М на данную плоскость. Прямую Mm называют проектирующей прямой, а данная плоскость называется плоскостью изображения.

13 ) Поверхность вращения - поверхность , образованная направляющей L вращением вокруг оси j. При задании поверхности на ортогональном чертеже ось вращения обычно располагают перпендикулярно одной из плоскостей проекций. На рисунке ось i П1. В этом случае все параллели поверхности, горло и экватор проецируются на П1 в истинную величину, а на П2 в отрезки прямых, перпендикулярные i2 – проекции оси i. Задание поверхности осью i и образующим полумеридианом lненаглядно. Поэтому на чертеже строят проекции главного меридиана q1 и q2, проводят проекции горла, экватора и двух параллелей, образованных вращением верхней точки Аи нижней – Е.

17 ) В общем случае линия может принадлежать поверхности или не принадлежать. Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности Исключение составляет случай, когда линия представлена прямой, а поверхность — плоскостью. В этом случае для принадлежности прямой плоскости достаточно, чтобы хотя бы две точки ее принадлежали этой поверхности .Задачи построения линий, принадлежащих поверхности, входят составной частью в задачи построения линий пересечения поверхностей плоскостью и пересечения двух поверхностей, которые рассматриваются в . Если линия не принадлежит поверхности, то они пересекаются. Простейшим случаем является пересечение с поверхностью прямой линии. Задача решается путем заключения данной линии в какую-либо проецирующую плоскость и построением натуральной величины сечения, из которого легко определить точку входа и выхода прямой. Точка может принадлежать поверхности и не принадлежать. Точка принадлежит поверхности, если она лежит на линии, расположенной на этой поверхности., в точка М принадлежит сферической поверхности, так как она находится на линии окружности /г', лежащей на этой поверхности. Точки А и В тоже принадлежат сферической поверхности, так как они расположены на линиях очерковых окружностей, принадлежащих сферической поверхности. Примеры принадлежности точки поверхности можно привести и в случае наличия конической поверхности , поверхности тора и поверхности более сложной формы.

18 ) При вращении окружности вокруг прямой, лежащей в плоскости образующей окружности, образуются торовые поверхности.

1. Если R < r, то образующая окружность l не пересекает ось вращения i, поверхность называется кольцом или открытым тором.

2. Если R > либо = R, то окружность касается оси или пересекает ее, поверхность называется закрытым тором.

3. Если r = 0, то образуется сфера.

4. При вращении дуги окружности, плоскость которой может в общем случае пересекать ось вращения образуется поверхность, которая называется глобоид.

Циклические поверхности

Циклической поверхностью называется поверхность, образованная непрерывным каркасом круговых сечений. На циклической поверхности расположено, по крайней мере, одно семейство круговых образующих (постоянного или переменного радиуса). Задание циклической поверхности должно однозначно определять положение плоскости каждой окружности, положение в плоскости и величину радиуса. Циклическую поверхность можно задать плоскостью параллелизма, направляющей а и линией, которой принадлежат центры семейства окружностей Q (а, i, Г). На рисунке показана поверхность Q (а, i, Г), где плоскости окружности циклической поверхности параллельны плоскости проекций П1. Распространенные на практике разновидности циклических поверхностей - трубчатые поверхности переменного или постоянного радиуса.

19 ) Задачи, связанные с решением вопросов взаимного расположения геометрических фигур на комплексном чертеже, называются позиционными.

2 главные Позиционные задачи: задачи на взаимную принадлежность и задачи на взаимное пересечение.

1 ) Решение позиционных задач на принадлежность предполагает работу с линиями поверхности графически простыми, например прямой или окружностью. Это необходимо для того, чтобы не усложнять построений на комплексном чертеже. Для правильного выбора этих линий надо знать, какие семейства линий несет на себе та или иная поверхность.

2 ) Задачи на взаимное пересечение связаны с построением точек, принадлежащих одновременно двум рассматриваемым геометрическим образам, например прямой и плоскости, двум плоскостям, плоскости и поверхности, двум поверхностям. Каждую из этих точек строят в пересечении двух вспомогательных линий. Эти линии должны быть графически простыми и принадлежать одной вспомогательной плоскости или поверхности. Выбор вспомогательных, поверхностей (посредников), несущих в себе вспомогательные линии, зависит от формы пересекающихся поверхностей. Совокупность построенных общих точек позволяет построить линию пересечения геометрических образов.

24 ) Простейшая позиционная задача с использованием этого метода - оценка взаимного расположения прямой и плоскости. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость g и установим относительное положение двух прямых а и в, последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a (рис.1). Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости a, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю, когда прямая а пересекает плоскость a.

25 ) Основу способа вспомогательных секущих сфер составляют особенности взаимного пересечения так называемых <соосных поверхностей вращения>. К ним относятся поверхности, оси вращения которых совпадают, то есть несколько поверхностей имеют одну и туже ось вращения.

Нетрудно видеть, что две соосные поверхности пересекаются друг с другом по окружностям (рис. 23). Причем количество окружностей пересечения двух соосных поверхностей равно числу точек пересечения меридианов этих поверхностей. Действительно, если одна из поверхностей образована вращением меридиана l(l₂), а другая — меридиана D(D₂), представляющего в данном случае окружность, вокруг общей оси i(i₂), то точки A, B, C и K будут описывать окружности, общие для обеих поверхностей. При этом, если общая ось i поверхностей вращения перпендикулярна какой-либо плоскости проекций, то эти окружности проецируются на одну из них в виде отрезков, соединяющих точки пересечения меридианов и перпендикулярных оси вращения, а на другую — без искажения в окружности.

Эти особенности взаимного пересечения двух соосных поверхностей вращения, одна из которых является сферой, и составляют основу способа вспомогательных секущих сфер. Сущность применения способа вспомогательных секущих сфер для построения линии взаимного пересечения двух поверхностей вращения состоит в том, что каждая из заданных поверхностей вращения пересекается одной и той же вспомогательной сферой. При пересечении вспомогательной сферы с каждой из заданных поверхностей вращения образуются окружности. Точки пересечения полученных окружностей являются общими для обеих поверхностей вращения и поэтому принадлежат линии взаимного пересечения этих поверхностей. При этом пересекающиеся поверхности должны иметь общую плоскость симметрии, параллельную одной из плоскостей проекций. Каждая из поверхностей должна содержать семейство окружностей, по которым ее могут пересекать вспомогательные сферы, общие для обеих поверхностей.

В зависимости от расположения осей пересекающихся поверхностей вращения относительно друг друга применяются две разновидности способа вспомогательных секущих сфер. Если оси поверхностей пересекаются, то применяется способ вспомогательных концентрических секущих сфер, то есть сфер, проведенных из одного общего центра. Центром проведения таких сфер является точка пересечения осей вращения заданных поверхностей. 

Если же оси поверхностей параллельны друг другу или являются скрещивающимися, то применяется способ вспомогательных эксцентрических сфер. В этом случае вспомогательные секущие сферы проводят из разных центров. Рассмотрим особенности применения разновидностей способа вспомогательных секущих сфер для построения линии взаимного пересечения поверхностей вращения.

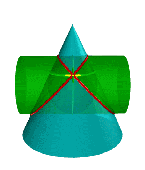
26 ) Если две поверхности второго порядка описаны около третьей поверхности или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки линий касания.

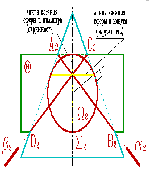
а) модель			б) эпюр
Рисунок 131. Пересечение конуса и цилиндра имеющих общую вписанную сферу

В соответствии с этой теоремой линия пересечения конуса Σ и цилиндра Q (рис.131), описанных около сферы W, будут плоскими кривыми – эллипсами (расположенными в плоскостях a и b), фронтальные проекции которых изображаются прямыми А₂В₂ и С₂Д₂,

Теорема Монжа находит эффективное применение при конструировании трубопроводов.

27 ) Метрическими называются задачи, связанные с измерением расстояний и углов. В них определяются действительные величины и форма геометрических фигур, расстояния между ними и другие характеристики по их метрически искаженным проекциям. Решение метрических задач основано на том, что геометрическая фигура, принадлежащая плоскости, параллельной плоскости проекций, проецируется на нее в конгруэнтную ей фигуру (см. аксиомы параллельного проецирования). 1 главная метрическая задача.

Определение натуральной велечины отрезка способом прямоугольного треугольника. Натуральная велечина отрезка – это гипотенуза прямоугольного треугольника , один катет которого сама проекция отрезка 2 катет равен разнице координат вершин отрезка по оси перпендикулярной к плоскости первоначального проецирования ( например по z).

2 главная метрическая задача. Определение наикратчайшего расстояния от точки дло плоскости или другого геометрического образа. Если прямая в пространстве перпендикулярна к проекции этой плоскости , то и рпоекция данной прямой перпендикулярна к проекциям следа плоскости.

28 ) А)Определение длины отрезка прямой позволяет решить задачу определения расстояния от точки до точки, так как это расстояние и определяется отрезком прямой. Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки к прямой. Отрезок этого перпендикуляра изображается в натуральную величину на плоскости в том случае, если он проведен к проецирующей прямой. Значит, нужно преобразовать чертеж данной прямой, сделав ее в новой системе плоскостей проекций проецирующей. Б)определение расстояния от точки до плоскости

Алгоритм решения. 1.Определяем расстояние от (т) В до плоскости DEFс помощью  метода рямоугольного треуг.. 2.В горизонтальной плоскости из В1 опускаем перпендикуляр на  11Е1 и получаем горизонтальную проекцию расстояния ,В121 где 21 11Е1 . 3.Строим фронтальную проекцию (т)22 и получаем  фронтальную проекцию расстояния В222 4. Из (т)В2 опускаем перпендикуляр на Е212 и получаем (т)32. 5. На горизонтальной проекции из (т)В1 опускаем перпендикуляр В131 =В232. 6. Соединив (т)31 и (т)21 получим натуральный размер расстояния от (т)В до DEF.

7. DEF расположенна от KLM на расстоянии 45мм

29 ) Расстояние от точки А поверхности Q измеряют по нормали до точки пересечения нормали с поверхностью. Найти расстояние от

точки А поверхности до поверхности сферы Алгоритм построения.

1. Провести проекции нормали n=АО(А₁ О₁; А₂ О₂).

2. Нормаль n(n₁, n₂) повернуть до фронтального положения n’(n₁’, n₂’).

3. Искомое расстояние равно êА₂’ М₂’ ê, т. к. êО₂А₂’ ê– истинная длинна нормали ОА. Аналогично находится расстояние от точки до поверхности конуса (рис. 7) Фронтальную проекцию нормали можно не проводить, достаточно провести фронтальную проекцию нормали n₂’ после ее поворота до фронтального положения n’: n’ (n₁’, n₂’), n₂ ^ l₂. Расстояние от точки до конуса равно длине проекции А₂’М₂’,  êАQ ê= êА₂’М₂’ ê. 

31) Истинная величина углов между пересекающимися прямыми с и d (рис. 143) определена следующим образом: плоскость угла повернута вокруг своей фронтали f (1, 2) до совмещения ее с фронтальной плоскостью уровня Ф (Ф1), проходящей через фронталь f 

Проекция MI совмещения вершины М угла между прямыми с и d находится на проекции Sum2 фронтально проецирующей плоскости Sum, в которой вращается точка М. Определив с помощью прямоугольного треугольника О2М2М натуральную величину радиуса вращения r и отложив ее на проекции Е2 от фронтальной проекции центра вращения, получаем изображение точки М на плоскости П2 в совмещенном с плоскостью Ф положении. Соединяя фронтальные проекции неподвижных точек 1 и 2 с построенной точкой М, получаем проекции с2 и d2, совмещенных с плоскостью Ф прямых с и d. Угол между прямыми с2 и d2 определяет натуральную величину искомого угла между пересекающимися прямыми с и d. Эта задача также может быть решена способом замены плоскостей проекций. Для этого двойной заменой плоскостей проекций нужно сделать плоскость угла плоскостью уровня, решив последовательно сначала третью исходную задачу, а затем — четвертую.

Натуральная величина угла между скрещивающимися прямыми определяется как угол между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым. Угол а между прямой l и плоскостью 6 может быть определен через дополнительный угол р между заданной прямой l и перпендикуляром п к данной плоскости, проведенной из любой точки прямой (рис. 144). Угол Р дополняет искомый угол а до 90°. Определив истинную величину угла Р путем вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром и, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла а между прямой l и плоскостью 0.