
Шпора по Начерталке №5
.doc|
1.Метод и аппарат ортогонального проецирования. Свойства ортогонального проецирование. Ортогональное проецирование это частный случай праллельного, при котором направление проецирование перпендикулярно плоскости проекций. Ортогональной проекцией точки называют основание перпендикуляра, проведенного из точки на плоскость проекции. Ортогональному проецированию присущи все свойства параллельного и центрального проецирования(цен.:проекция точки – точка; проекция прямой – прямая; если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой. Парал.: проекции параллельных прямых параллельны между собой; отношение отрезков прямой равно отношению их проекций;отношение отрезков двух параллельных прямых равно отношению их проекций.) При этом ортогональное проецирование имеет следующее свойство: ортогональные проекции двух взаимно перпендикулярных прямых, одна из которых параллельна плоскости проекций, а другая не перпендикулярна ей, взаимно перпендикулярны. Изложенный Монжем метод - метод ортогонального проецирования, причем берутся две проекции на две взаимно перпендикулярные плоскости проекций, - обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей
|
2
В Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов - октантов. Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают, как показано на рисунке 2.4, до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают. Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата). Если точка принадлежит хотя бы одной плоскости проекций, она занимает частное положение относительно плоскостей проекций. Если точка не принадлежит ни одной из плоскостей проекций, она занимает общее положение. При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. На рисунке 2.1. показана точка А и ее ортогональные проекции А1 и А 2. Точку А1 называют горизонтальной проекцией точки А, точка А2 - ее фронтальной проекцией. Проекции точки всегда расположены на прямых, перпендикулярных оси x21 и пересекающих эту ось в одной и той же точке А x. Справедливо и обратное, т. е. Если на плоскостях проекций даны точки А1 и А2 расположенные на прямых, пересекающих ось x21 в точке Аx под прямым углом, то они являются проекцией некоторой точки А. На эпюре Монжа проекции А1 и А2 окажутся расположенными на одном перпендикуляре к оси x21. При этом расстояние А1Аx -от горизонтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П2, а расстояние А2Аx - от фронтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П1. Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи. |
3 В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения. 2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными илифронталями.
2
3 3.1. Фронтально проецирующая
Профильно проецирующая
|
4.Задание плоскости на к.ч. плоскости частного положения: уровня и проецирующие. Их задание на к.ч. Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости:Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;Плоскость есть множество точек, равноотстоящих от двух заданных точек. Плоскость в линейной алгебре - поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением 1-ой степени. Положение плоскости в пространстве можно определить:
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный aП1; - фронтальный aП2; - профильный aП3). Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.5.5). 2.Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают: 2.1. Плоскость перпендикулярная горизонтальной плоскости проекций (^aP1), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом. 2.2. Плоскость перпендикулярная фронтальной плоскости проекций (a^П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом aП2. Плоскость перпендикулярная профильной плоскости ( ^aП3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость. 3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают: 3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (a//П1) - (^aП2,^aП3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости aП2 и aП3. Фронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (a//П2), (a^П1, a^П3). Любая фигура в этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямые - следы плоскости aП1 и aП3. 3.3. Профильная плоскость - плоскость параллельная профильной плоскости проекций (a//П3), (a^П1, a^П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости aП1 и aП2. |
5. Принадлежность точки – прямой, прямой-плоскости, точки-плоскости. Конкурирующие точки, их использование для определение видимости на к.ч. Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 3.14 точек, только одна точка С лежит на прямой АВ. В тех случаях когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П1, П2 и П3), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П1, П2 или П3. Например, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости проекций. Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость g и установим относительное положение двух прямых а и в, последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a. Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости a, параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямая а пересекает плоскость a. Таким образом возможны три случая относительного расположения прямой и плоскости:
Рассмотрим каждый случай. Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости. Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости. Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет. Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну. Рассмотрим пример (рис.5.23): Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(a//b).
|
||||
|
6. Теорема о проецировании прямого угла. Перпендикуляр к плоскости, плоскость перпендикулярна заданной плоскости. Угол - геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Углом между прямыми называется меньший из двух углов между лучами, параллельными этим прямым. Углом между плоскостью и не перпендикулярной ей прямой называется угол между прямой и её проекцией на данную плоскость. Рассмотрим ряд свойств ортогональных проекций плоских углов: 1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла). Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей. Согласно признаку перепен. Прямой и плоскости: прямая перепенд. Плосксти, если она перпен. Двум пересекающим прямым этой плоскости.
|
7. Линия наибольшего наклона плоскости общего положения к горизонтальной, фронтальной и профильной пл. проекции. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций. Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее. Линия ската всегда перпендикулярна к горизонтали данной плоскости. Линия наибольшего наклона к П2 произвольной плоскости всегда перпен. Фронтали данной плоскости. Угол между линией ската и плоскостью П1 это угол наклона на которой лежит линия ската к П1. линия наибольшего наклона П3 всегда перпен. К профильной прямой данной плоскости.Если одна из сторон. П1-горизонталь, П2-фронталь, П3- профильная. Сохраниться прямой угол
|
8. паралелльность на к.ч. 2-х прямых, прямой и плоскости, 2-х плоскостей. Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек. Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций. При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскостии не принадлежит этой плоскости. Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab. |
19. Технический рисунок, собственная и падающая тень, лучевой треугольник. Правило пограничного контраста. Технический рисунок – какая-либо проведенная аксонометрия + собственная+падующая тень, для увеличение наглядности. Для граненых поверхностей собственная тень (-это тень на поверхности объекта)распределяется согласно правило пограничного пространства (-тень затейной грани высветляется в сторону границы менее освещенной гранью). Для задание направление луча света испол. так называемый лучевой треугольник. Лучевой треуг. Задается произвольно, но из расчета чтобы полученная тень усиливала объем. Тень можно наносить штриховкой, шрафировкой и размывка. Падающая тень как правило строиться на плоскости где соит объект. Особенности: четкий контур, осветляется по мере удаления от объекта, более контрастная чем собственная. Собственная тень криволинейных поверхностей. Для нее выделяется: блик – это зона тени на пов. Объекта наиболее освященная; светотень – некоторое увеличение затемнености по мере удаление от зоны блика; граница светотени-зона на поверхности предмета где лучи проходит по касательной к ней (к ней затемненная); рефлекс- зона на пов. Объекта куда не попадает лучи света, но она высветляется по сравнению границей светотени из-за отраженного цвета от поверх. На которой стоит объект. Плоскость аксонометрия луча света перпендик. Зона блика. |
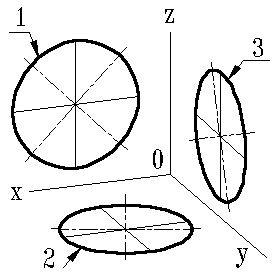
18. ортогональная аксонометрия. Показатели искажения. Основное соотношение аксонометрии. Точная и привиденная изометрия и диметрия. Соотношение осей эллипсов, сопряженные диаметры. Аксонометрическое изображение получается на базе ортогонального проекции при проецировании пространственной системы координат. Аксонометрические изображения широко применяются благодаря хорошей наглядности и простоте построений. Слово «аксонометрия» в переводе с греческого означает измерение по осям. Аксонометрический метод может сочетаться и с параллельным, и с центральным проецированием при условии, что предмет проецируется вместе с координатной системой. Сущность метода параллельного аксонометрического проецирования заключается в том, что предмет относят к некоторой системе координат и затем проецируют параллельными лучами на плоскость вместе с координатной системой. Искажение отрезков осей координат при их проецировании на П' характеризуется так называемым коэффициентом искажения. Коэффициентом искажения называется отношение длинны проекции отрезка оси на картине к его истинной длине. Так по оси x* коэффициент искажения составляет u=0*x*/0x, а по оси y* и z* соответственно υ=0*y*/0y и ω=0*z*/0z. В зависимости от отношения коэффициентов искажения аксонометрические проекции могут быть: Изометрическими, если коэффициенты искажения по всем трем осям равны между собой; в этом случае u=υ=ω; Диметрическими, если коэффициенты искажения по двум любым осям равны между собой, а по третьей – отличается от первых двух; Триметрическими, если все три коэффициента искажения по осям различны. Аксонометрические проекции различаются также и по тому углу φ, который образуется проецирующим лучом с плоскостью проекций. Если φ≠ 90o, то аксонометрическая проекция называется косоугольной, а если φ= 90o – прямоугольной. Согласно ГОСТ 2.317-69, из прямоугольных аксонометрических проекций рекомендуется применять прямоугольные изометрию и диметрию. Основное соотношение. Между коэффициентами искажения и углом φ, образованным направлением проецирования и картинной плоскостью, существует следующая зависимость: u2+υ2+ω2=2+ctq2φ, если φ=90o, то u2+υ2+ω2=2, В изометрии u=υ=ω и, следовательно, 3u2=2, откуда u=Ö2/3 ≈ 0,82. Таким образом, в прямоугольной изометрии размеры предмета по всем трем измерениям u=v=w=0,82. что соответствует увеличению изображения против оригинала в 1,22 раза. При построении прямоугольной диметрической проекции сокращение длин по оси y' (рис.9.3) принимают вдвое больше, чем по двум другим, т.е. полагают, что u=ω, а υ=0,5u. Тогда 2u2+(0,5u)2=2, откуда u2=8/9 и u≈0,94, а υ=0,47. В практических построениях от таких дробных коэффициентов обычно отказываются, вводя масштаб увеличения, определяемый соотношением 1/0,94=1,06, и тогда коэффициенты искажения по осям x' и z' равны единице, а по оси y' вдвое меньше υ=0,5. Из косоугольных аксонометрических проекций ГОСТом предусмотрено применение фронтальной и горизонтальной изометрии и фронтальной диметрии (последнюю ещё называют кабинетной проекцией).
Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось -0.71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось ось эллипсов 1, 2, 3 равна диаметру окружности, а малая - 0.58 диаметра окружности. Если димметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0.95, эллипсов 2 и 3 - 0.35 диаметра окружности. Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0.9, эллипсов 2 и 3 - 0,33 диаметра окружности. 1-эллипс (большая ось расположена под углом 900 к оси y); 2-эллипс (большая ось расположена под углом 900 к оси z); 3-эллипс (большая ось расположена под углом 900 к оси x).
|
||||
|
9. пересечение прямой и плоскости, 2-х плоскостей. Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.Две плоскости взаимно перпенд., если одна из них проходит через перпенд. К другой. Согласно признаку перепен. Прямой и плоскости: прямая перепенд. Плосксти, если она перпен. Двум пересекающим прямым этой плоскости. |
10. Метод преобразования К.Ч. – метод вращения вокруг проецирующей прямой(оси). Общий случай подобной задачи, когда требуется найти расстояние от точки до прямой общего положения, то даже построение проекции искомого отрезка без преобразования проекций не представляется возможным. Сопоставление приведенных чертежей показывает, что трудности решения одной и той же задачи существенно зависят от положения геометрических объектов относительно плоскостей проекций. В связи с этим, естественно, возникает вопрос, каким путем можно получить удобные проекции для решения поставленной задачи по заданным неудобным ортогональным проекциям. Переход от общего положения геометрической фигуры к частному можно осуществлять за счет изменения взаимного положения проецируемой фигуры и плоскостей проекций. При ортогональном проецировании это достигается двумя путями: 1. Перемещение в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве - метод плоскопараллельного перемещения. 2. Перемещением плоскостей проекций в новое положение по отношению, к которому проецируемая фигура (которая не меняет положения в пространстве) окажется в частном положении - метод замены плоскостей проекций.
|
11. Кинематический способ образовании поверхностей. Образующая и направляющая. Каркас, очерк и определитель. В начерт. Геом. Поверхности опред. Как совокупность поседовательных положений линий движущих в пространстве по опред. Закону. При задании поверхности в начерт. Геом. Исходят из кинематического способа. Поверхность нужно задать очерком. Каркас совокупность точек и линий принадлежавших данной поверхности. Поверхности могут быть закономерными и незакономерными. Начерт. Геом. Изучает закономерные поверхности. Чаще всего поверхности закономерные в начер. Геом. Задаются определителем. Определитель – минимальное, но достаточная информация для изображения поверхности на чертеже. Опред. Состоит из двух частей геометрической и алгоритмической. Поле обозначения поверхности геометрическая часть записывается которая содержит обозначение геом. Объеков, которые изображается на чертеже и однозначно задают поверхность. В квадратныъх скобках пишется все то что вы считаете нужным для расшифровки поверхности. Одну и тому поверхность можно задать с разными законами движения в пространстве. Исходя из кинематического образования поверхности дадим определение: образующая-это линия которая при свеем движении образует поверхность. Направляющая-это линия задающая закон перемещение образующей в пространстве. Образующая при своем движении всегда должна пересекать линию направляющую, тогда закон действует. В общем случае направляющих три.
|
12. Поверхности вращения. Меридианы, параллели, экватор, горло, главный меридиан. Однополостный гиперболоид. Точка на поверхности(построение 2-й проекции), построение главного полумеридиана. Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i. Геометрическая часть определителя состоит из двух линий: образующей m и оси i. Алгоритмическая часть включает две операции: 1. На образующей m выделяют ряд точек A, B, C, …F; 2. Каждую точку вращают вокруг оси i. Так создается каркас поверхности, состоящей из множества окружностей, плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором. Из закона образования поверхности вращения вытекают два основных свойства: 1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели. 2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам.
П
|
13. линейчатые поверхности. Коническая, цилиндрическая, торсовая поверхность на к.ч. Поверхность косого клина. Поверхности Каталана. Точкаа поверхности. По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая. Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся. Линейчатые поверхности с плоскостью параллелизма (поверхности каталана). Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих), параллельных некоторой плоскости α (плоскости параллелизма) и пересекающих две данные направляющие m, n (рис. 8.13). В зависимости от формы направляющих образуются три частных вида поверхностей. Цилиндроид. Цилиндроидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим кривым линиям, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.8.13). Коноид. Коноидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим, одна из которых кривая линия, а другая прямая, при этом образующая во всех положениях параллельна плоскости параллелизма. Торсовая поверхности. Если образующая окружность при образовании поверхности вокруг диаметра(сферы). Если ось вращения смещена то плоскость окружности в сторону диаметра то может образоваться закрытый или открытый тор. А если оь вращения явл. Хордой то получается закрытый тор. Гиперболический параболоид. Гиперболическим параболоидом или косой плоскостью называется поверхность, образованная движением прямолинейной образующей, параллельной плоскости параллелизма, по двум направляющим линиям – скрещивающимся прямым |
||||
|
14. Поверхности образованные вращением окружности (сфера,, тор) Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими: Сфера – образуется вращением окружности вокруг её диаметра При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг большой оси то эллипсоид называется вытянутым если вокруг малой – сжатым или сфероидом Тор – поверхность тора формируется при вращении окружности вокруг оси, не проходящей через центр окружности
|
15. Сечение прямого кругового конуса. В зависимости от положения секущей плоскости линиями сечения конической поверхности могут быть: эллипс, парабола, гипербола, а в частных случаях: окружность, прямая, две пересекающиеся прямые и точка. Если плоскость Ф пересекает все образующие поверхности конуса вращения, т.е. если φ>α, то линией сечения является эллипс В этом случае секущая плоскость не параллельна ни одной из образующих поверхности конуса. В частном случае (φ=900) такая плоскость пересекает поверхность конуса по окружности ; и сечение вырождается в точку, если плоскость проходит через вершину конуса. Е |
16. Частные случаи пересечение поверхностей 2-ого порядка. Три теоремы о распадении. Пересечение поверхностей проецирующей плоскостью. Поверхностью второго порядка называется множество точек пространства, декартовы координаты, которых удовлетворяют алгебраическому уравнению второй степени. Две поверхности второго порядка в общем случае пересекаются по пространственной линии четвертого порядка, которую называют биквадратной кривой. В некоторых случаях биквадратная кривая распадается на две плоские кривые второго порядка, причем одна из них может быть мнимой. Опуская доказательства, приведем некоторые теоремы и примеры, иллюстрирующие их применение. Три теоремы о распадении. Теорема 1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются. Теорема 2.(о двойном касании). Если две поверхности второго порядка имеют касание в двух точках А и В, то линия их пересечения распадается на две плоские кривые второго порядка, плоскость которых проходит через отрезок АВ, соединяющий точки касания. Теорема 3. (теорема Г. Монжа). Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки линий касания. Пересечение поверхностей проецирующей плоскостью. Для поиска результата пересечения объектов(прямая-поверхность точка, кривая-поверхность точка, плоскость-поверхность-плоская линия, две поверхности –кривая). Необ. Испол. посредники могут вступать проецирующие плоскости (семейство плоскостей), проецирующий цилиндр, поверхность, сферы концерические, семейство сфер экцетрические. Посредники выбираются таким образом чтобы рассекая обе заданные поверхности в результате получались на каждой из них простые в геометрическом смысле линии (это прямая или окружность, которые же надо строить по точкам). В качестве посредника подходит семейство горизонтальных плоскостей. Опред. Зона существование посредника. Определяем опорные точки, точки которые находятся без испол. посредников. При необходимости опред точки перемены видимости.
|
17. Развертки точные, приближенные и условные. Приближенная развертка наклонного конуса. Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга). Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой. Развертка будущая свернута по цил. Закону образует заданную поверхность. Развертки бывают точные приближенные и условные. И у поверхности одинаковой кривизной-конус и цилиндр.Для получение приближенной развертки в заданную криволинейную поверхность вписывается гранная поверхность с точностью. Условные развертки – имеют поверхности двойной кривизной, их нельзя без разрыва совместить с плоскостью. Развертка конической поверхности выполняется аналогично развертке пирамиды, предварительно вписав в конус n-угольную пирамиду. Если задана поверхность прямого конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ=360о r / l, где r – радиус окружности основания конуса.
|
|

 .Переход
от трех ортогональных плоскостей в
пространстве к плоскому трех картинному
чертежу. Октанты. Задание точки К.Ч.
.Переход
от трех ортогональных плоскостей в
пространстве к плоскому трех картинному
чертежу. Октанты. Задание точки К.Ч.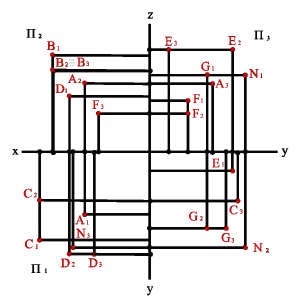 практике изображения различных
геометрических объектов, чтобы сделать
проекционный чертеж более ясным,
возникает необходимость использовать
третью – профильную плоскость проекций
П3,
расположенную
перпендикулярно к
П1
и П2.
В соответствии с ГОСТ 2.305-68 плоскости
проекций П1
П2
и П3
относятся к основным плоскостям
проекций. Модель трех плоскостей
проекций показана на рисунке 2.3. Третья
плоскость, перпендикулярная и П1,
и П2,
обозначается
буквой П3
и называется профильной. Проекции
точек на эту плоскость обозначаются
заглавными буквами или цифрами с
индексом 3.
практике изображения различных
геометрических объектов, чтобы сделать
проекционный чертеж более ясным,
возникает необходимость использовать
третью – профильную плоскость проекций
П3,
расположенную
перпендикулярно к
П1
и П2.
В соответствии с ГОСТ 2.305-68 плоскости
проекций П1
П2
и П3
относятся к основным плоскостям
проекций. Модель трех плоскостей
проекций показана на рисунке 2.3. Третья
плоскость, перпендикулярная и П1,
и П2,
обозначается
буквой П3
и называется профильной. Проекции
точек на эту плоскость обозначаются
заглавными буквами или цифрами с
индексом 3.
 .Прямая
общего положения на к.ч. Прямые частного
положения: h,f,p(уровня),
проецирующие прямые.
.Прямая
общего положения на к.ч. Прямые частного
положения: h,f,p(уровня),
проецирующие прямые.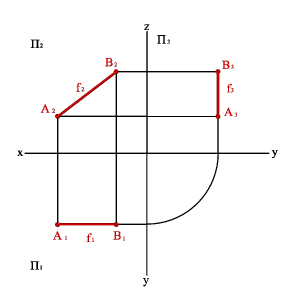 .1.
Прямые параллельные горизонтальной
плоскости проекций называются
горизонтальными
или горизонталями
.1.
Прямые параллельные горизонтальной
плоскости проекций называются
горизонтальными
или горизонталями .3.
Прямые параллельные профильной
плоскости проекций называются
профильными
.3.
Прямые параллельные профильной
плоскости проекций называются
профильными .
Прямые перпендикулярные плоскостям
проекций, называются проецирующими.
Прямая перпендикулярная одной плоскости
проекций, параллельна двум другим. В
зависимости от того, какой плоскости
проекций перпендикулярна исследуемая
прямая, различают:
.
Прямые перпендикулярные плоскостям
проекций, называются проецирующими.
Прямая перпендикулярная одной плоскости
проекций, параллельна двум другим. В
зависимости от того, какой плоскости
проекций перпендикулярна исследуемая
прямая, различают:
 Горизонтально
проецирующая
Горизонтально
проецирующая

 лоскость
проходящая через ось параллельно
фронтальной плоскости проекций
называется плоскостью
главного меридиана,
а линия, полученная в сечении, – главным
меридианом.
Гиперболоид вращения
– различают
одно и двух полостной гиперболоиды
вращения. Первый получается при
вращении вокруг мнимой оси, а второй
– вращением гиперболы вокруг
действительной оси.
лоскость
проходящая через ось параллельно
фронтальной плоскости проекций
называется плоскостью
главного меридиана,
а линия, полученная в сечении, – главным
меридианом.
Гиперболоид вращения
– различают
одно и двух полостной гиперболоиды
вращения. Первый получается при
вращении вокруг мнимой оси, а второй
– вращением гиперболы вокруг
действительной оси. сли
плоскость Ф
параллельна одной образующей поверхности
конуса, т.е. φ=α,
то линией пересечения является
парабола.
В частном случае (плоскость является
касательной к поверхности конуса)
сечение вырождается в прямую
Если плоскость Ф
параллельна двум образующим поверхности
конуса (в частном случае параллельна
оси конуса), т.е. φ<α,
то линией сечения является гипербола.
В случае прохождения плоскости через
вершину конической поверхности фигурой
сечения могут быть сами образующие,
т.е. гипербола вырождается в две
пересекающие прямые
сли
плоскость Ф
параллельна одной образующей поверхности
конуса, т.е. φ=α,
то линией пересечения является
парабола.
В частном случае (плоскость является
касательной к поверхности конуса)
сечение вырождается в прямую
Если плоскость Ф
параллельна двум образующим поверхности
конуса (в частном случае параллельна
оси конуса), т.е. φ<α,
то линией сечения является гипербола.
В случае прохождения плоскости через
вершину конической поверхности фигурой
сечения могут быть сами образующие,
т.е. гипербола вырождается в две
пересекающие прямые