3.Метод фазового пространства исследования нелинейных систем.

Фазовым пространством называется пространство координат вектора состояния X=(x₁,x₂,…,x_n) нелинейной системы, описываемой дифференциальным уравнением вида , (19.1) гдеX вообще говоря, нелинейная вектор-функция.

Решения уравнения (19.1) в фазовом пространстве изображаются фазовыми траекториями. Точки пространства, через которые проходит единственная траектория, называются обыкновенными. В противном случае точки называются особыми.

Если нелинейную функцию в правой части уравнения (19.1) аппроксимировать кусочно-линейной зависимостью, то в фазовом пространстве выделятся области, в каждой из которых будет справедливо некоторое линейное дифференциальное уравнение. Интегрирование такого уравнения всегда возможно в аналитической форме. Геометрическим образом полученного решения будет соответствующая фазовая траектория, непрерывно переходящая в соседние области. Построение фазовых траекторий и составляет существо метода фазового пространства.

В практике исследования нелинейных систем обычно ограничиваются случаем вектора состояния с двумя компонентами, что соответствует системе второго порядка, будем записывать уравнения вида (19.1) в виде двух равенств

(19.2)

При кусочно-линейной аппроксимации каждая из функций раскладывается в ряд по степеням приращений фазовых координат в окрестности точки (x₁₀ , x₂₀) . Без ограничения общности можно положить x₁₀=x₂₀=0 (в противном случае можно преобразовать переменные путем переноса начала координат). Опуская очевидные преобразования и ограничиваясь линейными слагаемыми, перейдем от (19.2) к линеаризованным уравнениям

(19.3)

Здесь коэффициенты a_{i j} (i,j =1,2) представляют собой соответствующие частные производные по фазовым координатам. Из них можно составить матрицу с собственными числами – корнями характеристического уравнения .

В матричной форме уравнение (19.3) имеет вид.(19.4)

Введем линейное преобразование переменных , после чего уравнение (19.4) примет видили после умножения слева на.(19.5)

Так как при линейном преобразовании собственные числа матриц не изменяются, то матрицу T ^–1 можно подобрать таким образом, чтобы произведение имело либо диагональную форму, либо приводилось к жордановой клетке второго порядка (случай кратных корней характеристического уравнения).

Итак, пусть .

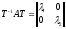В таком случае система (19.5) в скалярном виде состоит из двух дифференциальных уравнений простейшего вида (19.6)

Решение системы (19.6) очевидно 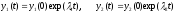.(19.7)

Соотношения (19.7) задают фазовую траекторию в параметрической форме. При непрерывном изменении параметра t изображающая точка

перемещается вдоль фазовой траектории. Эти формулы наиболее удобны для построения фазовых траекторий. Для качественного исследования возможных видов фазовых траекторий в окрестности начала координат лучше сразу исключить время, поделив уравнения (19.6). Таким образом, . (19.8)

Форма (19.8) позволяет приступить к качественному анализу поведения фазовых траекторий в окрестности начала координат. При этом могут быть следующие случаи.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3