1.Примеры элементов с нелинейными характеристиками.

1.Характеристика с насыщением (рис.18.1)

2.Дискриминационная характеристика (рис.18.2).

Характеристики такого типа встречаются в частотных дискриминаторах, а также в системах сопровождения движущихся объектов. В технической литературе их часто называют «финитными» - в связи с ограниченностью диапазона входной величины, в котором характеристика отлична от нуля.

3.Квадратичный детектор (рис.18.3)

Детектирование сигнала осуществляется для выделения огибающей,которой модулирована несущая частота. Оно встречается во всех радиоприемных устройствах, а также в устройствах сопровождения (в головках самонаведения ракет, в наземных станциях и т.п.). В случае одночастотной модуляции сигнала с несущей частотой _c входной сигнал имеет вид . (18.1)

После прохождения квадратичного детектора выходной сигнал записывается как

.

Нетрудно видеть, что после раскрытия скобок только одно слагаемое будет содержать гармонику с частотой огибающей _. После прохождения полосового фильтра амплитуда полезного сигнала определяется коэффициентом модуляции m.

Аналогичную функцию выполняет так называемый «линейный детектор» с характеристикой вида .

При (условие отсутствия «перемодуляции») в выражении (18.1) знак «модуля» распространяется только на последний сомножитель, который в этом случае имеет разложение вида.

После перемножения вновь получается только одно слагаемое с частотой огибающей. При «двухполупериодном» детектировании характеристика такого детектора имеет вид, изображенный на рис.18.4.

2.Псевдолинейная коррекция частотных характеристик.

Скачкообразное изменение параметров используется также для псевдолинейной коррекции частотных характеристик фильтров. Мы ограничимся здесь следующим примером. Поставим задачу расширения полосы пропускания апериодического элемента, описываемого линейным дифференциальным уравнением .

При установившийся процесс на выходе будет иметь вид, где.

Реализуем схему, преобразующую выходной сигнал по закону

Рис.31.3.Псевдолинейная коррекция апериодического элемента.

Из рис.31.3 видно, что фазовый сдвиг сигнала u(t) будет меньше, чем сдвиг сигнала y(t) на этой же частоте входного сигнала. Остается получить математическую оценку сдвига. Для этого найдем первые четную и нечетную гармоники сигнала u(t).

.

Аналогичная выкладка с четной гармоникой приводит к результату

.

Таким образом, первая гармоника сигнала u(t)

.

Соответственно тангенс угла сдвига по фазе

.

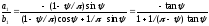Видно, что сдвиг по фазе уменьшился и это уменьшение растет вместе с частотой входного сигнала. При этом, конечно, падает и амплитуда на выходе. Этот нежелательный эффект можно скомпенсировать дополнительным усилением. Предельное значение выигрыша по сдвигу наступает при фи=пи/2. Оно равно .

3.Преобразоание уравнения высокого порядка, описывающего линейную систему управления к нормальной системе в форме Коши.

Условимся совокупность выходных координат обозначать вектором-столбцом (на письме удобно воспользоваться транспонированием строки)

Уравнения, описывающие систему управления, запишем в нормальной форме (в форме Коши)

. (4.4)

При линеаризации этих уравнений введем обозначения . . .,.

Вводя также вектор управлений ,

можно переписать систему (4.4) в матричной форме , (4.5)

где ,.

Вектор называетсявектором состояния системы.

Уравнение вида (4.5) наиболее часто используется в теоретических исследованиях в современной научной литературе. При практических вычислениях неизбежно приходится возвращаться к скалярной записи вида (4.4) или к ее линеаризованной форме.

Покажем теперь, что матричная форма записи дифференциаль-ного уравнения может быть получена непосредственно из уравнения вида (1.1), которое мы использовали для вывода частотного оператора и передаточной функции. Для этого введем обозначения

(4.6)

. . . . . .

,

Обозначения (4.6) следует рассматривать как совокупность дифференциальных уравнений. Далее без потери общности введем для краткости обозначения для коэффициентов

.

Последнее уравнение, дополняющее (4.6) до системы запишется в виде

. (4.7)

Уравнения (4.6) и (4.7) образуют систему, которую можно записать в матричной форме (4.5), где матрица

.

Нетрудно убедиться, что матрица

,

состоящая из строк истолбца после умножения на вектор

образует также вектор-столбец, и вся совокупность уравнений (4.6) и (4.7) приобретает вид

,

который с точностью до обозначения управляющего воздействия совпадает с (4.5).