1.Доказать критерий устойчивости Найквиста.

Критерий Найквиста пользуется наибольшим распространением в связи с удобством его практического применения, в частности, в логарифмических координатах. Кроме того, он особенно удобен в связи с тем, что требует построения характеристик лишь разомкнутой системы, Эта операция либо обходится минимальными вычислениями, либо вообще без них.

Для вывода критерия Найквиста рассмотрим выражение (6.2) передаточной функции замкнутой системы, полученное нами в шестой лекции. Как уже было установлено, передаточная функция линейной динамической системы представляет собой отношение двух целых полиномов, т.е. .

Подставив это выражение в (6.2), получаем .

Из последней формулы видно, что ее знаменатель представляет собой характеристический полином замкнутой системы. В то же время, обратившись к выражению ,мы замечаем, что приращение аргумента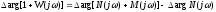(8.3)

Здесь полином N(s) следует рассматривать как характеристический полином разомкнутой системы. При доказательстве критерия Михайлова мы видели, что приращение аргумента первого слагаемого в (8.3) равно . Допуская существованиеm корней с положительной вещественной частью у полинома N(s), подсчитаем приращение аргумента согласно (8.3)

. (8.4)

Геометрически это означает, что годограф левой части в случае устойчивости замкнутой системы должен охватывать начало координат m/2 раз. Кроме того, этот годограф отличается от годографа разомкнутой системы простым сдвигом вдоль вещественной оси на единицу. Ввиду последнего замечания критерий Найквиста формулируется следующим образом: для того, чтобы замкнутая автоматическая система была устойчива, необходимо, чтобы годограф ее передаточной функции в разомкнутом состоянии охватывал точку (-1, j*0) m/2 раз, где m - число корней с положительной вещественной частью характеристического полинома разомкнутой системы.

2.Наблюдаемость динамических систем. Теорема Калмана о наблюдаемости.

Система называется полностью наблюдаемой, если по измеренным значениям компонент вектора Y при заданном управлении G ( t ) ( 0 < t <T ) можно определить начальное значение вектора состояния X

Если путем измерения вектора Y восстанавливаются начальные значения не всех компонент вектора X, то система будет не полностью наблюдаемой, в частности, система может оказаться полностью ненаблюдаемой.

Справедлива следующая теорема Калмана. Система будет полностью наблюдаемой, если ранг матрицы равенn.

Пример. Система описывается уравнениями

Вектор измерений представляет собой скалярную величину Y = x_1.

Составим матрицы, указанные в теореме.

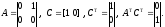
Следовательно, матрица Калмана в данном случае имеет ранг, равный двум. Система наблюдаема.

Пример 15.3.

Пусть для системы из предыдущего примера вектор наблюдений также выродился в скалярную величину, но на этот раз Y = x₂ . В этом случаеКак видим, ранг матрицы Калмана на этот раз равен единице, в то время как порядок системы равен двум. Следовательно, система не полностью наблюдаема. В самом деле, по измерениям первой производной функцииx₁( t ) нельзя установить, чему равна эта функция при t = 0, т.к. одной и той же производной соответствует бесчисленное множество первообразных.