2.Алгоритм поиска минимума интегральной оценки в пространстве параметров.

Уменьшение оценки будем осуществлять подбором параметров tau И teta корректирующего элемента. Исходя из их допустимых значений, которые определяются рис.12.5, построим начальный симплекс с вершинами в точках с координатами, задаваемыми

№точки	tau	teta	Интегр.оценка
1	0.230	0.350	3.7203
2	0.220	1.150	1.6862
3	0.086	0.710	0.1664

Из таблицы видно, что наибольшее значение интегральной оценки соответствует параметрам первой точки. Из этой точки делается пробный шаг в новую точку с координатами, вычисляемыми по формулам

В результате подсчета получаем новое значение интегральной оценки (Табл.13.2)

№ точки			Интегр.оценка
2	0.220	1.150	1.6862
3	0.086	0.710	0.1664
4	0.076	1.510	0.6629

Пробный шаг привел к уменьшению интегральной оценки и поэтому принимается. Нетрудно видеть, что геометрически этот шаг соответствует построению отрезка, проведенного из вершины с наибольшей интегральной оценкой через середину противоположной стороны треугольника-симплекса, образованного тремя первоначально выбранными точками. Во вновь образованной таблице «конкурирующими» вершинами оказались две прежних и одна новая. Однако повторение операции с пробным шагом не приведет к положительному результату, ибо новая вершина окажется вне пределов зоны устойчивости (рис.12.5). В этом случае необходимо сократить вдвое длину ребер симплекса, причем вершина с наименьшей интегральной оценкой остается неподвижной. В данном случае такой вершиной служит третья точка. Формулы для вычисления координат двух новых вершин очевидны:

После подсчета интегральных оценок получаем

№ точки			Интегр.оценка
3	0.086	0.710	0.16640
5	0.081	1.110	0.21388
6	0.153	0.930	0.39266

Последующие шаги приводят к постепенному уменьшению интегральной оценки переходного процесса. Остановка всей вычислительной процедуры производится по признаку малого выигрыша в интегральной оценке, которая по принятой терминологии в теории наименьших квадратов является функцией риска. В приведенном примере достаточно малой интегральной оценкой можно считать величину I₂ = 0.046608.

3.Метод гармонической линеаризации. Вычисление коэффициентов.

Основная идея метода гармонической линеаризации относится к замкнутому контуру автоматической системы, в котором выделен нелинейный элемент с параметрами, независящими от времени, и остальная часть, описываемая линейным дифференциальным уравнением (рис.23.1).

Рис.23.1. Структурная схема с выделенным нелинейным элементом.

Предположим, что в замкнутом контуре возможен некоторый периодический режим и выход линейной части изменяется по закону . Нелинейный элемент преобразует этот гармонический сигнал в функциюu ( t ), также периодическую, которую можно разложить в ряд Фурье, т.е. представить в виде .

Коэффициенты разложения вычисляются по известным правилам: , при,(23.1).

В этих формулах - период функции.

Главная идея метода состоит в том, чтобы ограничиться в разложении выхода нелинейного элемента гармониками с номером k, не превышающим единицу, т.е. представить этот выход в виде .(23.2)

Здесь мы предположили также, что 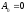. Такой периодический режим мы назовемсимметричными автоколебаниями.

Отбрасывание гармоник более высокого порядка оправдывается тем, что амплитуда их после прохождения линейной части контура уменьшается с ростом частоты. Действительно, как мы видели при изучении линейной теории, передаточная функция линейных динамических систем представляется в виде отношения двух полиномов ,

причем порядок знаменателя обычно превышает порядок числителя. Благодаря этому свойству и происходит подавление высших гармоник сигнала u(t) при прохождении линейной части.

Наша дальнейшая задача состоит в определении параметров установившихся автоколебаний – их амплитуды и частоты. С этой целью приступим к гармонической линеаризации нелинейного элемента с характеристикой 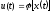. Введем обозначения (см.,например, книгу Е.П.Попова «Теория нелинейных систем автоматического регулирования и управления»,М.: Наука,1979)и. Условимся записывать выражение (23.2) в виде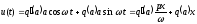. (23.3)

Здесь - символ дифференцирования. Используя формулы (23.1), получаем выражения для вычислениякоэффициентов гармонической линеаризации , 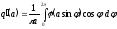(23.4)где.

Собственно гармонической линеаризацией принято называть представление сигнала u(t) в форме (23.3). Переходя в (23.3) к изображениям по Лапласу, запишем . (23.5)

В последнем выражении мы узнаем аналог передаточной функции нелинейного элемента, который с полным основанием можно обозначить символом . Полагая, найдем такжеаналог частотного оператора нелинейного элемента .(23.6)

Обращаем внимание читателя, что на этот раз правая часть (23.6) зависит не от частоты, а от амплитуды входного сигнала в нелинейный элемент. Однако эта амплитуда формируется при прохождении линейной части. Таким образом, параметры автоколебаний зависят как от линейной части, так и от характеристики нелинейного элемента.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 11