Задание для группы иу-10-12
Таблица 11
|
№ Вар. |
f |
№ Вар. |
f |
|
1 |
1,2,6,10, (3,7,10,19,20,21,). |
14 |
9,11,15,25,27,(13,24,26,28,29,30,31) |
|
2 |
2,4,10,22,,(0,5,8,12,13,18,20,24). |
15 |
3,6,18,19,(7,13,15,22,31) |
|
3 |
0,1, 9,13, (4,10,21,22,25). |
16 |
11,15,26,31,(9,13,14,29,30) |
|
4 |
0,2,6,14, (1,3,12,17,20,22,24). |
17 |
2,4,8,10,(6,12,14, 24,28) |
|
5 |
1,9,13,17, (6,7,14,21,23,25,31). |
18 |
18,20,24,28,(8,12,22,26,30). |
|
6 |
2,4,12,14, (7,11,15,23,26,30). |
19 |
19,21,27,31,(1,5,9,13, 29). |
|
7 |
1,3,7,11, (0,4,13,21,22). |
20 |
2,3,6,14,(7,11,15,18,22). |
|
8 |
10,12,26,27, (13,15,22,25,30). |
21 |
19,23,30,31,(3,7,11,15,26,27) |
|
9 |
14,15,28, (6,13,18,22,30,) |
22 |
20,21,27,28,( 8,4,12,17,30) |
|
10 |
8,13,23,27, (1,5,9,17,21,25). |
23 |
1,4,6,7,(2,3,5,16,17,) |
|
11 |
5,9,17,27,(4,6,13,14,25,30) |
24 |
9,13,19,27,(3,5,7,9,11,,31,) |
|
12 |
5,12,20,29,(13, 17,21,24,25,28) |
25 |
5,9,13,17, (4,13,21,22,25) |
|
13 |
14,18,20,24, (0,4,8,12,22,26,) |
26 |
19,23,30,31,(3,7,11,15,22,26) |
Задание для группы иу-10-13
Таблица 12
|
№ Вар. |
f |
№ Вар. |
f |
|
1 |
2,6,14, 24,(3,7,10,19,20,21,). |
14 |
9,11,15,27,(13,24,26,28, 30,31) |
|
2 |
4,16, 26,30,(0,2,5,8,12,13,24,28). |
15 |
2,3,6,19,(7,13,15,22,23,29,) |
|
3 |
1,5,17,29,(4,13,21,22,25,27). |
16 |
10,11,15,26,(9,13,14,25,27,29,30) |
|
4 |
0, 8,16,28,(1,3,12,17,19,20,). |
17 |
0,2,8,10,(6,12,14,16,20,24,28) |
|
5 |
3,15,19,27,(6,7,14,22,30,31). |
18 |
16,18, 24,28,(0,4,8,12,22,30). |
|
6 |
2,6,10, 22,(7,14,15,23, 31). |
19 |
17,19,21,31,(1,5,9,13,23,25,). |
|
7 |
1, 5,9,13, (4,13,21,22, 25,27). |
20 |
2,3,,10,14,(7,11,15,18,22,26,). |
|
8 |
12,14,29,31,(13,15,17,27,30). |
21 |
18,19,23,30,(3,7,11,15,22,26,) |
|
9 |
12,13,15, 31,(2,6,14,18,22, 30,) |
22 |
16,20,21,28,( 8,4,12,17,,30) |
|
10 |
8,10,24,26, (1,5,9,11,21,25). |
23 |
0,1,4, 7,(2,3,5,16, 18,19) |
|
11 |
1,5, 17,29,(4,6,21,25,30) |
24 |
1,9,19,27,(3,5,7,9,11,23,31,) |
|
12 |
4,5, 20,29,(13,16,17,25,28) |
25 |
1,5,9,29,(4,13,22,25,27) |
|
13 |
14,20,24,28,(0,4,8,12,22,26,30,) |
26 |
17,19,23,31,(3,7,11,15,22,28) |
Пример 5:.
Минимизировать не полностью
определенную функцию
с помощью метода Бицена и проверить
результат с помощью развертки пятимерного
куба.
f = 2,3,6,18,19,(7,13,15,22,23,29,31)
Решение:
*
|
№ |
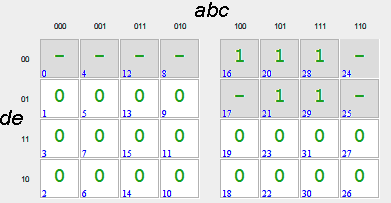
Покрытие |
Образованное покрытие |
|
2 |
+ |
[3/1],0/2,[6/4],10/8,[18,16],(7/1,4),(22/4,16),(23/1,4,6) |
|
3 |
+ |
(2/1), 1/2, (7/4), 11/8, [19/16],[6/1,4],(23/4,16),(22/1,4,16) |
|
6 |
19 |
(7/1), 4/2, [2/4], 14/8, (22/16), [3/1,4],[18/4,16],[19/1,4,16] |
|
18 |
+ |
|
|
19 |
+ |
|
Вывод:
По таблице метода Бицена видно, что все
обязательные наборы функции покрываются
одним членом: 19. Так как он сам обязательный,
то можно исключить 3 переменных,
соответствующих числам 16, 4, 1, т.е.
переменные
.
6 =
=
168421
Получаем, что, сверяя полученный результат с картами Карно, можно с уверенностью сказать, что других минимальных форм для этой функции не существует.