студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki

Таким образом, в области длинных волн обычный закон дисперсии для звуковых волн, распространяющихся со скоростью

.

Обратимся вначале к первому следствию. Из соотношения (8.6) следует, что одна и та же частота колебаний может соответствовать разным длинам волн. Нам надо выяснить, являются ли колебания, отличающиеся от данного на величину 2

( — целое число), тождественными, либо они имеют одинаковые частоты, но физически это разные колебания. Вычислим для этого отношение амплитуд колебаний атомов в двух узлах

1 и 2:

Итак, мы показали, что физически эти колебания полностью тождественны, т. е. мы действительно в зоне Бриллюэна получаем все физически различные типы колебаний. Почему колебания с разными оказались тождественными? Дело в том, что в дискретной цепочке, обладающей трансляционной симметрией, все равно какой длине волны приписывать, например, противофазное движение частиц — 2 или 2 2 1 . И в том, и в другом случае мы получаем одинаковые колебания соседних атомов. На рис. 8.3 показана

из расположенных на расстоянии попеременно частиц массойи . Пусть тяжелые частицы занимают четные позиции, а легкие — нечетные. Уравнения движения теперь примут вид

Будем искать решение, как и раньше, в виде плоских волн и в результате мы получим дисперсионное уравнение в виде

462 Динамика атомов кристаллической решетки. Фононы [ Гл. 8

где

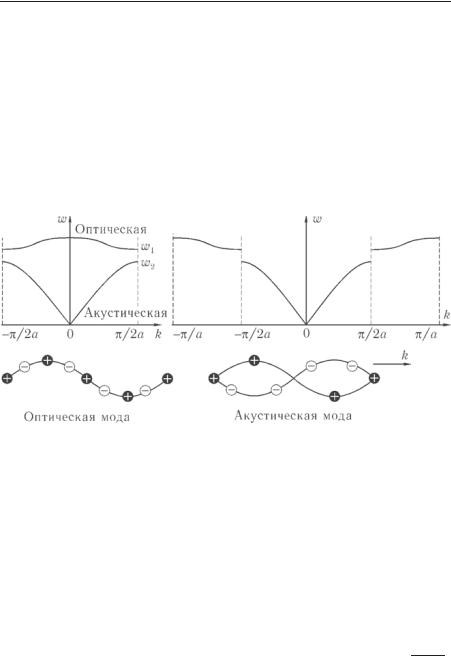
Теперь в спектре колебаний появилось две ветви, соответствующие разным знакам в скобке выражения (8.11) — низкочастотная, соответствующая знаку « » (ее называют акустической, она полностью аналогична колебаниям линейной цепочки из одинаковых частиц), и высокочастотная — оптическая. На рис. 8.4 показан вверху — спектр колебаний линейной цепочки, составленной из частиц с разными массами, в двух представлениях; слева — в диапазоне волновых чисел от 2 до

2 ; справа — от до ; внизу — движение атомов,

Рис. 8.4

соответствующее акустической и оптической модам. При малых значениях ( 1) выражения для акустической и оптической частот колебаний приобретают вид

Оптическая ветвь соответствует противофазным колебаниям частиц и ее характерной особенностью является то, что при малых значениях волнового вектора частота колебаний оказывается максимальной, а не минимальной, как это имеет место в акустической ветви. Кроме того, в спектре возбуждений появилась щель, так что максимальная частота акустических коле-

баний (при 2 ) равна 2 , а минимальная частота

оптических колебаний (также при 2 ) равна 2 . Зона Бриллюэна теперь простирается от 2 до 2 , т. е. период решетки 2 . При переходе к цепочке из одинаковых частиц ( ) щель в исчезает, период решетки становится равным . Если мы остаемся в половинной зоне Бриллюэна,

то оптическая ветвь становится как бы зеркальным отражением акустической относительно 2 .

Итак, мы показали, что колебания атомов кристаллической решетки могут быть представлены в виде гармонических колебаний, частота и волновой вектор которых связаны определенным соотношением (законом дисперсии). Тем самым мы показали, что энергия взаимодействующих друг с другом атомов (ионов, молекул) оказалась равной сумме энергий не взаимодействующих друг с другом осцилляторов. Осциллятор играет роль структурной единицы движения в кристалле. С точки зрения колебательной энергии кристалла твердое тело представляет собой «газ» осцилляторов, так как именно в газе энергия — сумма энергии отдельных частиц.

Этот вывод имеет столь принципиальное значение для физики твердого тела, что имеет смысл обсудить его более подробно.

Возбуждение кристаллической решетки (тепловой нагрев) приводит к очень сложному движению составляющих ее частиц — атомов, ионов, молекул. При прямолинейном подходе решетка представляет собой набор отдельных атомов, колеблющихся около положения равновесия и передающих избыток энергии при случайных столкновениях. Вообще говоря, этот механизм в принципе правилен, но в рамках такого подхода отыскание законов движения огромного числа атомов является безнадежной задачей. Такую модель индивидуальных частиц удобно заменить коллективной моделью и, действительно, представление возбуждения решетки в виде совокупности бегущих плоских волн позволило нам свести задачу к возбуждению независимых гармонических осцилляторов. Твердое тело — система сильно взаимодействующих частиц, и поэтому возможность сведения этой задачи к задаче о системе слабо взаимодействующих или даже идеальных (невзаимодействующих) частиц является принципиальным моментом. Каждая нормальная мода описывает колебания всей совокупности атомов, но математически это выглядит как колебания простого осциллятора.

Обычно вместо того, чтобы говорить о нормальных модах, пользуются эквивалентным корпускулярным подходом. Конечно, это абсолютно эквивалентные описания. Корпускулярноволновой дуализм позволяет создать удобный, наглядный и очень плодотворный язык для описания поведения атомов твердого тела, язык, особенно пригодный при низких температурах.

Идеология построения подхода к распространяющимся по кристаллу волнам крайне проста. Каждой волне, следуя идеям де Бройля, можно сопоставить частицу, называют ее фононом. Это название квантам звука было дано в 1932 г. советским физиком Я. И. Френкелем (1894–1952). Конечно, фонон это не частица в буквальном понимании этого слова и поэтому элемен-

тарное возбуждение кристалла называют квазичастицей, а совокупность элементарных возбуждений — газом квазичастиц. Просто величины, описывающие макроскопические свойства твердых тел, выражаются в терминах, характеризующих отдельные квазичастицы: их скорость, длину свободного пробега и т. п. Правда, если функциональные зависимости энергии от импульса для всех нерелятивистских частиц одинаковы: 2 2 , отличаясь только массами, у квазичастиц они сложны и многообразны. Фактически для фононов понятие массы теряет смысл, ибо соотношение между энергией и импульсом зависит от величины импульса, а потому масса не является постоянной величиной, т. е. характерным параметром системы. Причина этого в том, что частицы «живут» в однородном и изотропном пространстве, а квазичастицы «живут» в периодической структуре — в кристалле, находящемся в основном состоянии. Иначе говоря, введенные нами квазичастицы (фононы) — это возбужденные состояния кристалла, а вакуум относительно квазичастиц — это кристалл в основном, невозбужденном состоянии.

Впервые распространил квантовомеханические соотношения де Бройля на описание волн в кристалле в 1929 г. советский физик=теоретик И. Е. Тамм (1895–1971).

8.2. Изучение фононного спектра кристаллов методом неупругого рассеяния нейтронов

В гл. 7 мы рассмотрели вопрос об исследовании кристаллических структур твердых тел методом упругого рассеяния различных частиц — рентгеновских лучей, нейтронов, электронов. При взаимодействии частиц с кристаллической решеткой с определенной вероятностью могут, конечно, происходить и неупругие процессы. При неупругом рассеянии рентгеновских лучей или нейтронов изменяется не только направление вектора k, но и его величина, т. е. длина волны (и частота). Падающая рентгеновская или нейтронная волна возбуждает механические колебания атомов кристалла вблизи их положения равновесия. При этом она может как отдавать энергию возбужденным колебаниям, так и поглощать энергию уже имеющихся тепловых колебаний.

При взаимодействии какой-либо частицы с кристаллической решеткой механическая энергия колебаний может измениться только на величину, кратную энергии фонона . Если падающая частица обладает энергией и импульсом p, а импульс фонона равен , то законы сохранения энергии и импульса для процесса неупругого рассеяния с рождением (поглощением) фонона имеют вид

8.2 ] Изучение фононного спектра кристаллов 465

Подставляя значение из первого уравнения во второе, получим

Отношение скорости звука в твердом теле к скорости света порядка 10 5, максимально возможная величина 2 (это соответствует условию ), что соответствует максимальной энергии фонона 2 . Отсюда следует, что максимально возможное относительное изменение энергии рентгеновского кванта равно

Таким образом, экспериментально наблюдать неупругое рассеяние рентгеновских квантов на кристаллической решетке практически невозможно: необходимы как крайне высокая монохроматичность падающих лучей, так и очень высокая разрешающая способность детекторов рассеянного излучения.

Иная ситуация возникает при рассеянии медленных нейтронов, для которых законы сохранения (8.14) можно записать в виде

где — масса нейтрона. Будем для простоты оценок считать, что рассеяние нейтронов изотропно. Тогда среднее значение импульса фонона 2 , и изменение кинетической энергии нейтрона будет порядка

Таким образом, в случае нейтронов, имеющих скорость порядка скорости звука, изменение энергии оказывается порядка

их начальной энергии. Как раз такую скорость имеют тепловые нейтроны, источником которых являются, в частности, ядерные реакторы.

Чтобы измерить импульс и энергию фонона (или какого-либо другого типа возбуждений кристалла), в частности, магнона — кванта магнитных возбуждений, надо знать импульс и энергию падающей частицы и импульс и энергию рассеянной. Обычно эксперименты проводят с монохроматическими нейтронами, так что достаточно измерить угол рассеяния и энергию рассеянного нейтрона.

8.3. Эффект Мёссбауэра

Дифракция электромагнитных и нейтронных волн в кристаллах позволяет нам как исследовать структуру кристаллической решетки при упругом рассеянии, так и изучать колебания атомов решетки при неупругом рассеянии. Любое движение атомов решетки должно, казалось бы, приводить к возбуждению фононов, т. е. передаваться всему кристаллу. Однако так казалось лишь до 1957 г., когда немецкий физик-экспериментатор Р. Мёссбауэр (р. 1929) обнаружил процесс бесфононного снятия возбуждения атомов. Этот эффект — эффект Мёссбауэра — называется также эффектом резонансного поглощения -лучей без отдачи или ядерным гамма-резонансом (ЯГР).

Резонансное поглощение для света впервые экспериментально наблюдалось в 1904 г. американским физиком-эксперимента- тором Р. Вудом (1868–1955). Сущность резонансного поглощения заключается в том, что если атом облучать светом с частотой, соответствующей энергии возбуждения его электронов, то поглощение света будет носить резонансный характер. Казалось бы, аналогичное явление должно наблюдаться и в ядрах, если их облучать -квантами, соответствующими энергии нуклонных возбуждений. Однако в отличие от атомов, на ядрах в обычных условиях резонансного поглощения не происходит.

Все дело в том, что у свободного ядра энергия ядерного перехода 0 делится между -квантом с энергией и ядром, испытывающим отдачу в силу законов сохранения энергии и импульса:

Как правило, энергия -излучения ядер лежит в диапазоне 10–1000 кэВ, что много меньше энергии покоя ядра я 2

8.3 ] Эффект Мёссбауэра 467

Так как при комнатной температуре тепловые скорости атомовт примерно в 106 раз меньше скорости света, то в силу эффекта Доплера энергия испускаемых ядром-квантов не только уменьшается на величину энергии отдачи ядра, но и размывается на величину порядка

Энергетическое распределение -квантов, вылетающих из свободных атомов, будет иметь вид, показанный на рис. 8.6 б — пик при значении энергии 0 шириной . Точно так же линия поглощения будет сдвинута относительно энер-

Конечно, изменения энергии испускаемых фотонов имеют место и в случае излучения света атомами, но в оптической области сдвиг энергии в 1012 раз меньше, так как энергия испускаемого светового кванта порядка нескольких электронвольт, т. е. в 106 раз меньше, чем -кванта. По этой причине в оптической области спектра резонансное поглощение света атомами легко наблюдается — сдвиг по энергии намного меньше естественной ширины линий испускания.

Спектры испускания и поглощения -квантов ядром атома, входящего в состав кристалла будут точно такими же. При излучении -кванта атом получает импульс и энергию отдачи, которые приводят к последующим колебаниям решетки. Иначе говоря, процесс излучения -кванта из ядра сопровождается рождением фононов в кристаллической решетке. Ввиду большой величины при испускании одного -кванта может родиться много фононов. Их рождение соответствует тепловому уширению линии -спектра и сдвигу относительно 0 на величину энергии отдачи .

Заслуга Мёссбауэра состоит в том, что он показал, как можно уничтожить энергию отдачи. Если мы хотим избавить ружье от движения отдачи, чтобы вся энергия заряда передавалась пуле, надо прикрепить ружье к какому-либо массивному телу.

Чтобы то же самое сделать в случае испускания -кванта ядром, надо закрепить ядро в решетке кристалла. Мёссбауэр понял, что при достаточно низких температурах, когда в кристалле мало фононов, существует заметная вероятность процесса излучения -кванта ядром без последующего рождения фононов. Чем ниже температура кристалла, тем меньше вероятность рождения фононов в результате испускания -кванта ядром атома, расположенного в решетке кристалла. Иначе говоря, кристалл ведет себя как единое целое и воспринимает импульс отдачи целиком. При этом в формулe для энергии отдачи вместо я оказывается масса всего кристалла и энергия отдачи становится пренебрежимо малой. Испускание и поглощение -квантов без отдачи импульса и составляет сущность эффекта Мёссбауэра.

Бесфононный характер эффекта Мёссбауэра означает, что атомы как-бы не участвуют в тепловом движении, т. е. линия-излучения не уширена за счет эффекта Доплера (по имени австрийского физика Х. Доплера (1803–1853)). Ее ширина оказывается равной естественной ширине линии, определяемой временем жизни возбужденного состояния ядра ; обычно она составляет 10 8–10 10 эВ, что на 4–5 порядков меньше тепловой доплеровской ширины . Несмещенную линию -из- лучения, имеющую естественную ширину, называют мессбауэровской линией.

На первый взгляд отсутствие доплеровского уширения кажется парадоксальным, так как скорости теплового движения атомов составляют 102–103 м/с, что в силу эффекта Доплера должно приводить к уширению линии до 10 1–10 2 эВ, т. е. на шесть–семь порядков больше естественной ширины. Все дело в том, что при оценке ширины линии испускания мы должны учитывать большую частоту тепловых колебаний атомов, которая составляет 1012–1013 Гц (как будет показано в § 8.4, оценить частоту колебаний решетки легко из равенства

Б , где — температура Дебая). Время жизни ядерных уровней, используемых в эффекте Мёссбауэра, составляет обычно 10 7–10 8 с. При беспорядочном тепловом движении атомов за это время происходит большое число тепловых колебаний атомов, из-за эффекта Доплера частота излучаемого кванта при этом с равной вероятностью как увеличивается, так и уменьшается, и в результате усреднения этих сдвигов линейный по скорости обычный эффект Доплера практически равен нулю. Относительный сдвиг частоты определяется только средним

квадратом скорости, вернее он равен величине 2 2 2, которая мала по сравнению с естественной шириной линии испускания.

Чрезвычайно малая относительная ширина мессбауэровской линии 0 10 12–10 14 (а в некоторых ядрах она равна да-

эти частицы являются бозонами. Откуда следует, что фонон — это бозе-частица? В твердом теле звуковые волны могут быть продольными и поперечными, причем имеются две независимые поперечные поляризации. Таким образом, у фонона возможны при заданном импульсе, а значит при одной и той же энергии, три различных состояния. Мы говорим в таком случае, что состояние трехкратно вырождено, но степень вырождения равна 2 1, где — спин частицы. Таким образом, формально спин фонона равен единице, а это означает, что он описывается бозе-статистикой.

Итак, по своим свойствам фонон почти полностью аналогичен фотону, и мы можем использовать для описания свойств фононного газа уже полученные нами соотношения для фотонов. Обратимся вначале к вопросу о теплоемкости решетки. Вычисление теплоемкости мы начнем с расчета внутренней тепловой энергии тела, так как теплоемкость есть не что иное, как изменение тепловой энергии при изменении его температуры на один градус. Так как колебательная энергия кристалла «заключена»

вгазе осцилляторов, то, естественно, надо вычислить среднюю энергию этого газа, но мы это уже делали для фотонов, и чтобы воспользоваться уже полученными формулами, надо выяснить,

вчем различие между фотонами и фононами.

Звуковые фононы практически полностью аналогичны фотонам, ибо и те и другие описываются одним и тем же законом дисперсии: для фотонов , а для звуковых фононов . П. Дебаем (1884–1966) было сделано следующее предположение: будем считать, что линейный закон дисперсии справедлив во всем диапазоне и . В таком случае отличие фононов от фотонов заключается лишь в следующем.

1.В закон дисперсии фотонов входит скорость света, у фононов — скорость звука;

2.Степень вырождения у фотонов равна 2, а у фононов — 3;

3.Фотоны могут быть любой частоты — от 0 до , а фононы сверху ограничены максимальным значением.

Это означает, что энергия единицы объема кристалла при заданной температуре равна

0

Мы воспользовались уже полученным ранее для фотонов выражением (6.18) для энергии, но при этом заменили скорость света на скорость звука, учли разную степень вырождения у этих частиц (коэффициент 3/2) и интегрирование производится не до , а до . В принципе мы должны были учесть, что поперечные и продольные звуковые волны имеют разную скорость,