1. Дифракция на прямоугольной апертуре.

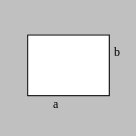
В этом случае

Амплитуда равна 0 при , где

Условие минимума

2. Дифракция на круглом отверстии.

3. Для описания дифракции на круглом отверстии необходимо перейти в полярные координаты в плоскости объекта и в плоскости, в которой рассматривается дифракция. . Функция пропускания для отверстия радиуса имеет вид:

.

Y₁

X₁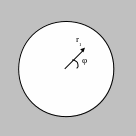

Примечание: , где -функция Бесселя 0-ого порядка.

Свойство функции Бесселя

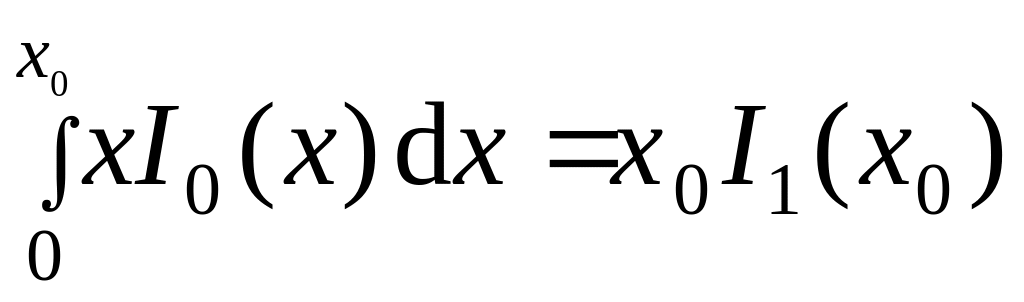
{ ДВА рисунка графика функции Бесселя}

x=3.83, 7.01-1-вые о функции Бесселя

4. Разрешающая способность телескопа

{Рисунок}

- самый большой телескоп в СССР.

Спичка с расстояния 500 км.

Оптика . В электронной микроскопии

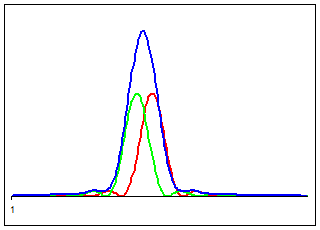
5. Дифракция Гауссова пучка.

Получили функцию Гаусса от .

Функция гладкая не имеет минимума {Рисунок}

Дифракция на периодических структурах

или

,где =1,2,3…

1. Дифракция на синусоидальной решетке.

Рассмотрим решетку, пропускание которой описывается функцией , , где - пространственная частота.

При дифракции на такой решетке Фурье амплитуда задаётся:

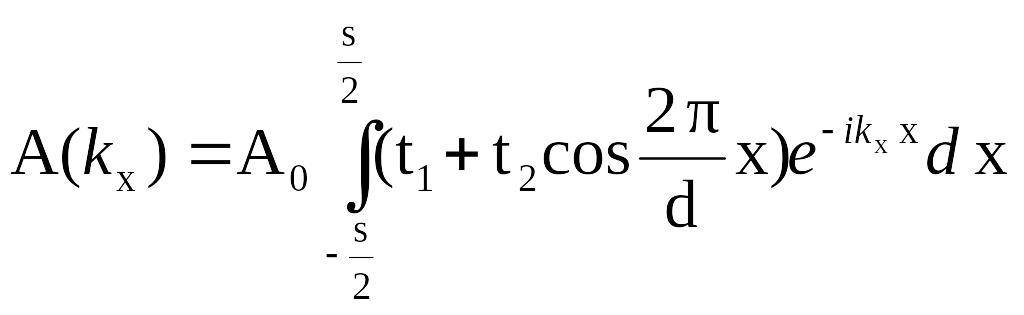,где s- длина решетки.

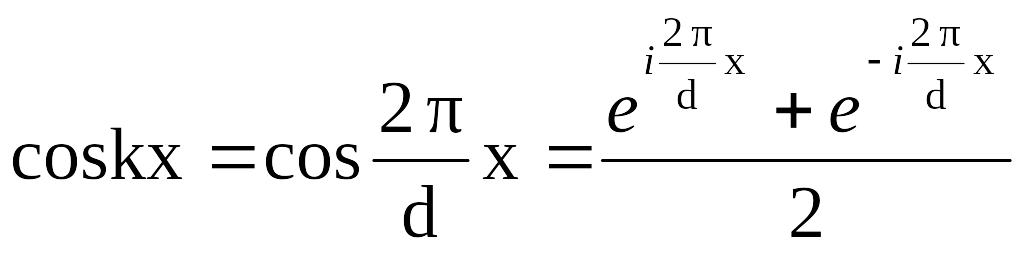,тогда

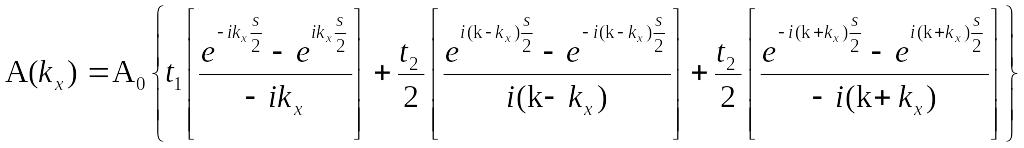
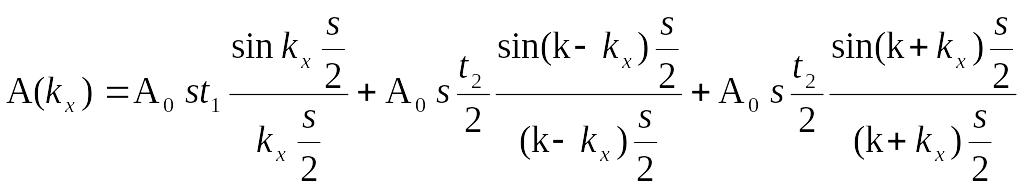, где

Max в следующих точках:

А min в когда (рисунок графика)

Если , то . В этом случае

Рассмотрим периодическую одномерную структуру, описываемую коэффициентом пропускания , тогда периодическая функция может быть разложена в ряд Фурье.

,где

Тогда можно рассмотреть дифракцию на каждой синусоидальных решетках, условие максимума будет иметь вид

т. к. .

А распределение амплитуд будет иметь вид .

Дифракция на амплитудной решетке.

Для случая прямоугольной (одномерной) амплитудной решетки функция пропускания имеет вид (см. рис.3.8):

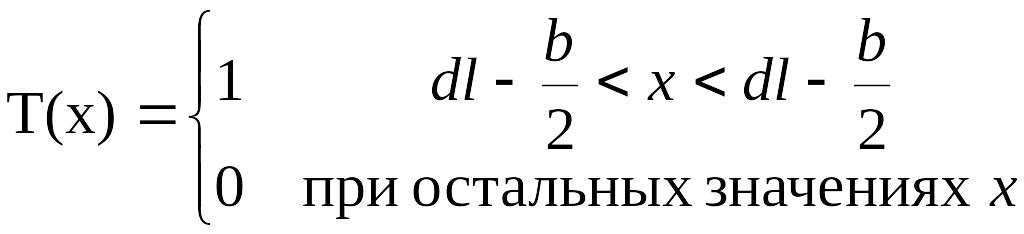
И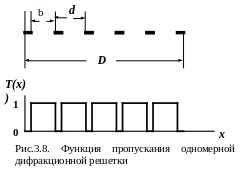 з рис. 3.8 видно, что функция пропускания решетки характеризуется тремя пространственными масштабами: шириной щели b, периодом и полным размером . При интегрировании функции пропускания l-ого штриха можно заметить, что фаза плоской волны состоит из двух слагаемых: первое меняется непрерывно на ширине штриха, второе – дискретно, с шагом , при переходе от одного штриха к другому.

Найдем угловое распределение амплитуд (спектр пространственных частот)

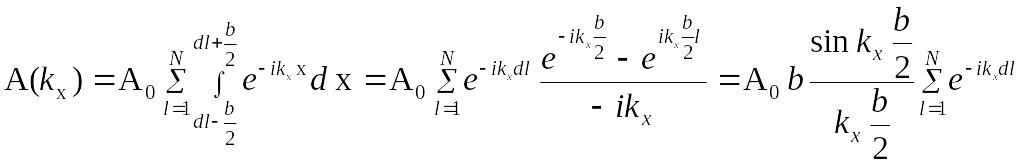
Сумма ряда геометрической прогрессии:

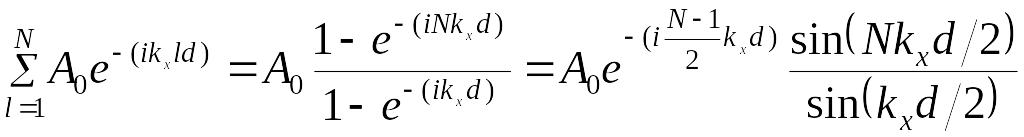
- фазовый множитель, соответствующий волне, распространяющейся от центральной части решетки.

Перейдем к интенсивности:

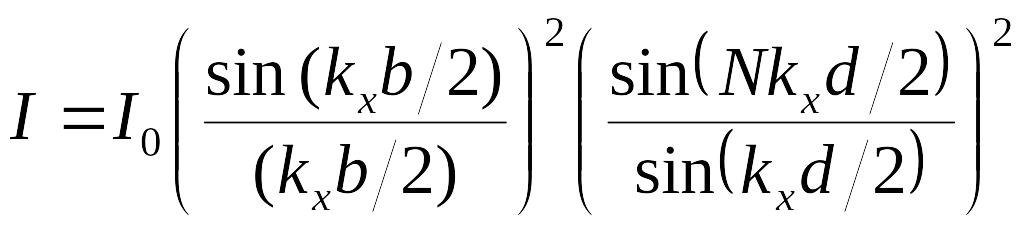(1)

Здесь - интенсивность света, падающего на одну щель,

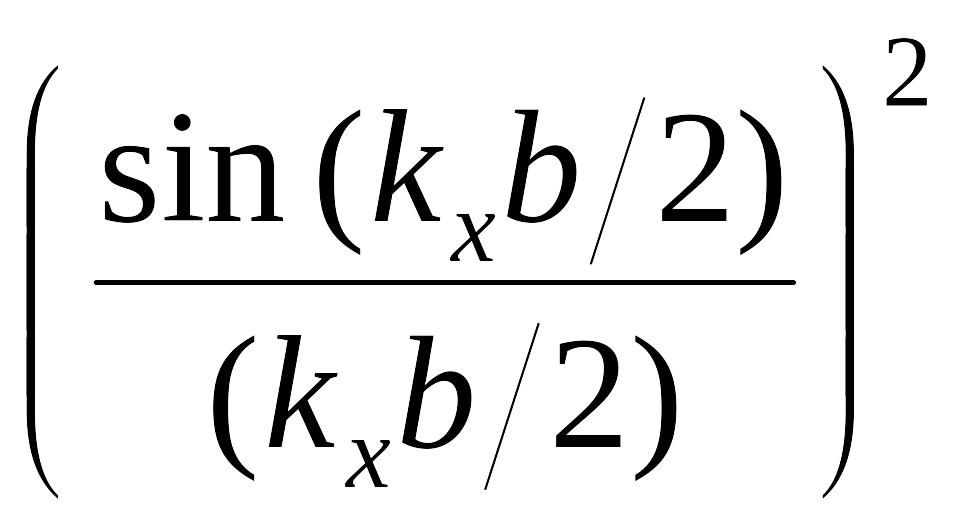(2)

-распределение интенсивности в результате дифракции на щели,

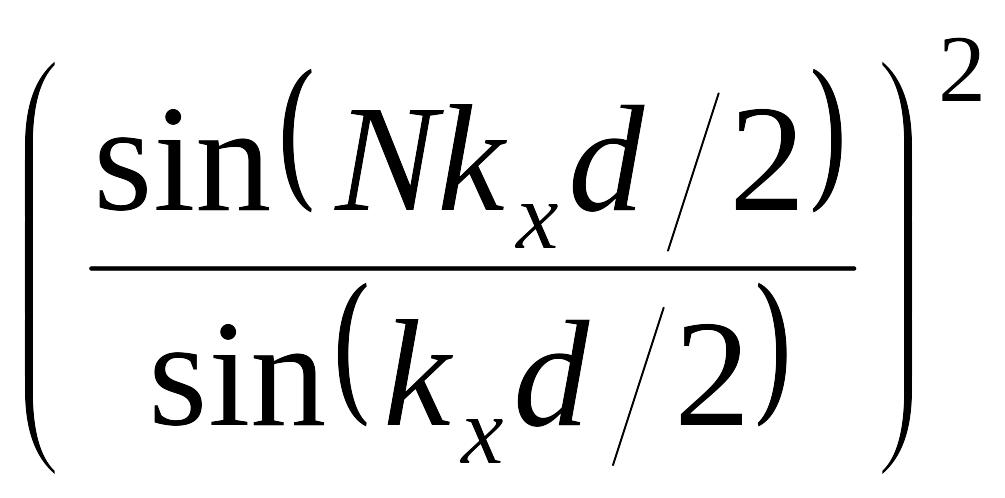(3)

- распределение интенсивности в результате интерференции от N когерентных источников.

Напомним, что

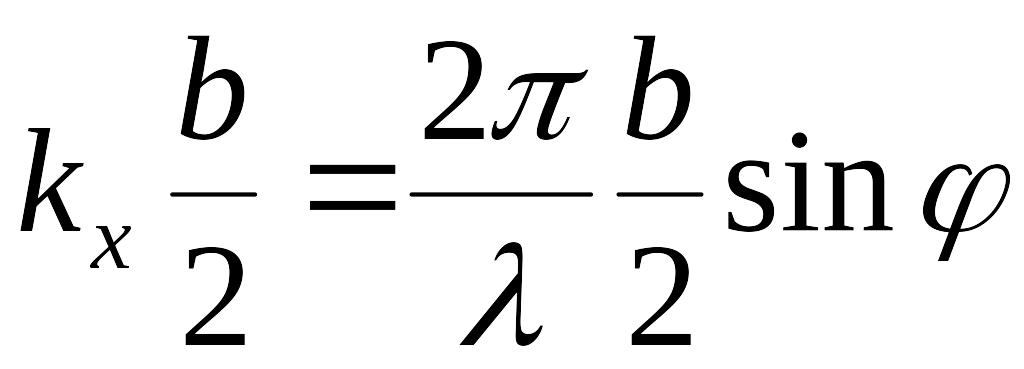
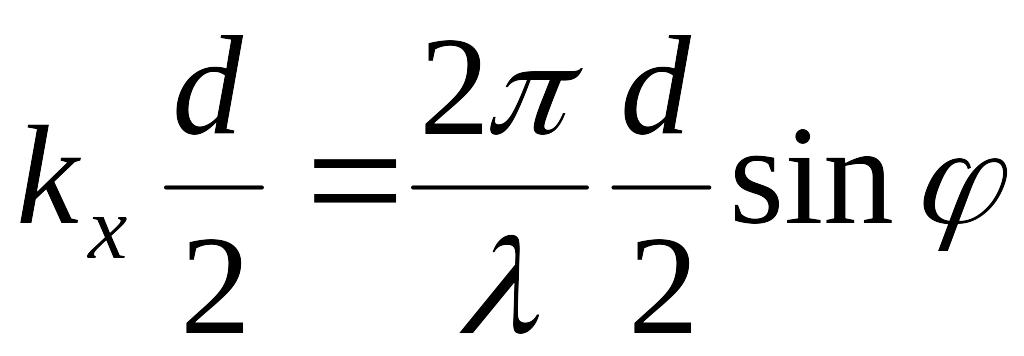
Найдем условия максимумов и минимумов для дифракции на амплитудной решетке.

Интерференционные (главные) максимумы определяются равенством 0 числителя и знаменателя в выражении (2), заметим, что равенство 0 знаменателя, автоматически ведет к равенству 0 числителя, следовательно, условие максимума:

, где

Интерференционные минимумы определяются равенством 0 только числителя при не равном 0 знаменателе в выражении (2). Условия минимума:

, где , то есть между главными максимумами наблюдается -минимум.

Дифракционные минимумы определяются условием , где

Дифракция на двумерных структурах. Двумерная периодическая структура ("двумерная решетка") может быть получена путем наложения двух скрещенных дифракционных решеток. Найти условия максимумов при дифракции света на двумерной решетке, полученной при наложении двух решеток с периодами и в дальней зоне. Штрихи решеток п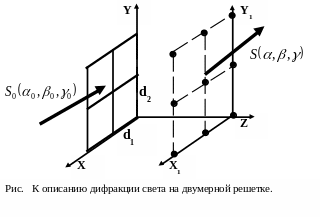 ерпендикулярны друг другу. Свет падает нормально на плоскость решетки.

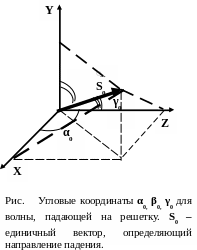
При описании дифракции на двумерных и трехмерных структурах принято переходить к угловым координатам, в качестве которых выступают направляющие углы ( ) для плоскости падения (X, Y) и ( ) для точки наблюдения в плоскости (X₁,Y₁). Введем также единичные вектора для плоскости падения и для точки наблюдения дифракционной картины (рис. ). Данные вектора совпадают по направлению с соответствующими волновыми векторами и . При нормальном падении: .

Максимумы дифракции наблюдаются при одновременном выполнении условий, третье уравнение является свойством косинусов направляющих углов.

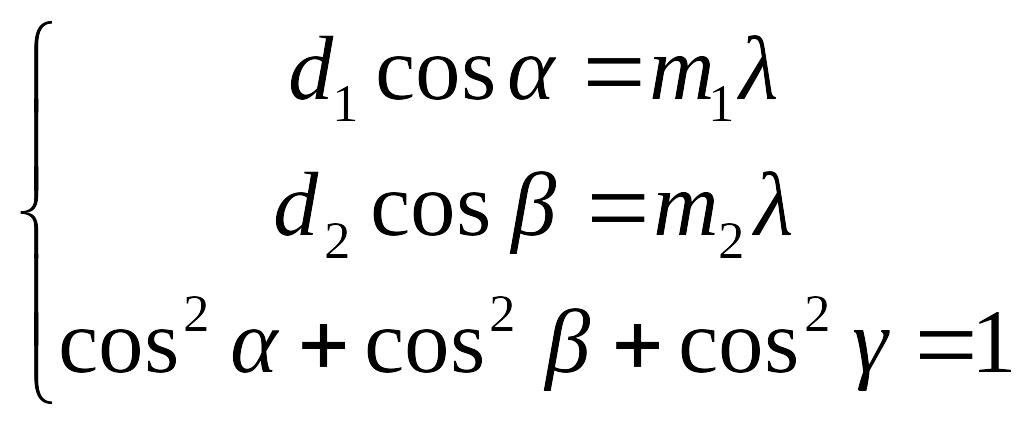
Поэтому картина дифракции в дальней зоне представляет собой набор ярких точек. В данном случае мы получили в плоскости наблюдения Фурье образ двумерной дифракционной решетки.

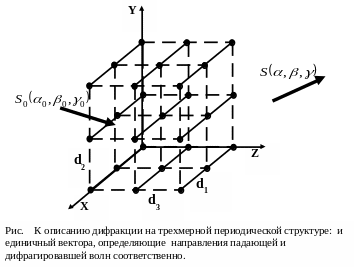Дифракция на трехмерных структурах. Дифракция наблюдается также на трехмерных структурах, т. е. пространственных образованиях, обнаружи­вающих периодичность по трем не лежащим в одной плоскости направлениям. Найти условия образования максимумов при дифракции на трехмерной структуре, показанной на рисунке.

Рассмотрим нормальное падение волны на такую решетку. Максимумы интенсивности появляются при одновременном выполнении условий

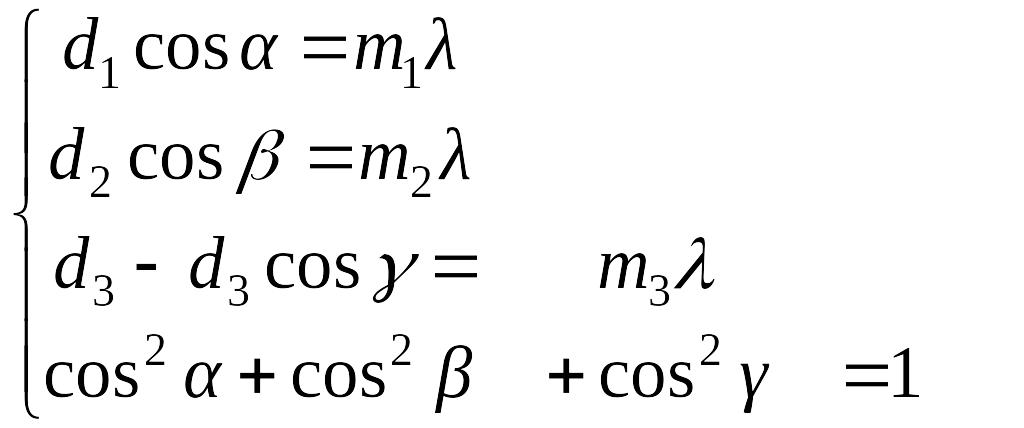
В третьем равнении учтено, что дифракция происходит на слоях, разделенных промежутком и разность хода (рис.)

Очевидно, что информацию о структуре решетки мы можем получить только при условии , при меньших периодах решетки невозможно получить даже первый дифракционный максимум. Система уравнений Лауэ является избыточной в данном случае. При этом длина волны становится четвертым параметром, и данная система уравнений выполняется только для определенных длин волн. Заметим, что при дифракции на объемной решетке требование к монохроматичности излучения снимается. Это широко используется, например, при восстановлении в белом свете голограмм, представляющих собой объемные решетки. Из всего спектра выбирается та волна, для которой выполняются условия Лауэ.

П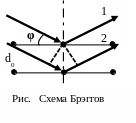 одобными трехмерными структурами являются все кристаллические тела. Однако период их слишком мал для того, чтобы можно было наблюдать дифракцию в види­мом свете. Условие , выполняется в случае кристаллов лишь для рентгеновских лучей. Впервые дифракция рентгеновских лучей от кристаллов наблюдалась в 1913 г. в опыте Лауэ. Полученная система уравнений называется уравнениями Лауэ. Картина распределения максимумов, и в этом случае является Фурье образом объемной решетки и позволяет, выполнив обратное Фурье преобразование расшифровать структуру решетки. Данное явление является основой рентгеноструктурного анализа.

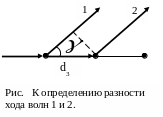
Русский ученый Ю. В. Вульф и английские физики У. Г. и У. Л. Брэгги показали независимо друг от друга, что расчет дифракционной картины от кристаллической решетки можно провести также следующим простым способом.Проведем через узлы кристаллической решетки параллельные равноотстоящие плоскости, они называются атомными слоями. Рассмотрим отражение рентгеновских лучей от двух соседних плоскостей (рис.). Волны 1 и 2 являются когерентными и будут интерферировать между собой. Разность хода , условие максимума будет иметь вид .

Формирование оптического изображения

Рассмотрим поле расходящейся сферической волны, комплексная амплитуда которой на расстоянии от источника имеет вид:

.

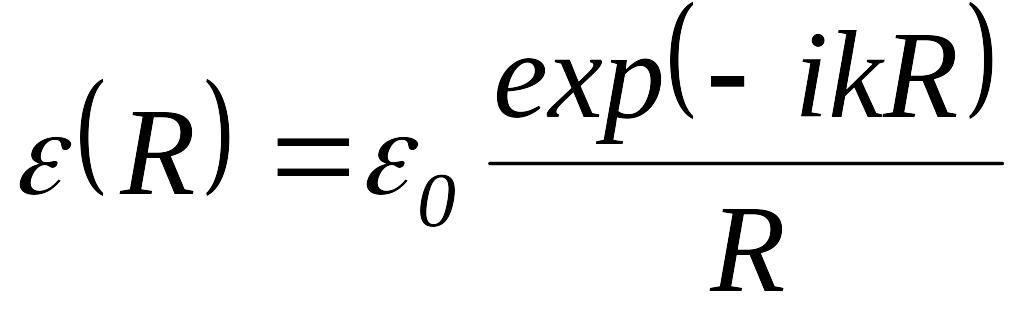Амплитуда поля в плоскости , находящейся на расстоянии от источника, для малых расстояний от оси , т.ч. (в параксиальном приближении), описывается выражением :

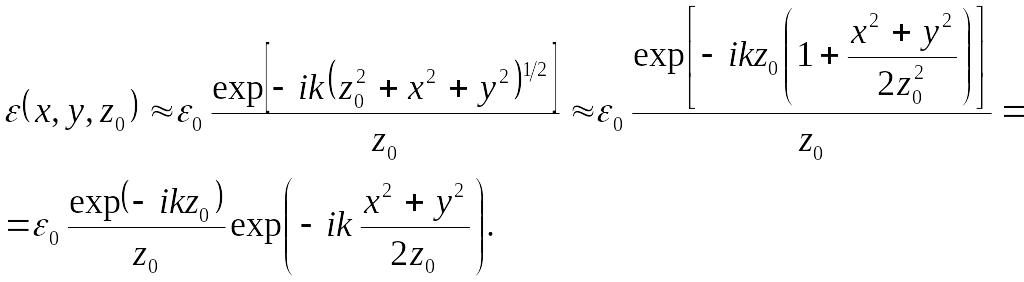
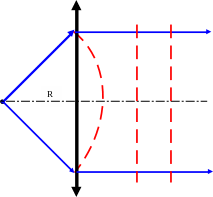
В этом выражении второй множитель описывает задержку фазы колебаний различных точек сферической волны в плоскости относительно оси системы.

Поместим теперь в этой плоскости некоторый объект, компенсирующий задержку фазы. Тогда на выходе объекта формируется волна, колебания всех точек которой происходят с одинаковой фазой, т. е. формируется плоский волновой фронт с амплитудой волны , движущийся по оси .

Функция пропускания такого объекта, называемого линзой, которая компенсирует задержку фазы для параксиальных лучей, очевидно, имеет вид

(3.13)

а расстояние до источника сферического волнового фронта, преобразуемого данной линзой в плоский фронт, назовем фокусным расстоянием и обозначим как Эта величина определяется физическими параметрами линзы: геометрией и размерами преломляющих поверхностей, а также показателем преломления материала . В частности, можно показать, что в параксиальном приближении для простейшего случая тонкой плоско-выпуклой линзы со сферической преломляющей поверхностью радиуса функция пропускания имеет вид (3.13), где

.

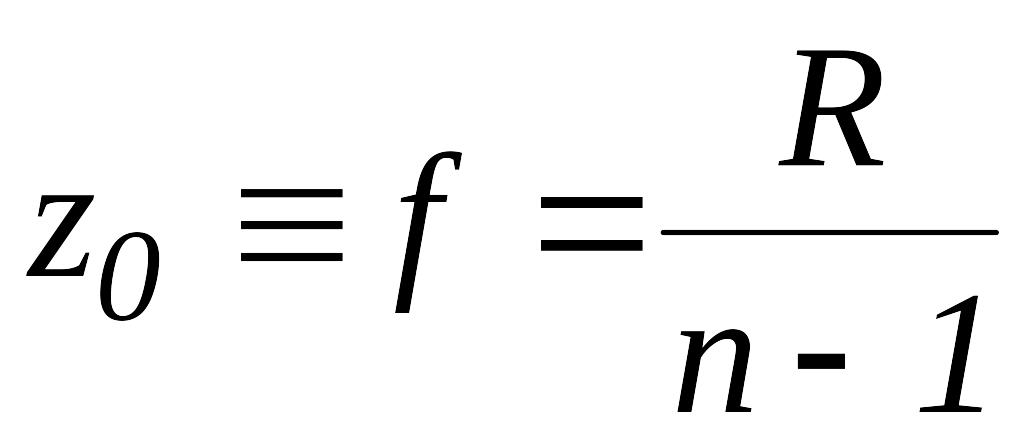Рассмотрим теперь процедуру построения изображения объекта с помощью линзы. В силу симметрии по координатам функции пропускания (3.13), возьмем, для простоты, одномерный объект с функцией пропускания . Полагая, что амплитуда поля волны, падающей на объект равна единице, на выходе получим распределение поля вида . На расстоянии от объекта расположим линзу и построим изображение объекта на произвольном расстоянии от линзы (см. рис. 3.10).

Сначала с помощью интеграла Френеля (3.4) найдем амплитуду светового поля в произвольной точке плоскости на входе линзы :

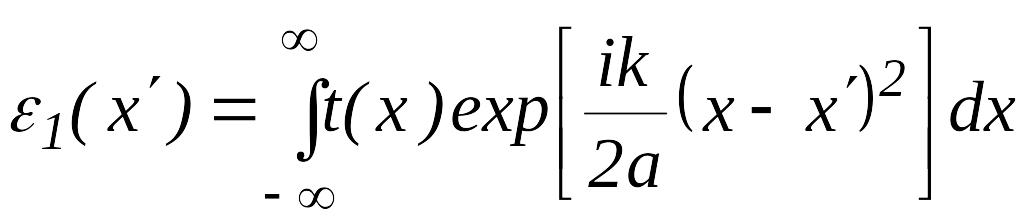. (3.14)

Умножив это выражение на одномерную функцию пропускания линзы, найдем амплитуду поля в той же точке на выходе линзы:

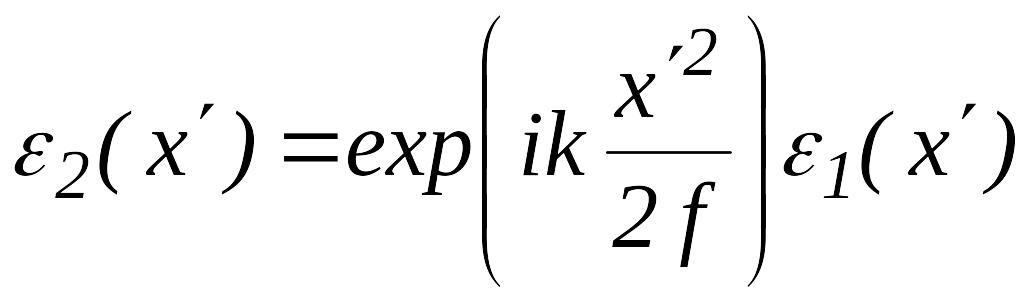. (3.15)

Наконец, амплитуда поля в произвольной точке плоскости, расположенной на расстоянии справа от линзы, описывается выражением:

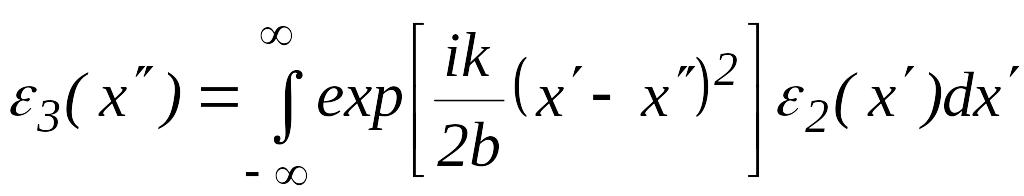(3.16).

Подставив в (3.16) выражения для и , находим после преобразований

, (3.17)

где введены обозначения:

;

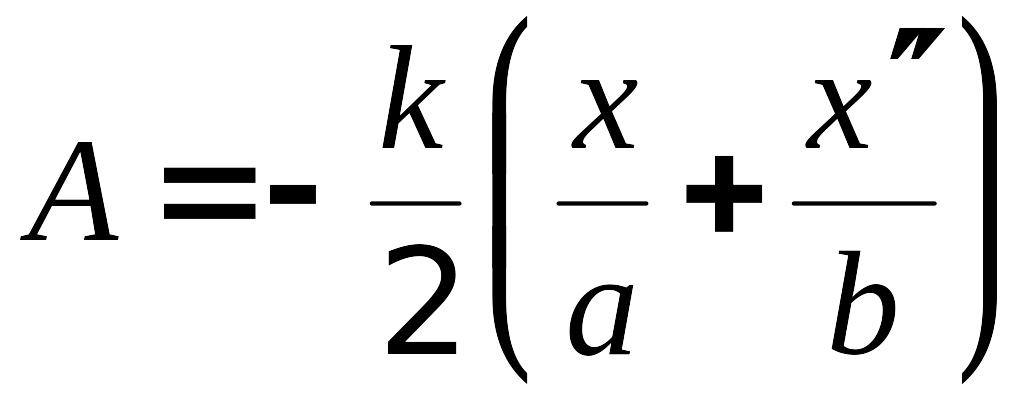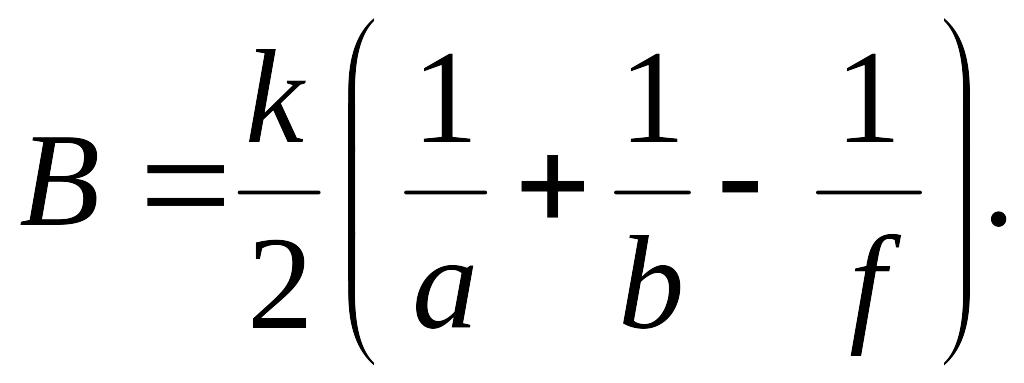
Последний интеграл в (3.17) с учетом формулы

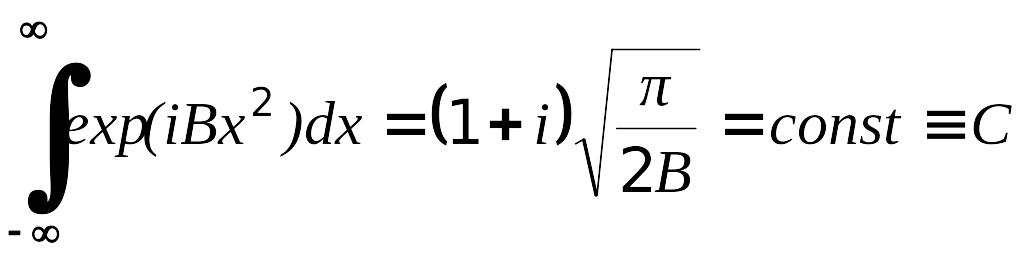
равен .

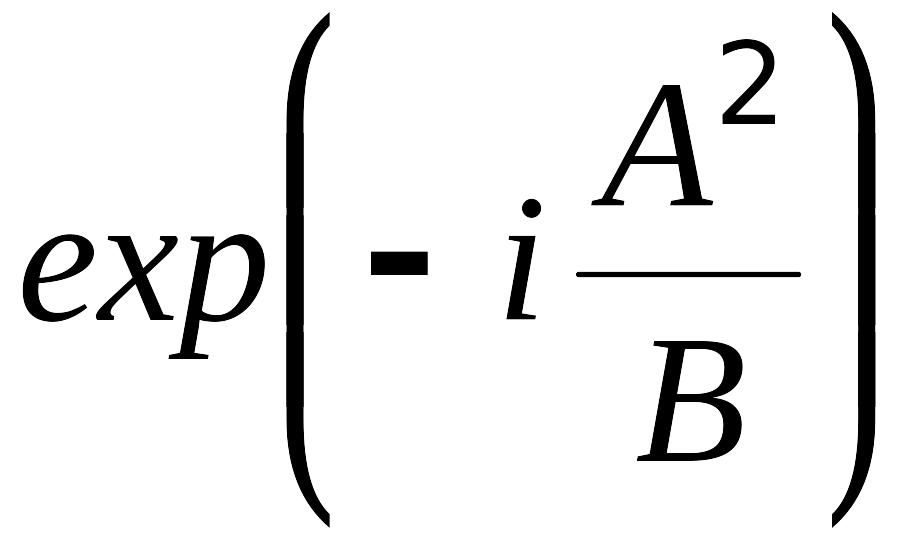Рассмотрим два случая:

1. Найдем распределение амплитуды поля в задней фокальной плоскости линзы, гд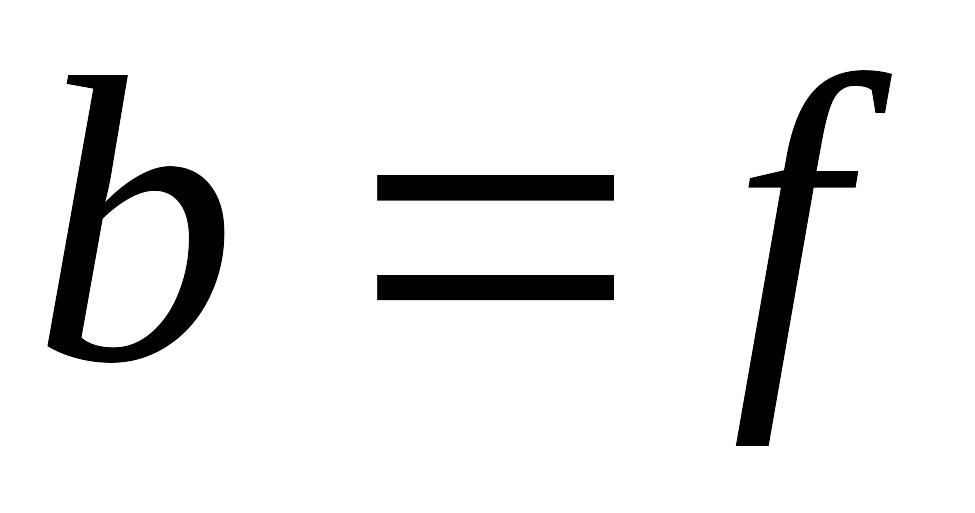е , т.е. 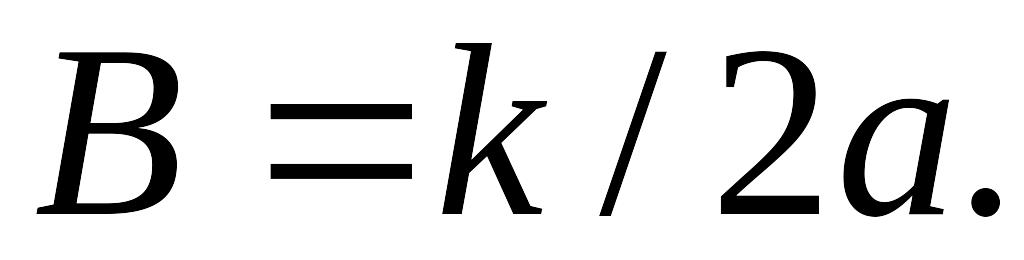Формула (3.17) здесь примет вид:

,

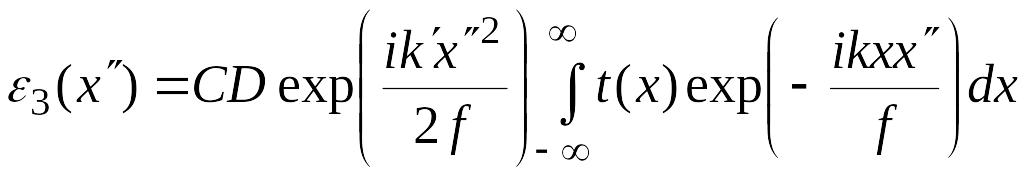где . Отсюда следует, что (с точностью до фазового множителя, не влияющего на распределение интенсивности) в задней фокальной плоскости линзы формируется Фурье-образ функции пропускания объекта по переменной , которая в обычном приближении малых углов дифракции равна поперечной компоненте волнового вектора :

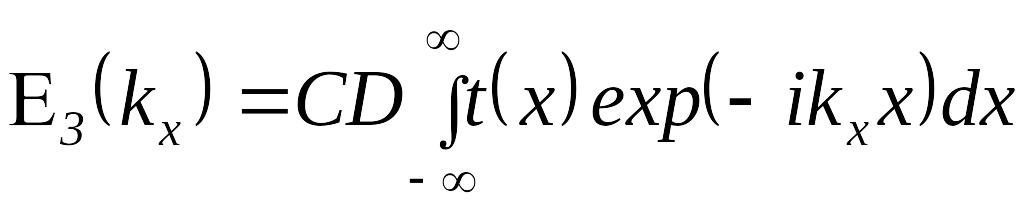. (3.18)

В этом приближении интеграл (3.18) можно также записать в виде, аналогичном формуле (3.7)

.

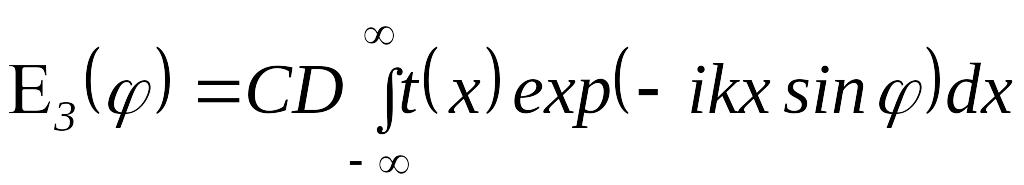2) Найдем распределение амплитуды светового поля в плоскости, расстояние которой от линзы удовлетворяет соотношению:

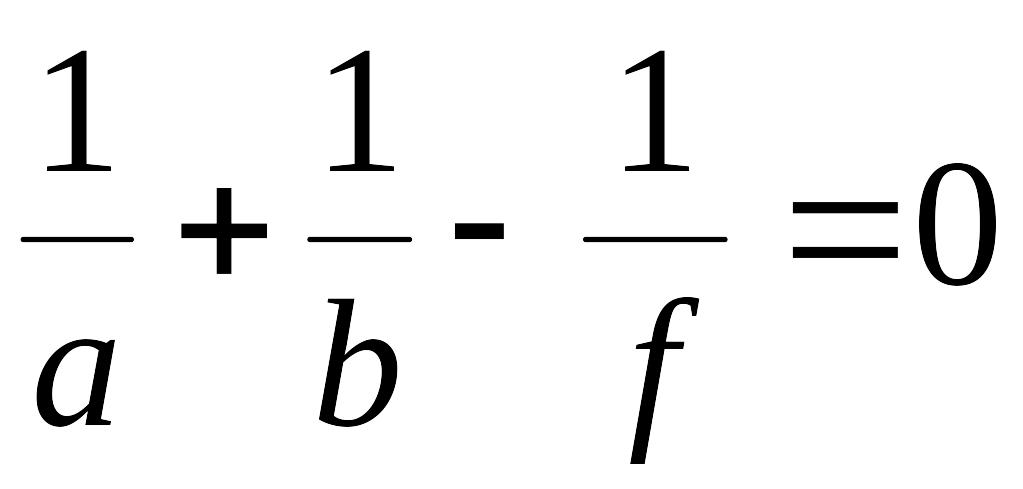, т.е. .

Последний интеграл в (3.17) можно теперь взять в конечных пределах по апертуре линзы, т.е. по отрезку :

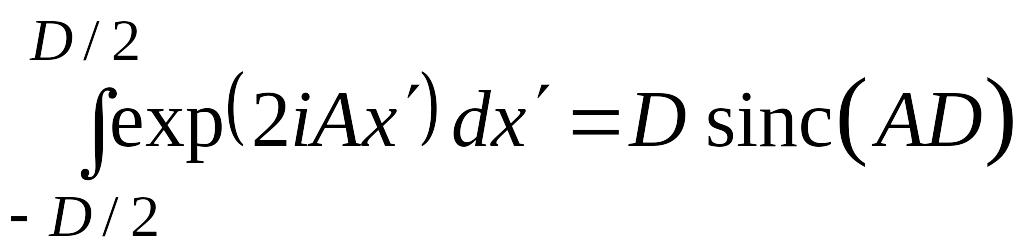. (3.19)

Учитывая, что длина волны мала по сравнению с размером линзы, можно в этом выражении перейти к пределу

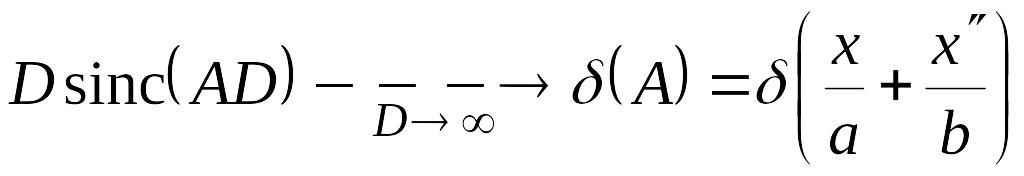, (3.20)

и подставив в интеграл (3.17), найти амплитуду светового поля

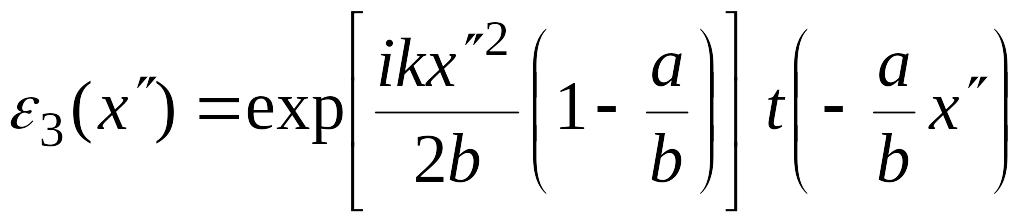. (3.21)

Формула (3.21) показывает, что распределение амплитуды в данной плоскости с точностью до фазового множителя совпадает с распределением амплитуды в плоскости объекта, задаваемым его функцией пропускания . Поэтому рассматриваемую плоскость естественно назвать плоскостью («перевернутого») изображения объекта, масштаб которого как видно из (3.21) увеличился в раз. Описанную процедуру построения изображения объекта в виде дифракционной решетки иллюстрирует рис.3.10.

Из формул (3.19), (3.20) также видно, что точка с координатой в плоскости объекта переводится линзой в точку координатой в плоскости изображения только в случае линзы "бесконечно большой" по сравнению с длиной волны. Если же учитывать конечную апертуру линзы, то вместо точки мы получим в плоскости изображения распределение амплитуды светового поля, описываемое функцией , точнее - с учетом круговой формы апертуры - формулой вида (3.9)'. Характерный угловой размер получившегося светового пятна (Эйри) определяется формулой (3.9") и увеличивается с уменьшением отношения Следовательно, дифракция излучаемой объектом волны на конечной апертуре линзы приводит к "размазыванию" изображения объекта и ухудшению его качества.

Проведенное построение показывает, что формирование линзой изображения объекта, рассматриваемое как дифракционный процесс, можно разделить на два этапа. На первом этапе происходит разложение (анализ) светового поля объекта в Фурье-спектр, который формируется в задней фокальной плоскости линзы. На втором этапе последующее распространение световой волны приводит к восстановлению (синтезу) уже изображения объекта в плоскости изображения. Отсюда следует, что, во-первых, по виду спектра в фокальной плоскости линзы можно установить параметры собственно объекта, во-вторых, воздействуя на спектр объекта, можно управлять параметрами его синтезированного изображения.

Эксперимент Аббе-Портера.

Идея:

Воздействуя на Фурье – образ объекта в фокальной плоскости внести изменения в изображение объекта. Изменения производятся с помощью масок различной формы. Схема одного из классических опытов Аббе по пространственной фильтрации показана на рисунке 4. Расположенная перед линзой проволочная сетка освещается направленным пучком когерентного света. В задней фокальной плоскости линзы формируется двумерный фурье-образ сетки — регулярно расположенные по вертикали и по горизонтали световые пятна. Допустим, в фокальной плоскости установлен экран с узкой щелью, через которую проходит только один горизонтальный ряд световых пятен. Тогда из спектра пространственных частот удаляются частоты модуляции светового поля по вертикали, поэтому структура горизонтальных линий сетки в изображении не формируется. В плоскости изображения наблюдаются только вертикальные линии сетки.

Очевидно, что поворотом щели в вертикальное положение можно устранить в изображении сетки вертикальные линии, оставив горизонтальные. Перекрывая горизонтальные ряды пятен интенсивности через один ряд, можно получить удвоение горизонтальных линий в изображении, то есть ложные элементы в изображении. Перекрывание центрального максимума интенсивности приводит к обращению контраста — негативному изображению.

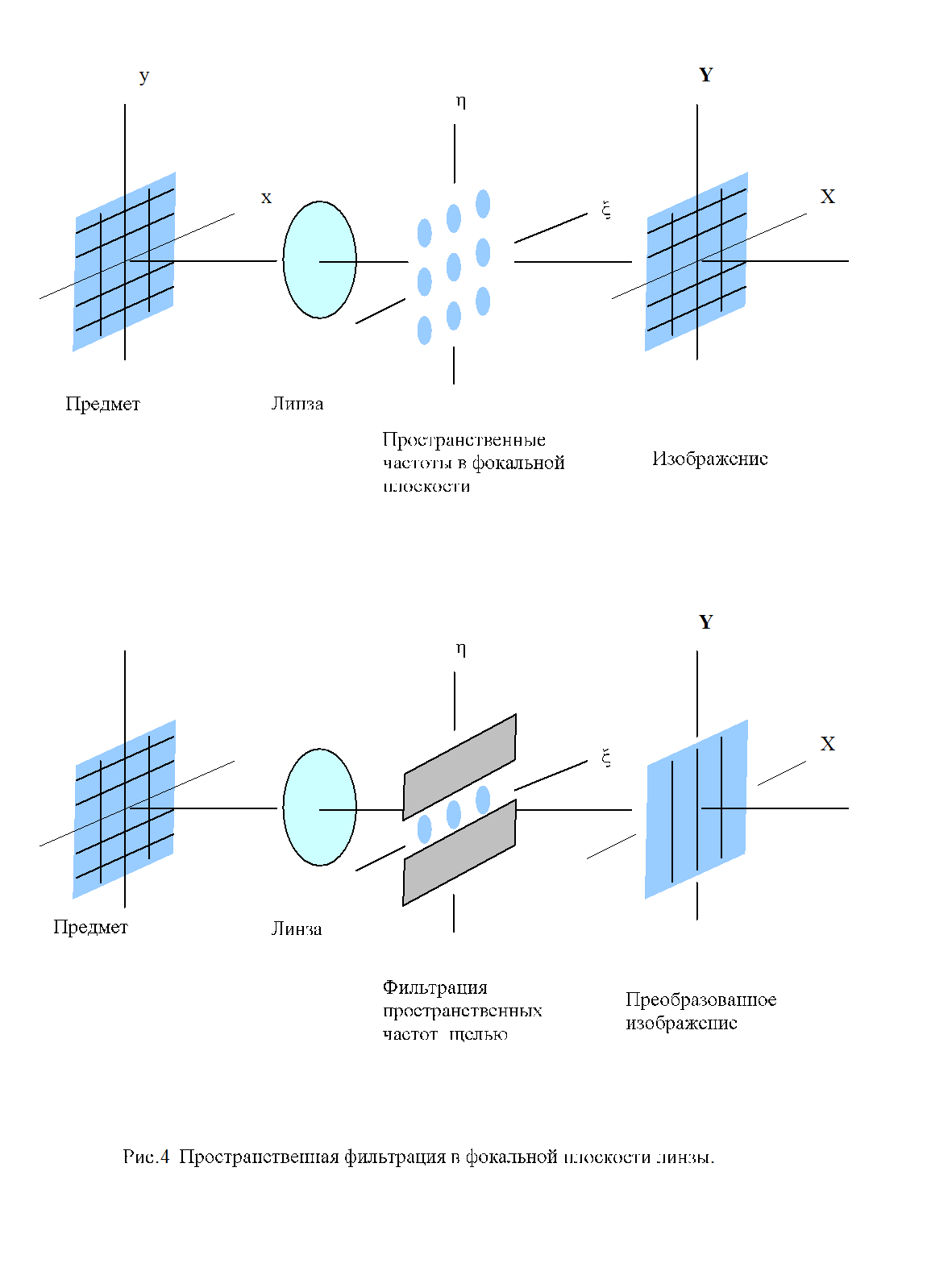
Объект

Фокальная плоскость

Плоскость изображения