
- •§1.1. Уравнения Максвелла.
- •§1.2 Электромагнитные волны в вакууме.
- •Волновое уравнение в вакууме.
- •Комплесксная форма записи.
- •Сферические волны .
- •1.2.6. Энергетические характеристики.
- •2.2 Физика теплового излучение
- •2.2.1 Формула Планка.
- •3.Квантовые представления
- •4.Анализ
- •Физика оптического излучения. Основы физики лазеров.
- •2. Вынужденное (индуцированное) поглощение.
- •3. Вынужденное излучение.
- •Интерференция света Общий закон интерференции
- •Интерференция от двух точечных монохроматических источников
- •Когерентность.
- •II. Пространственная когерентность.
- •Дифракция на прямоугольной апертуре.
- •Дифракция на круглом отверстии.
- •Разрешающая способность телескопа
- •Дифракция Гауссова пучка.
- •4.1. Распространение света в изотропных средах.
- •4.1.3 .Оптические свойства сред в ик, видимой и уф областях спектра.
- •4.2 Распространение немонохроматических волн в изотропных средах.
- •Временное преобразование . Сжатие импульса.
- •4.2 Оптика анизотропных сред.
- •4.2.6. Двойное лучепреломление, построения Гюйгенса для анизотропных сред.
- •4.5 Нелинейная оптика. Оптика сильных световых полей.
- •4.5.1 Исторический обзор.
- •4.5.2 Ангармонический осциллятор. Нелинейная поляризация.
- •Генерация второй гармоники – волновая картина. Условие пространственного синхронизма
- •Получение генерации суммарных и разностных частот
- •Зависимость показателей преломления от интенсивности света
- •Самофокусировка и самодефокусировка света
II. Пространственная когерентность.
Рассмотрим
классическую схему Юнга, источником в
которой является щель шириной
![]() . Выберем узкую полоску щели шириной
. Выберем узкую полоску щели шириной
![]() ,
находящуюся на расстоянии
,
находящуюся на расстоянии
![]() от
оси системы и найдем разность фаз для
волн, идущих от этой полоски.
от
оси системы и найдем разность фаз для
волн, идущих от этой полоски.
О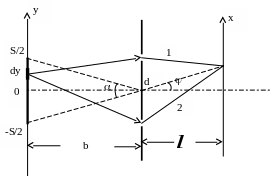 птическая
разность фаз, набираемая волнами 1 и 2 в
области, лежащей за Юнговскими щелями
птическая
разность фаз, набираемая волнами 1 и 2 в
области, лежащей за Юнговскими щелями
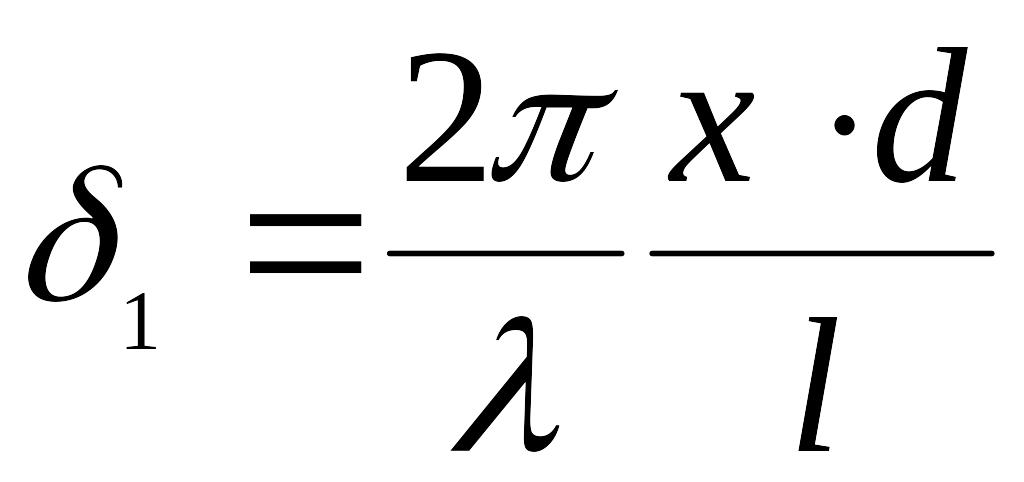 .
(20)
.
(20)
Введем
прекцию среднего вектора
на
ось
![]() ,
с учетом малости угла
,
с учетом малости угла
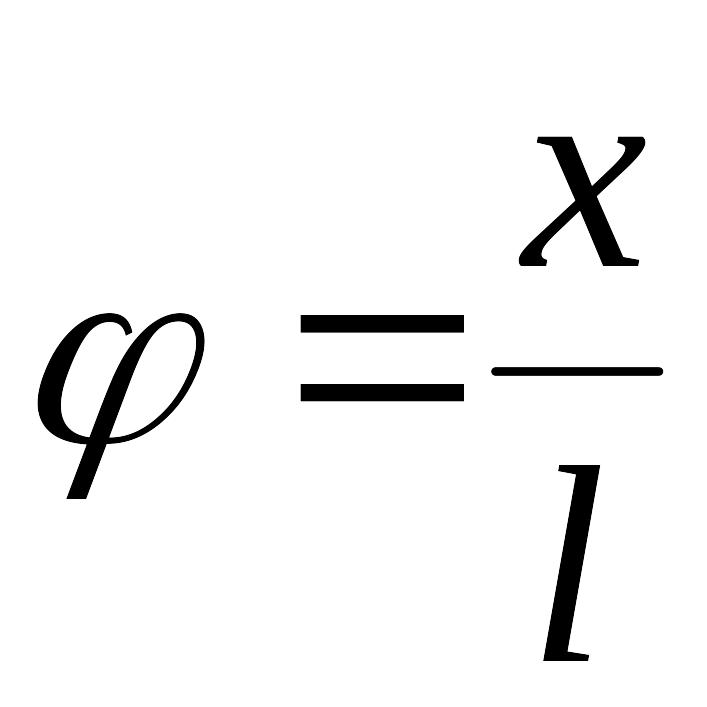 , можно записать
, можно записать
![]() .
(21)
.
(21)
В левой части схемы волны, идущие от точки с координатой набирают дополнительную разность фаз
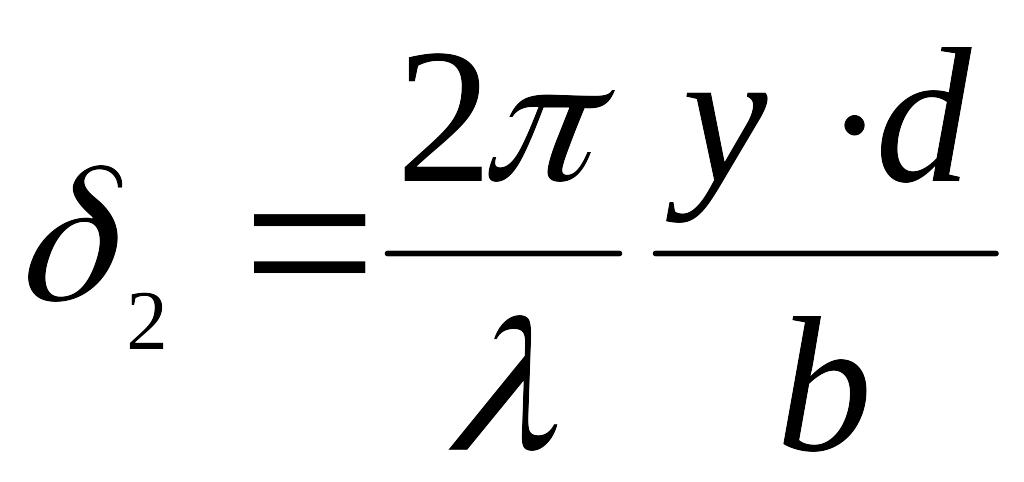 ,
(22)
,
(22)
где
![]() -расстояние
от иточника до экрана с Юнговскими
щелями. Введем прекцию среднего вектора
на
направление
.
Учтем условие
-расстояние
от иточника до экрана с Юнговскими
щелями. Введем прекцию среднего вектора
на
направление
.
Учтем условие
![]() , тогда дополнительную разность фаз
можно представить ввиде
, тогда дополнительную разность фаз
можно представить ввиде
![]() .
(23)
.
(23)
Конечным образом, задача сводится к нахождению суперпозиции интерференционных картин, образующихся при сложении волн, имеющих до падения на Юнговские щели разброс проекций волнового вектора
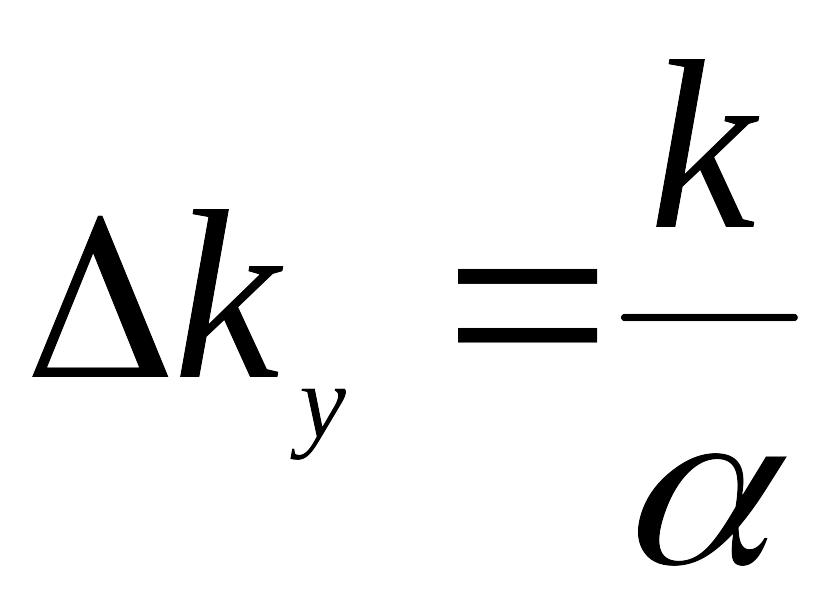 ,
(24)
,
(24)
где -угловой размер источника.
Суммарная разность фаз набираемая в левой и правой частях схемы
![]() (25)
(25)
Нетрудно показать, что интенсивность волн, идущих от бесконечно узкого участка щели , находящегося на расстоянии от центра щели
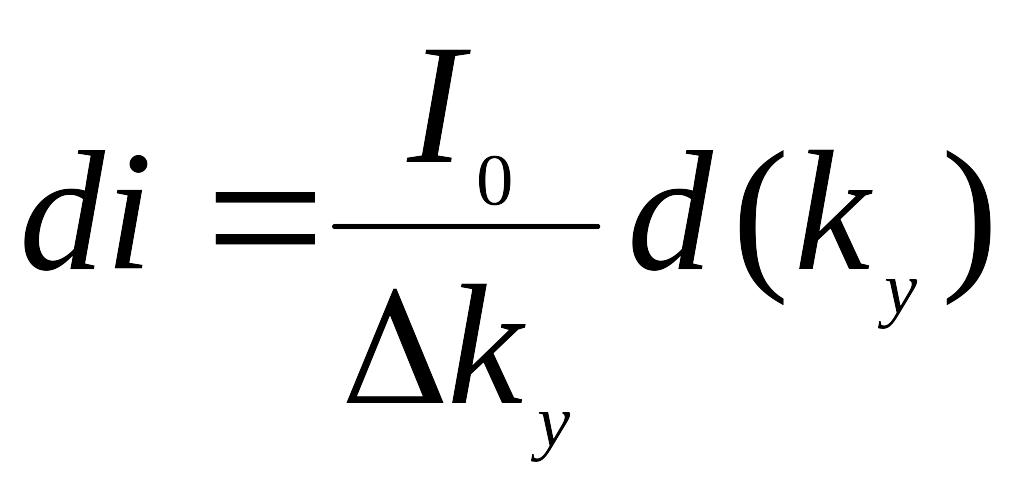 ,
(26)
,
(26)
где -интенсивность света, испускаемого всей щелью.
Полагая, что волны идущие от разных участков щели некогерентны, можем записать выражение для интенсивности интерференционной картртины:
 ,
(27)
,
(27)
или
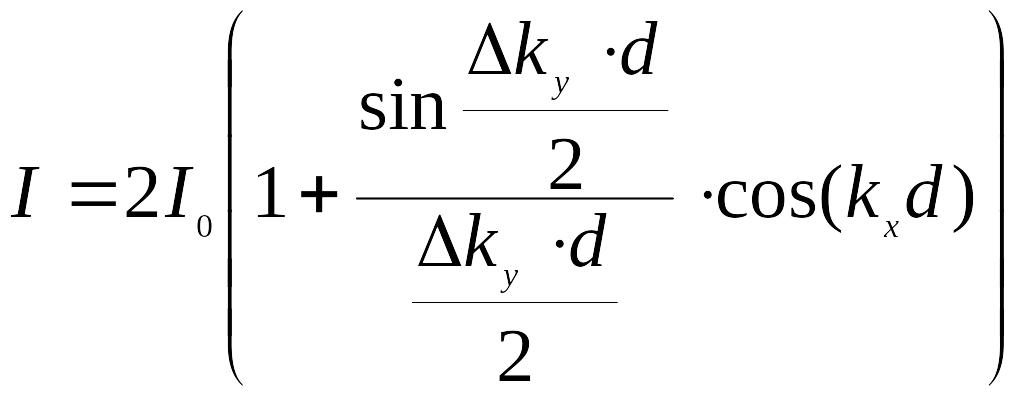 .
(28)
.
(28)
Видность интерференционной картины
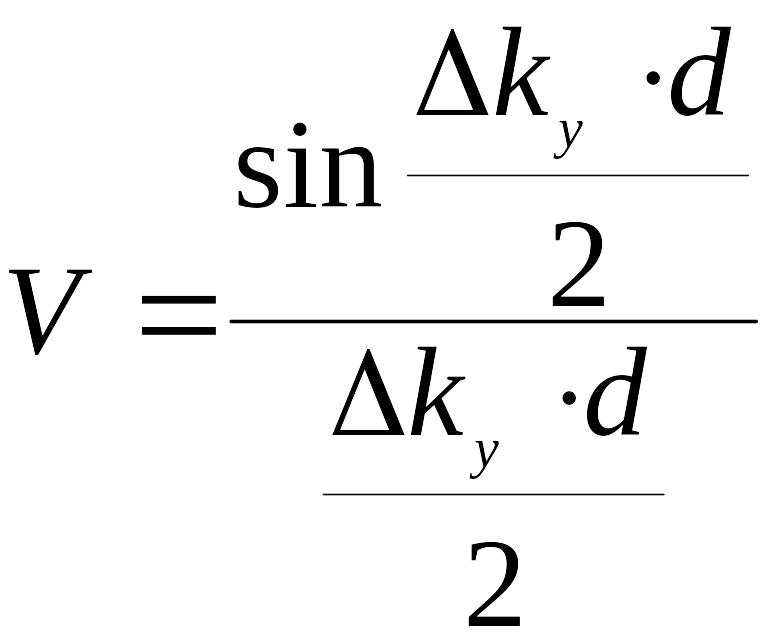 ,
(29)
,
(29)
или
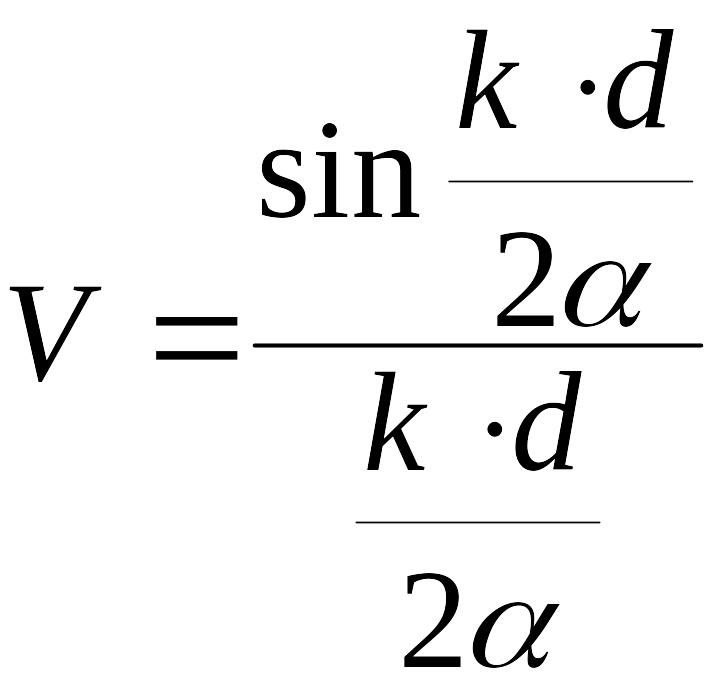 .
(30)
.
(30)
В отличии, от решенной нами задачи о временной когерентности, в данном случае видность интерференционной картины зависит только от параметров источника и расстояния между щелями и не зависит от координаты точки наблюдения. Первое исчезновение интерференционной картины наблюдается при условии
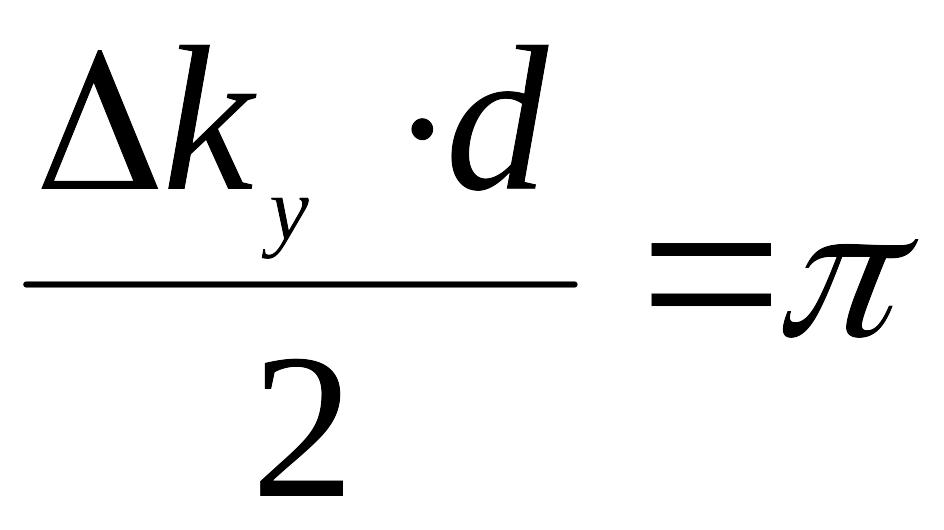 ,
(31)
,
(31)
или
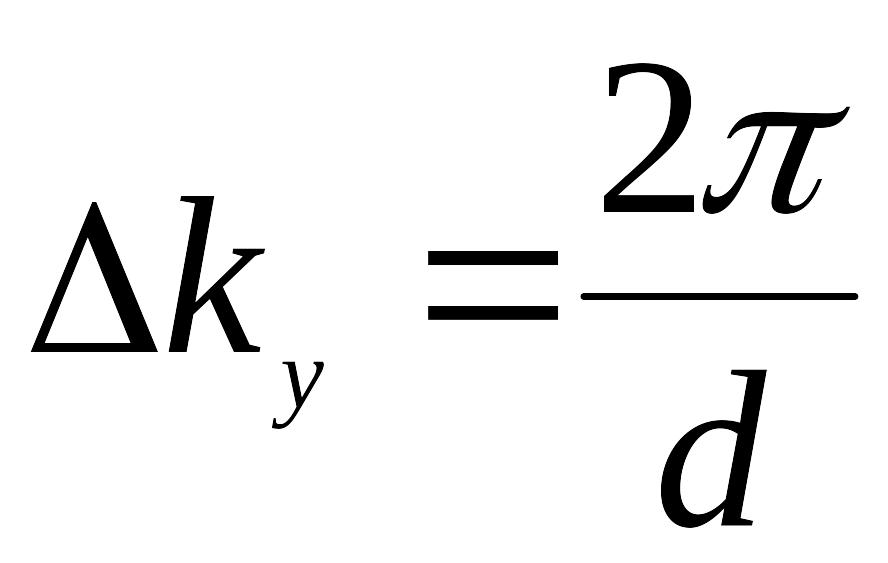 ,
(32)
,
(32)
при этом интерференционная картина исчезает во всем пространстве независимо от координаты .
Для
характеристики степени когерентности
введем параметр
![]() ,
называемый радиусом когерентности.
Величина данного параметра равна
максимальному расстоянию между Юнговскими
щелями при котором еще видна
интерференционная картина, данный
параметр является характеристикой
источника в месте построения
интерференционной схемы. Нетрудно
показать, что
,
называемый радиусом когерентности.
Величина данного параметра равна
максимальному расстоянию между Юнговскими
щелями при котором еще видна
интерференционная картина, данный
параметр является характеристикой
источника в месте построения
интерференционной схемы. Нетрудно
показать, что
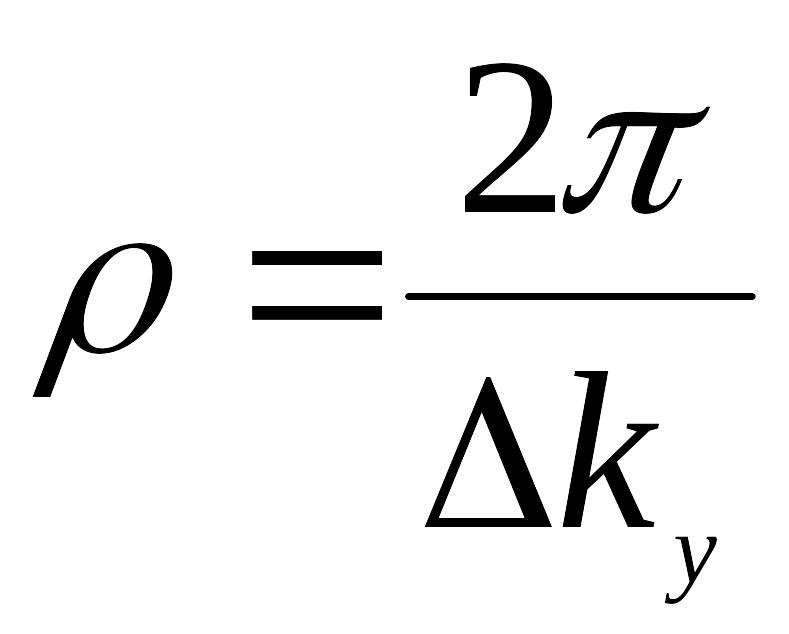 .
(33)
.
(33)
С учетом соотношения (24) получим известное выражение для радиуса когерентности:
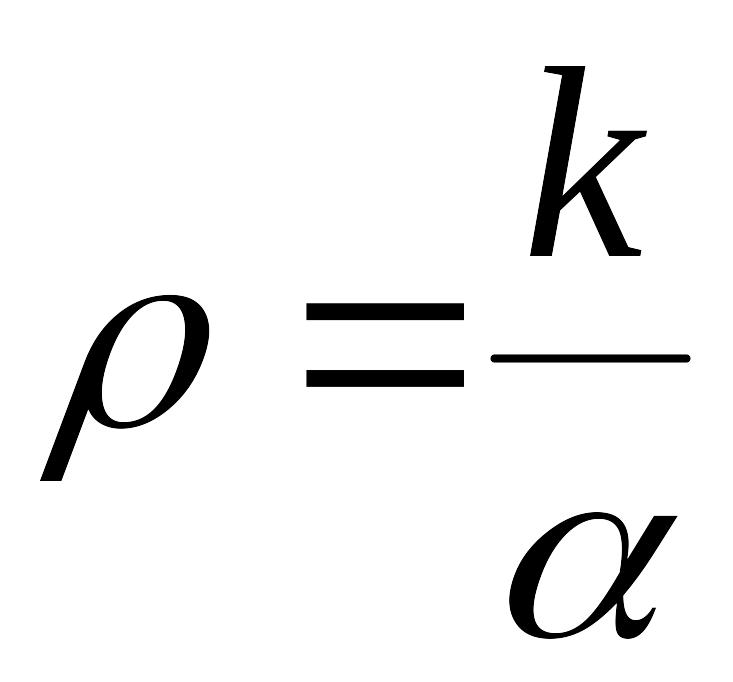 .
(34)
.
(34)
Очевидно,
чем меньше угловой размер источника, и
соответственно разброс прекций волнового
вектора, тем больше радиус когерентности
источника. Можно показать, что волны,
идущие от точек, отстоящих друг от друга
на расстояние
,
имеют разность фаз
![]() и гасят друг друга, чем и объясняется
эффект исчезновения интерференционной
картины.
и гасят друг друга, чем и объясняется
эффект исчезновения интерференционной
картины.
Обычные источники имеют пространственный размер и широкий спектр, поэтому для их характеристики вводится объем когерентности:
![]()
Связь между временными и спектральными характеристиками. Фурье преобразования.
Предположим, что
источник излучения не является
монохроматическим, напряженность
электрического поля такого источника
![]() является функцией частоты
является функцией частоты
![]() .
Выберем бесконечно узкий спектральный
интервал
.
Выберем бесконечно узкий спектральный
интервал
![]() в пределах которого можем считать волну
монохроматической, тогда поле такого
элементарного источника может быть
записано следующим образом:
в пределах которого можем считать волну
монохроматической, тогда поле такого
элементарного источника может быть
записано следующим образом:
![]() .
(1)
.
(1)
Результирующее поле такого источника
![]() ,
(2)
,
(2)
здесь
![]() -нормировочный
множитель.
-нормировочный
множитель.
 Выражение
(2) показывает, что функция
Выражение
(2) показывает, что функция
![]() ,
описывающая временной характер поля
источника и функция
,
описывающая временной характер поля
источника и функция
![]() ,
описывающая его спектральный состав,
связаны Фурье преобразованием. Из
выражения (2) с помощью обратного Фурье
преобразования можно найти спектральную
амплитуду
,
описывающая его спектральный состав,
связаны Фурье преобразованием. Из
выражения (2) с помощью обратного Фурье
преобразования можно найти спектральную
амплитуду
![]() .
(3)
.
(3)
Найдем интенсивность источника сложного спектрального состава,
Для
этого запишем выражение для нахождения
интенсивности
![]() в явном виде:
в явном виде:
![]() ,
(4)
,
(4)
где T- время наблюдения.
Подставив в выражение (4) в виде (2), поменяв порядок интегрирования, можно получить для интенсивности следующее выражение
![]() .
(5)
.
(5)
Очевидно, что функция
![]() (6)
(6)
является спектральной плотностью интенсивности и интенсивность источника может быть записана в виде
![]() .
(7)
.
(7)
Р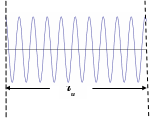 ассмотрим
спектр цуга
ассмотрим
спектр цуга
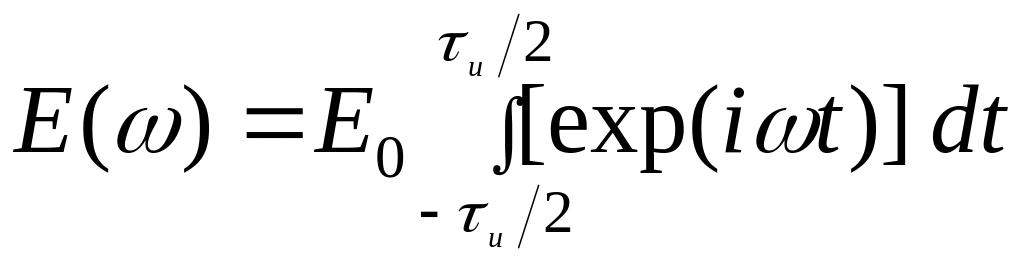
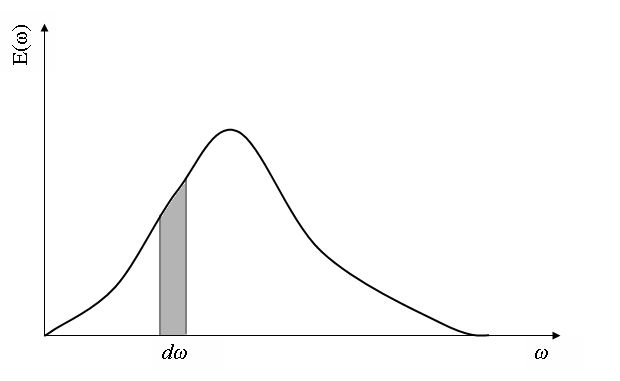
Несложные вычисления дают следующее выражение для спектра.
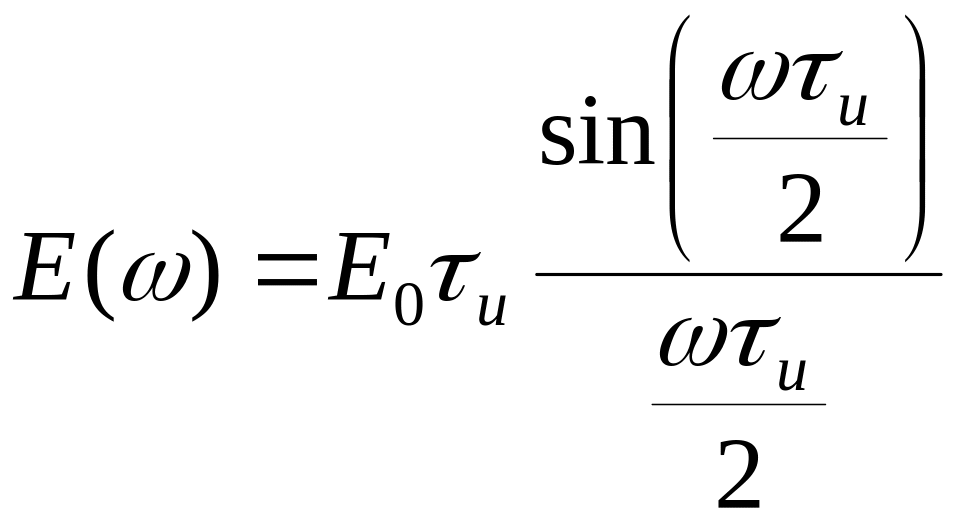
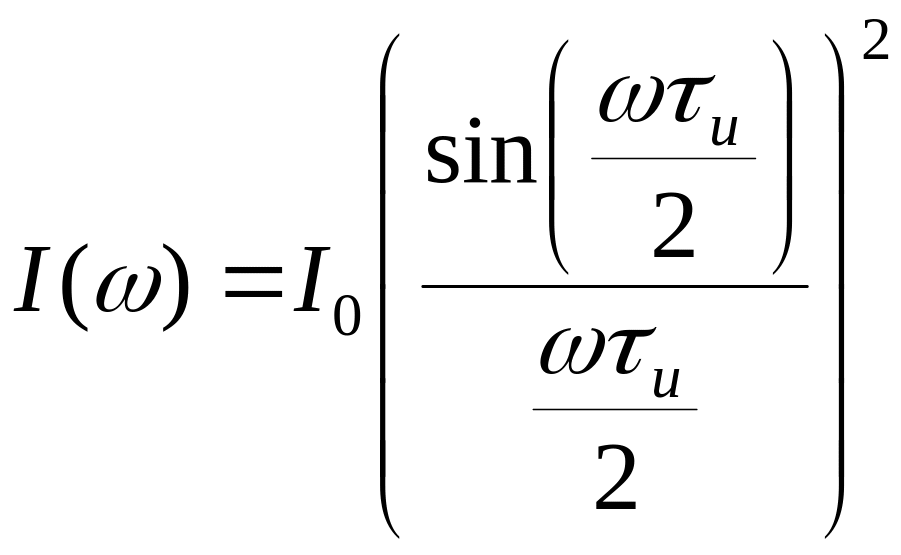
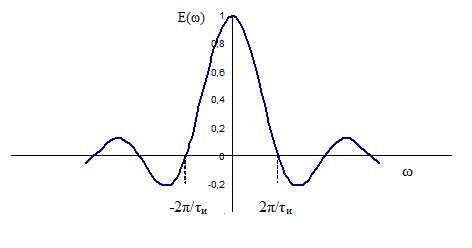
Распределение напряженности в спектре цуга
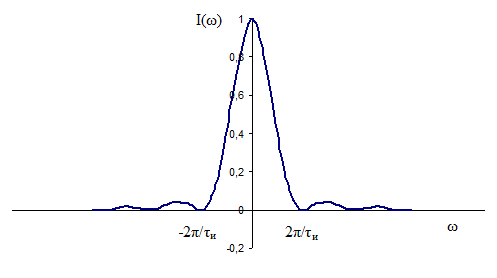
Распределение интенсивности в спектре цуга.
Ширина спектра определяется условием:
![]() ,
отсюда ширина
спектра
,
отсюда ширина
спектра
![]() или
или
![]()
Лекция 10. Пространственная когерентность.
Рассмотрим классическую схему Юнга, источником в которой является щель шириной . Выберем узкую полоску щели шириной , находящуюся на расстоянии от оси системы и найдем разность фаз для волн, идущих от этой полоски.
О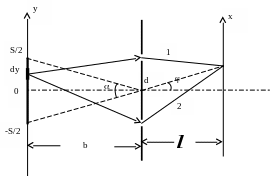 птическая
разность фаз, набираемая волнами 1 и 2 в
области, лежащей за Юнговскими щелями
птическая
разность фаз, набираемая волнами 1 и 2 в
области, лежащей за Юнговскими щелями
. (1)
.
В левой части схемы волны, идущие от точки с координатой набирают дополнительную разность фаз
, (2)
где -расстояние от иточника до экрана с Юнговскими щелями.
Суммарная
разность фаз
![]()
Конечным образом, задача сводится к нахождению суперпозиции интерференционных картин, образующихся при сложении волн, идущих от разных некогерентных частей источника.
Интенсивность
волн, идущих от бесконечно узкого участка
щели
,
находящегося на расстоянии
от
центра щели
![]() .
.
Элементарная интенсивность
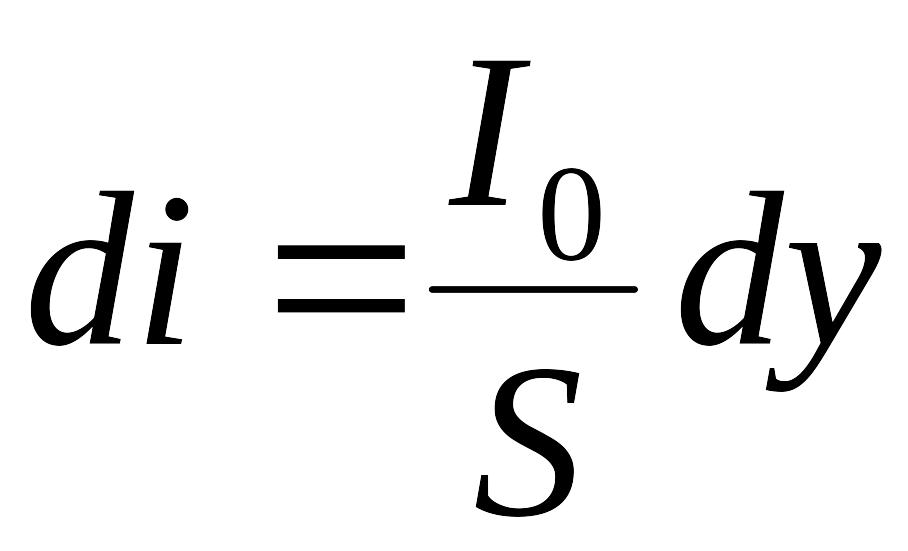 ,
(3)
,
(3)
где -интенсивность света, испускаемого всей щелью.
Полагая, что волны идущие от разных участков щели некогерентны, можем записать выражение для интенсивности интерференционной картртины:
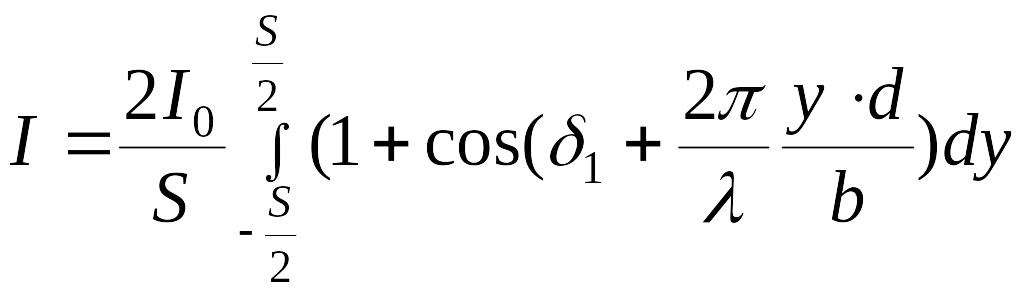 .
(4)
.
(4)
Выполнив интегрирование получим
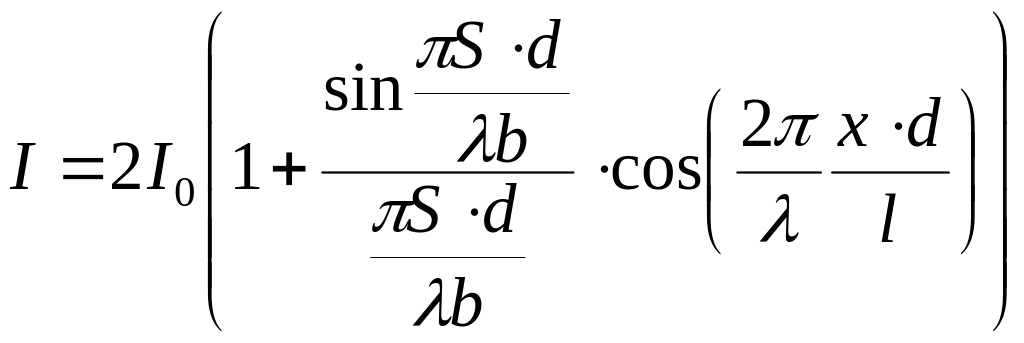
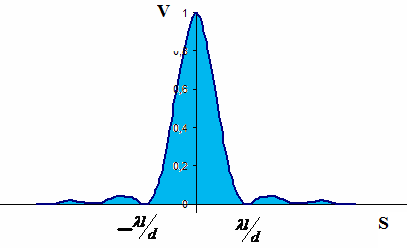
Видность интерференционной картины
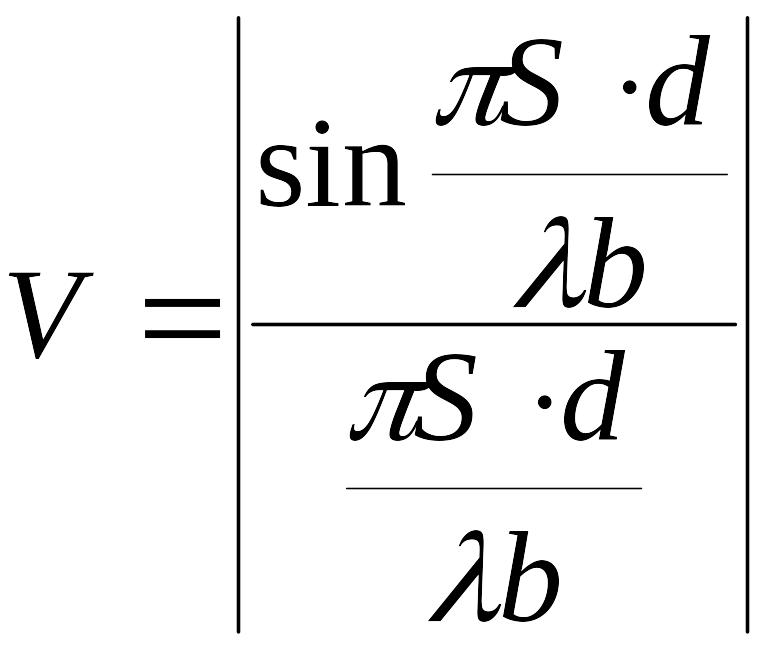 ,
(4)
,
(4)
.
В отличии, от решенной нами задачи о временной когерентности, в данном случае видность интерференционной картины зависит только от параметров источника и расстояния между щелями и не зависит от координаты точки наблюдения. Первое исчезновение интерференционной картины наблюдается при условии
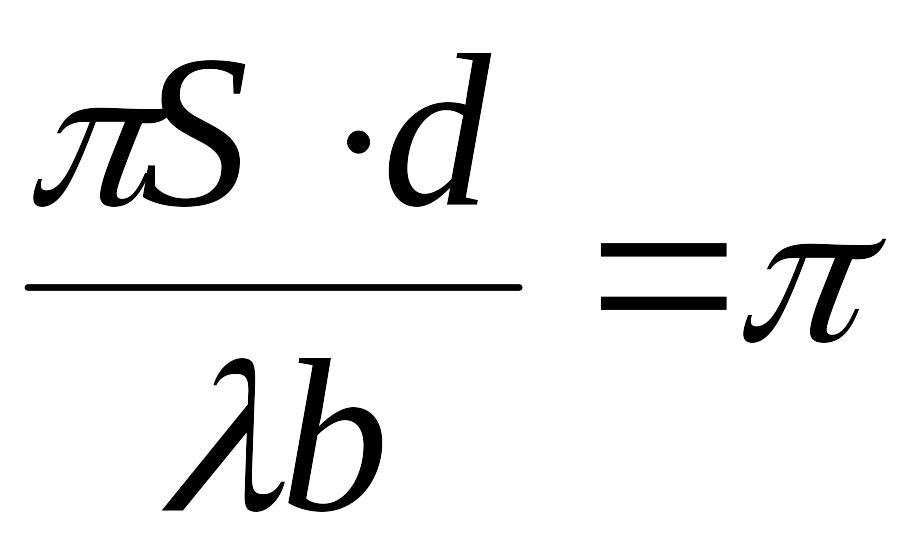 ,
(5)
,
(5)
или при ширине щели
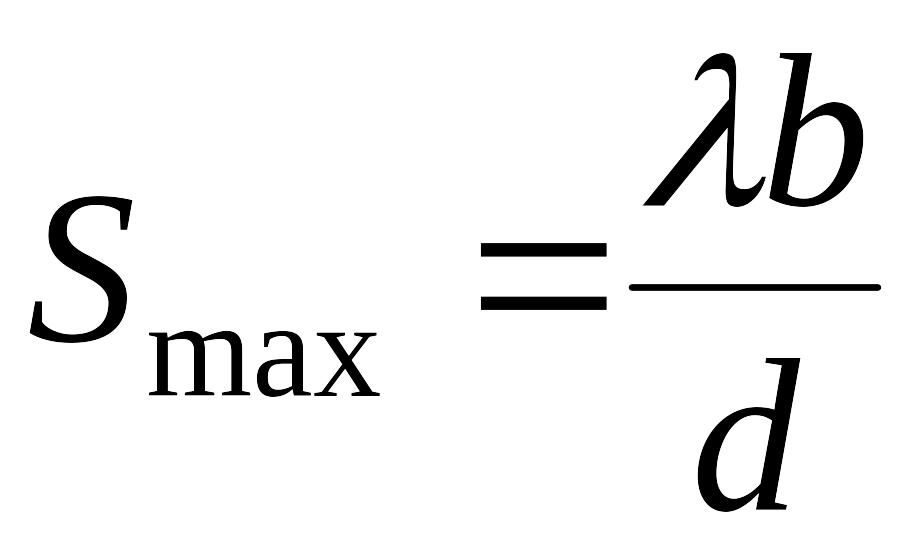 ,
(6)
,
(6)
при этом интерференционная картина исчезает во всем пространстве независимо от координаты .
Оценки
и цифры:
![]() .
.
Поэтому все спектральные приборы оснащены щелевыми механизмами, позваляющими регулировать ширину входной и выходной щелей с точностью до тысячной доли милиметра.
Д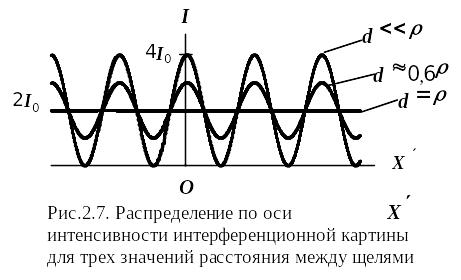 ля
характеристики степени когерентности
введем параметр
,
называемый радиусом когерентности.
Величина данного параметра равна
максимальному расстоянию между Юнговскими
щелями при котором еще видна
интерференционная картина, данный
параметр является характеристикой
источника в месте построения
интерференционной схемы. Нетрудно
показать, что при заданном размере
источника
ля
характеристики степени когерентности
введем параметр
,
называемый радиусом когерентности.
Величина данного параметра равна
максимальному расстоянию между Юнговскими
щелями при котором еще видна
интерференционная картина, данный
параметр является характеристикой
источника в месте построения
интерференционной схемы. Нетрудно
показать, что при заданном размере
источника
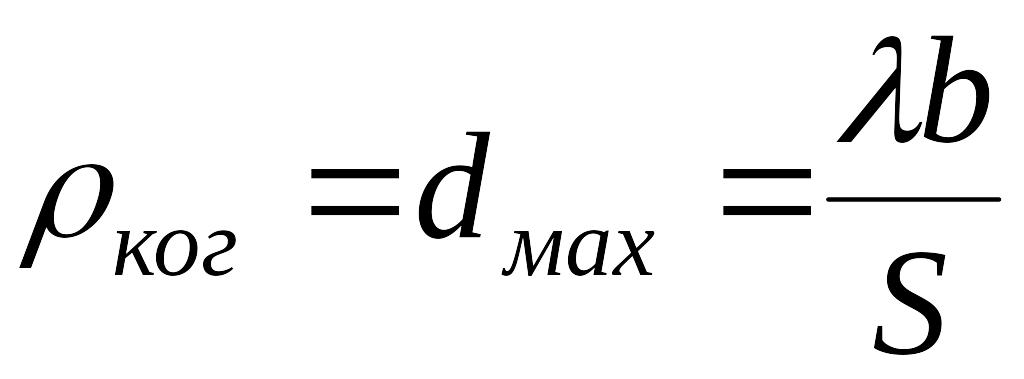 .
(7)
.
(7)
Учтя,
что угловой размер источника
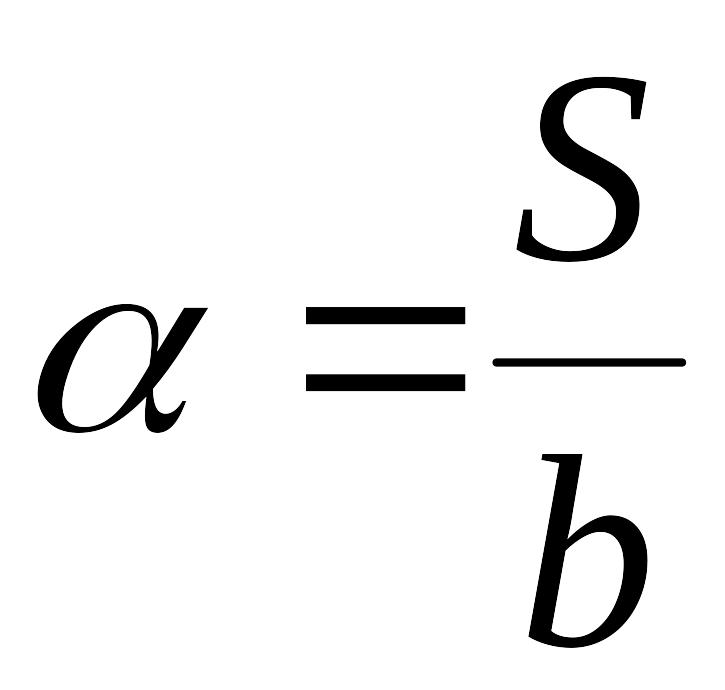 получим известное выражение для радиуса
когерентности:
получим известное выражение для радиуса
когерентности:
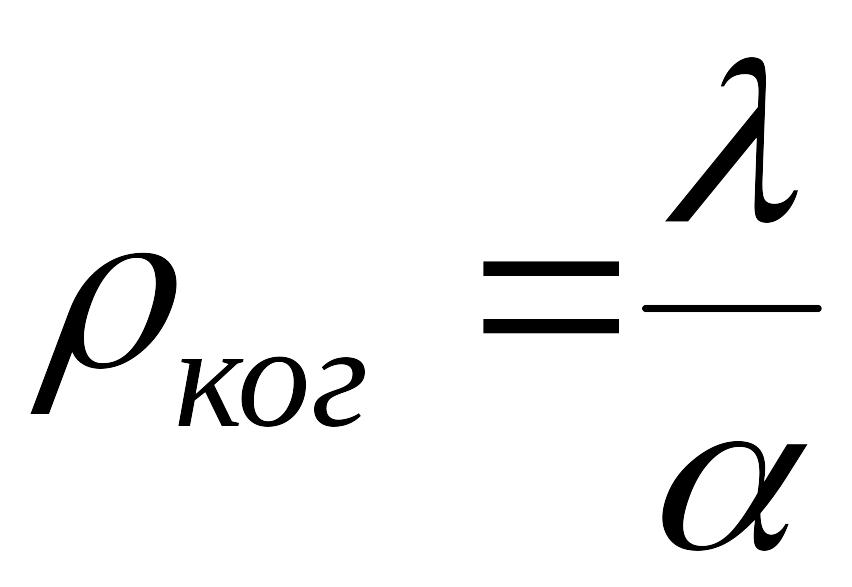 .
(8)
.
(8)
Очевидно, чем меньше угловой размер источника, тем больше радиус когерентности источника. Можно показать, что волны, идущие от точек, отстоящих друг от друга на расстояние , имеют разность фаз и гасят друг друга, чем и объясняется эффект исчезновения интерференционной картины.
Обычные источники имеют пространственный размер и широкий спектр, поэтому для их характеристики вводится объем когерентности:
(9)
Многолучевая интерференция.
Рассмотрим теперь
интерференционную картину от
![]() когерентных источников для случая,
когда фаза
когерентных источников для случая,
когда фаза
![]() -го
источника отличается от фазы первого
источника на величину
-го
источника отличается от фазы первого
источника на величину
![]() ,
где
- разность фаз между соседними источниками.
Согласно принципу суперпозиции
комплексная амплитуда суммарного
волнового поля этих источников
определяется выражением для суммы
членов геометрической прогрессии
,
где
- разность фаз между соседними источниками.
Согласно принципу суперпозиции
комплексная амплитуда суммарного
волнового поля этих источников
определяется выражением для суммы
членов геометрической прогрессии
![]()
Амплитуда
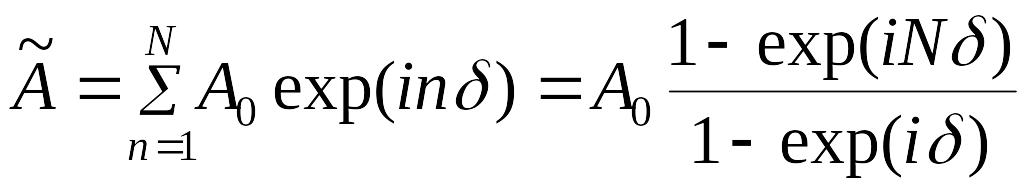
В соответствии с формулой (2.1), после преобразований получаем формулу для интенсивности
 ,
(10)
,
(10)
где
![]() - интенсивность света, испускаемого
одним источником.
- интенсивность света, испускаемого
одним источником.
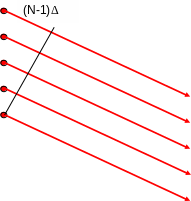 В частности, когда источники расположены
на отрезке прямой на равном расстоянии
друг от друга, выражение для разности
фаз имеет вид:
В частности, когда источники расположены
на отрезке прямой на равном расстоянии
друг от друга, выражение для разности
фаз имеет вид:
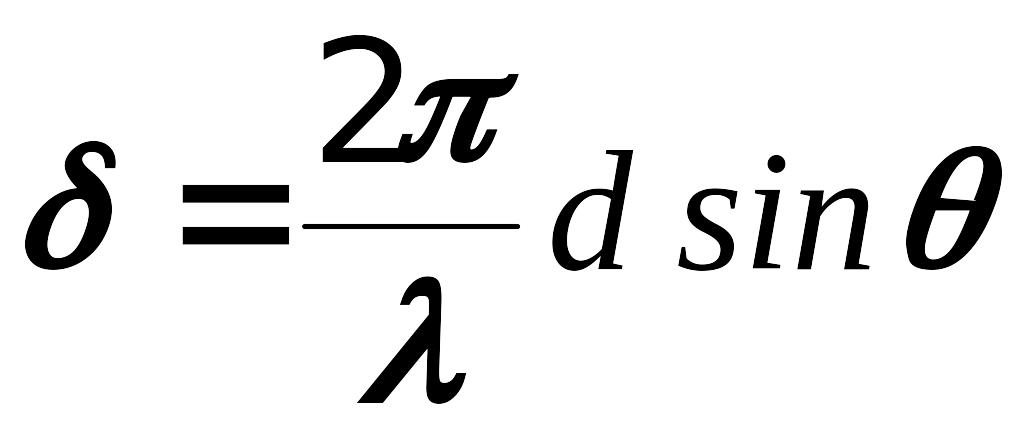 .
(11)
.
(11)
Из формулы (10) легко
показать, что интенсивность излучения
для углов, удовлетворяющих условию
![]() ,
или
,
или
![]() (12)
(12)
оказывается в
![]() больше
интенсивности одного источника
,
т.е. в этих направлениях наблюдаются
(главные) максимумы излучения.
больше
интенсивности одного источника
,
т.е. в этих направлениях наблюдаются
(главные) максимумы излучения.
Интерференционные минимумы определяются равенством 0 только числителя при не равном 0 знаменателе в выражении (2). Условия минимума:
![]() или
или
![]() ,
где
,
где
![]() ,
то есть между главными максимумами
наблюдается
,
то есть между главными максимумами
наблюдается
![]() -минимум.
-минимум.
И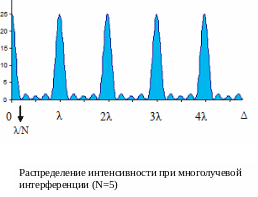 нтенсивность
в максимуме интеренции увеличивается
нтенсивность
в максимуме интеренции увеличивается
![]() раз,
ширина максимума уменьшается в
раз,
что позволяет использовать многолучевую
интерференции для наблюдения узких
спектральных линий. На основе данного
явления работают многолучевые
интерферометры и дифракционные решетки.
раз,
ширина максимума уменьшается в
раз,
что позволяет использовать многолучевую
интерференции для наблюдения узких
спектральных линий. На основе данного
явления работают многолучевые
интерферометры и дифракционные решетки.
ЛЕКЦИЯ 11.
ДИФРАКЦИЯ
Дифракция Френеля. Метод зон Френеля.
Определение Зоммерфельда.
Дифракцией света называется совокупность явлений, возникающих при распространении ограниченного пучка света, заключающихся в огибании границ, определенных законами геометрической оптики. При этом в области дифракции наблюдается периодическое распределение интенсивности дифрагировавших волн с максимумами и минимумами освещенности.
Явление дифракции наблюдается как для волн, проходящих различные диафрагмы: щели, отверстия различной формы и т.д., так и для волн, отраженных от различных объектов.
Под дифракцией мы будем понимать совокупность явлений, возникающих при распространении световой волны, пространственно модулированной по амплитуде или фазе. В частности, дифракция возникает при распространении волнового фронта, ограниченного с помощью экранов различного вида (амплитудная модуляция), или при прохождении фронтом ограниченной прозрачной пластинки (фазовая модуляция). С этой точки зрения построение изображения объекта также относится к задачам дифракции.
Дифракция Френеля. Метод зон Френеля.
В общем случае для построения изображения необходимо найти решение волнового уравнения с граничными условиями, определяемыми геометрией и характеристиками объекта. Получить такое решение сложно даже для объектов простейшей формы, поэтому в оптике используют приближенные методы решения, основанные на том, что длина световой волны обычно мала по сравнению с характерными масштабами задачи: размером объекта и расстоянием до точки наблюдения. Одним из таких методов построения изображения объекта, как было показано Кирхгофом, является метод, основанный на принципе Гюйгенса-Френеля.
Согласно этому принципу световое поле, возникающее вследствие дифракции на некотором объекте, представляет собой картину интерференции сферических волн, излучаемых вторичными элементарными источниками. При этом предполагается, что амплитуда поля вторичных источников на закрытой объектом части волнового фронта равна нулю, а на открытой части фронта – амплитуде исходного поля, т.е. пренебрегается эффектами вблизи его краев объекта (граничное условие Кирхгофа).
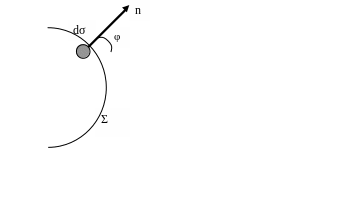
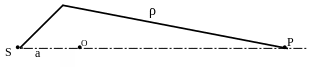
В соответствии с принципом Гюйгенса-Френеля суммирование вторичных волн в произвольной точке наблюдения P производится с помощью интеграла Гюйгенса-Френеля, который имеет вид:
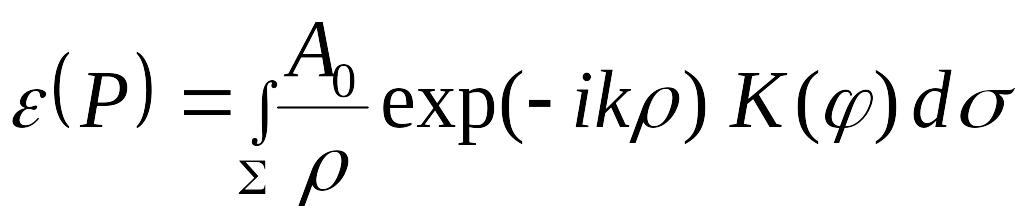 .
(3.1)
.
(3.1)
Здесь
![]() и
А0,
соответственно, амплитуды суммарного
волнового поля в точке наблюдения Р
и поля элементарного вторичного источника
площадью
и
А0,
соответственно, амплитуды суммарного
волнового поля в точке наблюдения Р
и поля элементарного вторичного источника
площадью
![]() ,
расположенного в произвольной точке
волнового фронта падающей волны; второй
множитель в подынтегральном выражении
описывает пространственную часть
сферической волны, излучаемой элементарным
источником, а множитель
,
расположенного в произвольной точке
волнового фронта падающей волны; второй
множитель в подынтегральном выражении
описывает пространственную часть
сферической волны, излучаемой элементарным
источником, а множитель
![]() учитывает, что вклад элемента
в суммарное поле зависит от угла
учитывает, что вклад элемента
в суммарное поле зависит от угла
![]() между нормалью к площади элемента и
направлением радиус - вектора
между нормалью к площади элемента и
направлением радиус - вектора
![]() в точку наблюдения (см. рис.):
в точку наблюдения (см. рис.):
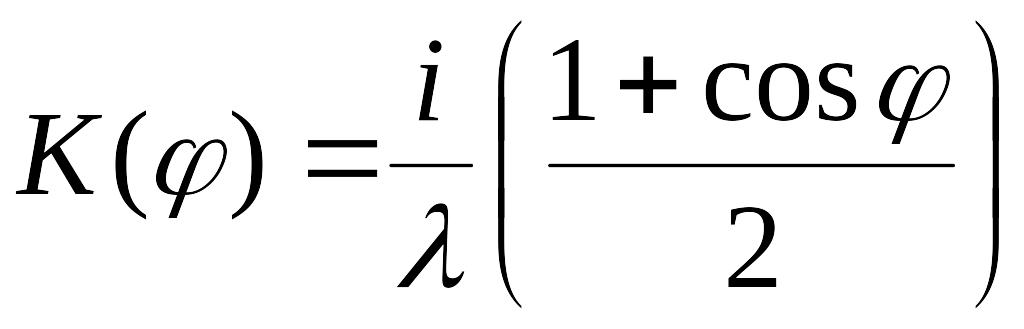 .
.
Качественно можно
рассмотреть дифракционную картину с
помощью метода зон Френеля. В соответствии
с принципом Гюйгенса-Френеля, любая
точка пространства, до которой дошел
волновой фронт, становится источником
вторичных волн. Дифракционная картина
является результатом интерференции
этих волн. Пусть в точке
расположен источник света (рис.). Волна,
распространяющаяся от источника, имеет
сферический волновой фронт радиуса
![]() .
Рассмотрим точку
,
находящуюся от волнового фронта на
расстоянии
.
.
Рассмотрим точку
,
находящуюся от волнового фронта на
расстоянии
.
С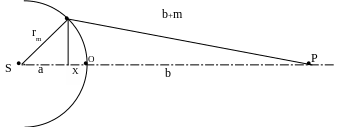 огласно
Френелю, волновой фронт разбивается на
зоны, при этом расстояние до точки
увеличивается при переходе к следующей
зоне на
огласно
Френелю, волновой фронт разбивается на
зоны, при этом расстояние до точки
увеличивается при переходе к следующей
зоне на
![]() .
На рисунке
.
На рисунке
![]() радиус
- ой зоны Френеля. Расстояние от края
радиус
- ой зоны Френеля. Расстояние от края
![]() ой
зоны до точки
равно
ой
зоны до точки
равно
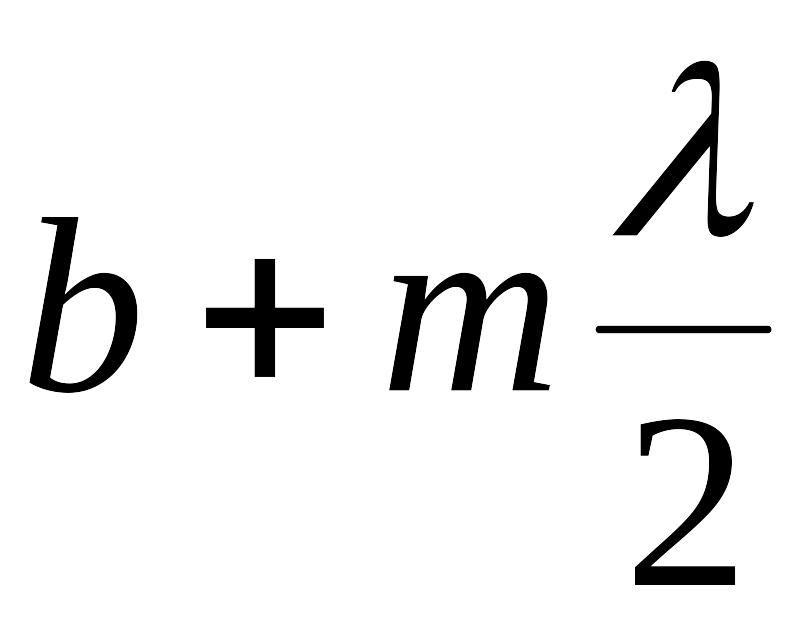 .
.
Нетрудно показать, с учетом оптического приближения λ<<b, что
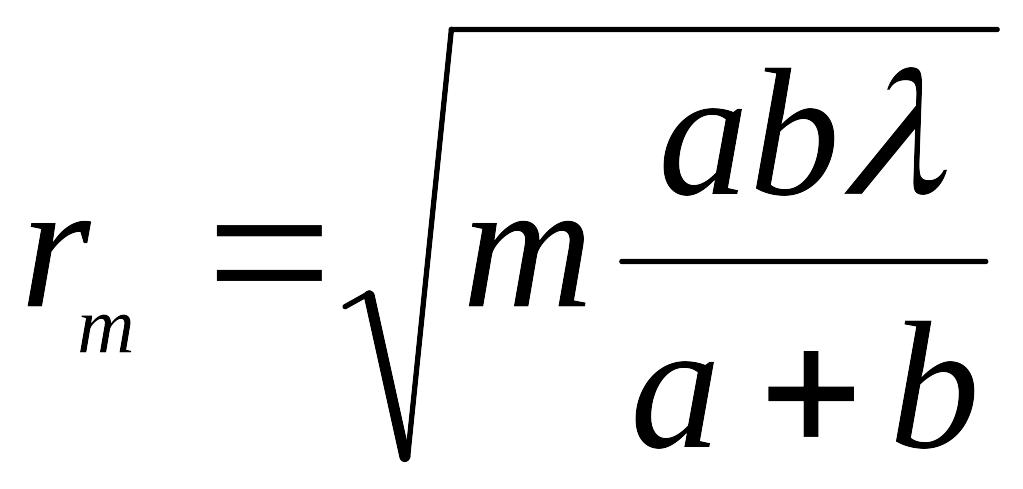 . (41)
. (41)
Так как разность
хода от соседних зон составляет
,
волны, попадающие от них в точку
,
гасят друг друга. Поэтому в точке
наблюдается максимум, если открыто
нечетное число зон Френеля, и минимум,
если открыто четное число зон Френеля
для точки
.
Если на круглое отверстие падает плоская
волна,
![]() .
Формула (41) упрощается.
.
Формула (41) упрощается.
![]() (42)
(42)
Рассмотрим следующую задачу. Перекроем волновой фронт экраном с открывающейся диафрагмой, увеличивая радиус отверстия, будем наблюдать за изменением амплитуды в точке (Р). Разобьем зоны Френеля на бесконечно тонкие слои и построим результирующую амплитуду. Полученная линия называется спиралью Френеля. При полностью открытом волновом фронте амплитуда равна А0.
З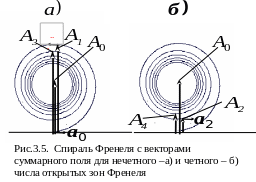 онная
пластинка.
онная
пластинка.
Линза таутохронная система.
Границы применимости зонной теории Френеля.
Рассмотрим более подробно распространение ограниченного пучка света.
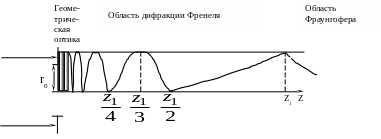
Пусть плоская
монохроматическая световая волна падает
на отверстие радиуса
![]() .
Рассмотрим, как будет меняться
интенсивность света для точек,
расположенных вдоль оси
.
Найдем точку, для которой отверстие
будет представлять одну зону Френеля.
.
Рассмотрим, как будет меняться
интенсивность света для точек,
расположенных вдоль оси
.
Найдем точку, для которой отверстие
будет представлять одну зону Френеля.
В формуле (42)
положим
![]() ;
;
![]() ;
;
![]() ,
тогда
,
тогда
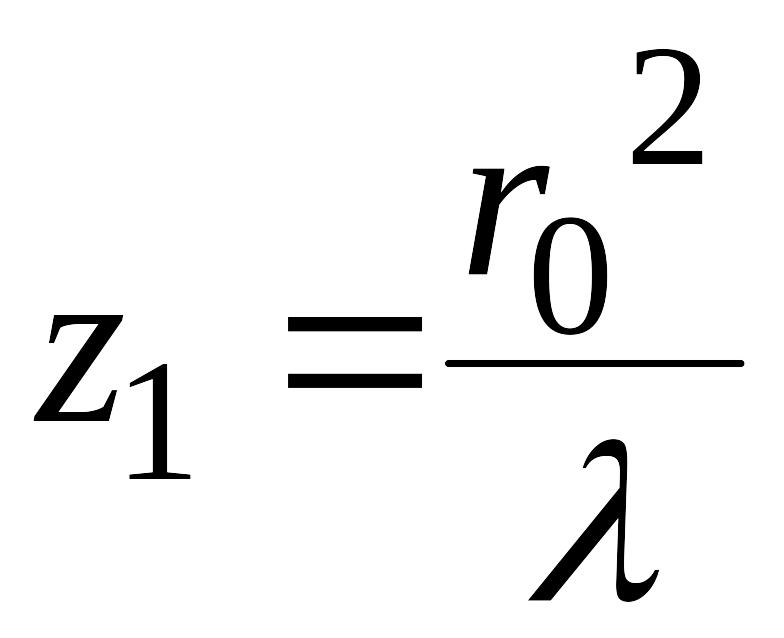 , (43)
, (43)
в этой точке наблюдается максимум.
При
![]()
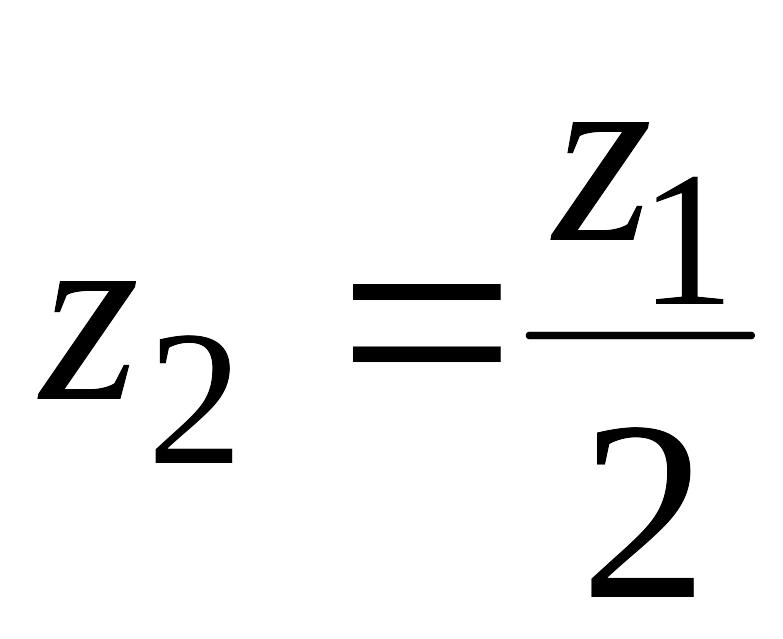 (44)
(44)
в точке наблюдается минимум.
Следующий максимум будет при
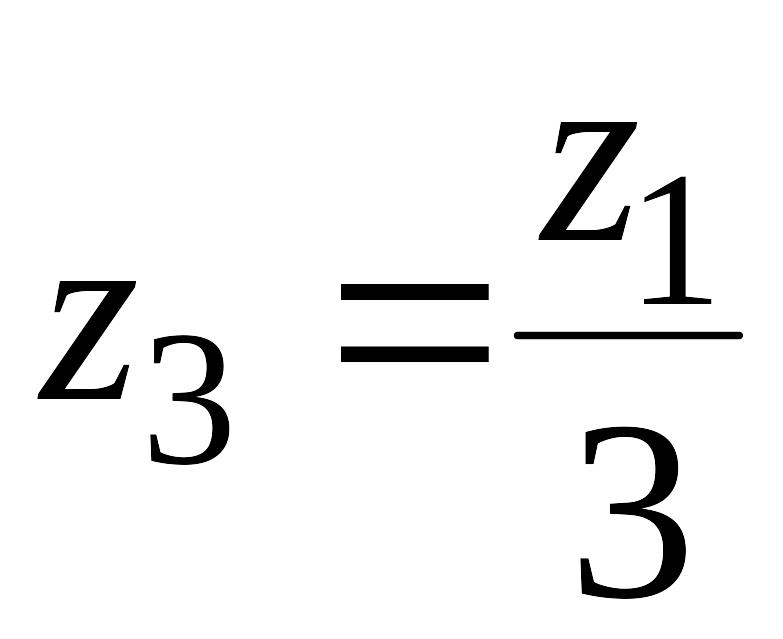 (45)
(45)
и т.д.
Максимумы будут
сближаться, и при
<<
![]() мы перейдем в область геометрической
оптики. При этом соседние максимумы уже
не будут различимы.
мы перейдем в область геометрической
оптики. При этом соседние максимумы уже
не будут различимы.
Если мы будет
продвигаться по оси
вправо, удаляясь от отверстия радиусом
за точку
![]() ,
отверстие для данной области будет
представлять собой часть первой зоны
Френеля и интенсивность световой волны
будет падать ~
,
отверстие для данной области будет
представлять собой часть первой зоны
Френеля и интенсивность световой волны
будет падать ~
![]() .
То есть для области
>
волна будет представлять собой сферическую
волну независимо от формы объекта.
Данная область называется областью
дифракции Фраунгофера.
.
То есть для области
>
волна будет представлять собой сферическую
волну независимо от формы объекта.
Данная область называется областью
дифракции Фраунгофера.
Зоны Шустера. Дифракция на краю экрана.
Полная амплитуда
светового поля в точке наблюдения в
соответствии с (3.5) найдется как сумма
этих элементарных векторов, причем
интегрирование ведется фактически по
открываемой щелью части светового
фронта, т.е. в пределах отрезка
![]() .
.
В силу симметрии
картины относительно оси Z
рассмотрим сначала только вклад от
верхней половины щели, где
![]() При “бесконечно” малой ширине щели
она открывает на падающем световом
фронте элемент
При “бесконечно” малой ширине щели
она открывает на падающем световом
фронте элемент
![]() ,
лежащий на оси Z
(см. рис.3.2), для которого
,
лежащий на оси Z
(см. рис.3.2), для которого
![]() ,
и фаза соответствующего элементарного
вектора колебаний светового поля
,
и фаза соответствующего элементарного
вектора колебаний светового поля
![]() также близка к нулю, т. е. этот вектор
направлен вдоль действительной оси. С
увеличением ширины щели
также близка к нулю, т. е. этот вектор
направлен вдоль действительной оси. С
увеличением ширины щели
![]() для
вновь открываемых элементов светового
фронта возрастает длина оптического
пути до точки наблюдения и, следовательно,
возрастает сдвиг фаз относительно
элемента
.
Поэтому вектора, представляющие колебания
светового поля этих элементов,
поворачиваются относительно действительной
оси. Если ширина щели такова, что между
волнами, идущими от крайнего (
для
вновь открываемых элементов светового
фронта возрастает длина оптического
пути до точки наблюдения и, следовательно,
возрастает сдвиг фаз относительно
элемента
.
Поэтому вектора, представляющие колебания
светового поля этих элементов,
поворачиваются относительно действительной
оси. Если ширина щели такова, что между
волнами, идущими от крайнего (![]() )
и ц
)
и ц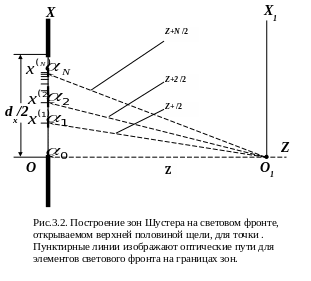 ентрального
(
)
элементов открытой части волнового
фронта до точки
ентрального
(
)
элементов открытой части волнового
фронта до точки
![]() ,
набирается разность хода
,
набирается разность хода
![]() ,
вектор колебаний светового поля элемента
поворачивается на
,
вектор колебаний светового поля элемента
поворачивается на
![]() .
Согласно
формуле (3.5) это соответствует полуширине
щели
.
Согласно
формуле (3.5) это соответствует полуширине
щели
![]() ,
а щель открывает на световом фронте
полосу, называемую первой зоной
Шустера. При
увеличении ширины щели до размера, при
котором оптическая разность хода волн,
идущих от крайнего
,
а щель открывает на световом фронте
полосу, называемую первой зоной
Шустера. При
увеличении ширины щели до размера, при
котором оптическая разность хода волн,
идущих от крайнего
![]() и
центрального элементов открытого
фронта, возрастает до
и
центрального элементов открытого
фронта, возрастает до
![]() ,
вектор колебаний светового поля элемента
поворачивается
на
,
вектор колебаний светового поля элемента
поворачивается
на
![]() .
Согласно
формуле (3.5) это соответствует полуширине
щели
.
Согласно
формуле (3.5) это соответствует полуширине
щели
![]() ,
а щель открывает на световом фронте
полосу, называемую второй зоной
Шустера.
Далее длина оптического пути для
открываемого крайнего элемента светового
фронта возрастает последовательно, на
,
а щель открывает на световом фронте
полосу, называемую второй зоной
Шустера.
Далее длина оптического пути для
открываемого крайнего элемента светового
фронта возрастает последовательно, на
![]() .
Сдвиг фазы при этом также возрастает,
проходя, соответственно, значения 3
,
4
.
Сдвиг фазы при этом также возрастает,
проходя, соответственно, значения 3
,
4![]() ,
… N
,
и т. д., а вектор колебаний светового
поля поворачивается на эти углы. Согласно
формуле (3.5) поворот вектора происходит
при полуширине щели равной
,
… N
,
и т. д., а вектор колебаний светового
поля поворачивается на эти углы. Согласно
формуле (3.5) поворот вектора происходит
при полуширине щели равной
![]()
![]() и
т. д., когда она открывает на световом
фронте, соответственно, 3, 4, …N
и т.д., зон Шустера. Наглядно процесс
суммирования элементарных векторов в
интеграле (3.5) удобно представить как
перемещение конца вектора суммарного
светового поля
и
т. д., когда она открывает на световом
фронте, соответственно, 3, 4, …N
и т.д., зон Шустера. Наглядно процесс
суммирования элементарных векторов в
интеграле (3.5) удобно представить как
перемещение конца вектора суммарного
светового поля
![]() по некоторой кривой, изображенной на
рис.3.3, называемой спиралью
Корню .
по некоторой кривой, изображенной на
рис.3.3, называемой спиралью
Корню .
И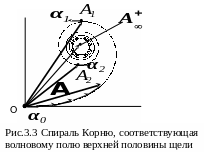 з
рис.3.3 видно, что при увеличении ширины
щели длина вектора
,
определяющая полную амплитуду светового
поля в точке наблюдения, возрастает, а
сам вектор поворачивается. Максимальная
длина вектора, определяющая наибольшую
амплитуду светового поля, достигается
вблизи точки A1
, когда открыта первая зона Шустера. С
увеличением ширины щели длина суммарного
вектора, т .е. амплитуда светового поля
в точке наблюдения, уменьшается и
достигает минимума вблизи точки A2
когда открыты две зоны Шустера. При
возрастании ширины щели суммарный
вектор осциллирует, его длина и фаза
периодически изменяются, и определяемая
вектором амплитуда светового поля в
точке наблюдения периодически возрастает
и уменьшается. Можно показать, что
площадь зоны Шустера уменьшается с
ростом номера, следовательно, ее вклад
в суммарное поле уменьшается даже в
приближении постоянной амплитуды поля
з
рис.3.3 видно, что при увеличении ширины
щели длина вектора
,
определяющая полную амплитуду светового
поля в точке наблюдения, возрастает, а
сам вектор поворачивается. Максимальная
длина вектора, определяющая наибольшую
амплитуду светового поля, достигается
вблизи точки A1
, когда открыта первая зона Шустера. С
увеличением ширины щели длина суммарного
вектора, т .е. амплитуда светового поля
в точке наблюдения, уменьшается и
достигает минимума вблизи точки A2
когда открыты две зоны Шустера. При
возрастании ширины щели суммарный
вектор осциллирует, его длина и фаза
периодически изменяются, и определяемая
вектором амплитуда светового поля в
точке наблюдения периодически возрастает
и уменьшается. Можно показать, что
площадь зоны Шустера уменьшается с
ростом номера, следовательно, ее вклад
в суммарное поле уменьшается даже в
приближении постоянной амплитуды поля
![]() в
интеграле (3.5). При большой ширине щели
вклад в суммарное поле зон с большими
номерами становится пренебрежимо малым,
и суммарный вектор поля приближается
к точке
в
интеграле (3.5). При большой ширине щели
вклад в суммарное поле зон с большими
номерами становится пренебрежимо малым,
и суммарный вектор поля приближается
к точке
![]() (полюсу),
так что его фаза, длина (
(полюсу),
так что его фаза, длина (![]() ),
и следовательно, амплитуда светового
поля в точке наблюдения, практически
перестают зависеть от ширины щели.
),
и следовательно, амплитуда светового
поля в точке наблюдения, практически
перестают зависеть от ширины щели.
Рассмотренная
картина соответствует последовательному
открыванию верхней половины щели. При
открывании нижней половины щели суммарный
вектор поля от этой части объекта также
описывает спираль Корню, расположенную
симметрично в нижней полуплоскости.
При открытых полностью обеих половинах
щели суммарный вектор поля в точке
наблюдения О1
изображается вектором
![]() ,
соединяющим полюса половинок спирали
Корню, длина которого в два раза больше
длины вектора поля от половины щели
.
Интенсивность светового поля в точке
О1
при этом возрастает в четыре раза. Полная
картина распределения интенсивности
светового поля на краю экрана, приведена
на рис.3.4.
,
соединяющим полюса половинок спирали
Корню, длина которого в два раза больше
длины вектора поля от половины щели
.
Интенсивность светового поля в точке
О1
при этом возрастает в четыре раза. Полная
картина распределения интенсивности
светового поля на краю экрана, приведена
на рис.3.4.
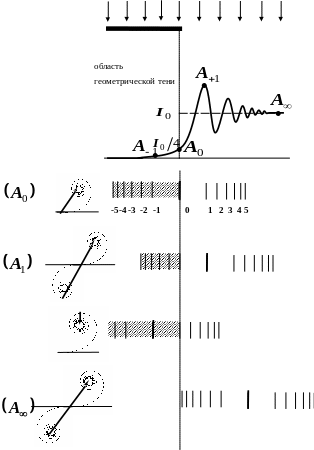
Рис.3.4.
Распределение
интенсивности светового поля при
дифракции плоского светового фронта
на краю экрана (верхний рисунок) и
построение вектора светового поля для
четырех точек распределения с помощью
спирали Корню (нижние рисунки слева).
Справа изображена структура зон Шустера
для каждой точки, закрытые экраном зоны
заштрихованы.![]()
Лекция 12.
Приближение Френеля. Дифракция Френеля.
В соответствии с
принципом Гюйгенса-Френеля суммирование
вторичных волн в произвольной точке
наблюдения
![]() производится
с помощью интеграла
Гюйгенса-Френеля,
который имеет вид:
производится
с помощью интеграла
Гюйгенса-Френеля,
который имеет вид:
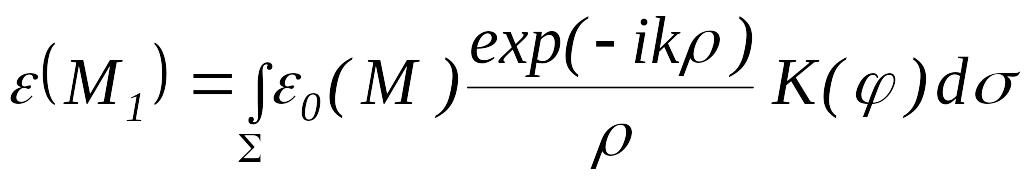 .
(3.1)
.
(3.1)
Здесь
![]() и
и
![]() 0
0![]() ,
соответственно, амплитуды суммарного
волнового поля в точке наблюдения M1
и поля элементарного вторичного источника
площадью
,
расположенного в произвольной точке
М
открываемого объектом волнового фронта
падающей волны; второй множитель в
подынтегральном выражении описывает
пространственную часть сферической
волны, излучаемой элементарным источником,
а множитель
учитывает, что вклад элемента
в суммарное поле зависит от угла
между нормалью к площади элемента и
направлением радиус - вектора
в точку наблюдения (см. рис.3.1):
,
соответственно, амплитуды суммарного
волнового поля в точке наблюдения M1
и поля элементарного вторичного источника
площадью
,
расположенного в произвольной точке
М
открываемого объектом волнового фронта
падающей волны; второй множитель в
подынтегральном выражении описывает
пространственную часть сферической
волны, излучаемой элементарным источником,
а множитель
учитывает, что вклад элемента
в суммарное поле зависит от угла
между нормалью к площади элемента и
направлением радиус - вектора
в точку наблюдения (см. рис.3.1):
. (3.1)
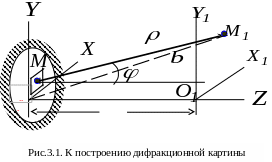 Интегрирование
в выражении (3.1) производится по всем
элементам светового фронта суммарной
площадью
Интегрирование
в выражении (3.1) производится по всем
элементам светового фронта суммарной
площадью![]() ,
открываемым объектом. Запишем формулу
(3.1) в координатном представлении
предполагая, что углы
дифракции малы
,
открываемым объектом. Запишем формулу
(3.1) в координатном представлении
предполагая, что углы
дифракции малы
![]() ,
т.е.
,
т.е.
![]() ,
и, следовательно, амплитуда поля в
интеграле (3.1) не зависит от положения
элемента светового фронта:
,
и, следовательно, амплитуда поля в
интеграле (3.1) не зависит от положения
элемента светового фронта:
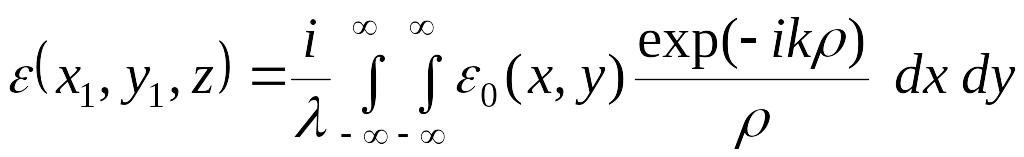 ,
(3.2
)
,
(3.2
)
где
![]() .
.
Упростим формулу (3.2), полагая, что в приближении Френеля дифракционное уширение изображения мало вследствие малости углов дифракции:
![]() .
.
Для этого случая
в быстро осциллирующем на длине волны
показателе экспоненты представим
радиус-вектор ρ
в приближенном
виде, сохранив члены, квадратичные
по углам дифракции
![]() :
:
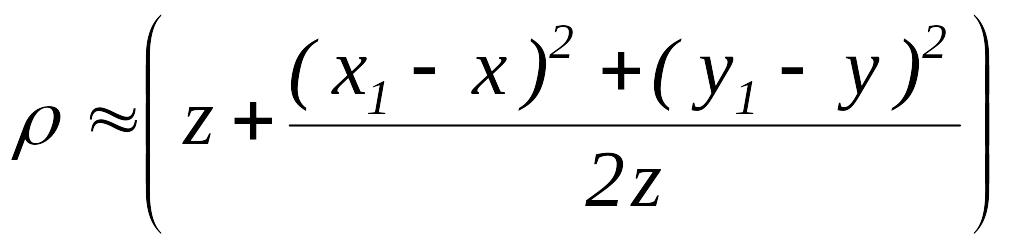 ,
(3.3)
,
(3.3)
а в медленно
меняющемся при перемещении по области
интегрирования знаменателе подынтегрального
выражения полагаем
![]() .
С помощью полученного интеграла
Френеля
.
С помощью полученного интеграла
Френеля
![]()
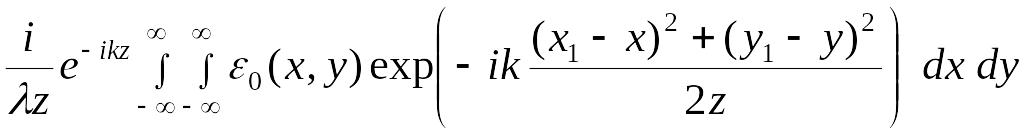 (3.4)
(3.4)
можно построить картину дифракции светового фронта на простых объектах: отверстии, щели, краю экрана. При этом показатель экспоненты под интегралом может принимать любые по модулю значения, как больше, так и меньше единицы.
Приближение Фраунгофера.
![]() << 1. В этом
случае, называемом дифракцией
Фраунгофера,
объект открывает небольшую часть первой
зоны Френеля, т.е. согласно формуле
(3.6), дифракционная картина рассматривается
на больших расстояниях от объекта (в
дальней
зоне).
Поэтому, в отличие от предыдущих случаев,
размер изображения даже при малых углах
дифракции существенно превосходит
размер объекта (см. рис.3.6в), т.е. здесь
потеряна информация уже и о размере
объекта. Разложение радиус-вектора
<< 1. В этом
случае, называемом дифракцией
Фраунгофера,
объект открывает небольшую часть первой
зоны Френеля, т.е. согласно формуле
(3.6), дифракционная картина рассматривается
на больших расстояниях от объекта (в
дальней
зоне).
Поэтому, в отличие от предыдущих случаев,
размер изображения даже при малых углах
дифракции существенно превосходит
размер объекта (см. рис.3.6в), т.е. здесь
потеряна информация уже и о размере
объекта. Разложение радиус-вектора
![]() теперь проведем следующим образом:
теперь проведем следующим образом:
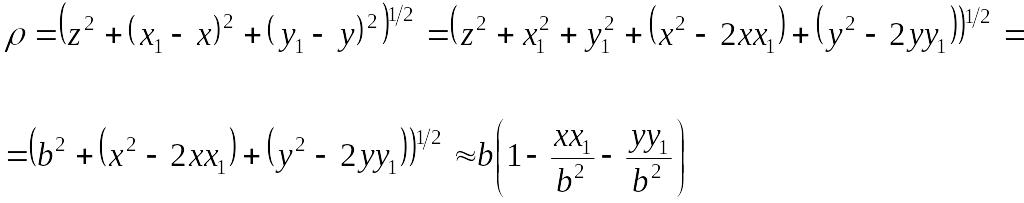
В этом разложении,
мы пренебрегли малым членом разложения
пропорциональным
![]() ,
т.е. теперь, в отличие от приближения
Френеля, ограничились только линейными
членами в
разложении
,
т.е. теперь, в отличие от приближения
Френеля, ограничились только линейными
членами в
разложении
![]() по малому параметру - отношению размера
объекта к расстоянию до него. Интеграл
(3.4) тогда имеет вид
по малому параметру - отношению размера
объекта к расстоянию до него. Интеграл
(3.4) тогда имеет вид
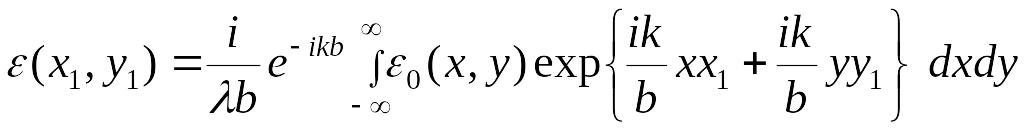 .
(3.7)
.
(3.7)
Дифракция Фраунгофера как пространственное преобразование Фурье функции пропускания объекта
Из формулы (3.7)
видно, что в используемом приближении
дифракционная картина зависит лишь от
угловой координаты точки наблюдения
![]() и
и
![]() ,
с другой
стороны проекции вектора
,
с другой
стороны проекции вектора
![]() ,
,
![]() .
.
Рассмотрим выражение
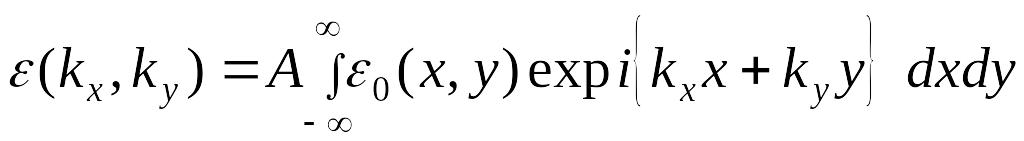 .
(3.8)
.
(3.8)
Интеграл (3.8) с
математической точки зрения представляет
собой пространственное преобразование
Фурье амплитуды поля исходного пучка
![]() по поперечным
компонентам волнового вектора
по поперечным
компонентам волнового вектора
![]() ,
направленного из точки O
в точку наблюдения поля M1.
Здесь введено обозначение
,
направленного из точки O
в точку наблюдения поля M1.
Здесь введено обозначение
![]() .
Выражение (3.8) показывает, что дифракция
Фраунгофера на каком-либо объекте имеет
смысл пространственного
разложения на плоские волны
светового пучка, ограниченного этим
объектом. Полученная дифракционная
картина представляет собой Фурье-образ
(спектр пространственных частот) поля
волны, прошедшей через объект.
.
Выражение (3.8) показывает, что дифракция
Фраунгофера на каком-либо объекте имеет
смысл пространственного
разложения на плоские волны
светового пучка, ограниченного этим
объектом. Полученная дифракционная
картина представляет собой Фурье-образ
(спектр пространственных частот) поля
волны, прошедшей через объект.
Удобной характеристикой
объекта является функция пропускания
![]() ,
которая задается его поперечной
структурой и определяется как отношение
комплексной амплитуды прошедшей волны,
которую будем теперь обозначать как
,
которая задается его поперечной
структурой и определяется как отношение
комплексной амплитуды прошедшей волны,
которую будем теперь обозначать как
![]() ,
к амплитуде падающей волны
,
к амплитуде падающей волны
![]()
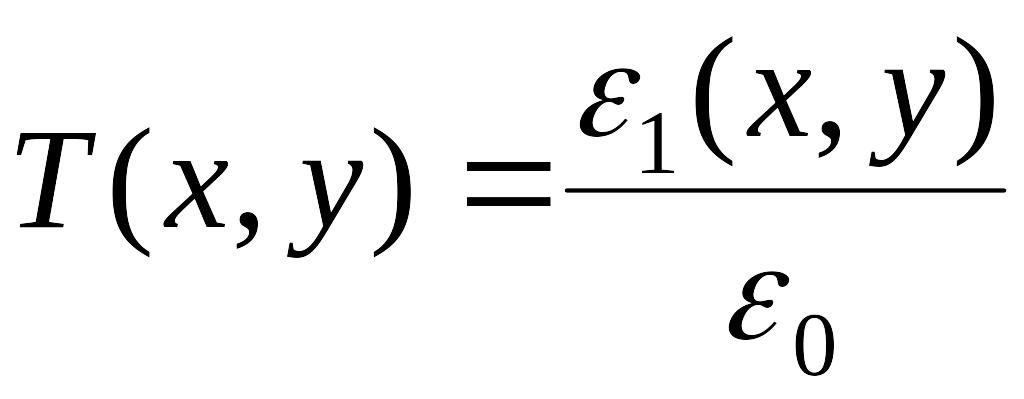 .
.
Двумерный интеграл вида (3.8) в случае однородного падающего потока можно тогда рассматривать и как Фурье-преобразование функции пропускания объекта. Рассмотрим примеры построения Фурье-спектра функции пропускания для простейших объектов.
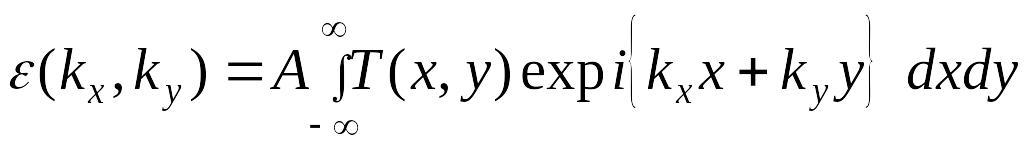
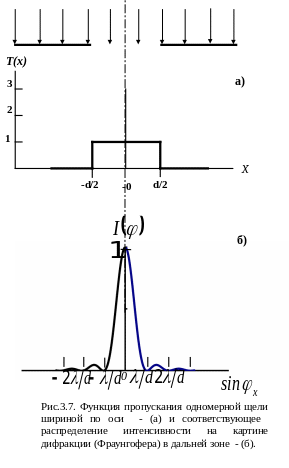
Прямоугольная щель. Функция пропускания щели имеет вид:
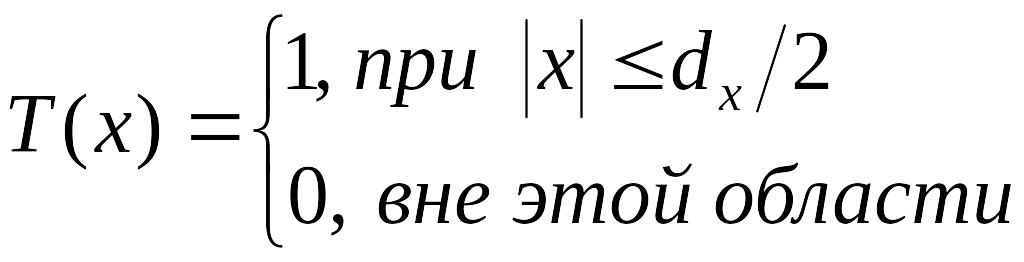 .
.
Распределение
амплитуды светового поля в плоскости
щели
![]() с точностью до константы совпадает с
этим выражением. Подставив его в интеграл
типа (3.8) по двум координатам и выполнив
интегрирование с учетом соотношения
(3.7) находим амплитуду светового поля в
дальней зоне:
с точностью до константы совпадает с
этим выражением. Подставив его в интеграл
типа (3.8) по двум координатам и выполнив
интегрирование с учетом соотношения
(3.7) находим амплитуду светового поля в
дальней зоне:
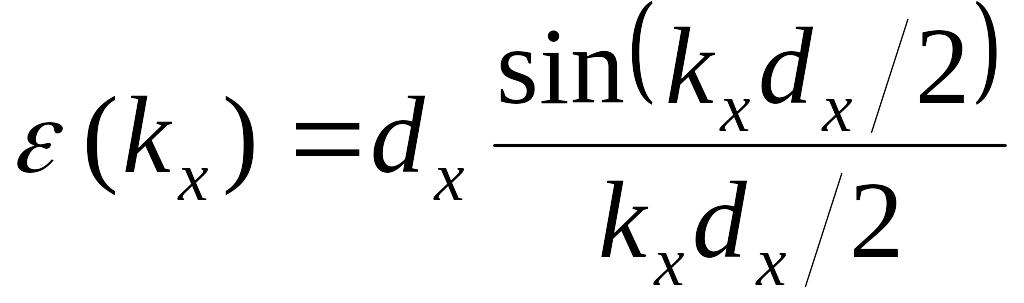
или
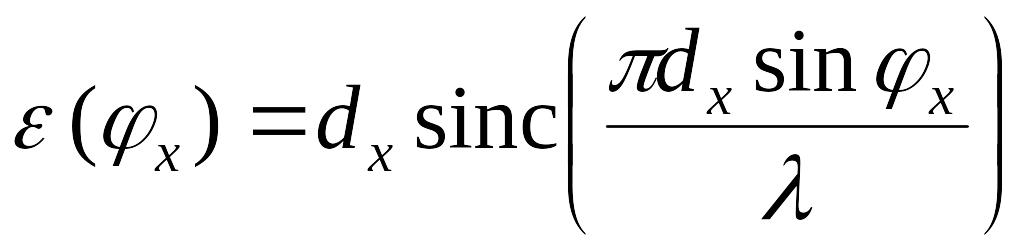 ,
(3.10)
,
(3.10)
где введено
обозначение
![]() .
Распределение интенсивности светового
поля пропорционально квадрату этого
выражения, а его сечение вдоль оси
.
Распределение интенсивности светового
поля пропорционально квадрату этого
выражения, а его сечение вдоль оси
![]() изображено на рис. 3.7.
изображено на рис. 3.7.
Из формул (3.9)
найдем угловую ширину главного (нулевого)
максимума дифракционной картины по
одной из осей
![]() ,
а ширину по оси
,
а ширину по оси
![]() определим
из условия
определим
из условия
![]() .
Поскольку амплитуда первого максимума
интенсивности составляет около 4%
амплитуды нулевого, почти весь световой
поток сосредоточен в пределах именно
нулевого максимума, и полученные формулы
определяют фактически ширину спектра
по углу
.
Поскольку амплитуда первого максимума
интенсивности составляет около 4%
амплитуды нулевого, почти весь световой
поток сосредоточен в пределах именно
нулевого максимума, и полученные формулы
определяют фактически ширину спектра
по углу
![]() или оси
или оси
![]()
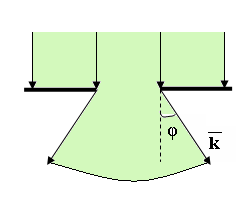
Рассмотрим
физический смысл этого выражения с
другой точки зрения. Для этого рассмотрим
световой поток как поток квантов света
(фотонов). Умножив на
![]() обе части этого равенства, получим
обе части этого равенства, получим
![]()
![]() ,
,
где
![]() -ширина
спектра импульсов потока фотонов,
прошедших щель шириной
-ширина
спектра импульсов потока фотонов,
прошедших щель шириной
![]() .
Полученное равенство можно рассматривать
как сохранение при произвольном изменении
ширины щели, произведения размера потока
фотонов в координатном пространстве
на его “размер” в импульсном пространстве,
т.е. фазового объема потока. Этот вывод
является иллюстрацией фундаментального
физического принципа
неопределенности,
справедливого не только для квантов
электромагнитного поля, но и для любых
других
.
Полученное равенство можно рассматривать
как сохранение при произвольном изменении
ширины щели, произведения размера потока
фотонов в координатном пространстве
на его “размер” в импульсном пространстве,
т.е. фазового объема потока. Этот вывод
является иллюстрацией фундаментального
физического принципа
неопределенности,
справедливого не только для квантов
электромагнитного поля, но и для любых
других
объектов, обладающих волновыми свойствами (например, электронов, протонов и др.).
Круглое отверстие. Функция пропускания для отверстия радиуса
 имеет вид:
имеет вид:
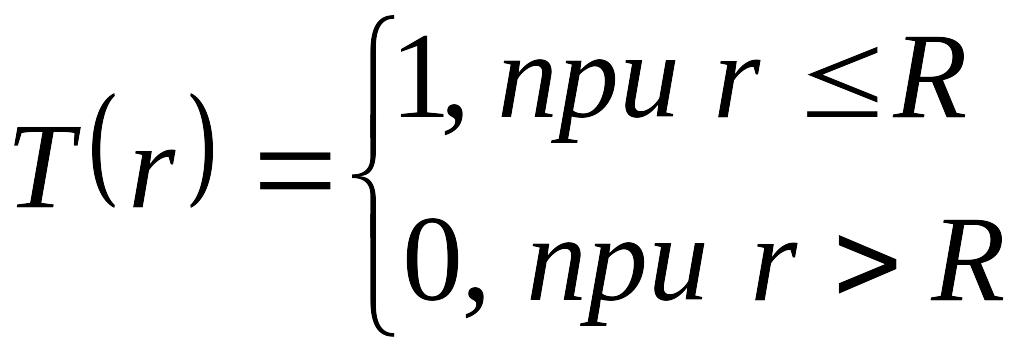 .
.
Действуя
так же, как в предыдущем пункте, придем
к двумерному интегралу вида (3.8) в полярных
координатах
![]() ,
который после интегрирования по углу
принимает вид:
,
который после интегрирования по углу
принимает вид:
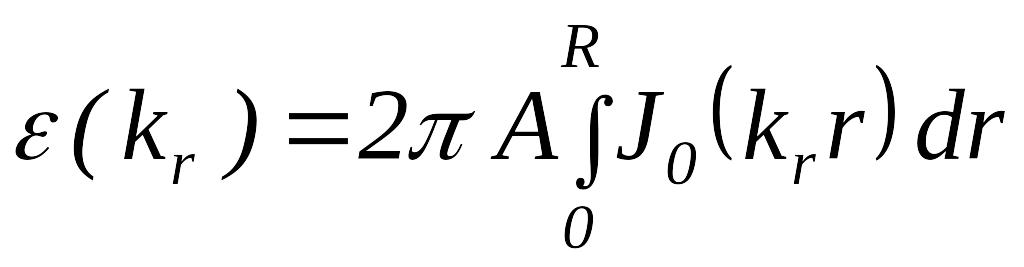 ,
(3.9)'
,
(3.9)'
где
![]() -
специальная функция (Бесселя) нулевого
порядка. Этот интеграл выражается через
функцию Бесселя первого порядка.
Качественно полученная дифракционная
картина аналогична описанной выше, и
представляет собой центральное яркое
пятно круглой формы, окруженное системой
концентрических темных и светлых колец,
соответствующих последовательным
минимумам и максимумам интенсивности.
Угловой размер центрального максимума
(пятна Эйри), где сосредоточен, как и в
предыдущем случае, практически весь
световой поток, равен
-
специальная функция (Бесселя) нулевого
порядка. Этот интеграл выражается через
функцию Бесселя первого порядка.
Качественно полученная дифракционная
картина аналогична описанной выше, и
представляет собой центральное яркое
пятно круглой формы, окруженное системой
концентрических темных и светлых колец,
соответствующих последовательным
минимумам и максимумам интенсивности.
Угловой размер центрального максимума
(пятна Эйри), где сосредоточен, как и в
предыдущем случае, практически весь
световой поток, равен
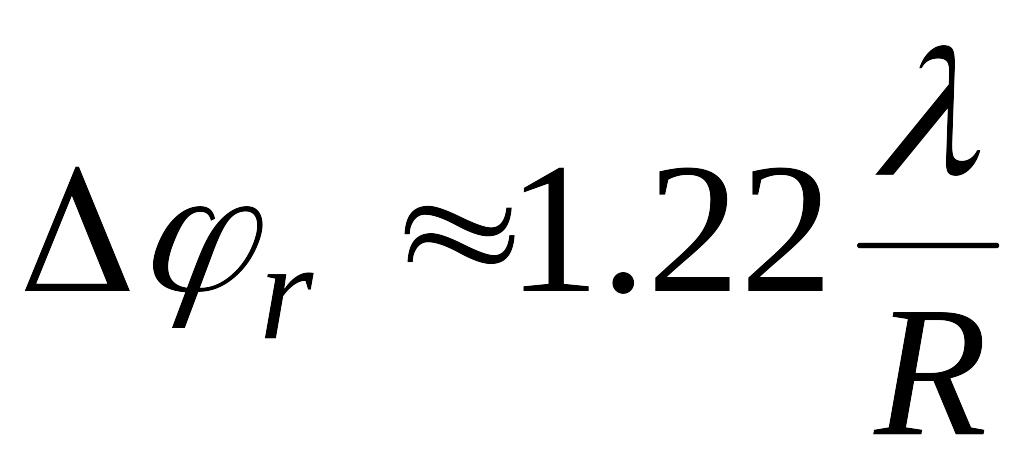 .
(3.9)"
.
(3.9)"
3) Дифракционная решетка. Для случая прямоугольной (одномерной) амплитудной решетки функция пропускания имеет вид (см. рис.3.8):
![]()
![]() ,
,
где N
– число штрихов,
![]() =
=
![]() -
координата левой границы n-го
штриха,
-
координата левой границы n-го
штриха,
![]() -
функция пропускания
-
функция пропускания
![]() -го
штриха:
-го
штриха:
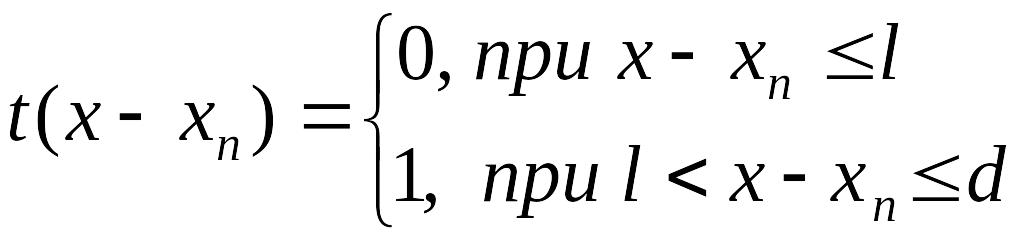 .
.
Из рис. 3.8 видно,
что функция пропускания решетки
характеризуется тремя пространственными
масштабами: шириной штриха
![]() ,
периодом
и полным размером
,
периодом
и полным размером
![]()
![]() .
При интегрировании функции пропускания
-ого
штриха можно заметить, что фаза плоской
волны
.
При интегрировании функции пропускания
-ого
штриха можно заметить, что фаза плоской
волны
![]() состоит
из двух слагаемых: первое меняется
непрерывно на ширине штриха, второе –
дискретно, с шагом
,
при переходе от одного штриха к другому.
состоит
из двух слагаемых: первое меняется
непрерывно на ширине штриха, второе –
дискретно, с шагом
,
при переходе от одного штриха к другому.
В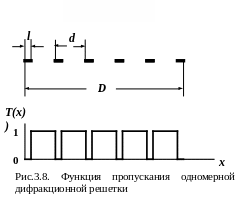 соответствии с этим, распределение
амплитуды светового поля дифракционной
картины в дальней зоне имеет вид
произведения двух функций:
соответствии с этим, распределение
амплитуды светового поля дифракционной
картины в дальней зоне имеет вид
произведения двух функций:
![]() ,
,
где первый множитель описывает дифракцию на отдельном штрихе и аналогичен выражению, полученному в предыдущем пункте:
![]() .
.
Второй множитель возникает вследствие суммирования (интерференции) волн, испускаемых штрихами как точечными источниками с координатами , и вычисляется как сумма членов геометрической прогрессии:
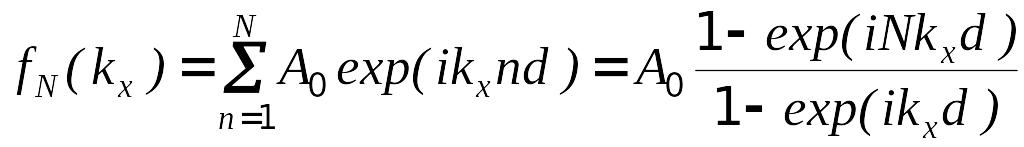 .
.
Учитывая,
что
![]() и переходя к интенсивностям светового
поля согласно формуле:
и переходя к интенсивностям светового
поля согласно формуле:
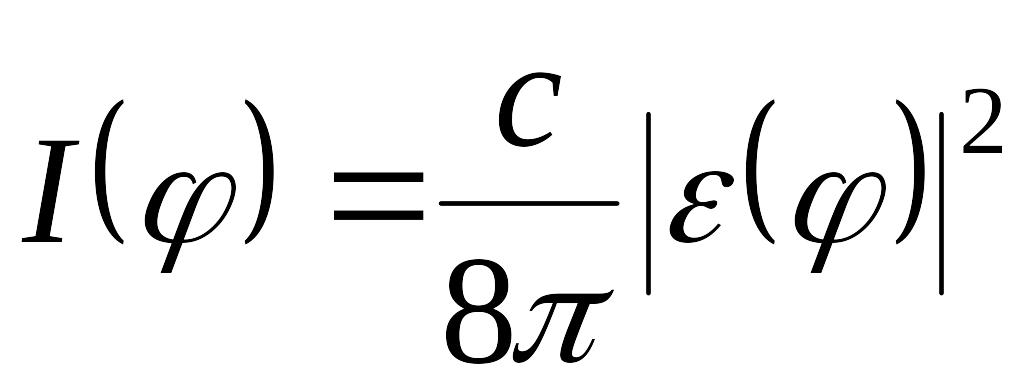 ,
,
получим
![]() .
(3.10)
.
(3.10)
Здесь введены обозначения:
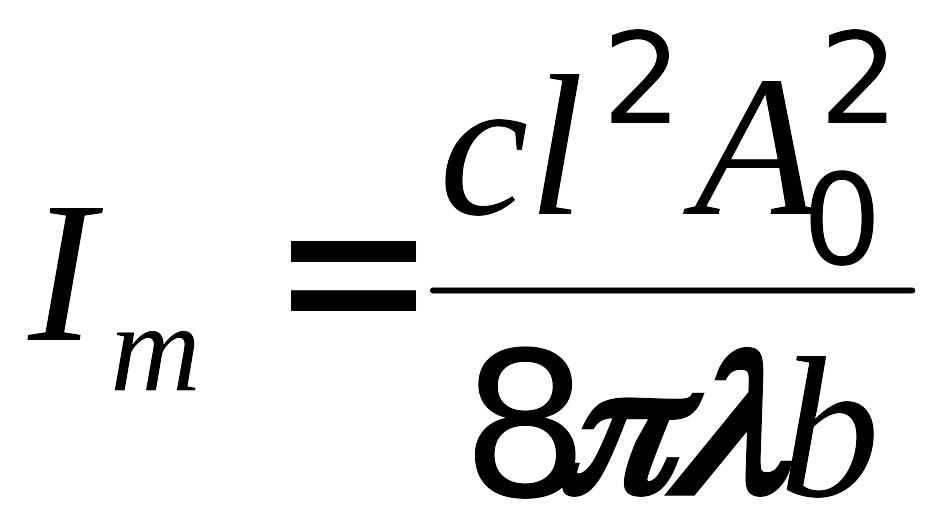 ,
,
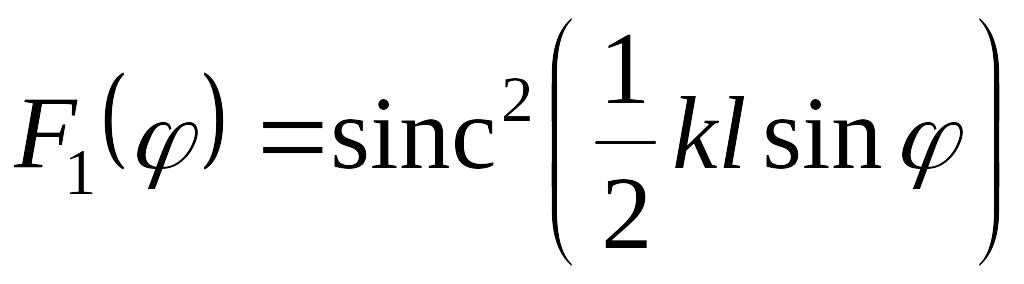 ,
(3.11)
,
(3.11)
 (3.12)
(3.12)
Вид
функций
![]() показан на рис.(3.9). Из рисунка следует,
что в структуре дифракционной картины
наблюдаются три характерных угловых
масштаба:
показан на рис.(3.9). Из рисунка следует,
что в структуре дифракционной картины
наблюдаются три характерных угловых
масштаба:
Расстояние между соседними главными максимумами
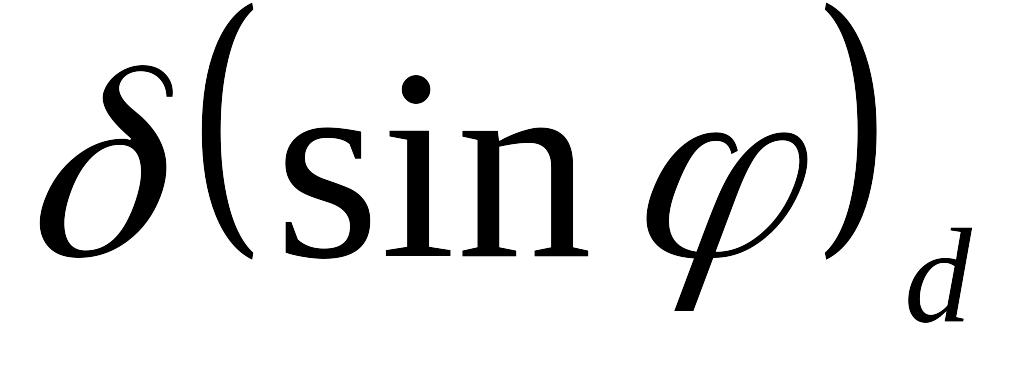 ,
Оно находится из условия, что
распространяющиеся в направлении
главных максимумов
,
Оно находится из условия, что
распространяющиеся в направлении
главных максимумов
 волны, которые излучаются точками
решетки, разнесенными на период
,
усиливают друг друга, т.е. их разность
фаз кратна
волны, которые излучаются точками
решетки, разнесенными на период
,
усиливают друг друга, т.е. их разность
фаз кратна
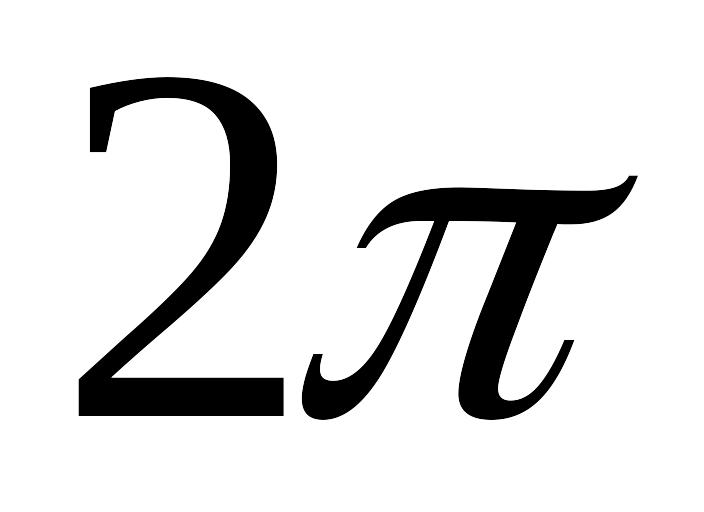 :
:
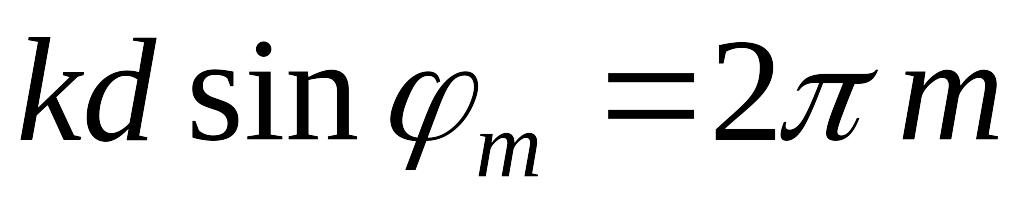 ,
или
,
или
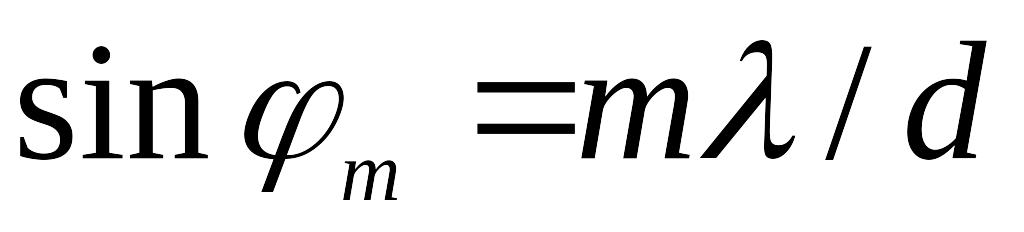 и
и
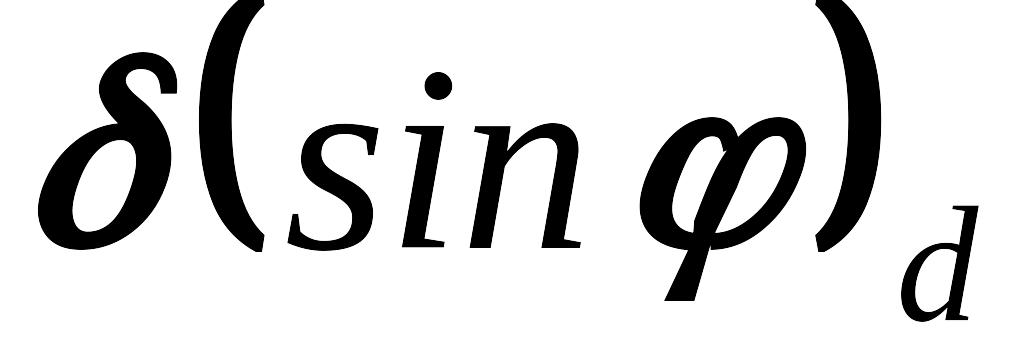
 .
Здесь
.
Здесь

![]() ,
а максимальный порядок дифракции
,
а максимальный порядок дифракции
![]() определяется
неравенством
определяется
неравенством
![]() .
Из формулы (3.12) видно, что для этих
направлений
.
Из формулы (3.12) видно, что для этих
направлений
![]() ,
т.е. интенсивность суммарного светового
поля в главных максимумах действительно
возрастает в
раз
по сравнению с полем одного штриха.
,
т.е. интенсивность суммарного светового
поля в главных максимумах действительно
возрастает в
раз
по сравнению с полем одного штриха.
Ширина главных максимумов
 ,
которая для
-ого
максимума находится из условия, что
под углом
,
которая для
-ого
максимума находится из условия, что
под углом
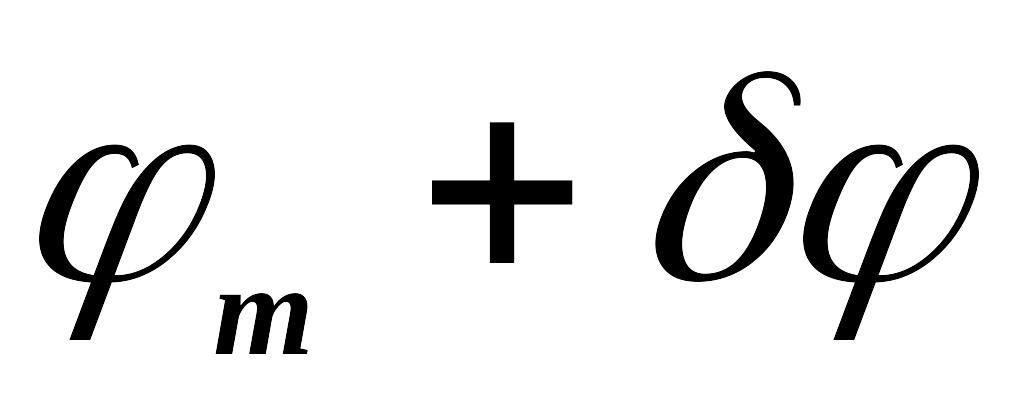 наблюдается ближайший минимум, т.е.,
согласно формуле (3.12):
наблюдается ближайший минимум, т.е.,
согласно формуле (3.12):
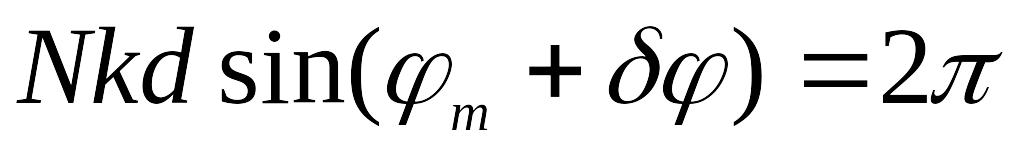 ,
или
,
или
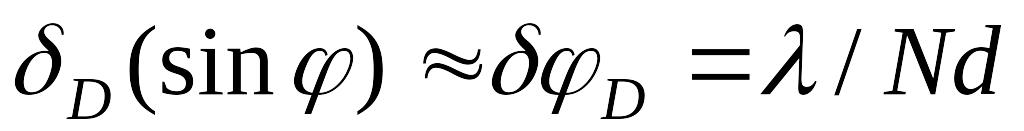 =
=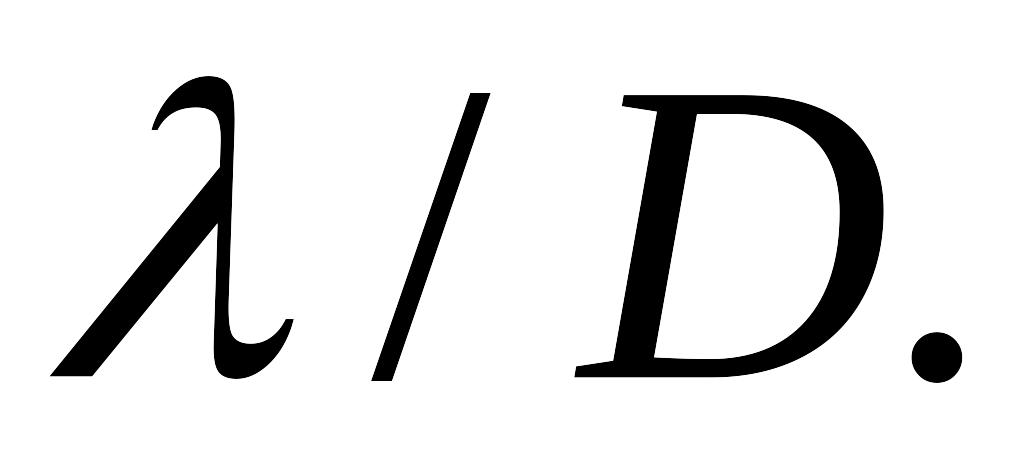
Ширина всей картины
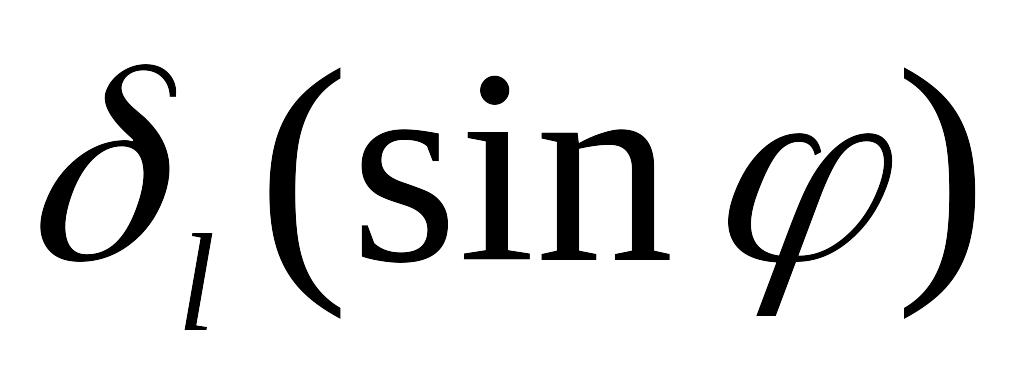 ,
определяемая характерной шириной
функции
,
определяемая характерной шириной
функции
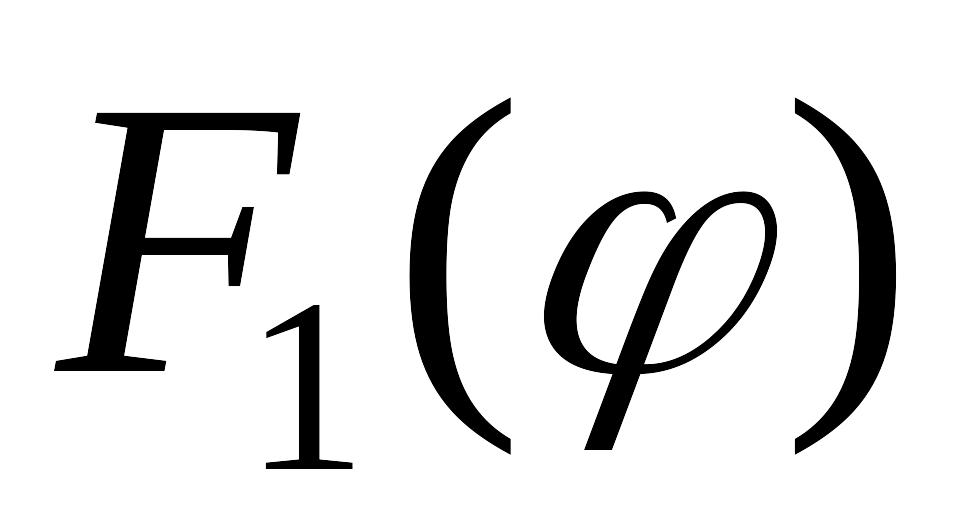 ,
т.е. условием
,
т.е. условием
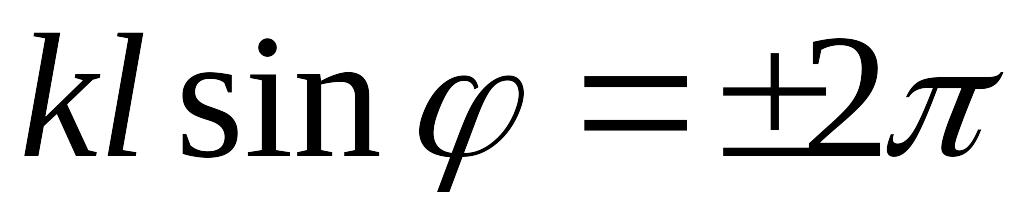 .
Отсюда
.
Отсюда
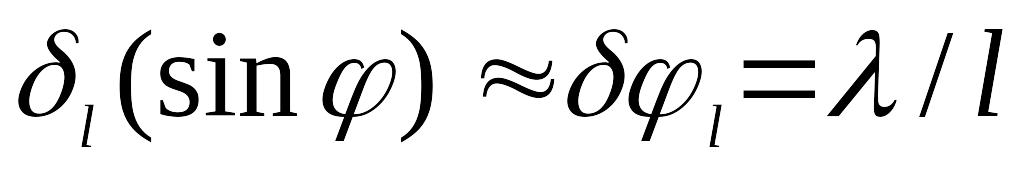 .
.
Этим
трем масштабам (![]() )
в дифракционной картине, представляющей
собой Фурье – спектр функции пропускания
по переменной
)
в дифракционной картине, представляющей
собой Фурье – спектр функции пропускания
по переменной
![]() ,
соответствуют три пространственных
масштаба в самой функции
,
соответствуют три пространственных
масштаба в самой функции
![]() :
:
![]() ,
причем, как видно из формул для
,
причем, как видно из формул для
![]() ,
в соответствии с общими свойствами
Фурье-преобразования, каждый масштаб
в объекте обратно пропорционален
соответствующему масштабу в его спектре.
,
в соответствии с общими свойствами
Фурье-преобразования, каждый масштаб
в объекте обратно пропорционален
соответствующему масштабу в его спектре.
Из
рис. 3.9 также видно, что картина дифракции
на периодической структуре содержит в
интерференционном члене
![]() информацию о параметрах этой структуры.
В частности, период
структуры
можно найти из углового расстояния
между соседними главными максимумами:
информацию о параметрах этой структуры.
В частности, период
структуры
можно найти из углового расстояния
между соседними главными максимумами:
![]() .
Количество
элементов
структуры
связано с числом минимумов между
соседними главными максимумами.
Действительно, направления на минимумы
.
Количество
элементов
структуры
связано с числом минимумов между
соседними главными максимумами.
Действительно, направления на минимумы
![]() находятся из условия обращения в нуль
числителя при ненулевом знаменателе,
т.е.
находятся из условия обращения в нуль
числителя при ненулевом знаменателе,
т.е.
![]() ,
но при этом необходимо обеспечить
условие, чтобы
,
но при этом необходимо обеспечить
условие, чтобы
![]()
![]() .
Отсюда получим
.
Отсюда получим
![]() .
Для случая, когда
.
Для случая, когда
![]() ,
в дифракционной картине остается
единственный (нулевой) главный максимум,
и она теряет информацию о структуре
объекта. Этот случай соответствует
переходу от дифракции на объекте с
периодической структурой (т.е., фактически,
многолучевой интерференции) к дифракции
на объекте, как целом.
,
в дифракционной картине остается
единственный (нулевой) главный максимум,
и она теряет информацию о структуре
объекта. Этот случай соответствует
переходу от дифракции на объекте с
периодической структурой (т.е., фактически,
многолучевой интерференции) к дифракции
на объекте, как целом.
Рассмотрим
этот переход подробнее. Определим
нормировочный множитель, полагая
амплитуду поля, падающего на всю решетку,
равной единице, тогда
![]() .
Зафиксируем размер дифракционной
решетки
.
Зафиксируем размер дифракционной
решетки![]() ,
и будем увеличивать число штрихов
,
т.е. уменьшать период
.
Тогда при достаточно большом
выполняется
неравенство
,
и будем увеличивать число штрихов
,
т.е. уменьшать период
.
Тогда при достаточно большом
выполняется
неравенство
![]() ,
и интерференционный множитель
,
и интерференционный множитель
![]() преобразуется к виду:
преобразуется к виду:
 (3.12’).
(3.12’).
Это выражение аналогично формуле (3.11) и описывает картину дифракции на «штрихе» шириной .
Дифракция на апертурах.(Фраунгофера.)
Получили
![]()
![]()
Данные выражения определяют угловое распределение в дифракционной картине.
Аналогия:
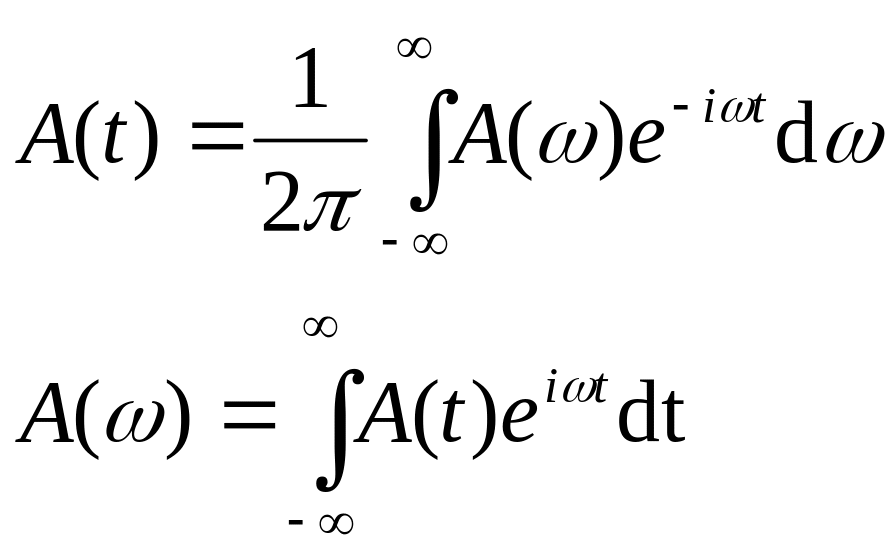
В случае дифракции вводятся пространственные частоты
![]()
![]() ,
где
,
где
![]()
![]() .
.
Если
![]() ,
где
,
где
![]() ,
а
,
а
![]() -
сдвиг фаз, набираемый на апертуре, то
можно описать дифракцию на любом объекте.
Фактически мы ввели фазовый коэффициент
пропускания. Если на апертуру падает
волна
-
сдвиг фаз, набираемый на апертуре, то
можно описать дифракцию на любом объекте.
Фактически мы ввели фазовый коэффициент
пропускания. Если на апертуру падает
волна
![]() ,
после нее
,
после нее
![]() .
.
