
- •§1.1. Уравнения Максвелла.
- •§1.2 Электромагнитные волны в вакууме.
- •Волновое уравнение в вакууме.
- •Комплесксная форма записи.
- •Сферические волны .
- •1.2.6. Энергетические характеристики.
- •2.2 Физика теплового излучение
- •2.2.1 Формула Планка.
- •3.Квантовые представления
- •4.Анализ
- •Физика оптического излучения. Основы физики лазеров.
- •2. Вынужденное (индуцированное) поглощение.
- •3. Вынужденное излучение.
- •Интерференция света Общий закон интерференции
- •Интерференция от двух точечных монохроматических источников
- •Когерентность.
- •II. Пространственная когерентность.
- •Дифракция на прямоугольной апертуре.
- •Дифракция на круглом отверстии.
- •Разрешающая способность телескопа
- •Дифракция Гауссова пучка.
- •4.1. Распространение света в изотропных средах.
- •4.1.3 .Оптические свойства сред в ик, видимой и уф областях спектра.
- •4.2 Распространение немонохроматических волн в изотропных средах.
- •Временное преобразование . Сжатие импульса.
- •4.2 Оптика анизотропных сред.
- •4.2.6. Двойное лучепреломление, построения Гюйгенса для анизотропных сред.
- •4.5 Нелинейная оптика. Оптика сильных световых полей.
- •4.5.1 Исторический обзор.
- •4.5.2 Ангармонический осциллятор. Нелинейная поляризация.
- •Генерация второй гармоники – волновая картина. Условие пространственного синхронизма
- •Получение генерации суммарных и разностных частот
- •Зависимость показателей преломления от интенсивности света
- •Самофокусировка и самодефокусировка света
4.2 Оптика анизотропных сред.
4.2.1. Модель анизотропной среды.
М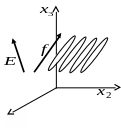 оделью
анизотропной среды является система,
состоящая из вытянутых молекул или
других комплексов, в которых оптические
электроны могут смещаться только вдоль
одного, выбранного направления. Пусть
это смещение характеризуется единичным
вектором
оделью
анизотропной среды является система,
состоящая из вытянутых молекул или
других комплексов, в которых оптические
электроны могут смещаться только вдоль
одного, выбранного направления. Пусть
это смещение характеризуется единичным
вектором
![]() .
Выбрали систему координат, в которой
произвели замену
.
Выбрали систему координат, в которой
произвели замену
![]() .
Единичный вектор
в этом случае представлен, как
.
Единичный вектор
в этом случае представлен, как
![]() .
Электроны совершают колебания под
воздействием электромагнитной волны,
напряженность электрического поля
.
Электроны совершают колебания под
воздействием электромагнитной волны,
напряженность электрического поля
![]() которой показана на рисунке.
которой показана на рисунке.
Уравнение движения оптического электрона в этом случае имеет вид:
![]() .
.
поляризация
![]() или
или
![]()
В отличии от
изотропной среды, направление поляризации
не совпадает с направлением вектора
,
то есть
![]() не
параллельно
.
не
параллельно
.
Введем диэлектрическую восприимчивость среды:
![]()
Рассмотрим скалярное произведение
![]()
![]()
![]() ,
,
тогда
![]() (1)
(1)
или
![]()
![]()
![]() .
.
Введем
тензорную диэлектрическую восприимчивость
![]() .
.
Уравнение для поляризации можно представить в виде
![]()
или
![]()
![]()
![]()
Тензор
![]() можно
записать в виде матрицы
можно
записать в виде матрицы
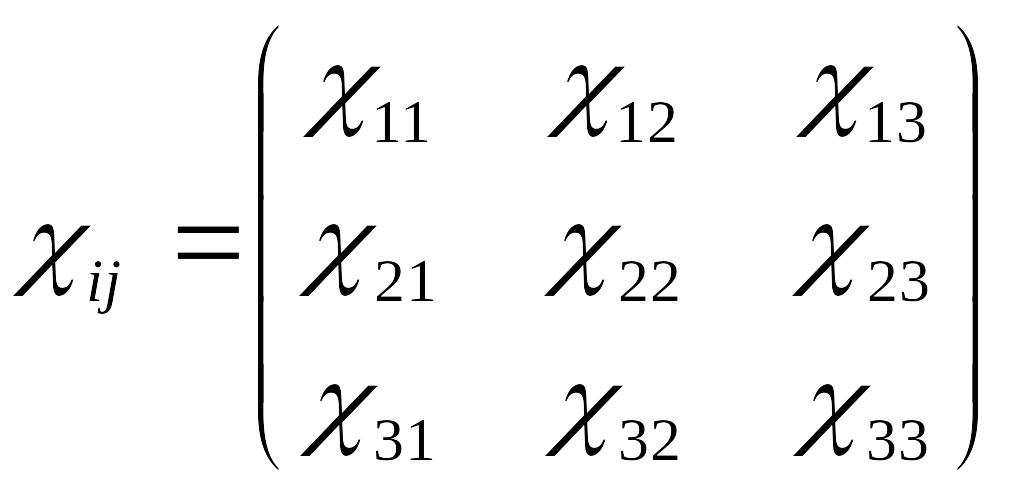
Найдем
материальное уравнение для анизотропных
сред
![]() ,
для соответствующих компонент уравнение
примет вид:
,
для соответствующих компонент уравнение
примет вид:
![]() .
.
Запишем
![]() ,
где
,
где
![]() ,
,
тогда
![]() .
.
Материальное уравнение для анизотропной среды примет вид:
![]() ,
где диэлектрическая проницаемость
,
где диэлектрическая проницаемость
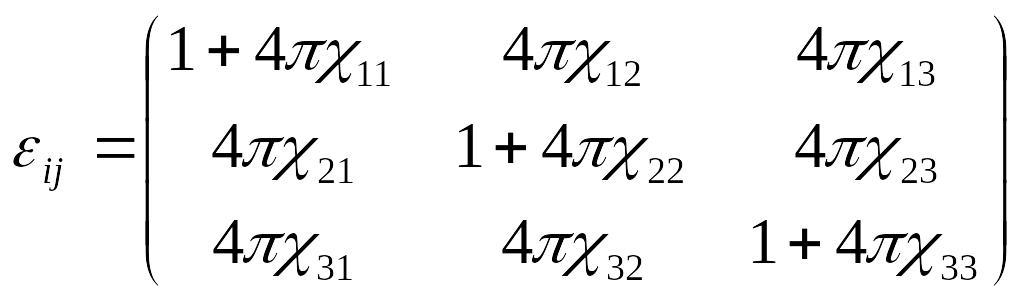
В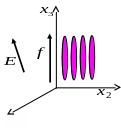 ыберем
систему координат, учитывающую симметрию
кристалла, направим ось
ыберем
систему координат, учитывающую симметрию
кристалла, направим ось![]() вдоль
вектора
,
в этой системе
вдоль
вектора
,
в этой системе
![]() ,
тогда
,
тогда
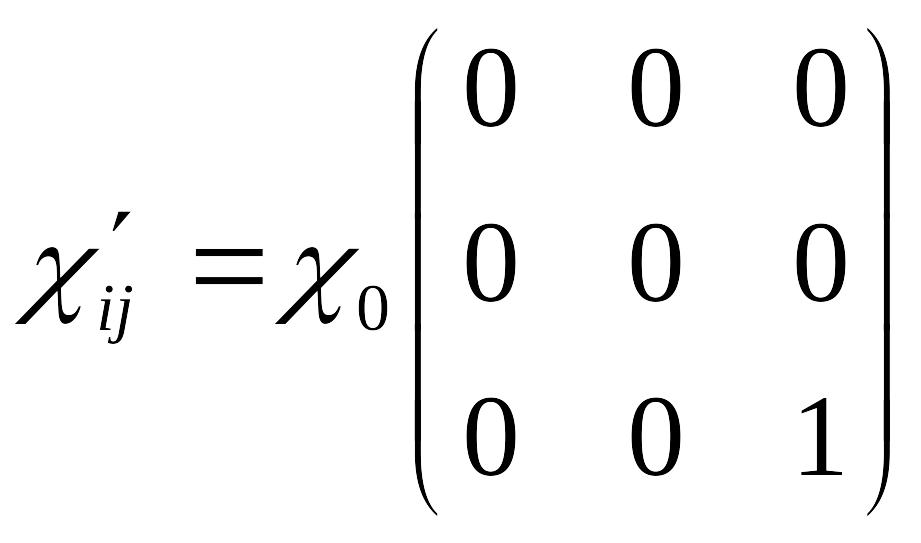 ,
,
 .
.
Матрица
![]() .
.
Всегда
можно выбрать оси координат, в которых
![]() приобретает диагональный вид
приобретает диагональный вид
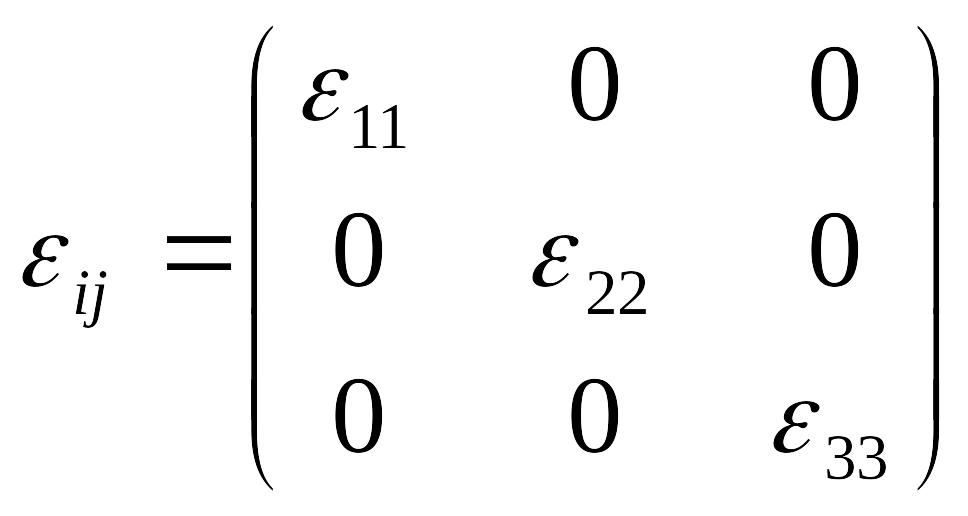
Для
этого необходимо найти собственные
значения
![]() ;
и решить уравнение
;
и решить уравнение
![]() ,
где
,
где
![]() -
собственные вектора.,
-
собственные значения.
-
собственные вектора.,
-
собственные значения.
В этой системе координат
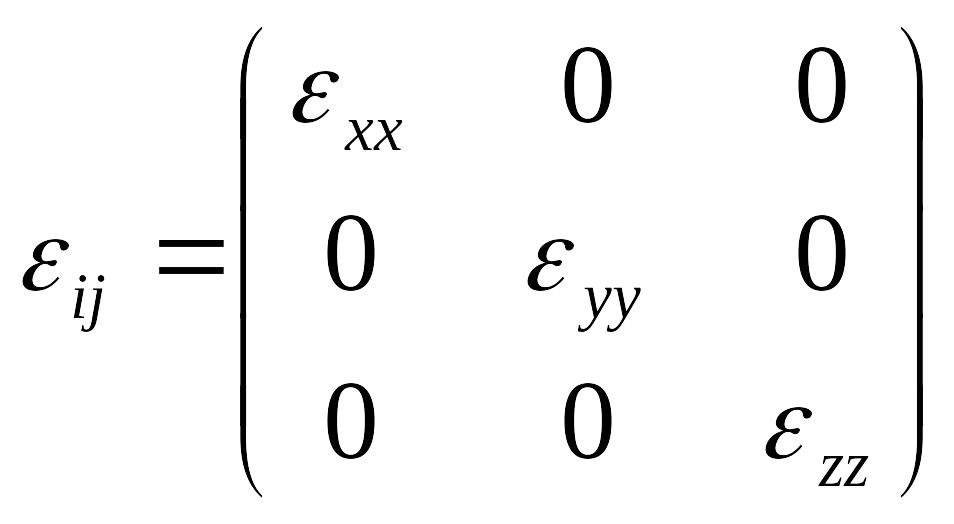
Такая система называется главной кристаллической системой координат тензора диэлектрической проницаемости .
В
этой системе связь между
![]() .
.
и
![]() следующая
следующая
![]()
![]()
![]()
Рассмотрим, когда вектор направлен вдоль одной из осей.
1
![]() в этом случае
в этом случае
![]() ,то
есть
║
,то
есть
║
Введем
главное значение показателя преломления
![]()
![]()
![]()
![]()
![]()
![]() ,
где
,
где
![]()
Если
все главные компоненты тензора
![]() ,
,![]() ,
,![]() различны по значению, то больше нет
направлений, в которых векторы
и
были бы коллинеарны.
различны по значению, то больше нет
направлений, в которых векторы
и
были бы коллинеарны.
Распространение электромагнитных волн в анизотропных средах.
Рассмотрим волну, распространяющуюся в анизотропной среде. Направление волнового вектора в такой среде характеризуется единичным вектором:
![]() .
.
Рассмотрим уравнения Максвелла:
![]()
![]() .
.
Пусть в направлении
![]() распространяется плоская электромагнитная
волна
распространяется плоская электромагнитная
волна
![]() ,
волновой вектор которой
,
волновой вектор которой
![]() .
.
Тогда можем записать:
![]()
![]()
Подставим данные выражения в уравнения Максвелла, получим
![]()
![]() ,
(*)
,
(*)
где
.
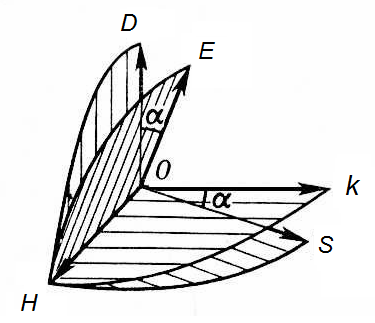
Р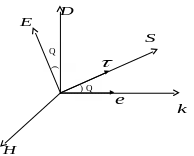 ассмотрим
ориентацию векторов
ассмотрим
ориентацию векторов
![]() ,
,
![]() ,
,
![]() ,
вектор
лежит в плоскости
,
вектор
лежит в плоскости
![]() ,
угол между
,
угол между
![]() и
называется углом анизотропии. Q5о
для кальцита.
и
называется углом анизотропии. Q5о
для кальцита.
Направление луча определяется направлением переноса энергии. Рассмотрим вектор Умова-Пойтинга.
![]() ,
при этом
,
при этом
![]() и
и
![]() ,
луч распространяется в направлении
вектора
,
луч распространяется в направлении
вектора
![]() ,
определяемом единичным вектором
,
определяемом единичным вектором
![]() .
Направления распространения фазы и
энергии не совпадают. Фаза движется по
со скоростью
.
Направления распространения фазы и
энергии не совпадают. Фаза движется по
со скоростью
![]() ,
а энергия по
со скоростью
,
а энергия по
со скоростью
![]() ,
эта скорость называется лучевой. Скорости
связаны соотношением:
,
эта скорость называется лучевой. Скорости
связаны соотношением:
![]() .
.
Уравнение нормали Френеля.
Из уравнений (*) получим
![]() .
.
![]()
Рассмотрим компоненты вектора в главной кристаллической системе

Получим:
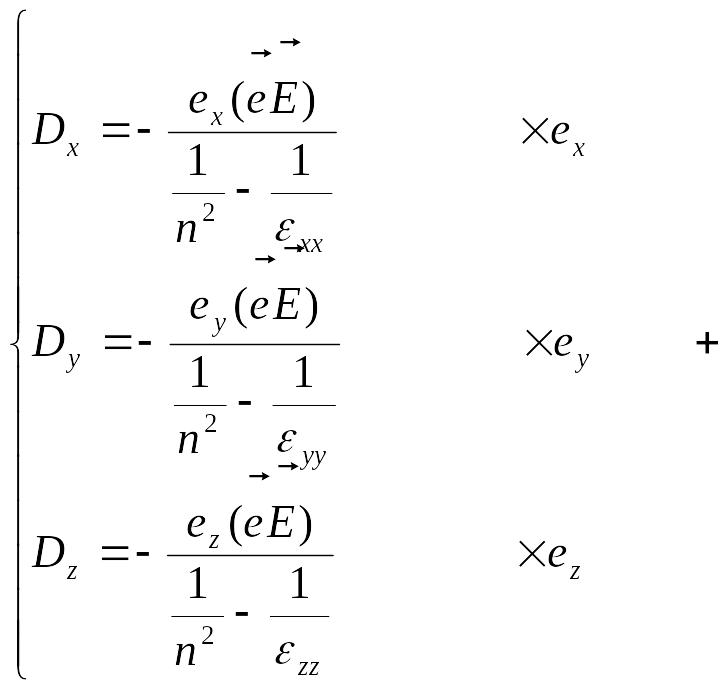
Скалярное
произведение
![]() ,
см. ориентацию векторов. Отсюда:
,
см. ориентацию векторов. Отсюда:
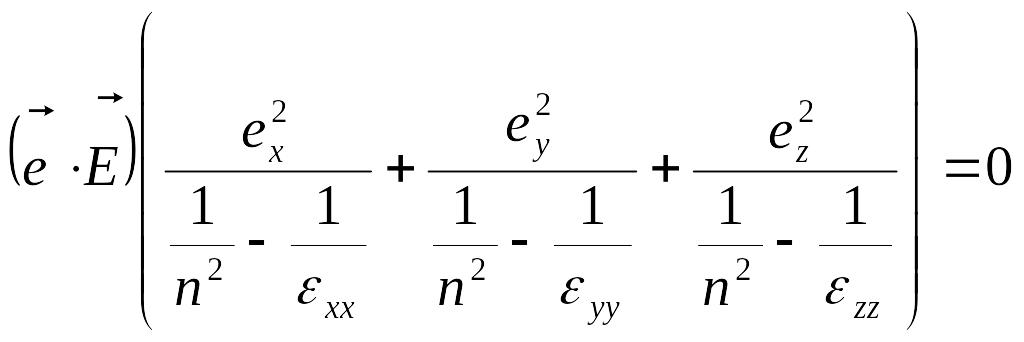 .
.
Уравнение распадается на два
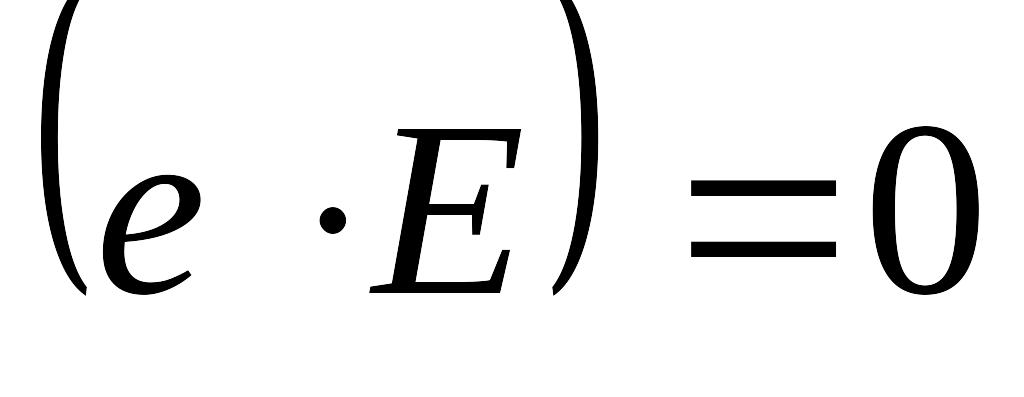 ,
это обыкновенная волна
,
это обыкновенная волнаУравнение нормали Френеля:
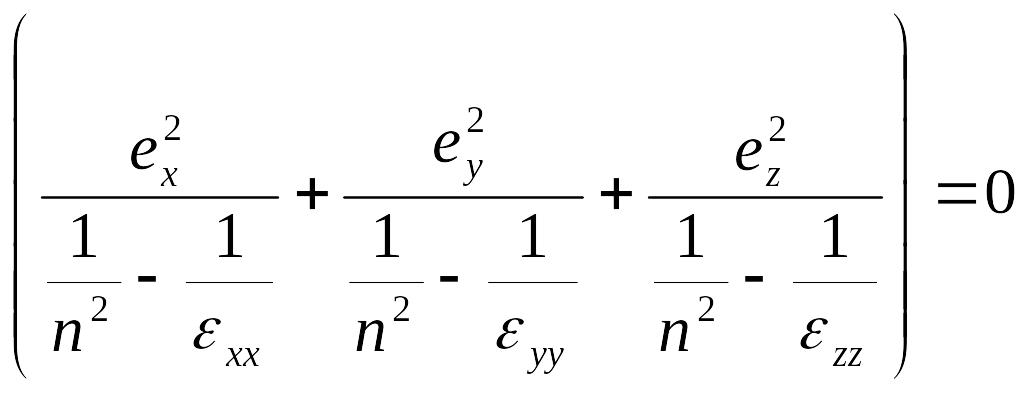
Данное уравнение 4-го порядка, имеет 4 корня, из них разных 2.
Умножим
уравнение на
![]() и получим уравнение для фазовых скоростей:
и получим уравнение для фазовых скоростей:
 .
.
Введем функцию
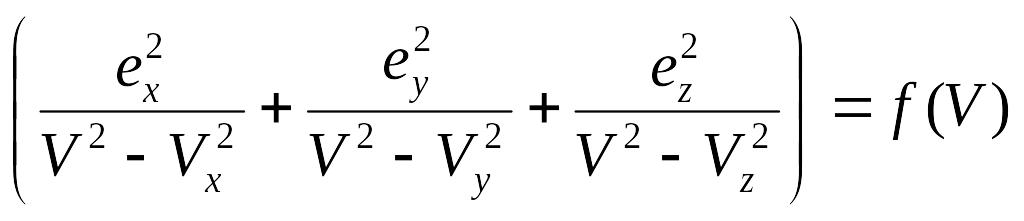
Решим данное уравнение графически.
Получим
две скорости распространения волны в
данном направлении
![]() и
и
![]() .
Покажем что вектора индукции,
соответствующие этим волнам перпендикулярны
между собой,
.
Покажем что вектора индукции,
соответствующие этим волнам перпендикулярны
между собой,
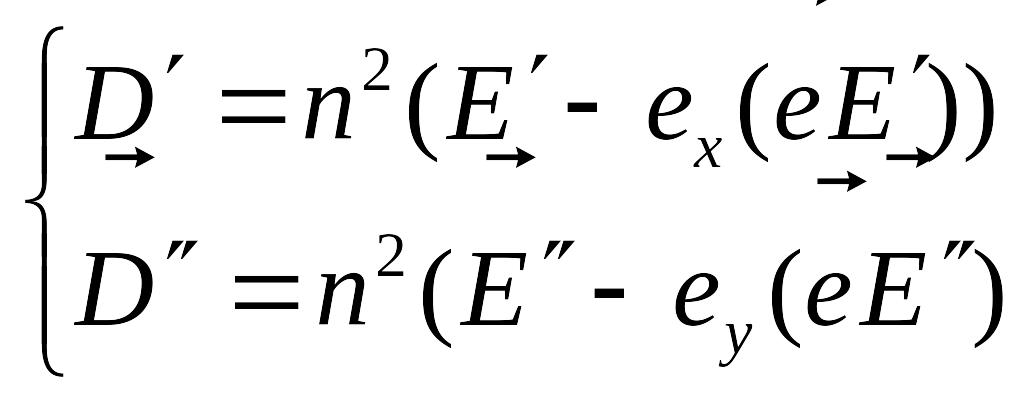 Умножим на
Умножим на
![]() и
вычтем уравнения
и
вычтем уравнения
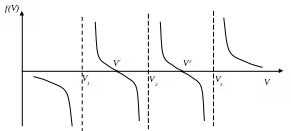
Получим
![]() ,
рассмотрим выражение
,
рассмотрим выражение
![]()
![]() ,
отсюда
,
отсюда
![]() ,
и
,
и
![]()
то
есть
![]() .
.
Пример:
Рассмотрим случай,
![]() ,
т.е.
,
т.е.
![]() ,
уравнение Френеля после приведения к
общему знаменателю имеет вид:
,
уравнение Френеля после приведения к
общему знаменателю имеет вид:
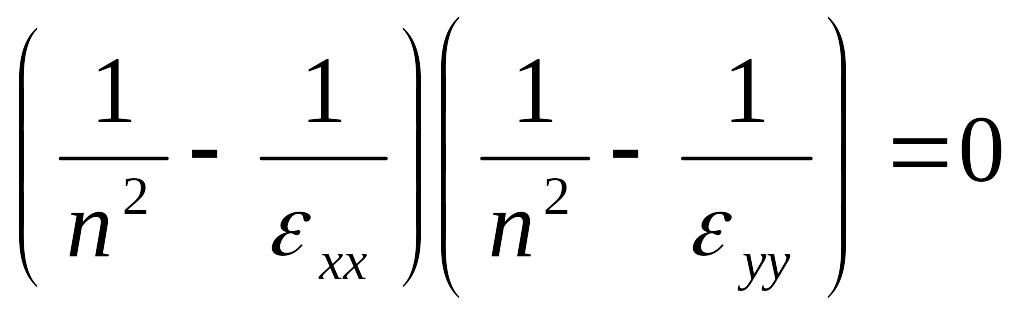 , корни уравнения
, корни уравнения
![]() ,
,
в
данном направлении распространяется
две волны со скоростями
![]() и
и
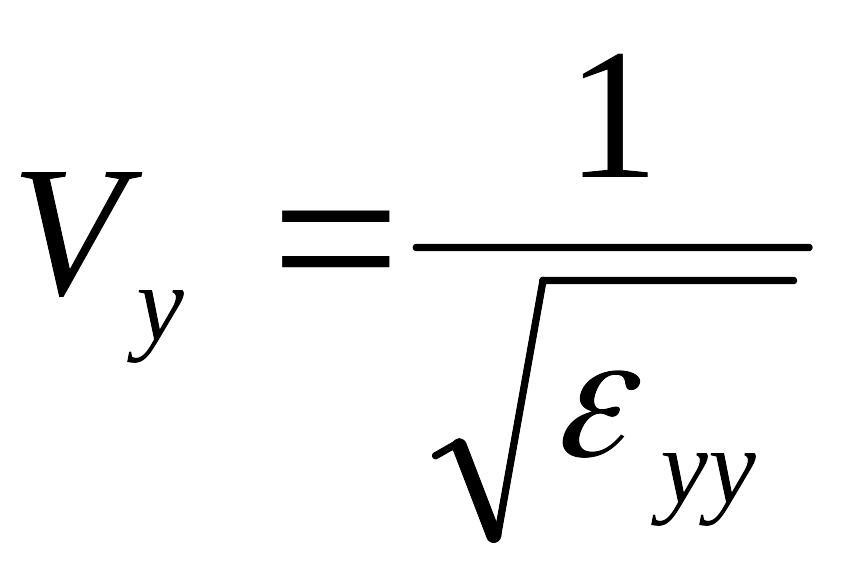 .
.
4.2.4.Уравнение Френеля для лучевых скоростей.
Рассмотрим
распространение энергии (лучей) в
анизотропных средах. Пусть энергия
плоской монохроматической волны
распространяется в направлении,
определяемом единичным вектором потока
энергии
![]() .
.
Уравнения:
умножим векторно на
![]()
![]() .
.
Получим :
![]()
![]() ,
или
,
или
![]() ,
,
получим
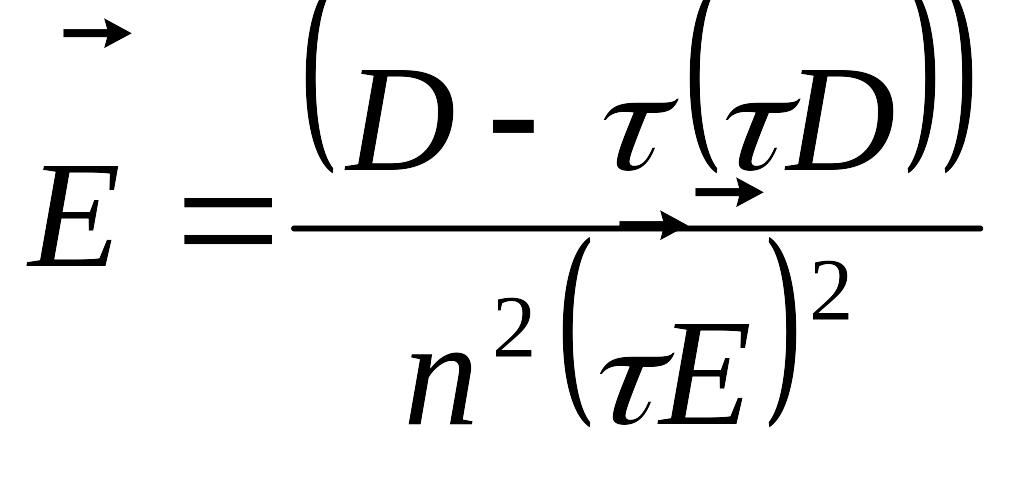 .
.
Умножим
уравнение на
![]() ,
получим
,
получим
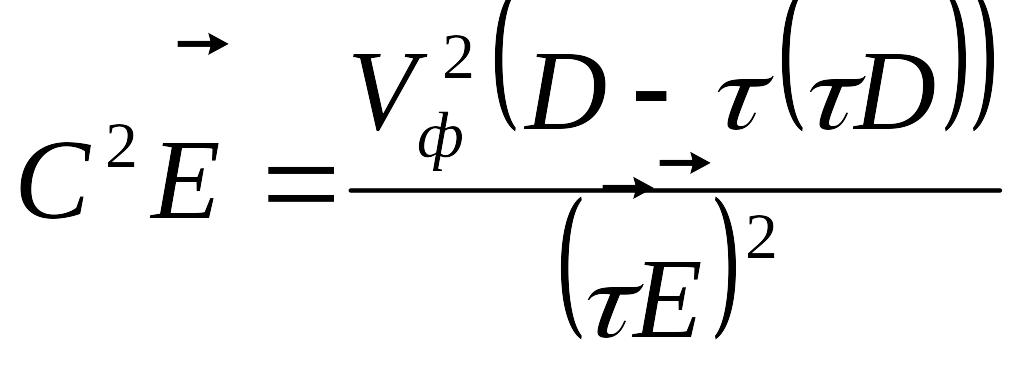 ,
,
так как ,
![]()
Распишем уравнение по компонентам:
![]()
![]()
или
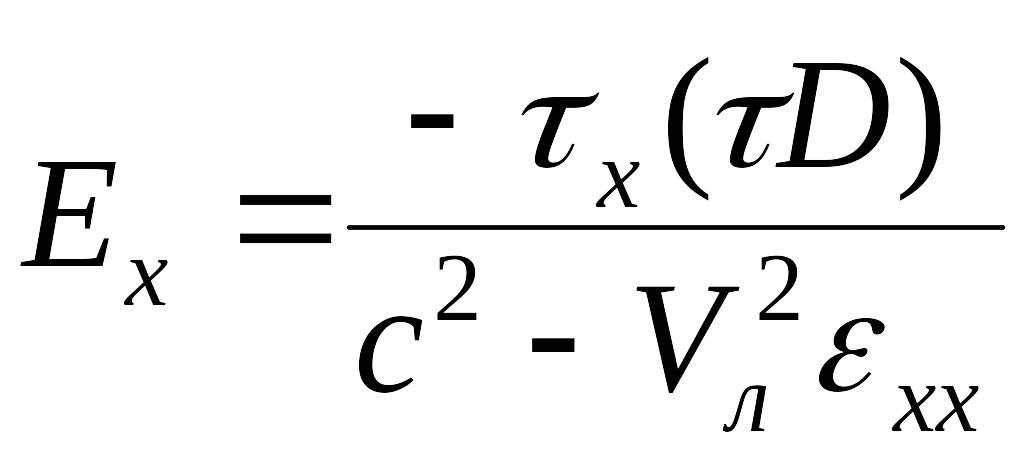 ,
учтем, что
,
учтем, что
![]() ,
получим
,
получим
 +
+
Получаем уравнение Френеля для лучевых скоростей:
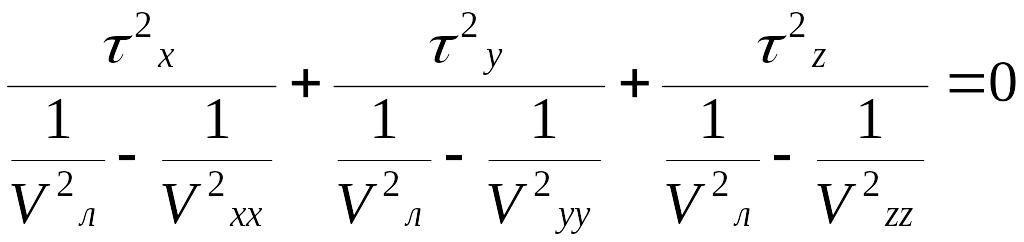
или
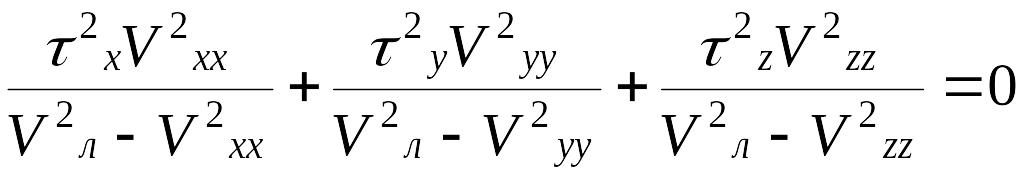
Можно
показать, что
![]() .
.
В
каждом направлении распространяются
2 луча со скоростями
![]() и
и
![]() с
с
4.2.5 Оптические свойства одноосных кристаллов.
В зависимости от структуры кристаллических сред и симметрии тензора диэлектрической проницаемости кристаллы можно разделить на три группы: кубические, одноосные, двуосные.
В
кубических кристаллах
![]() ,
они ведут себя как изотропные среды.
,
они ведут себя как изотропные среды.
В
одноосных кристаллах
![]() ,
,
![]() ,
ось кристалла совпадает с осью (о, Z
)
,
ось кристалла совпадает с осью (о, Z
)
Рассмотрим свойства одноосных кристаллов.
Пусть
![]() ;
;
![]()
Р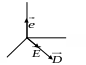 ассмотрим
следующие случаи:
ассмотрим
следующие случаи:
1)
![]()
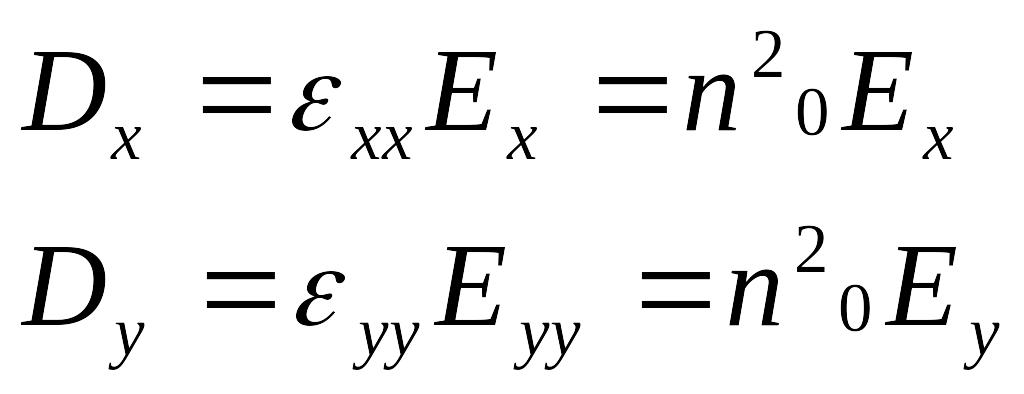
![]() ;
;
![]()
2)Рассмотрим произвольное направление
а)
![]() вектор
вектор
![]() в этом случае лежит в плоскости
в этом случае лежит в плоскости
![]() всегда
всегда
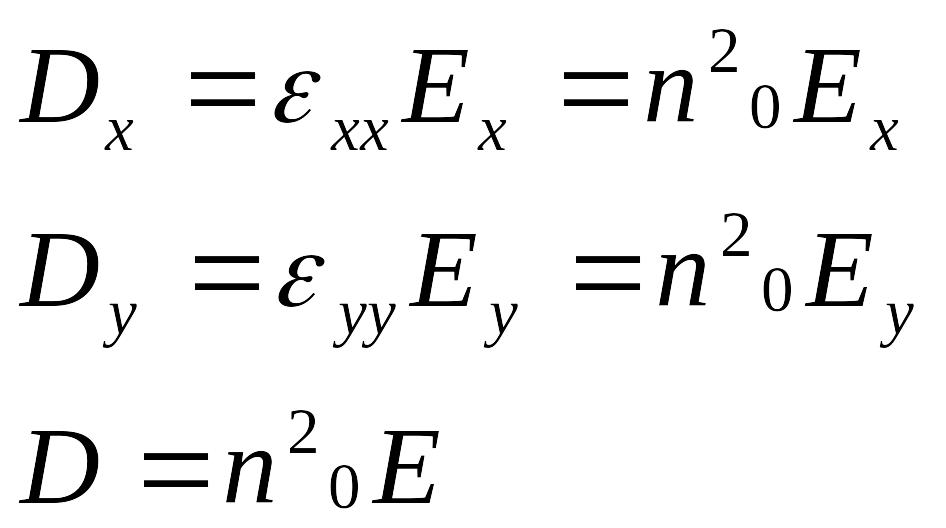
Е
– также
![]()
![]() ,
т. Е. и в этом случае
,
т. Е. и в этом случае
![]()
Уравнение Френеля для одноосного кристалла.
Р ассмотрим
более подробно случай одноосного
кристалла.
ассмотрим
более подробно случай одноосного
кристалла.
Перепишем уравнение Френеля в следующем виде:
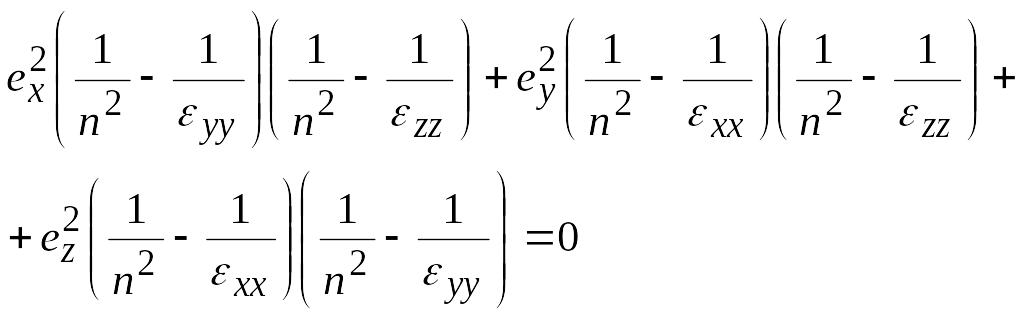
Сделаем преобразования,
учтя, что
![]() ,
введем
и
,
,
введем
и
,
![]() ,
,
![]()
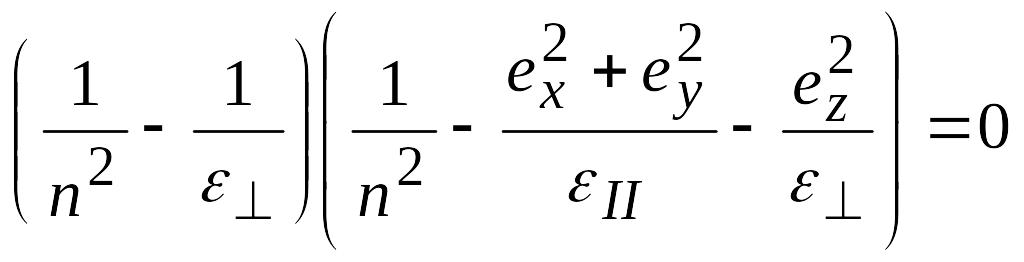
Получим
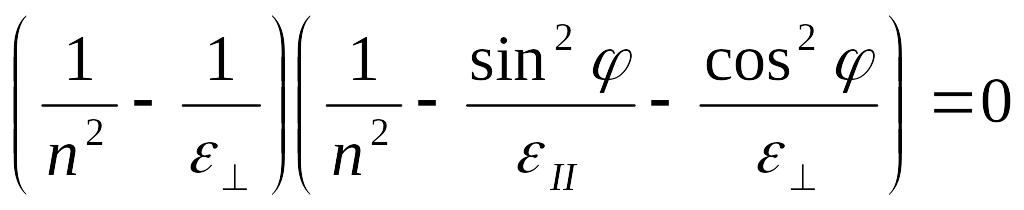
Уравнение распадается на два
1.
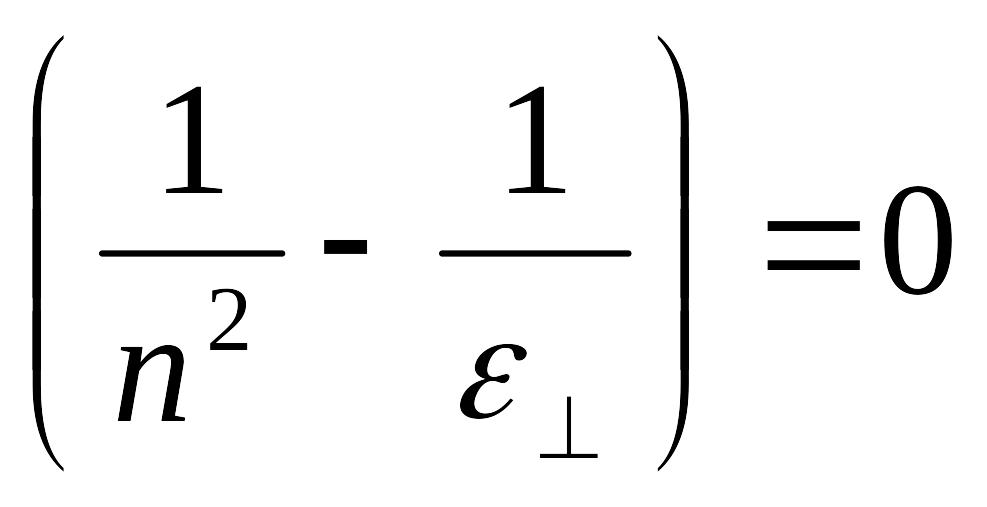
2.
![]()
Уравнение 1 описывает распространение сферической волны для которой показатель преломление не зависит от направления. Такая волна называется обыкновенной. Для волны описываемой уравнением 2 показатель преломления зависит от направления распространения волны, эта волна называется необыкновенной.
Уравнение 2 – уравнение эллипсоида вращения.
При распространении необыкновенной волны:
а) вдоль оси
,
![]() ,
,
![]()
Скорость совпадает со скоростью распространения обычной волны.
б)
![]() оси
оси
![]()
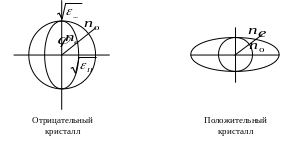 ,
,
![]() ,
,
![]()
Можно построить оптическую индикатрису.
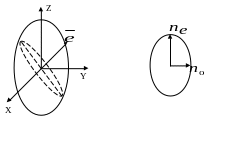
Для нахождения
![]() и
и
![]() строится сечение
строится сечение
![]() ,
тогда в этом сечении главные оси дадут
значения
и
,
а их направления, направления
,
тогда в этом сечении главные оси дадут
значения
и
,
а их направления, направления
![]() и
и
![]()
Уравнение для
лучевых скоростей для одноосного
кристалла будет иметь вид
![]()
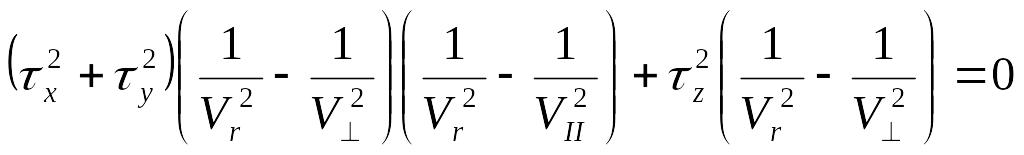
Получаем следующие уравнения:
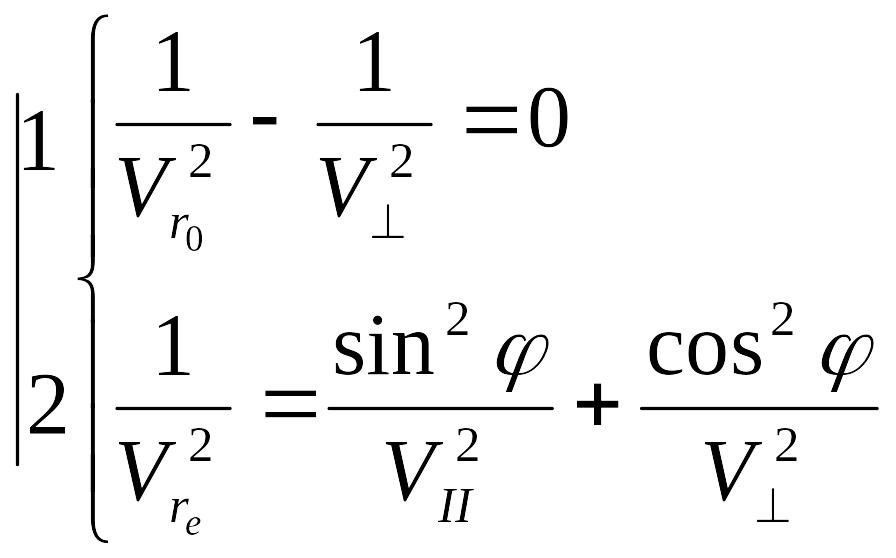
где
![]() и
и
![]() - скорости компонент поляризованных в
главной плоскости и перпендикулярно
главной плоскости соответственно.
- скорости компонент поляризованных в
главной плоскости и перпендикулярно
главной плоскости соответственно.
В каждом направлении
распространяются две волны с лучевыми
скоростями
![]() .
.
Волна, определяемая уравнением 1, имеет
![]() независящую от
направления
независящую от
направления
![]() (обыкновенная
волна)
(обыкновенная
волна)
Волна определяемая уравнением 2 имеет скорость зависящую от направления
В случае ;
![]()
При распространении вдоль оптической оси, скорости обеих волн равны.
Е сли
внутри анизотропной среды расположен
источник – точечный, то волны будут
распространяться следующим образом.
сли
внутри анизотропной среды расположен
источник – точечный, то волны будут
распространяться следующим образом.
