
3267
.pdf
2)F*(х)- неубывающая функция аргумента х;
3)F*(х)=0, если х<х1, и F*(x)=1, если x>xn, где x1 - наименьшее, а хn - наибольшее наблюдаемые значения CВ X .
Из закона больших чисел, а именно из теоремы Бернулли, следует, что при объеме выборки n→∞ ЭФР сходится по вероятности к ТФР. Это означает, что при достаточно большом объеме выборки ЭФР F*(x) и ТФР мало отличаются друг от друга.
Основное значение ЭФР состоит в том, что она используется в качестве оценки ТФР.
Пример. Построить график ЭФР по выборке примера 2. Решение. ЭФР имеет вид
|
0 |
|
x |
15; |
|
|
0,02 |
15 |
x |
25; |
|
|
0,06 |
25 |
x |
35; |
|
F x |
0, 20 |
35 |
x |
45; |
|
0,56 |
45 |
x |
55; |
||
|
|||||
|
0,80 |
55 |
x |
65; |
|
|
0,96 |
65 |
x |
75; |
|
|
1 |
75 |
x. |
|
График F*(x) имеет вид
131
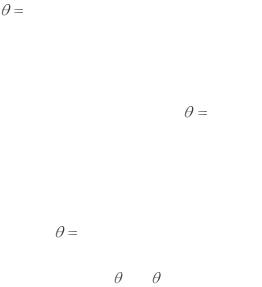
16. СТАТИСТИЧЕСКАЯ ОЦЕНКА НЕИЗВЕСТНЫХ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
16.1. Постановка задачи
При обработке опытных данных часто бывает так, что вид закона распределения генеральной совокупности (ЗРГC) известен, а требуется найти только некоторые параметры, от которых он зависит. Например, если известно, что СВ X распределена по нормальному закону, то на основании опытных данных (по выборке) необходимо "оценить", то есть найти приближенное значение двух параметров - МО и СКО.
Одна из задач математической статистики и состоит в нахождении оценок неизвестных параметров по выборке наблюдений.
Пусть из ГС с ФР F(x,θ), где θ - неизвестный параметр, произведена выборка x1, x2,…,xn объемом п. В качестве оценки параметра θ рассматривают функции элементов выборки
U x1, x2 ,..., xn , которые называются статистиками.
Очевидно, что значения статистик изменяются случайным образом от выборки к выборке или, другими словами, статистики являются СВ U. Задача оценки неизвестного параметра θ сводится к нахождению таких статистик
(выборочных функций) U x1, x2 ,..., xn , которые могут
быть использованы для приближенного определения значения неизвестного параметра θ.
Оценки параметров подразделяются на точечные и интервальные.
Точечная оценка параметра θ определяется одним
числом U x1, x2 ,..., xn .
Интервальной называют оценку, которая определяется двумя числами 1 и 2 - концами интервала, накрывающего оцениваемый параметр θ.
132
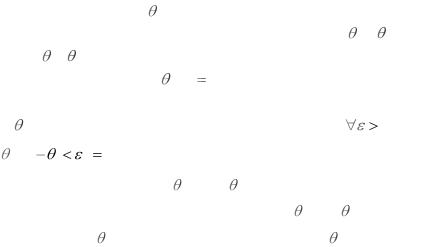
16.2. Основные свойства точечных статистических оценок распределения
Как правило, для оценки параметра можно использовать несколько статистик, получая при этом различные значения оценок. Очевидно, что в качестве оценки следует взять такую статистику, значения которой для различных выборок из данной ГС были бы «в среднем» близки к истинному значению параметра. Желательно также, чтобы с увеличением объема выборки надежность оценки возрастала. Качество оценок характеризуется некоторыми свойствами. Сформулируем основные из них.
Свойство 1. Оценка называется несмещенной, если ее
МО равно оцениваемому параметру, то есть если М( )= . Разность M( )- называется смещением.
Свойство 2. Оценка |
n U x , x ,..., x |
называется |
|
|
1 2 |
n |
|
состоятельной, если при увеличении объема выборки п
оценка |
n |
сходится по вероятности к θ, |
то |
|
есть |
|
0 |
|||||||
|
n |
|
1 . |
|
|
|
|
|
|
|
|
|
||
lim P |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Свойство 3. |
Пусть |
|
и |
|
- |
две |
различные |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
несмещенные |
|
оценки |
параметра |
θ. |
Если |
D( |
|
)<D( |
), |
то |
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
говорят, что оценка 1 более эффективна, чем оценка 2 .
Требование несмещенности устраняет систематические ошибки в определении оценок, обусловленных ограниченным объемом выборки.
Требование состоятельности гарантирует от совершения грубых ошибок ε в определении θ при достаточно большом объема п выборки.
Свойство эффективности используется для выбора оценки, обладающей наименьшим разбросом.
133

Рассмотрим теперь оценки основных числовых характеристик СВ.
16.3.Статистическая оценка МО
Вкачестве статистической оценки МО выбирается выборочное среднее.
Выборочным средним х называется среднее арифметическое элементов выборки
1 n
xn i 1 xi .
Для группированной выборки это соотношение
принимает вид |
|
|
|
|
x |
1 k |
xi ni . |
||
|
|
|||
n i |
||||
|
1 |
|||
Покажем, что выборочное среднее x является несмещенной и состоятельной оценкой. Для этого предварительно заметим, что в теоретических рассуждениях выборку x1, x2,…, xn обычно рассматривают как некоторую реализацию случайного вектора с п независимыми компонентами x1, x2,…, xn, каждая из которых имеет распределение ГС с теми же числовыми характеристиками.
С учетом этого замечания установим несмещенность x :
|
1 |
n |
1 n |
|
1 n |
|
1 |
|
|||
M x M |
|
x M |
|
X |
i |
|
M(X |
) |
|
|
nM(X) M(X) |
|
|
|
|
|
|||||||
|
|
i |
n i 1 |
|
i |
|
|
n |
|
||
|
n i 1 |
|
n i 1 |
|
|
|
|||||
Состоятельность выборочной средней x |
как оценки М(Х) |
||||||||||
с учетом замечания сразу следует из закона больших чисел в форме теоремы Чебышева
|
|
|
|
1 |
n |
|
|
|
|
|
|
||
lim P |
x M X |
lim P |
|
|
xi M X |
1 |
|
||||||
n |
|
n |
|
n i 1 |
|
|
|
|
|
|
|
||
По поводу эффективности x |
заметим, что если CВ X |
|||||
распределена по нормальному закону, то выборочное среднее является эффективной оценкой МО.
134
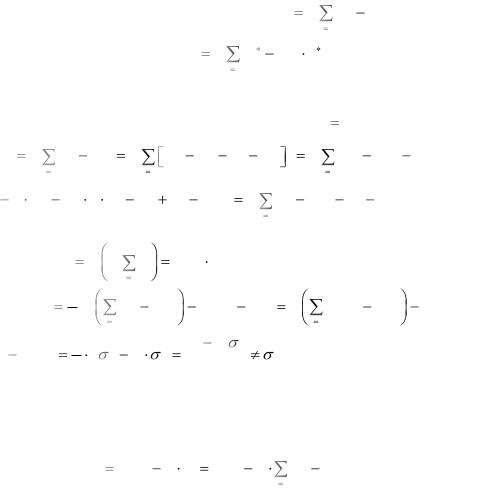
16.4.Статистическая оценка дисперсии
Вкачестве статистической оценки дисперсии D(X) CB
X примем выборочную |
дисперсию |
s2 |
|
1 n |
|
|
2 |
, для |
|||||
|
x x |
||||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
n i |
i |
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
||
группированной выборки |
s2 |
1 k |
x |
|
|
2 |
n . |
|
|
|
|
||
|
|
x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
n i |
i |
|
|
|
i |
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
||
Установим, удовлетворяет ли выборочная дисперсия условиям несмещенности и состоятельности. Предварительно
преобразуем выражение для s2, принимая M[X ] |
m. |
|
|
||||||||||||||||||||||||||||||
|
|
|
1 n |
|
|
2 |
|
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
2 |
1 n |
|
|
|
2 |
|
|||||
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x x |
x m |
|
|
x m |
|
[ x m |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
n i 1 |
i |
|
|
|
|
|
n i 1 |
|
i |
|
|
|
|
|
|
|
|
|
n i |
|
i |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
(*) |
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
||||
|
x m n x m |
x m |
] |
|
|
|
x m |
x m |
, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
n |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n i |
|
i |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
Для проверки несмещенности вычислим M(s2). Так как |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
n |
1/ n2 nD X и D(X)=ζ2 , то |
|
|
|||||||||||||||||||||
|
|
|
D x |
D |
|
|
|
|
|
x |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
M s2 1n M D X 1n n
|
x m 2 |
M X m 2 1 |
M x m 2 |
|||||
n |
|
|
|
|
|
|
|
n |
|
|
i |
|
|
|
|
n |
i |
i 1 |
|
|
|
|
|
|
i 1 |
|
|
1 |
|
n 1 |
2 |
|
|
|
|
2 |
2 |
|
2. |
|
|
|||
|
|
|
|
|
|
|||
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, оценка s2 является смещенной. Для получения несмещенной оценки дисперсии выборочную дисперсию s2 исправляют, умножая ее на множитель n/(n-1).
Исправленная дисперсия
s2 |
n / n 1 s2 1/ n 1 |
n |
2 |
x x |
|||
0 |
|
i |
|
|
|
i 1 |
|
является уже несмещенной оценкой дисперсии.
Покажем, что оценка s2 (а вместе с ней и s02 )
состоятельна. Для этого воспользуемся равенством (*). Первый член в правой части равенства (*) является средним
135

арифметическим п независимых, одинаково распределенных СВ (хi-m)2. Согласно закону больших чисел
1 |
n |
|
2 |
p |
2 |
|
2 . |
|
|
|
|||||
|
X |
m |
|
M X m |
|
D X |
|
|
|
|
|||||
n i 1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Второй член равенства (*) ( x -m)2 - квадрат величины, стремящейся по вероятности к нулю (по закону больших чисел), тоже стремится к нулю. Отсюда s2 является суммой двух слагаемых, одно из которых стремится к ζ2, то есть
p
s2 2 n
Итак, мы рассмотрели оценки неизвестных параметров распределения по выборке для частного случая, когда оцениваемый параметр θ является математическим ожиданием или дисперсией распределения, то есть первым начальным и вторым центральным моментами распределения. Рассмотрим теперь общие методы нахождения точечных оценок.
16.5. Метод моментов
Пусть известен вид распределения ГС F(x, θ1, θ2,..., θk), зависящего от k параметров. Идея метода моментов заключается в следующем: по выборке вычисляют k выборочных моментов и приравнивают их к cooтветствующим моментам распределения ГС. Искомые оценки каждого из k параметров находятся как решение полученной системы k уравнений. При этом оценки начальных и центральных моментов k-гo порядка вычисляются по формулам
|
|
1 n |
|
|
1 n |
|
k |
||
k |
|
xk , |
|
k |
|
|
x x |
|
|
|
|
|
|
||||||
|
|
i |
|
n i 1 |
i |
|
|||
|
|
n i 1 |
|
|
|
|
|||
Замечание. |
Оценки |
математического ожидания и |
|||||||
дисперсии, рассмотренные выше, получены по методу моментов.
Пример. СВ Х распределена по показательному закону с плотностью вероятностей f(x,θ)=θe-θx. Требуется по
136

результатам наблюдений х1, х2,…, хп оценить параметр θ. Решение. Ранее мы находили М(Х)=α1=1/θ. Оценка
математического ожидания есть выборочное среднее
1 |
|
1 |
n |
|
|
x |
|
xi . Приравнивая |
теоретический момент α1 |
||
|
|||||
|
|
n i 1 |
|
|
|
эмпирическому 1 , получаем1/ |
x1 . Отсюда |
||||
|
|
|
|
|
n |
|
|
|
1/ x |
n / |
xi . |
|
|
|
|
i |
1 |
Метод моментов обладает тем недостатком, что оценки, полученные по нему, вообще говоря, не являются асимптотически эффективными и могут быть смещенными.
16.6. Метод максимального правдоподобия
Метод максимального правдоподобия наиболее распространен при нахождении точечных оценок параметров. Будем рассматривать результаты выборки как реализацию n- мерной случайной величины (x1, х2,..., хп) с независимыми компонентами. Для получения оценки неизвестного параметра
θ естественно попытаться найти такое значение , при котором вероятность реализации этой выборки x1, х2,..., хп была бы максимальной.
Если СВ X дискретна, то закон распределения ее имеет вид P(X=хi)=pi(θ), i=1,2,...,n. Тогда вероятность при п независимых наблюдениях CВ X получить выборку (x1, х2,..., хп) равна
L |
L x1, x2 ,..., xn |
P X1 |
x1, X2 |
x2 ,..., Xn |
xn |
|
P |
X1 x1 P X2 |
x2 , P Xn |
xn |
p1 |
p2 |
... pn . |
|
Функция L(θ) |
называется функцией правдоподобия, а |
||||
величина , являющаяся точкой максимума этой функции, есть оценка параметра θ, полученная по методу максимального правдоподобия (сокращенно МП-оценкой).
137

Если определяется оценка непрерывной CВ X с плотностью распределения f(x,θ), то функция правдоподобия определяется так:
L |
L x1 , x2 ,..., xn , |
f x1 , |
f x2 , |
f xn , . |
Если функция правдоподобия дифференцируема по θ и при любых возможных значениях xi достигает максимума по θ
внутри интервала возможных значений параметра θ, то находят, решая уравнение
L x1, x2 ,..., xn |
, |
0 |
|
|
Поскольку точки максимума функции L x1, x2 ,..., xn ,
и ln L x1, x2 ,..., xn , при фиксированных х1,..., хn совпадают, то в некоторых случаях удобно решать уравнение
ln L x1, x2 ,..., xn |
, |
0. |
|
|
Если требуется оценить не один, а k неизвестных параметров θ1,θ2,…,θk, то оценки максимального правдоподобия для этих параметров находят, решая систему уравнений
L x1, x2 ,..., xn |
, 1 |
,..., k |
0, |
j 1,2,..., k. |
|
|
|
j
Ценность МП-оценок обусловлена следующими их свойствами, которые выполняются при весьма общих условиях. Приведем их без доказательства для случая одного параметра.
1. Уравнение правдоподобия имеет решение, которое является состоятельной оценкой параметра θ.
2.Решение является асимптотически эффективной оценкой для θ.
3.Решение имеет асимптотически нормальное
138

предельное распределение, то есть при соответствующей нормировке предельное распределение при n→∞ полученной оценки оказывается нормальным.
4.Если для параметра θ существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой.
Недостатками метода является то, что МП-оценка может оказаться смещенной, а также то, что этот метод на практике нередко приводит к довольно сложным системам уравнений.
Пример. Пусть СВ Х распределена по нормальному закону N(m,ζ2) с неизвестными параметрами m и ζ2. Найти
МП-оценку |
параметра |
параметров |
нормального |
распределения. |
|
|
|
Решение. Рассмотрим |
выборку x1, |
x2,…, xn как |
|
реализацию n-мерного СВ (Х1, Х2,…, Хn). Тогда составляющие Хi также распределены по закону N(m,ζ2). Запишем функцию правдоподобия
|
|
1 |
|
|
|
1 |
n |
2 |
|
|
L x1, x2 ,..., xn , m, |
2 |
|
exp |
|
xi m |
. |
||||
|
|
|
n |
|
2 |
|
||||
|
|
2 |
2 |
i 1 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
Здесь удобнее перейти к ln L :
ln L |
x1, x2 ,..., xn , m, |
2 |
n / 2 |
ln |
2 |
n / 2 |
ln |
2 |
|||||
|
|
||||||||||||
|
n |
|
|
|
|
2. |
|
|
|
|
|
. (**) |
|
1/ 2 |
2 |
|
x m |
|
|
|
|
|
|
||||
|
|
|
i |
|
|
|
|
|
|
|
|
||
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
Дифференцируя (**)по m и ζ2, получаем систему |
|||||||||||||
|
|
|
ln L |
|
1 |
xi m |
0; |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
m |
|
2 |
|
|
|
|||||
|
|
|
|
i 1 |
|
|
|
|
|
||||
|
|
|
ln L |
|
|
|
1 |
n |
x m 2 |
|
|
||
|
|
|
|
|
n / 2 2 |
|
|
0. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
2 4 |
|
i |
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|||
|
|
|
|
|
|
|
|
139 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
Из первого уравнения находим m |
1/ n |
xi |
x . |
Подставив |
||||||
|
|
|
|
|
|
i 1 |
|
|
|
|
это |
значение |
|
во |
второе |
уравнение, |
получим |
||||
2 |
1/ n |
x |
|
2 . Заметим, что |
оценка |
m |
совпадает |
с |
||
x |
||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
оценкой, полученной по методу моментов, |
а оценка 2 |
не |
||||||||
совпадает. |
|
|
|
|
|
|
|
|
||
|
17. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ НЕИЗВЕСТНЫХ |
|
||||||||
|
|
ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ |
|
|
||||||
|
|
17.1. Доверительный интервал и доверительная |
|
|||||||
|
|
|
|
|
вероятность |
|
|
|
|
|
|
В |
предыдущей |
главе были |
рассмотрены |
точечные |
|||||
оценки неизвестных параметров распределения. За
исключением редких случаев оценка не совпадает с истинным значением θ оцениваемого параметра, то есть всегда
имеет место некоторая ненулевая погрешность . Часто точное значение погрешности несущественно, а требуется лишь знать, что она находится в определенных пределах. На основании выборки x1, x2,…, xn указывают два значения
θ1(x1, x2,…, xn) и θ2(x1, x2,…, xn), c помощью которых можно сделать статистический вывод о том, что истинное значение
параметра θ лежит в интервале ]θ1, θ2[.
Доверительным интервалом для параметра θ называется интервал ]θ1, θ2[, содержащий истинное значение параметра с заданной вероятностью р=1-α. Таким образом,
P(θ1<θ<θ2)=1-α. |
(1) |
|
Число 1-α называется |
доверительной вероятностью |
|
(надежностью), а значение α - уровнем значимости. |
|
|
Нижняя и верхняя границы доверительного интервала θ1 |
||
и θ2 определяются по |
результатам наблюдений |
и, |
следовательно, являются случайными величинами. В связи с этим говорят, что доверительный интервал накрывает
140
