
3267
.pdf
MX,Y x, y f x, y dxdy .
12.3.Свойства математического ожидания
1.М(с)=с, где с - постоянная.
2.М(сХ)=сМ(Х), где с - постоянная.
Эти свойства следуют из соответствующих свойств интеграла или ряда.
3. Свойство аддитивности.
М(X+Y)=М(Х)+M(Y), если М(|Х|), М(|Y|) конечны.
Доказательство проведем отдельно для случаев дискретной и непрерывной СВ.
a) (X,Y) - дискретная двумерная СВ. Пусть X принимает значения x1,х2,..., a Y - значения y1,у2,.… Тогда СВ Z=X+Y принимает значения z1,z2,..., где все zk=xi+уj. различны, а
P Z |
zk |
P X |
Y |
zk |
|
pij , |
pij=P(X=xi, Y=yj), |
|||
|
|
|
|
|
i, j :xi |
y j |
zk |
|
|
|
M X Y |
zk P Z zk |
zk |
|
|
pij |
|
||||
|
|
|
k 1 |
|
k 1 |
i, j :xi |
y j |
zk |
|
|
|
|
|
xi |
y j |
pij |
xi |
y j pij |
xi |
pij |
|
k 1 i, j :xi |
y j |
zk |
|
i, j 1 |
|
|
|
i 1 |
j 1 |
|
yi |
pij |
|
xi pi |
y j pij |
M X M Y . |
|
||||
j 1 |
i 1 |
|
i 1 |
|
j 1 |
|
|
|
|
|
Здесь были введены обозначения |
|
|
|
|||||||
|
pij |
|
P X xi |
pi , |
pij |
P Y y j |
pij . |
|||
j |
1 |
|
|
|
i |
1 |
|
|
|
|
б) Пусть (X,Y) - непрерывная двумерная CВ c плотностью распределения вероятностей f(х,у). Плотность распределения суммы Z=X+Y имеет вид
f z f x, z x dx ,
поэтому
111
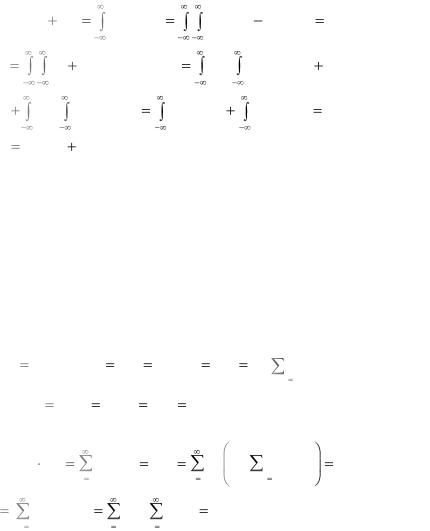
M X Y |
|
zf z |
dz |
zf x, z |
x |
dxdz |
||
x |
y |
f |
x, y |
dxdy |
xdx f |
x, y |
dy |
|
ydy |
f |
x, y |
dx |
xf |
x dx |
yf |
y |
dy |
M X M Y .
Интегралы можно переставлять в силу их абсолютной сходимости.
Следствие. Из свойств 2,3 вытекает свойство линейности математического ожидания
М(с1Х+с2Y)=с1М(Х)+c2(Y).
4.Свойство мультипликативности. Еcли СВ X и Y независимы, то M(ХY)=М(Х)M(Y) при условии, что M(|Х|), М(|Y|) конечны.
а) Пусть Z=XY - дискретная СВ со значениями z1, z2,..., где вcе zk различны:
zk xi y j , P Z zk P XY zk |
pij , |
i, j :xi y j |
zk |
pij P X xi , Y y j pi q j . |
|
Так как X и Y независимы, то |
|
M X Y |
zk P Z zk |
zk |
pi q j |
|
k 1 |
|
k 1 |
|
i, j :xi y j zk |
xi y j pi q j |
xi pi |
y j q j |
M X M Y . |
|
i, j 1 |
i 1 |
j 1 |
|
|
Группировка рядов законна в силу их абсолютной сходимости.
б) (X,Y) - непрерывная двумерная CB c плотностью распределения f(x,y)=f(x)f(y). Плотность распределения CB Z=XY была найдена. C учетом независимости CВ X и Y имеем
112

|
|
|
|
|
f z |
0 |
1 |
|
f x f z / x dx |
|
1 |
|
f x f z / x dx . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x |
0 |
x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M XY |
|
zf |
z |
dz |
0 |
1 |
|
f x |
dx |
zf |
z / x |
dz |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z / x |
t; |
|
|
z / x |
t |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
f |
x |
dx |
zf |
z / x |
dz |
|
|
|
z |
|
|
, |
t |
; |
z |
, |
t |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 x |
|
|
|
|
z |
|
, |
t |
|
|
; |
z |
, |
t |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
x |
|
0; |
|
0 |
x |
|
|
||
0 |
1 |
f |
|
x dx |
x |
2tf |
t |
dt |
|
1 |
|
f |
x |
dx |
|
|
x2tf |
t |
dt |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x |
|
0 |
|
x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
xf |
x |
dx |
tf |
t |
dt |
M X M Y . |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
Перестановки интегралов законны в силу их |
||||||||||||||||||||||
абсолютной сходимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
5. Некоторые неравенства. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
а) Если X≥Y, то М(Х)≥M(Y). |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Действительно, |
CB |
|
|
|
|
Z=X-Y≥0, |
потому |
согласно |
||||||||||||||
определению математического ожидания получаем свойство
5а;
б) M(|XY|)≤ 
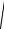 M X2 M Y 2 - неравенство Коши-
M X2 M Y 2 - неравенство Коши-
Буняковского;
в) Р(|X|>ε)≤M(|X|)/ε, если M(|Х|) конечно (первая форма неравенства Чебышева).
Для доказательства введем случайную величину Y по формуле
0, |
если |
Х |
, |
Y |
|
|
|
, |
если |
Х |
. |
|
|
|
|
113

Таким образом, Y – дискретная СВ, принимающая два
значения: 0 с вероятностью Р(|X| |
) и |
с вероятностью |
||||
P(|X| |
). |
|
|
|
|
|
Из определения Y следует, что Y≤|X|, и в силу 5а имеем |
||||||
M (Y) |
0 P(|X| |
) + |
P(|X|> |
) ; M(|X|)≥M(Y)=εP(|X|>ε), |
||
что совпадает с 5в. В частности, если Х≥0 и |
М(Х), то |
|||||
|
|
Р(Х≥ε)≤М(Х)/ε. |
|
|
||
Пример. |
Найти |
математическое |
ожидание |
|||
биномиального распределения. Используем при этом свойство
3.
Решение. Рассмотрим СВ μ, равную числу успехов в п испытаниях в схеме Бернулли с вероятностью успеха р в каждом испытании. СВ μ распределена по биномиальному закону. Обозначим через Аi событие, состоящее в том, что в i-м испытании произошел успех. Тогда СВ μ можно представить в виде
|
|
|
|
|
А |
А |
|
... |
А , |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
п |
|
|
|
где |
Аi |
- индикатор |
|
события |
Ai. |
Для |
математического |
|||||
ожидания СВ μ получаем |
|
|
|
|
|
|
|
|||||
|
|
|
n |
|
|
|
n |
|
|
|
||
|
|
M |
|
|
M |
A |
|
P Ai |
np . |
|
||
|
|
|
i |
1 |
i |
|
i 1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
Пример. Вычислить МО в гипергеометрическом |
|||||||||||
распределении (урновая схема). |
|
|
|
|
|
|||||||
|
|
|
|
|
Ck |
Cn k |
|
|
|
|
|
|
|
|
P X |
k |
|
M |
N M |
|
, |
k |
0,1,..., n |
|
|
|
|
|
Cn |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
Рассмотрим урновую схему. Пусть в урне N шаров, из |
|||||||||||
них М белых, п - объем выборки. |
|
|
|
|
|
|||||||
|
Пусть Х-СВ - число белых шаров в выборке объемом n, |
|||||||||||
Ai |
- |
событие |
"i-шар |
выборки |
белый". |
Тогда |
||||||
Х |
А1 |
... |
и по свойству 3 аддитивности |
|
||||||||
|
А2 |
Ап |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
М Х |
1 P Ai . |
|
|
||||||
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
114 |
|
|
|
|
||

Так как P(Ai)=М/N при любом i, то М(Х)=пМ/N.
13.ЗАКОН БОЛЬШИХ ЧИСЕЛ
13.1.Закон больших чисел
Стандартное теоретико-вероятностное заключение - вероятность события А равна р - на позволяет, как правило, предсказать, произойдет событие А или нет. Исключение составляют лишь те случаи, когда р либо очень мало, либо очень близко к единице. При этом можно утверждать, что событие А практически невозможно или соответственно практически достоверно.
Ниже будет рассмотрен ряд результатов теории вероятностей, известных под названием "закон больших чисел" и позволяющих делать подобные предсказания. Всякое утверждение о малости некоторой величины естественно формулировать в терминах предельного перехода. Введем понятие сходимости СВ по вероятности.
Последовательность СВ X1,Х2,...,Хп
сходящейся по вероятности при п→∞ к СВ X, если
lim P |
|
Xn X |
|
0 Xn |
p |
X при n |
. |
(1) |
|
|
|||||||
|
|
|
||||||
n |
|
|
|
|
|
|
|
|
Этот тип сходимости означает, что, каково бы ни было число ε>0, найдется число N, такое, что n N вероятность выполнения неравенства |Xn-X|≥ε будет сколь угодно малой, иначе, событие |Xn-X|≥ε будет практически невозможным.
Доказательства теорем, составляющих содержание закона больших чисел, основаны на втором неравенстве Чебышева, которое сформулируем как утверждение (второе неравенство Чебышева).
Если СВ X имеет дисперсию D(X), а ε - произвольное число, то справедливо неравенство
115

|
|
|
|
|
D X |
. |
(2) |
||
P |
X M X |
|
|||||||
|
|
2 |
|||||||
Известно первое неравенство Чебышева для |
|||||||||
положительной СВ Y |
|
|
|
|
|
|
|
|
|
|
P Y |
|
|
|
M Y |
. |
|
||
|
|
|
|
|
|
||||
Положив Y=|X-M(X)|2 |
и δ=ε2 и учитывая, |
что |
|||||||
M(X-M(X))2=D(X), получаем неравенство (2).
Основываясь на втором неравенстве Чебышева, можно сформулировать удобный критерий сходимости по вероятности.
Если для последовательности СВ {Хn} |
М(Хn)=0 |
и |
||||||||
D(xn)→0 при п→∞, то Хп |
р |
0 . |
|
|
|
|
||||
|
|
|
|
|
||||||
В силу неравенства (2) и того, что M(Xn)=0 |
0 , |
|||||||||
имеем |
|
|
|
|
|
|
|
|
||
0 P |
|
X |
n |
|
D Xn |
при |
п |
, |
|
|
|
|
|
||||||||
|
|
|
|
|
||||||
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
а это означает, что |
|
р |
0 при п→∞. |
|
|
|
||||
Хп |
|
|
|
|||||||
Перейдем теперь к формулировке закона больших чисел |
||||||||||
в форме Чебышева. |
|
|
|
|
|
|
|
|
||
Теорема |
Чебышева. |
|
Пусть |
Х1,Х2,...,Хп |
- |
|||||
последовательность попарно независимых СВ, дисперсии
которых ограничены в совокупности, т.е. D(Xi)≤C, |
i=1, 2,..., |
||||||
где С - некоторая постоянная. Тогда |
0 . |
|
|||||
|
1 |
n |
1 n |
|
1. |
(3) |
|
|
|
||||||
lim P |
|
Xi |
|
M Xi |
|
||
|
|
||||||
n |
n i 1 |
n i 1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Другими словами, при выполнении условий теоремы последовательность средних арифметических п СВ сходится по вероятности к среднему арифметическому их математических ожиданий. Действительно,
116
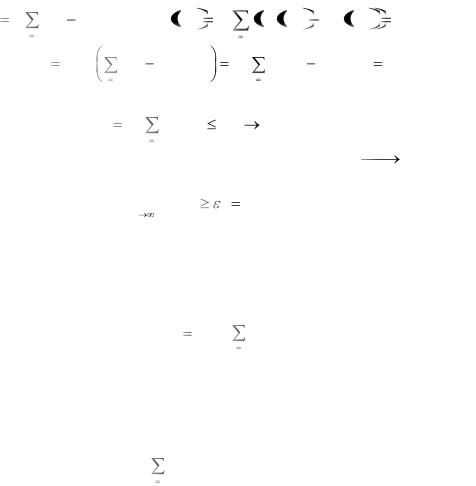
Yn |
|
1 n |
Xi M Xi , |
|
M Yn |
|
|
1 n |
|
M Xi |
|
M Xi |
|
0 , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
n i 1 |
|
|
|
n i 1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|||||
|
D Y |
|
|
D |
X |
i |
|
M X |
i |
|
|
|
|
|
|
D X |
i |
M X |
i |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
n |
|
n2 |
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
nC |
|
|
0 . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
i 1 D Xi |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
n2 |
n2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
Отсюда на основании критерия сходимости Yn |
p |
0 |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
при п→∞, то еcть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
lim P |
Yn |
|
|
0 . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переходя к противоположному событию, получаем |
|||||||||||||||||||||||
равенство (3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Следствие. Пусть при выполнении условий теоремы |
|||||||||||||||||||||||
Чебышева СВ X1,X2,...,Xп |
имеют одинаковые математические |
|||||||||||||||||||||||||
ожидания |
М(Х1)=М(Х2)=…=т. |
Тогда |
последовательность |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
средних арифметических |
Yn 1/ n |
Xi |
при п→∞ сходится |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
||
по вероятности к т. Это следствие может быть истолковано следующим образом.
Пусть имеется СВ X, которая в результате п испытаний принимает значения Х1,Х2,...,Хп. Эти значения можно рассматривать как СВ, распределенные по тому же закону, что
|
1 |
n |
и СВ X. В этом случае |
|
Xi есть среднее арифметическое из |
|
||
|
n i 1 |
|
всех возможных значений СВ X, a m - М(Х). Тогда следствие означает, что при п→∞ среднее арифметическое из значений СВ X сходится по вероятности к ее математическому ожиданию.
Важнейшим следствием закона больших чисел Чебышева является следующая теорема.
Теорема Бернулли. Относительная частота успехов в п независимых испытаниях по схеме Бернулли сходится по
117
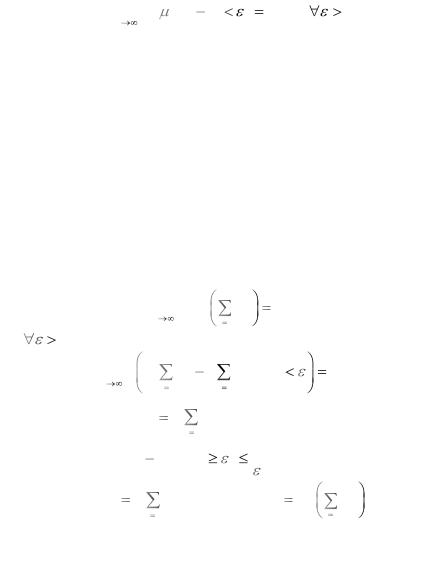
вероятности при п→∞ к вероятности р успеха в одном испытании, то есть
lim P |
n / n p |
1 |
0 , |
(4) |
n |
|
|
|
|
где μn - число успехов в п испытаниях.
Для доказательства этой теоремы воспользуемся представлением этой величины μn в виде суммы п индикаторов: μn=χ1+χ2+…+χп. Мы уже вычислили МО и дисперсии СВ Xk. М(Хk)=p, а D(Xk)=pg. Таким образом, СВ Хk имеют одинаковые МО и ограниченные дисперсии. (1/п)(χ1+χ2+…+χп)=μп/п есть относительная частота успеха в п испытаниях. Отсюда из следствия к теореме Чебышева получается соотношение (4).
Закон больших чисел может быть сформулирован и для зависимых СВ.
Теорема Маркова (закон больших чисел в общей формулировке). Если дисперсии произвольных СВ в последовательности Х1,Х2,…,Хп удовлетворяют условию
|
|
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|||
|
|
|
|
|
lim |
D |
Xi |
|
0 , |
|
|
|||||||||
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
n |
n |
|
|
|
i 1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то |
0 выполняется предельное соотношение (3) |
|||||||||||||||||||
|
|
|
|
|
n |
|
|
|
1 |
n |
|
|
|
|
1 . |
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
lim P |
|
|
|
|
Xi |
|
|
|
M Xi |
|
|
|
|
||||||
|
|
|
n i 1 |
|
|
|
|
|
|
|
||||||||||
|
n |
|
|
|
|
|
|
|
n i 1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Обозначим |
Yn |
|
1 n |
Xi |
и воспользуемся неравенством |
||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
n i 1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||
Чебышева (2) P |
Y |
M Y |
|
|
|
D Y |
и тем, что |
|||||||||||||
|
|
|
2 |
|
||||||||||||||||
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
n |
|
|||||
|
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
||||
|
M Yn |
|
i 1 M Xi |
|
|
|
и D Yn |
|
|
|
i 1 Xi . |
|||||||||
|
n |
|
|
|
|
|
n2 |
|||||||||||||
Тогда для вероятности противоположного события находим оценку
118

|
1 n |
1 n |
|
1 |
n |
||
P |
|
i 1 Xi |
|
i 1 M Xi |
1 |
|
D i 1 Xi . |
n |
n |
2n2 |
|||||
Переходя к пределу и учитывая условия (5), получаем соотношение (3).
13.2. Центральная предельная теорема (теорема Ляпунова)
Утверждения, полученные в форме закона больших чисел, представляют собой заключения о сходимости последовательности СВ {Хn}, п=1,2,...,k к некоторой случайной (или неслучайной) величине X. Эти утверждения не дают нам никакой информации о том, как аппроксимировать распределение СВ Хп при больших п. Ответ на этот вопрос дают так называемые предельные теоремы, в которых речь идет о новом виде сходимости последовательности СВ - сходимости по распределению.
Теорема (центральная предельная теорема в упрощенной формулировке). Если Х1,Х2,…,Хп - независимые одинаково распределенные СВ, имеющие математические ожидания M(Xi)=m и дисперсии D(Xi)=ζ2, то при n→∞ ФР нормированной суммы
n
Xi m
Y i 1
 n
n
сходится к ФР нормальной СВ с параметрами (0,1), то есть при любых х
|
|
1 |
x |
t2 |
|
P Y x |
F x |
|
dt . |
||
|
e |
|
|||
|
|
|
|
2 |
|
n |
Yn |
2 |
|
|
|
|
|
|
|
|
Следствиями центральной предельной теоремы являются две предельные теоремы, рассмотренные ранее и относящиеся к схеме Бернулли: интегральная теорема Муавра-Лапласа, локальная теорема Муавра-Лапласа,.
119
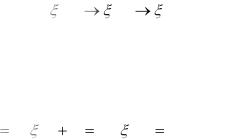
14.ЦЕПИ МАРКОВА
14.1.Определения. Примеры
Пуассоновский процесс, рассмотренный ранее, является частным случаем стохастических процессов без последствия, или процессов Маркова. Сейчас мы рассмотрим другой частный случай марковских процессов, когда параметр принимает лишь дискретную последовательность значений. Такие марковские процессы с дискретным временем называют
цепями Маркова.
Условно будем говорить о некоторой системе, шаг за шагом меняющей свое фазовое состояние. Будем считать, что имеется лишь конечное или счетное число различных фазовых состояний е1,е2,….
Обозначим через ξ(п) состояние системы через п шагов. Будем предполагать, что цепочка последовательных переходов
0 |
1 |
2 ... |
зависит от вмешательства случаев, причем соблюдается следующая закономерность: если на каком-либо шаге п система находится в состоянии еi, то, независимо от предшествующих обстоятельств, она на следующем шаге с вероятностью pij переходит в состояние еj:
pij P |
n 1 e j / n ei , i,j=1,2,…. |
Описанная модель и называется однородной цепью Маркова, а вероятности pij - переходными вероятностям этой цепи. В этом обозначении первый индекс всегда будет определять, в каком состоянии находилась система в предшествующий момент времени, а второй индекс указывает, в какое состояние перейдет система в последующий момент времени. Пусть число состояний конечно и равно l. Тогда полная вероятностная картина возможных изменений, осуществляющихся при переходе от одного состояния к другому, задается матрицей
120
