3267

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1 y x y b / a,

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

3.84 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1910 11 12 13 14 15 16 17 18 19 > Следующая >>>

D c X

... c

c2D X

cov X

1 1

i 1

j 1

ci c j

ij .

i, j

Используя свойство неотрицательности дисперсии из формулы (3), положив в ней с1=t, с2=1, получим

D(tX+Y)=t2ζ11+2tζ12+ζ22≥0

при любом t R. Отсюда дискриминант

2
2		0 или				22 ,
12 11 22		0 или		12	11	22 ,
то есть

	cov X,Y		D X D Y .			(4)

Выше было отмечено, что для независимых СВ X и Y

сov(Х,Y)=0.

Следовательно, если cov(X,Y)≠0, то СВ X и Y зависимы. В качестве количественной характеристики степени

зависимости СВ X и Y вводится коэффициент корреляции.

Коэффициентом корреляции СВ X и Y называется число, определяемое формулой

	cov X,Y	.	(5)

x, y
	D X D Y


Для ρx,y справедливо утверждение:
Коэффициент корреляции удовлетворяет			неравенству

|ρx,y|≤1, причем если Y линейно выражается через X, то есть

Y=aX+b, где а и b -постоянные, то |ρx,y|=1 (ρx,y=±1).

Первая часть утверждения следует из неравенства (4). Докажем вторую его часть. Пусть Y=aX+b. Тогда

D(Y)=D(aХ+b)=D(аX)=а2D(X). cov(X,Y)=M[(X-M(X)(Y-M(Y))]=M[(X-M(X))(aX+b-

-M(aX+b))]=M[a(X-M(X))(X-M(X))]=aD(X).

Используя (5), получаем

	aD X	a

x, y x,ax b		a
x, y x,ax b	D X a2D X
	D X a2D X

xy 1 .

Имеет место и обратное утверждение: если коэффициент корреляции |ρx,y|=1, то между X и Y существует линейная связь.

Отметим, что из свойства 1 ковариации следует, что для независимых СВ X и Y ρx,y=0. Обратное утверждение неверно.

СВ X и Y, для которых ρx,y=0, называются

некоррелированными.

Из вышеизложенного следует, что независимые случайные величины некоррелированны, а некоррелированные случайные величины необязательно независимы.

Пример. Совместное распределение СB X и Y задано таблицей.

Найти М(Х), М(Y), D(Х), D(Y), cov(X,Y).

				Y					-1													0										1
				X					-1													0										1
				X
			-1						1/8										1/12												7/24
			1						5/24												1/6											1/8
M X				x			p		1	1	1				7		1	5 1 1								1		1				1	1	0;
M X				x			p		1								1									1						1		0;
				i			ij		8 12						24			24				6	8			2						2
		i			j				8 12						24			24				6	8			2						2
M Y					y			p	1			1				5		0				1 1				1			7 1
M Y					y	j		p	1									0								1
						j		ij				8			24				12				6			24						8
				j			i					8			24				12				6			24						8
1	1	1	5			1		;
1		1						;
3			12			12
		D X							x M X							2 p							1 2	1	1 2		1					1 ;
		D X							x M X							2 p							1 2		1 2							1 ;
									i								ij						2			2
							i	j															2			2
D(Y )							( y M (Y ))					2	p ( 1					1		)		2	1		(0	1				)	2	1
D(Y )							( y M (Y ))						p ( 1							)					(0					)
								i						ij				12					3			12						4
				i		j												12					3			12						4
															92

(1			1	)	2		5	169			1	1	1	121	5	1	169 4	3	121	5

		12				12		144			3	144	4	144	12 144			12
		12				12		144			3	144	4	144	12 144			12
	1 1284								107	;

144				12				144
144				12				144

cov X,Y										xi		M X			yi		M Y		pij
						i	j
		xi		M X							yi		M Y			pij
i									j
1			1		1		1			0		1		1			1	1	7

					12		8					12		12				12	24
					12		8					12		12				12	24
1		13		5		1		1		11		1		1		;

	12		24		12		6			12		8		4
	12		24		12		6			12		8		4
X,Y				cov X,Y								1/ 4						3	0, 29 .


				D X D Y								1 107 /144						107
				D X D Y								1 107 /144						107

10.4. Нормальный закон распределения двумерной СВ

Двумерная СВ (X,Y) распределена по нормальному закону, если совместная плотность распределения вероятностей имеет вид

f x, y

exp{

(

2 x

y 1

2 1

y my

2 xy

)}

(6)

Плотность распределения вероятностей для нормального закона зависит от пяти параметров. Чтобы выяснить их вероятностный смысл, найдем одномерные плотности и коэффициент корреляции СВ Х и Y. Для нахождения одномерной плотности распределения СВ Х воспользуемся равенством

(x m )2

(x mx )( y my )

( y my )2

(x m )2

(7)

(x m )2

( y my )

(x m )

(x m )2

)

x, y

x mx

(8)

2 1

y 1

x m

Аналогично получаем

Получили, что СВ Х и Y распределены каждая по нормальному закону. Тем самым выяснили смысл четырех параметров mx, my, ζx, ζy : mx и my – математические ожидания, ζx и ζy – средние квадратические отклонения СВ Х и Y.

Точку на плоскости с координатами (mx, my) называют

центром рассеивания.

Вычислим теперь коэффициент корреляции. Так как дисперсии СВ Х и Y найдены, то нужно вычислить ковариацию. Для этого воспользуемся формулой

cov X,Y

M X Y

M X

M Y ,

где

M X Y

xyf

x, y

dxdy

x 2

/(2 1

xy2

) ,

отсюда

x mx

M XY

y - my

x mx

y exp

dy dx.

σ y 2

Интеграл, стоящий в круглых скобках, можно рассматривать как МО СВ, распределенной по закону

N my xy y \ x x mx , y 1	2	,
	xy

поэтому он равен

my xy y \ x x mx .

M XY

my xe

x x mx e

mxmy

x x

2 x

mxmy

xy y x .

Для ковариации получаем

cov X,Y

mx my

y x mx my

y x

(9)

и для коэффициента корреляции

cov X,Y

(10)

D X D Y

то есть параметр

в нормальном законе двумерной СВ есть

коэффициент корреляции составляющих СВ Х и Y. Утверждение. Для СВ Х и Y, распределенных

нормально с плотностью (6), независимость равносильна некоррелированности.

Мы уже знаем, что из независимости любых СВ следует их некоррелированность. Покажем, что из некоррелированности нормально распределенных с плотностью (6) СВ следует их независимость. Действительно, если СВ Х и Y некоррелированы, то ρху=0, тогда

							2	y my	2
					1 x mx		2									2
					1 x mx									x	mx	2
		1			2	x		y			1			x	mx
		1									1			2	2

f x, y				e									e			(11)
															x
	2
												2
		x	y							x		2
		x	y							x

			y	my	2
			y	my
1		e	2	2		f x f y ,
		e		y		f x f y ,
				y

y	2
y

что означает независимость СВ Х и Y.

Отметим, что в этом случае оси координат ОХ и OY называются главными осями рассеивания.

10.5. Эллипс рассеивания

Эллипсом рассеивания двумерной нормально распределенной с плотностью (6) СВ называется эллипс, в каждой точке которого плотность имеет одно и то же постоянное значение. Эллипс, в точках которого плотность распределения вероятностей (6) постоянна и равна

					1								2
	f x, y		const		1					exp					,

													2
								2
						2 x y	1		2 1

								xy						xy
определяется уравнением
		2			x mx		y my				y my		2
	x m	2			x mx		y my				y my
	x		2												2 .
2			2	xy					2						2 .
2				xy					2
	x					x	y					y

С помощью преобразования поворота системы координат плотность нормального распределения (6) всегда может быть приведена к каноническому виду (11) с главным эллипсом рассеивания, описываемым уравнением

				2		y my	2
			x m	2		y my		2
			x					2
			2		2
			x			y
Если	x	y	, то рассеивание называется круговым.
	x	y

Пример. Двумерная СВ (Х,Y) подчиняется каноническому нормальному распределению с параметрами

тх=ту=0, ζх, ζу.

Вычислить вероятность попадания случайной точки (Х,Y) в область, ограниченную Dη (ограниченную главным

эллипсом рассеивания). Решить самостоятельно.

11.ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН

11.1.Закон распределения функции от одной СВ

Пусть (Ω, ,Р) - произвольное вероятностное

пространство и X=Х(ω) – некоторая СВ (ω Ω).

Функцией Y= (Х) СВ X называется суперпозиция действительной функции X=Х(ω), заданной на Ω, и функции

φ(х), заданной на действительной оси R, т.е. Y= [Х(ω)]=Y(ω).

Для дискретных вероятностных пространств функция Y(ω) является случайной величиной, так как никаких ограничений на функцию Y(ω) не налагается. Для произвольных вероятностных пространств требуется, чтобы

(Y<y)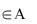 у.

Утверждение. Если X - дискретная СВ, имеющая закон распределения (хk, рk) k=1, 2,..., который можно записать в

виде табл.1,		и Y=		(Х), где		-неслучайная функция, то Y
также является дискретной CВ, причем ее возможные значения
уk= (хk).
					Таблица 1
	X		x1		x2	x3	…	xk	…
	P(X)		p1		p2	p3	…	pk	…

Если (х) – монотонная функция, то все значения yk

различны и P(Y=yk)=P(X=xk), то есть СВ Y имеет следующий закон распределения (табл.2)

Таблица 2

Y	(x1)	(x2)	…	(xk)	…
P(Y)	p1	p2	…	pk	…

Если при этом (х) – немонотонная функция, то среди ее значений у1,у2,у3,…,уk,… могут быть одинаковые. В этом

случае столбцы с равными значениями (хi) объединяются в

один столбец, а соответствующие вероятности складываются, т. е.

P Y

P X

xi .

i: xi yk

Утверждение. Если Х – непрерывная СВ с ФР F(x) и

плотностью

вероятности

f(x) и Y= (х),

причем

(х) –

монотонно

возрастающая

непрерывно

дифференцируемая

функция, а х=

-1(у) – обратная функция, то

F(y)=P(Y<y)=P( (х)<y)=P(X<

-1(х))=F[ -1(х)].

Дифференцируя последнее равенство по у, получаем

F y F -1

-1

или f y

-1

-1 y .

(x)

Y<y

X<x

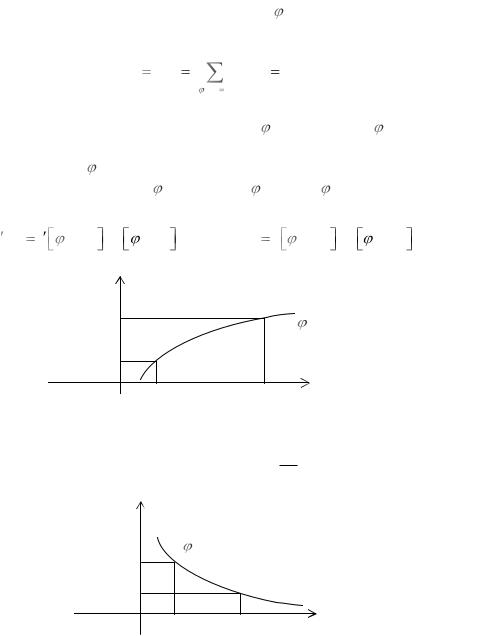
Если у=θ(х) - монотонно убывающая функция, то аналогично получаются следующие соотношения:

F(y)=1-F[θ-1(y)], f(y)= -f[θ-1(y)] dyd [θ-1(y)]. y

y= (x)

y
Y<y
0 X<x	x	x

Выражения для плотности вероятности СB Y и для монотонно возрастающей и для монотонно убывающей функции θ(х) можно объединить:

f y	f	1	y		d	1 y	.	(1)
		1
					dy
					dy
Пример. F(x)=1-e-x у=е-x, x>0. Найти F(у).
Предлагается решить самостоятельно.
Если (х) - немонотонная функция, то
	F y				f x dx ,			(2)
		k	k	y
где k(y) означает k-й интервал на оси ОХ, на котором								(х)<y.

Плотность f(y) затем получается дифференцированием F(y) по

у.

Отметим важный частный случай формулы (1) для непрерывной СВ. Пусть Y=аХ+b, где а и b - постоянные, причем а≠0. В данном случае

Отсюда

f y	1		f	y b	,	(3)
		a		a

и можно заключить, что график плотности распределения СВ Y получается из графика плотности распределения СВ X изменением масштаба и cдвигом вдоль одной из осей. Вид кривой при этом не меняется.

Семейство законов распределения, описываемых ФР F((x-b)/а), где F(х) - фиксированная ФР, b R, а>0, называется

видом распределения. При этом b называется параметром сдвига, а - масштабным множителем. Из этого определения для непрерывной СВ следует утверждение.

Семейство законов распределения, описываемых

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1910 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20223.75 Mб153258.pdf
#
15.11.20223.82 Mб33263.pdf
#
15.11.20223.82 Mб13264.pdf
#
15.11.20223.83 Mб13265.pdf
#
15.11.20223.83 Mб23266.pdf
#
15.11.20223.84 Mб23267.pdf
#
15.11.20223.85 Mб03268.pdf
#
15.11.20223.86 Mб03269.pdf
#
15.11.20223.86 Mб13270.pdf
#
15.11.20223.87 Mб03271.pdf
#
15.11.20223.88 Mб13272.pdf