
Начала математического анализа. Часть 1. Горбунов В.В., Соколова О.А
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
В.В. Горбунов О.А. Соколова
Начала математического анализа Часть 1
Учебное пособие
Воронеж 2003
УДК 517.2
Горбунов В.В., Соколова О.А. Начала математического анализа. Часть 1: Учебное пособие. Воронеж: Воронеж. гос. техн. ун-т, 2003. 105 с.
В учебном пособии излагаются элементы математического анализа. Теоретический материал иллюстрируется большим количеством примеров. Содержатся вопросы для самопроверки и задачи для самостоятельного решения.
Издание предназначено для студентов первого курса, обучающихся по специальности 120200 «Автоматизированное оборудование», изучающих дисциплину «Математика».
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе Microsoft Word и содержится в файле
“МатАн1.doc”.
Табл. 3. Ил. 23. Библиогр.: 3 назв.
Научный редактор: д-р физ.-мат. наук В.Д. Репников
Рецензенты: кафедра математики, информ. технологий и естественных дисциплин Воронежского
института экономики и права (зав. кафедрой к.т.н., доцент Павлов И.О.); д-р физ.мат.-наук В.А. Родин
Издается по решению редакционно-издательского совета Воронежского государственного технического университета.
 Гобунов В.В., Соколова О.А., 2003
Гобунов В.В., Соколова О.А., 2003
Оформление. Воронежский государственный технический универси-
тет, 2003
ВВЕДЕНИЕ
Изучение высшей математики студентами технических специальностей связано с необходимостью освоения математического аппарата, используемого в большинстве курсов по специальности.
Интенсивная компьютеризация образовательной, а в последующем, и профессиональной деятельности невозможна без твердых знаний разделов высшей математики, отсутствие которых сделает проблематичными попытки освоения новых областей знания, связанных с профессиональным ростом.
Данное пособие посвящено изучению следующих разделов высшей математики: начала математического анализа, дифференциальное исчисление функции одной переменной.
Пособие имеет следующую структуру. В начале каждого параграфа приводятся соответствующие теоретические сведения (определения основных понятий, уравнения, формулы, правила, признаки, методы). Затем следуют вопросы для самопроверки и примеры решения типовых задач различной степени трудности. Далее предлагаются задачи для самостоятельного решения. Ко всем задачам даны ответы.
Пособие рекомендовано студентам первого курса, обучающихся по специальности 120200 «Автоматизированное оборудование» в помощь к изучению курса высшей математики.
3

1.ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
1.1. Понятие множества и операции над множествами
Множеством называется совокупность объектов произвольной природы, объединенных по определенному признаку. Например, множество книг в библиотеке, множество определенным образом подобранных векторов, множество функций определенного вида. Множество считается заданным, если известны все элементы, из которых оно состоит, т.е. известен закон или правило, по которому можно определить все элементы множества. Множество может содержать конечное или бесконечное число элементов. Множества обозначаются заглавными буквами латинского алфавита, а входящие в них элементы – строчными буквами. Принадлежность элемента x множеству X обозначается символом ( x X ), если же элемент не принадлежит множеству, то используется символ .
Над множествами могут производиться операции сравнения. Множества A и B называются равными или эквивалентными, если они состоят из одинаковых элементов ( A B ). Если все элементы множества A содержатся во множестве B , то множество A являет-
ся подмножеством множества B ( A B ). Если ни один элемент |
|
множества |
A не содержится в B , то это обозначается следующим |
образом: A |
B . |
В математике используется понятие пустого множества, обо- |
|
значаемого символом . Это множество, в котором не содержится ни одного элемента, и потому оно является подмножеством любого множества.
Над множествами A и B может производиться операция сложения или объединения. Суммой, или объединением, множеств A и B называется совокупность элементов, входящих как во множество A , так и во множество B (обладающих либо свойством множества A , либо свойством множества B ). Сумма этих множеств
обозначается A B . Добавление пустого множества |
к любому |
множеству A не меняет этого множества, т.е. A |
A. |
Пересечением или произведением множеств A и |
B (или их |
общей частью) является совокупность элементов, входящих как во множество A , так и во множество B ; это множество обозначается
4

A B . Одновременное отсутствие элементов со свойствами множеств A и B означает, что пересечение этих множеств представляет собой пустое множество .
Разностью множеств A и B называется множество C , содержащее все элементы множества A , не содержащиеся во множестве B ; эта разность обозначается C A \ B .
При записи математических выражений целесообразно употреблять логическую символику. Вместо выражений «любое x из множества X » употребляют запись x X , где перевернутая латинская буква (квантор общности) взята от начала английского
слова Any |
– любой. Аналогично вместо выражений «существует |
элемент x |
из множества X » кратко пишут: x X , где переверну- |
тая латинская буква (квантор существования) является начальной
ванглийском слове Existence – существование.
Внастоящем пособии рассматривается множество действительных чисел, а также подмножества натуральных и рациональных чисел.
1.2. Понятие функции
Пусть X и Y – некоторые числовые множества. Если существует правило или закон, согласно которому каждому элементу x X поставлен в соответствие один элемент y Y , то говорят, что определена функциональная зависимость или однозначная функция y от x по закону y 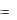 f x . При этом x называют незави-
f x . При этом x называют незави-
симой переменной (аргументом), y – зависимой переменной, множество X - областью определения функции, множество Y – областью значения функции.
Если же каждому элементу x X поставлены в соответствие
несколько элементов |
y Y , определена многозначная функция y |
от x . В дальнейшем, |
если нет специальных оговорок, будет рас- |
сматриваться множество однозначных функций.
5

1.3. Способы задания функций
Существует три основных способа задания функций: таблич-
ный, аналитический и графический.
Табличный способ. Этот способ широко используется при экспериментальных измерениях различных величин в науке и технике. В таблицах одну из переменных принимают за независимую переменную или аргумент (например, время), тогда другие величины будут функциями от этого аргумента. Табличный способ задания функциональной зависимости широко используется в различных базах данных.
Табличный способ задания функций позволяет производить интерполяцию при вычислении не содержащихся в таблице значений функции, соответствующие промежуточным значениям аргумента. По данным таблицы с помощью методов аппроксимации можно приближенно установить аналитический способ задания функции.
Аналитический способ. Этот способ состоит в формульном задании связи между аргументом и функцией. При аналитическом способе задания областью определения функции называется множество значений аргумента, при которых формула имеет смысл. Примером аналитически заданной функции является функция Римана
равная нулю, если x является иррациональным числом, и равная 1q ,
если x - рациональное число, выражающееся несократимой дробью со знаменателем q . Функция Римана определена на множестве дей-
ствительных чисел.
Ограничения, формирующие область определения несложных функции, связаны с выполнением указанных в формуле математических операций, и, как правило, сводятся либо к требованию неотрицательности подкоренного выражения для корней четной степени, либо к требованию неравенства нулю знаменателя , либо к условию положительности выражения под знаком логарифма, а также к некоторым другим.
Пример 1. Областью определения функции y |
4 |
x2 слу- |
жит отрезок 2,2 , областью значений функции - отрезок |
0,2 . |
|
6
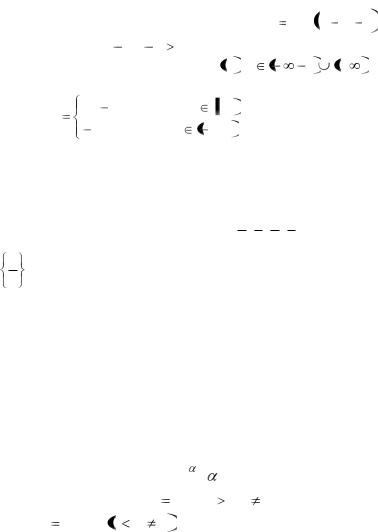
Пример 2. Область определения функции y |
log 5 x2 |
5x 6 |
||||||
определяется условием x2 |
5x |
6 |
0 . Решение неравенства позво- |
|||||
ляет найти область определения функции D y : x |
, 1 |
6, . |
||||||
Область определения функции часто задается вместе с функ- |
||||||||
цией. Например, y |
x 2 |
2x, |
если |
x |
0,8 |
. |
|
|
x 4 , если |
x |
6,0 |
|
|
||||
|
|
|
|
|||||
Существуют функции определенные на множестве натуральных чисел. Такие функции называются числовыми последовательностями. Числовые последовательности задаются формулой общего члена последовательности, записанного в фигурных скобках. На-
пример, гармоническая последовательность 1, 12 , 13 , 14 , 15 ,... обознача-
ется так: 1n .
Графический способ. При графическом способе задания функции связь между аргументом и функцией задается посредством графика. Графиком называется множество точек координатной плоскости, абсциссами которых являются значения аргумента, а ординатами – соответствующие значения функции.
1.4. Классификация функций
Основными элементарными функциями являются постоянная
функция y=const, |
степенная функция x |
( |
- любое действительное |
||
число), показательная функция |
y |
a x |
(a |
0, a 1) , логарифмиче- |
|
ская функция y |
loga x 0 a |
1 , |
тригонометрические функции |
||
sin x, cos x, tgx, |
ctgx и обратные |
тригонометрические функции |
|||
arcsin x, arccosx, arctgx, arcctgx.
Элементарные функции, не являющиеся простейшими, могут быть получены при помощи конечного числа алгебраических (сложение, вычитание, умножение, деление, возведение в степень с целым показателем, извлечение корня) и трансцендентных (возведение в степень с иррациональным показателем, логарифмирование, вы-
7

числение значений тригонометрических и обратных тригонометрических функций) операций. Алгебраическими называются элементарные функции, полученные с помощью конечного числа алгебраических операций. Алгебраические функции подразделяются на рациональные и иррациональные функции. К рациональным функциям относятся целая и дробная рациональные функции. Функция вида
P x a |
0 |
xn |
a xn 1 |
a |
2 |
xn 2 |
a |
n 1 |
x a |
n |
, |
|
|
1 |
|
|
|
|
|
||||
где n - натуральное число или ноль, a0 , a1 , a2 , , an |
- любые дей- |
||||||||||
ствительные числа (коэффициенты), называется целой рациональной функцией, или алгебраическим многочленом степени n. Многочлен первой степени называется линейной функцией . Отношение двух целых рациональных функций
|
a |
0 |
xn |
a xn 1 |
a |
n 1 |
x a |
n |
R x |
|
|
1 |
|
|
|||
b xm |
b xm 1 |
b |
|
x b |
||||
|
|
|||||||
|
0 |
|
1 |
m 1 |
|
m |
||
называется дробно – рациональной функцией. Алгебраическая функция, не являющаяся рациональной, называется иррациональной
функцией, например, функция f x

 x 2 x3/ 5 является ирра-
x 2 x3/ 5 является ирра-
циональной.
Алгебраические функции, не являющиеся рациональными или иррациональными, называются трансцендентными функциями, на-
пример, функции f x cos3x e x и x
cos3x e x и x 32x ctgx являются
32x ctgx являются
трансцендентными.
Сложной функции или композицией функций (функция от функции) называется такая зависимость у от х, что у является функ-
цией от переменной u , а u |
в свою очередь зависит от переменной |
||
x . Пусть y F u и u |
x . Тогда функция y F x является |
||
|
|
|
|
сложной функцией. Функция вида y |
ln x представляет собой |
||
пример сложной функции, где в качестве промежуточной функции
выступает |
u |
ln x . |
Существуют сложные функции, |
содержащие |
||||||||
несколько |
промежуточных |
функций, |
например, |
в |
функции |
|||||||
|
|
|
|
|
y |
зависит |
от |
первой |
промежуточной |
функции |
||
y |
sin |
log 4 x |
||||||||||
|
|
|
|
|
|
|
|
|||||
u |
|
v , |
а |
v |
является второй |
промежуточной функцией x , т.е. |
||||||
v |
log4 x . |
|
|
|
|
|
|
|
|
|||
8
