
3115
.pdf
Из рис.12 становится понятным геометрический смысл дифференциала dy , представляющего приращение ординаты касатель-
ной при переходе от точки a к точке a  x .
x .
Для выяснения физического смысла производной рассмотрим движение материальной точки по оси Oy . Координата материаль-
ной точки |
|
y является дифференцируемой функцией времени t . В |
||||||||||||
момент времени t0 |
материальная точка имеет координату y t0 . В |
|||||||||||||
момент времени t0 |
|
|
t материальная точка приобрела координату |
|||||||||||
y t0 |
t . |
Посчитаем среднюю скорость перемещения материаль- |
||||||||||||
ной точки за промежуток времени |
t |
|
|
|
||||||||||
|
|
|
|
|
|
Vср |
|
y t0 |
t |
y t |
|
y |
. |
|
|
|
|
|
|
|
|
|
t |
|
|
t |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если устремить |
t к нулю и рассмотреть lim Vср , равный |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 0 |
мгновенной скорости материальной точки Vмгн , то можно заметить, |
||||||||||||||
что lim |
|
V |
|
= lim |
|
y |
= |
dy |
, т.е. предел отношения приращения ко- |
|||||
t |
0 |
ср |
t 0 |
t |
dt |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
ординаты материальной точки к приращению времени и есть с одной стороны производная координаты по времени, а с другой стороны - мгновенная скорость материальной точки.
Связь непрерывности и дифференцируемости функции устанавливается следующей теоремой.
Теорема. Если функция y f x дифференцируема в некоторой точке x0 , то она непрерывна в этой точке.
Доказательство. Функция дифференцируема в точке, следова-
тельно, существует lim |
|
|
y |
f (x0 ) . По основной теореме о беско- |
||||||
|
|
|
||||||||
|
|
x |
||||||||
|
|
|
|
x |
0 |
|
|
|
|
|
нечно малых величинах |
|
|
|
|
||||||
|
|
y |
|
f (x0 ) |
x |
или y |
f (x0 ) x |
x x , |
||
|
|
|
|
|||||||
|
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
где |
|
x |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
y |
|
0 при |
x 0 , поэтому функция непре- |
|||||
рывна.
39
Обратное утверждение неверно. Из того, что функция непрерывна в точке, не следует, что она дифференцируема, т.е. непрерывная функция может не иметь производную в этой точке.
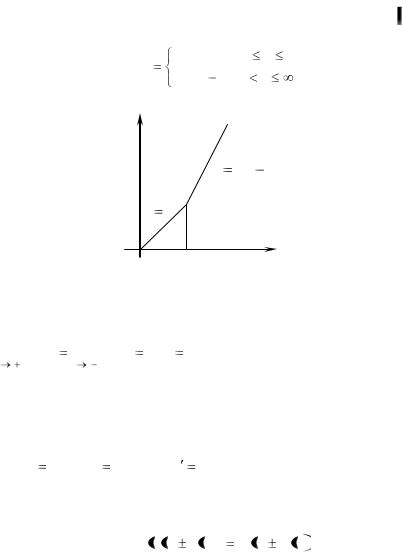
Пример 3.1. Функция f(x) определена на промежутке 0, 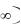 следующим образом (рис.13):
следующим образом (рис.13):
|
|
f (x) |
x, |
0 |
x |
1, |
|
|
|
|
|
2x 1, |
1 |
x |
. |
|
|
||
|
|
|
|
|
|
||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
y |
2x |
1 |
|
|
|
|
|
|
y x |
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
x |
|
|
|
|
|
|
Рис. 13. |
|
|
|
|
|
При |
x=1 |
функция |
непрерывна, |
так |
как |
||||
lim f (x) |
lim |
f (x) |
|
f (1) 1 , но не дифференцируема. |
|
||||
x 1 0 |
x 1 0 |
|
|
|
|
|
|
|
|
|
|
3.2. Правила дифференцирования |
|
|
|||||
Теорема 1. Производная постоянной величины равна 0, т.е. |
|||||||||
если y c , где c |
const, то y 0 . |
|
|
|
|
|
|||
Теорема 2. Производная суммы (разности) дифференцируемых функций равна сумме (разности) производных этих функций, т.е.
u x v x
v x u
u x
x v
v x .
x .
Доказательство. По определению производной и основным теоремам о пределах получаем:
40
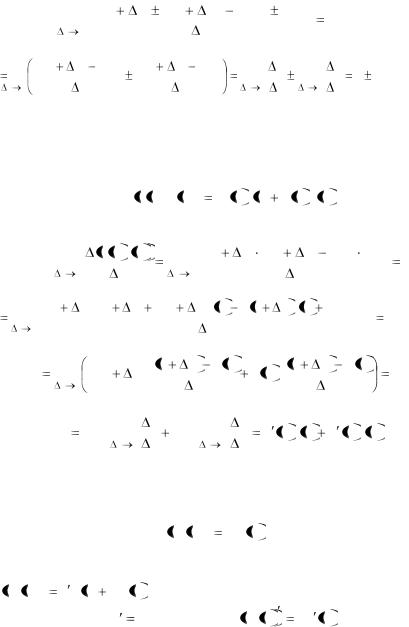
|
y'= lim |
(u(x |
|
x) |
v(x |
x)) |
(u(x) |
v(x)) |
|
|
||||
|
|
|
|
x |
|
|
|
|
|
|
||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
||
lim |
u(x |
x) |
u(x) |
|
v(x |
x) |
v(x) |
lim |
u |
lim |
u |
u' v'. |
||
|
x |
|
|
|
x |
|
|
v |
v |
|||||
x 0 |
|
|
|
|
|
x 0 |
x 0 |
|
||||||
Теорема 3. Производная произведения двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение производной второй функции на первую, т.е.
u x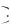 v x
v x u
u x v x
x v x u x v
u x v x .
x .
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
lim |
|
u x v x |
|
|
|
lim |
|
u(x |
x) |
v(x |
x) |
u(x) v(x) |
|||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||
|
|
x |
0 |
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
lim |
|
v(x |
x)u(x |
x) |
|
u(x |
x)v x |
u x |
|
|
x v x |
u(x)v(x) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
u(x |
x) |
v x |
|
x |
v x |
|
v x |
u x |
x |
u x |
|||||||||
|
|
|
|
|
|
v |
|
|
|
x |
|
|
|
||||||||||
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
u(x) lim |
|
v |
v(x) lim |
|
u |
v x u x |
u |
x v x . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x |
|
x |
|||||||||||||||||
|
|
|
|
|
x 0 |
|
|
x |
0 |
|
|
|
|
|
|
|
|
||||||
Теорема 4. Постоянный множитель можно выносить за знак производной, т.е.
cu x cu
cu x .
x .
Доказательство. По теореме о производной произведения cu x c u x
c u x cu
cu x . Поскольку производная постоянной вели-
x . Поскольку производная постоянной вели-
чины равна нулю c 0 , то получаем cu x |
cu x . |
41 |
|
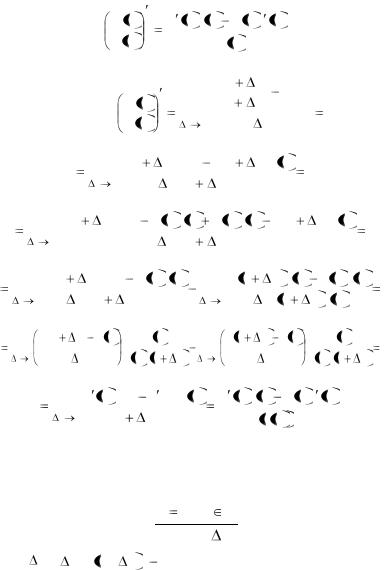
Теорема 5. Производная частного двух дифференцируемых функций равна дроби, у которой знаменатель равен квадрату знаменателя, а числитель есть разность произведений производной числителя на знаменатель и производной знаменателя на числитель, т.е.
|
|
|
|
|
|
|
|
u x |
|
|
|
u x v x u x v x |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
v x |
|
|
|
|
|
|
|
|
v2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x |
x) |
|
|
u(x) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Доказательство. |
|
|
|
|
u x |
|
lim |
|
|
|
v(x |
x) |
|
|
v(x) |
|
|||||||||||||||||||||||
|
|
|
|
v x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
lim |
|
|
u(x |
|
|
x)v(x) |
|
|
|
v(x |
x)u x |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xv(x |
|
|
|
x)v(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
lim |
u(x |
x)v(x) |
|
u x v x |
|
|
|
u x v x |
v(x |
|
|
x)u x |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xv(x |
|
|
|
x)v(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lim |
u(x |
|
x)v(x) u x v x |
|
lim |
|
v x |
|
|
x u x |
|
|
v x u x |
|
|||||||||||||||||||||||||
|
xv(x |
|
|
|
x)v(x) |
|
|
|
|
|
|
xv x |
x v x |
|
|||||||||||||||||||||||||
x 0 |
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|||||||||||||||||||||||||||
lim |
|
u(x |
x) u x |
|
|
|
|
|
|
v x |
|
|
|
|
lim |
v x |
x v x |
|
|
u x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
|
v x v x |
|
x |
|
|
x |
|
|
|
|
|
v x v x x |
|
||||||||||||||||||
x 0 |
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
lim |
|
u |
x v(x) |
v (x)u x |
|
|
|
|
u |
|
x v x |
|
|
u x v x |
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x 0 |
v(x |
x)v(x) |
|
|
|
|
|
|
|
v x 2 |
|
|
|
|
|
|
|||||||||||||||||||
3.3.Производная степенной, показательной
итригонометрических функций
1.Степенная функция y xn , n R .
Найдем приращение функции y , придав аргументу x при-
ращение x : y  x
x 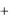 x n xn . Поэтому в соответствии с определением производной имеем:
x n xn . Поэтому в соответствии с определением производной имеем:
42
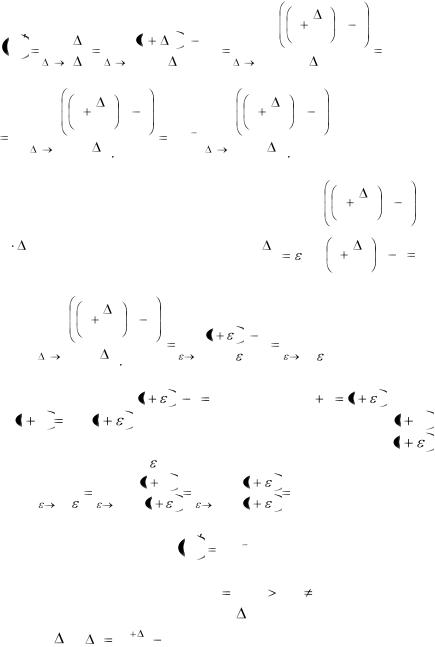
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x n |
1 |
|
x |
n |
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x n |
|
|
|
|
|
|
y |
|
|
|
|
|
x |
|
x |
n |
x |
n |
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
lim |
|
|
lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x |
0 |
|
|
x |
|
0 |
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x n |
|
|
|
|
|
x |
|
|
|
|
|
nxn 1 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Покажем, что бесконечно малые величины |
1 |
|
|
x |
n |
1 |
и |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n x |
являются эквивалентными. Пусть |
|
|
|
|
|
|
x |
|
, |
а 1 |
|
|
x |
|
n |
1 |
z , |
|||||||||||||||||||||||||||||||
|
x |
|
|
|
|
x |
|
|
x |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
n |
1 |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
lim |
|
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
0 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
0 n |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Поскольку |
|
|
|
|
1 |
|
n |
1 |
|
z , |
|
|
то |
z |
1 |
|
1 |
|
|
n , |
|
а |
||||||||||||||||||||||||||
ln 1 |
z |
|
n ln 1 |
|
|
|
|
. Так как бесконечно малая величина |
ln 1 |
z |
||||||||||||||||||||||||||||||||||||||||
эквивалентна величине |
z , а бесконечно малая величина |
ln 1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
эквивалентна величине |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
lim |
|
|
z |
|
|
|
lim |
|
ln 1 |
|
z |
lim |
n ln 1 |
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
0 n |
|
|
|
|
|
|
|
0 n ln 1 |
|
|
|
|
0 n ln 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Таким образом, производная степенной функции равна |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x n |
|
|
nx n 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2. Показательная функция y |
a x , a |
|
|
|
|
0, a |
1. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Найдем приращение функции |
|
y , |
придав аргументу x |
при- |
||||||||||||||||||||||||||||||||||||||||||||
ращение |
|
x : |
|
|
y |
|
|
a x x |
|
a x . Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
43

|
|
y |
|
a x x a x |
|
a x 1 |
|||
a x |
lim |
|
lim |
|
a x |
lim |
|
|
|
|
|
|
|
|
|||||
|
x 0 |
x |
x 0 |
x |
x 0 |
|
x |
||
В пределе перейдем к новой переменной y |
a x |
1, которая |
|||||||
тоже является бесконечно малой величиной. Используя второй за-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
мечательный предел lim 1 |
y |
|
|
|
e и соотношение |
x |
log a 1 |
y , |
|||||||||||||||||||||||||||||||||
y |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a x |
lim |
|
a x |
1 |
a x lim |
|
|
|
|
|
y |
|
|
|
|
a x lim |
|
|
1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||
|
x 0 |
|
|
|
|
|
x |
|
|
y |
0 log a 1 |
|
y |
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
log a 1 |
y |
y |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a x lim |
|
|
1 |
|
|
a x ln a . |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0 log a e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким образом, производная показательной функции равна |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a x |
|
== ax ln a . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
При a = e имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e x |
|
|
e x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Тригонометрические функции y |
|
sin x, y |
|
cos x, |
y |
tgx, |
|||||||||||||||||||||||||||||||||||
y ctgx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для функции y |
|
sin x имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin |
|
|
x |
|
cos x |
|
x |
|
|
|
|
|
|
||||||
sin x |
lim |
|
|
sin |
|
x |
x |
|
sin x |
lim |
2 |
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
sin |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 lim |
|
|
2 |
|
|
cos x |
|
|
|
|
cos x |
lim |
|
2 |
|
|
cos x , |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x |
|
2 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
44

|
Для функции y |
cos x имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
x |
|
x |
sin |
|
|
x |
|
|
|
|||||||
cos x |
|
|
lim |
cos x |
x |
cos x |
2 lim |
2 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
sin |
x |
|
x |
|
sin |
x |
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||
- 2 |
lim |
2 |
|
2 |
|
|
|
- sin x lim |
2 |
|
|
|
|
|
|
- sin x , |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
- sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Для нахождения производных функций |
y |
tgx, |
|
|
y |
ctgx вос- |
||||||||||||||||||||||||||||||||||||
пользуемся формулой производной частного: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
tgx |
|
sin x |
|
|
|
sin x |
cos x |
sin x cos x |
|
|
cos x 2 |
sin x 2 |
|
|
1 |
|
|
|
. |
||||||||||||||||||||||||
|
cos x |
|
|
|
|
|
cos x 2 |
|
|
|
|
|
|
|
|
|
|
cos x 2 |
|
|
|
|
|
cos2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgx |
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ctgx |
|
|
cos x |
|
|
|
cos x |
sin x |
cos x sin x |
|
|
|
|
|
sin x 2 |
cos x 2 |
|
|
1 |
|
. |
||||||||||||||||||||||
|
|
sin x |
|
|
|
|
|
sin x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
sin 2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctgx |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3.4. Обратные функции. Производная обратной функции |
||||||||||||||||||||||||||||||||||||||||||
|
Пусть задана функция y |
f x |
|
с областью определения D и |
|||||||||||||||||||||||||||||||||||||||
множеством значений E . Если каждому значению y |
|
|
E ставится в |
||||||||||||||||||||||||||||||||||||||||
соответствие единственное значение |
x D , то определена функция |
||||||||||||||||||||||||||||||||||||||||||
x |
y с областью определения E и областью значений D , назы- |
||||||||||||||||||||||||||||||||||||||||||
ваемая обратной по отношению к функции y |
|
|
f |
x . Про функции |
|||||||||||||||||||||||||||||||||||||||
45

y f x и x
и x 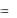 y
y говорят, что они взаимно обратные. Если возможно решить уравнение y
говорят, что они взаимно обратные. Если возможно решить уравнение y 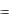 f x
f x относительно x , то по исходной функции можно найти обратную функцию. Например, для функции
относительно x , то по исходной функции можно найти обратную функцию. Например, для функции
y |
3x |
обратной функцией будет функция |
x |
|
1 |
. Однако, |
если, |
|||
|
|
|||||||||
|
|
|
|
|
|
|
3y |
|
|
|
как обычно, независимую переменную обозначить через |
x , а зави- |
|||||||||
симую |
переменную через |
y , |
то функция, |
обратная |
функции |
|||||
y |
f x |
, запишется в виде |
y |
x . В последнем примере для |
||||||
функции y 3x обратной будет функция y |
1 |
. |
|
|
|
|
||||
3x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Для существования взаимно однозначного соответствия |
меж- |
||||||||
ду множествами E и D необходима монотонность функции. Если функция возрастает (убывает), то и обратная функция тоже возрастает (убывает). Следует отметить, что если графики взаимно обрат-
ных функций |
y |
f |
x |
|
и x |
y |
совпадают, то графики функций |
|||||||||||||||||
y f x |
и y |
|
x симметричны относительно биссектрисы угла |
|||||||||||||||||||||
первой четверти. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема. Если функция |
y |
f x |
|
строго монотонна на про- |
||||||||||||||||||||
межутке |
a,b |
и имеет неравную нулю производную |
|
f |
x |
в любой |
||||||||||||||||||
точке этого промежутка, то обратная ей функция |
x |
|
y |
также |
||||||||||||||||||||
имеет производную |
|
y |
в соответствующей точке, |
определяемую |
||||||||||||||||||||
равенством |
x |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
f |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Доказательство. |
Рассмотрим |
обратную |
функцию |
x |
y . |
|||||||||||||||||||
Пусть аргумент y |
и функция x |
испытывают приращения |
y |
и x . |
||||||||||||||||||||
Поэтому можно записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
|
|
lim |
x |
lim |
1 |
1 |
|
|
|
|
|
1 |
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
y |
|
y |
|
|
|
|
y |
|
|
f |
x |
|
||||||||
|
|
|
|
|
y |
0 |
y 0 |
|
|
|
lim |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||
Таким образом, производная обратной функции равна обратной величине производной исходной функции.
Используем теорему о дифференцировании обратной функции для нахождения производной логарифмической функции y log a x .
46

Рассмотрим функцию |
|
y a x с известной |
производной |
||||
a x |
a x ln a . Тогда для обратной функции x log a y можно ука- |
||||||
зать производную x |
|
1 |
1 |
. Поменяв a x на |
y , затем, пе- |
||
|
|
|
|
||||
|
y |
|
a x ln a |
||||
|
|
|
|
|
|
||
рейдя к привычным обозначениям для аргумента и функции, получим:
log a x |
1 |
. |
|
|
|||
x ln a |
|||
|
|
В частном случае для натурального логарифма имеем:
|
|
|
|
|
|
|
|
|
|
ln x |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Аналогичным образом могут быть получены производные об- |
||||||||||||||||||||||||||||||||
ратных |
тригонометрических |
|
функций. |
Например, |
|
для |
функции |
||||||||||||||||||||||||||
y |
arcsin x обратной функцией является функция x |
|
sin y . Тогда |
||||||||||||||||||||||||||||||
|
|
arcsin x |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
cos y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
sin y |
|
|
|
|
|
1 |
sin |
2 |
y |
1 |
x |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Подобным образом получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
arccos x |
|
|
|
1 |
|
, |
arctgx |
|
|
|
1 |
, |
arcctgx |
|
|
|
|
1 |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
x2 |
||||||||||||||||
|
|
1 |
x 2 |
1 |
|
|
1 |
|
|
||||||||||||||||||||||||
|
|
3.5. Сложные функции. Производные сложных функций |
|||||||||||||||||||||||||||||||
|
Пусть y f u |
|
и |
u |
|
|
x , |
тогда |
|
|
|
y |
f u x |
является слож- |
|||||||||||||||||||
ной функцией с промежуточным аргументом u |
|
и независимым ар- |
|||||||||||||||||||||||||||||||
гументом x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Теорема. Если функция u |
|
x |
|
|
|
имеет производную ux в |
||||||||||||||||||||||||||
точке |
x , а функция |
y |
f |
u |
имеет |
|
|
производную yu |
|
в |
точке |
||||||||||||||||||||||
u |
x , то сложная функция |
|
y |
f u x |
|
имеет производную |
y x в |
||||||||||||||||||||||||||
точке x , находящуюся по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
yx yu ux .
47

|
|
|
|
Доказательство. |
|
Поскольку |
|
|
lim |
|
y |
yu , |
то |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 u |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
||||
|
y |
|
|
yu u |
u , |
где |
|
u |
0 |
|
|
при |
|
u |
0 , причем |
||||
|
|
u |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Для функции |
u |
x , имеющей производную в точке |
x , |
||||||||||||
можно записать |
u |
ux |
x |
x , где |
|
|
x |
0 . |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
x |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Подставив значение |
|
u в выражение для |
y имеем |
|
|||||||||||
|
|
|
|
|
|
y yu ux x |
x |
|
|
u ux x |
|
|
x |
|
|||||
|
|
|
|
|
|
yuux x yu |
x ux |
|
|
u x |
|
u |
x . |
|
|||||
|
|
|
|
Рассмотрим предел |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
lim |
|
yu ux x yu |
x ux |
|
u x |
|
u |
x |
|
yu ux . |
|
|||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, производная сложной функции равна
yx yu ux .
3.6.Гиперболические функции и их производные
Вмеханике встречаются гиперболические функции, определяемые следующими формулами: гиперболический синус
|
ex |
e |
x |
|
shx |
|
|
|
, |
|
2 |
|
||
|
|
|
|
|
гиперболический косинус (цепная линия)
|
e x |
e |
x |
|
chx |
|
|
|
, |
|
2 |
|
||
|
|
|
|
|
гиперболический тангенс |
|
|
|
|
|
|
thx |
shx |
|
e x |
e |
x |
, |
chx |
|
e x |
e |
x |
48
