Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3115

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

3.04 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Теорема. (Необходимое условие возрастания (убывания)

функции). Если непрерывная и дифференцируемая на интервале a,b функция f x возрастает (убывает), то для любой точки этого

интервала

0 f

0 .

Доказательство: Пусть функция

x возрастает на интервале

a,b . Выберем произвольную точку х на интервале

a,b и

расмотрим отношение

f (x

f (x)

Поскольку функция

x возрастает, то, при

x >0 и

x > x

x > f

. Если

0 и x

x , то

f x

. В обоих случаях

f (x

f (x)

так как числитель и знаменатель дроби имеют одинаковые знаки. По

условию теоремы функция				f x		дифференцируема, следовательно,
имеет производную в точке				x , которая является пределом отноше-
ния
			f (x		x)	f (x)	0,

					x
					x
следовательно
f	(x)		lim		f (x	x) f (x)		0.

						x
			x	0		x
По аналогии	рассматривается случай, когда функция f x
убывает на интервале		a,b .

Геометрический смысл теоремы состоит в том, что для возрастающей дифференцируемой функции касательная к графику имеет положительный угловой коэффициент и образует острые положительные углы с положительным направлением оси Ох. Для убывающей дифференцируемой функции касательная к графику функции в любой точке имеет отрицательный угловой коэффициент.

Теорема. (Достаточное условие возрастания (убывания)

функции). Если функция f x непрерывна и дифференцируема на

интервале		a,b	и f x 0 ( f x 0)	для	любого	x	a,b , то
функция	f	x	является возрастающей (убывающей) на интервале
a,b .
Доказательство.
Пусть		f	x 0. Возьмем точки x1	и x2	из интервала		a,b , та-
кие, что	x1 < x2 . По теореме Лагранжа внутри отрезка					x1, x2 най-

дется такая внутренняя точка , что будет выполняться равенство

f x2

f x1

x1 .

Так

как

0 ,

x1 < x2 ,

то f

0 или

f x1

, т.е. функция

x на интервале

a,b возрастает.

По аналогии доказывается случай убывания функции.

Пример 5.1. Исследовать функцию

5 на воз-

растание и убывание.

Решение:

Производная

функции

равна:

3x2

3 3 x2

1 3 x

1 x

1 .

Методом интервалов легко

показать, что при x

0 , т.е. функция возрас-

тает. При x

1,1

0 , т.е. функция убывает.

5.2. Максимум и минимум функции

Точка x0 называется точкой максимума (точкой минимума)

функции y f x , если существует такая -окрестность точки x0 ,

что для всех остальных значений x из этой окрестности будет выполняться неравенство

f x0

f x , ( f x0

f x ) .

Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом функции.

Понятие экстремума функции является локальным для функции, поскольку всегда связано с определенной окрестностью точки из области определения функции. Необходимо отметить, что точки

экстремумов могут быть только внутренними точками области определения. Рассмотрим необходимое условие существования экстремума функции.

Теорема. (Необходимое условие экстремума). Если диффе-

ренцируемая функция

имеет в точке x

максимум или

минимум, то ее производная обращается в нуль в этой точке, т.е

0 .

Доказательство. Рассмотрим случай,

когда точка x0 является

точкой максимума. Это означает,

что в окрестности точки x0 вы-

полняется неравенство

или

x . Но тогда

f (x0

f (x0 )

если

x 0 , и

если

. Так как производная

(x0 )

lim

f (x0

f (x0 )

по условию теоремы существует, а

lim

0 ,

lim

0 ,

x 0 0

0 0

то получаем, что

0 .

Геометрический смысл теоремы состоит в том, что в точке

экстремума дифференцируемой функции

y f

касательная к еѐ

графику параллельна оси Ox .

Точки, в которых производная обращается в нуль называются

стационарными.

Однако, можно привести ряд примеров, когда обращение в нуль производной не связано с наличием экстремума. Например, для

функции y x3 еѐ производная y	3x2 равна нулю при x 0 , но в
начале координат функция y x3	не имеет экстремума.

Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция y 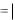x в точке x 0

производной не имеет, но точка x 0 является точкой минимума. Можно утверждать, что непрерывная функция имеет экстремум или

в точках, где производная функции равна нулю, или не существует.

Подобные точки называются критическими точками первого рода.

Теорема. (Достаточное условие экстремума). Если непре-

рывная функция y f x дифференцируема в некоторой 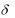- окрестности критической точки x0 и при переходе через нее слева направо производная f x меняет знак с плюса на минус, то x0 есть точка максимума; если же изменение знака происходит с минуса на плюс, то x0 является точкой минимума.


Доказательство.	Предположим, что производная f				x при пе-
реходе через точку x0	слева направо меняет знак с плюса на минус.
Тогда функция y f	x	возрастает на промежутке		x0	, x0	и
убывает на промежутке		x0 , x0	. Отсюда следует, что значение
f x в точке x0 является наибольшим на интервале				x0	, x0	,

что соответствует определению максимума функции в точке x0 . Аналогичным образом можно рассмотреть случай изменения

знака производной с минуса на плюс при переходе через точку x0 .

Пример 5.2. Найти экстремум функции у =

3 x2 .

Решение: Областью определения

функции

является вся

числовая ось. Находим производную y

3 x

3 3 x

3 3

Производная непрерывной функции не существует при x1 0

и равна нулю при x2	8 . Две критические точки разбивают всю об-
ласть определения функции на три интервала		,0 , 0,8 , 8, .
Определим знаки производной на каждом из трех интервалов.
	-
0	8

Рис. 16.

Следовательно, x1 0 является точкой максимума,	причем,
ymax 0 , а x2 8 является точкой минимума, ymin y 8		4	.
	3

В некоторых задачах удобнее использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.

Теорема. (Второй достаточный признак существования

экстремума). Если в

точке

первая

производная

функции

f x

равна нулю, а вторая производная в точке x0

существует и

отлична от нуля

0 , то при f

<0 в точке x0

функция

имеет максимум, а при

x0 > 0 функция имеет минимум.

Доказательство. Пусть для определенности

> 0 .

Так

как

(x0 ) lim

f (x0

f (x0 )

lim

f (x0

то

f (x0

окрестности

точки

x0 .

Если

x <0,

то f

x <0; если

x >0, то

x >0. При переходе через

точку x0 первая производная меняет знак с минуса на плюс.

По

предыдущей теореме x0

есть точка минимума.

Аналогично доказывается,

что если f

x0 < 0, то в точке

функция имеет максимум.

5.3. Наибольшее и наименьшее значение функции на отрезке

Рассмотрим функцию y f x , непрерывную на отрезке a,b . По известной теореме такая функция достигает своих наибольшего и

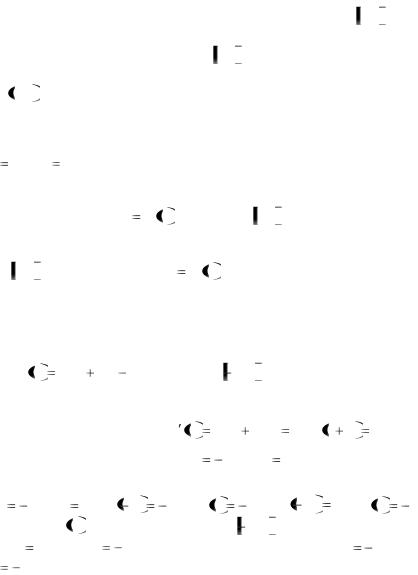
наименьшего значений. Эти значения функция может принять либо в точках экстремумов, либо на граничных точках отрезка a,b .

Получаем следующее правило нахождения наибольшего и наименьшего значений функции на a,b :

1)найти критические точки первого рода функции на интервале a,b ;

2)вычислить значения функции в найденных критических

точках;

3)вычислить значения функции на концах отрезка в точках

xa и x b ;

4)среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

Если функция y f x на отрезке a,b не имеет критических

точек, то в этом случае функция является монотонной, и свое наибольшее и наименьшее значения принимает на разных концах отрезка a,b . Если же функция y f x имеет лишь одну критическую

точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.

Пример 5.3. Найти наибольшее и наименьшее значение функ-

ций

3x4

10 на отрезке

4,2 .

Решение. Находим критические точки данной функции при-

равняв производную нулю: f

3x3

3x2

0 . Кри-

x 2

тическими точками оказались

2 и

0 . Находим значения

функции

критических

точках x1 , x2 и

на

границах отрезка

4 , x4

2 : f

11,

f 0

10 ,

4 6 ,

f 2

Функция

приняла

на отрезке

4,2

наибольшее

значение

fнаиб

при

4 и

наименьшее

значение

fнаим

при

2 .

5.4. Выпуклость и вогнутость графика функции. Точки перегиба

График дифференцируемой функции y f x называется выпуклым на интервале a,b , если любая касательная на этом интервале будет располагаться выше графика функции. График функции y f x называется вогнутым на интервале a,b , если любая ка-

сательная на этом интервале будет располагаться ниже графика функции.

Точки графика непрерывной функции y 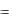f x , отделяющие

участки вогнутости и выпуклости графика, называется точками пе-

региба.

Интервалы выпуклости и вогнутости находят с помощью тео-

ремы.

Теорема. Если функция y f x в любой точке интервала a,b имеет отрицательную вторую производную, т.е. f x 0 , то график функции в этом интервале является выпуклым. Если же вторая производная положительная в любой точке интервала a,b , то

график функции является вогнутым на этом интервале.

Доказательство. Предположим, что на	интервале	a,b
f x 0 . Возьмем на графике функции произвольную точку		S с
абсциссой x0 a,b и проведем через точку S	касательную. Дока-

жем, что график функции расположен ниже этой касательной. Срав-

ним в точке	x	a,b	ординату кривой		y	f x	и ординату каса-
тельной yкас	x . Воспользуемся уравнением касательной
		yкас f (x0 )		f (x0 )(x		x0 ).
Тогда
	y	yкас	f (x) f (x0 ) f		(x0 )(x		x0 ).
По теореме о конечных приращениях
		f (x) f (x0 )		f (c)(x x0 ),
где c лежит между x и x0 .
				85

Поэтому

yкас

f (c)(x

x0 )

f (x0 )(x

x0 )

x0 .

Выражение

преобразуем по формуле Лагранжа:

f (c)

f (x0 )

f (c1 )(c x0 ),

где

точка

является некоторой

внутренней точкой

промежутка

x0 , c

. В результате получаем:

yкас

f (c1)(c

x0 )(x

x0 ).

Легко заметить, что если

x x0 , то

и c

0 . Если же

x0 , то

0 .

В любом случае произведение

(c x0 )(x

x0 ) 0 .

Поскольку

0 ,

то

yкас

0 ,

поэтому

во всех точках интервала

a,b ордината касательной больше орди-

наты графика, т.е. график функции является выпуклым. По аналогии

доказывается, что при

f x

график функции является вогну-

тым.

Для нахождения точек перегиба графика функции

f x

используется следующая теорема.

Теорема. Если в точке

вторая производная

непре-

рывной функции

x равна нулю или не существует, а при пе-

реходе через точку x0

вторая производная меняет знак,

то точка

графика с абсциссой x0

является точкой перегиба.

Доказательство.

Пусть

при

f x

0 при

x x0 . Значит, слева от точки

график выпуклый, а справа от

точки x0 вогнутый. Поэтому точка

x0 ,

f x0

графика функции яв-

ляется точкой перегиба.

Аналогично доказывается,

что если

при

x0 и

f x 0 при x

x0 ,

то точка

x0 , f

является точкой перегиба

графика функции y

x .

Точки, где функция непрерывна, а вторая производная равна нулю или не существует, называются критическими точками вто-

рого рода.

Пример 5.4. Исследовать график функции y	x4	6x2	8 на
выпуклость и вогнутость.
Решение. Находим, что y 4x3 12x ,	y	12x2	12

12 x2 1 12 x 1x 1 . Вторая производная существует на всей

числовой оси и обращается в нуль при x1		1 и x2 1. Вторая про-
изводная положительна при x	, 1	1, , следовательно, на

этих промежутках график является вогнутым. Вторая производная

отрицательна при	x	1,1 , где график функции является выпук-
лым. Точки x1	1 и x2	1 являются точками перегиба.

5.5. Асимптоты графика функции и их построение

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки по кривой от начала координат.

Асимптоты могут быть вертикальными и наклонными.

Вертикальные асимптоты появляются на границах области определения функции и в точках разрыва второго рода. Говорят, что

прямая x

a является вертикальной асимптотой графика функции

y f x

, если

lim

f (x)

или

lim

f (x)

Например,

кривая

имеет вертикальную асимптоту x 1,

так как

lim

Примером асимптоты гра-

1 0

фика функции, возникающего на границе области определения, яв-

ляется асимптота x			0 графика y ln x .
								1
	Пример 5.5. Исследовать функцию					y	e x		на наличие верти-
кальных асимптот.
				1
	Решение. Функция y e x				определена				на множестве
x	,0	0, .	Поскольку точка		x	0	оказывается выколотой

из области определения, то рассмотрим левосторонний и провосто-

ронний пределы функции при x

lim

e x

0 и

lim

e x

x 0

Функция имеет вертикальную асимптоту x

0 .

Наклонные асимптоты появляются при

и как на-

клонные прямые описываются уравнением вида

kx b . Для на-

хождения параметров

k и

рассмотрим

произвольную точку

M x, y , расположенную на кривой, имеющей наклонную асимптоту.

y		y kx b
		y kx b
		y	f x
	S
0	P	M	x
	P



	Рис. 17.

Расстояние MP от точки M до асимптоты стремится к нулю при удалении точки на бесконечность. Удобнее, однако, рассмотреть

отрезок SM

, являющийся гипотенузой прямоугольного тре-

cos

угольника MPS . Поскольку cos

не изменяется при x

, то

lim

PM lim SM cos

0 или

lim kx

b f

0 .

Выносим за скобки x и получаем

lim x

0 .

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.99 Mб43050.pdf
#
15.11.20223 Mб03053.pdf
#
15.11.20223 Mб33054.pdf
#
15.11.20223.01 Mб33109.pdf
#
15.11.20223.01 Mб23110.pdf
#
15.11.20223.04 Mб13115.pdf
#
15.11.20223.04 Mб03118.pdf
#
15.11.20223.05 Mб03119.pdf
#
15.11.20223.05 Mб03123.pdf
#
15.11.20223.06 Mб103125.pdf
#
15.11.20223.06 Mб13126.pdf