Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3115

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

3.04 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Из рис. 3 следует, что площадь треугольника

MOA S MOA,

площадь сектора

MOA Ssekt , площадь треугольника

COA

S COA

связаны неравенством

S MOA Ssekt S COA.

Поскольку

S MOA

AO MB

R R sin x

R2 sin x

, Ssekt

R2 x

OA CA

tgx

R 2tgx

COA

то имеем

R 2 sin x

R 2 x

R 2tgx

Разделим все члены на выражение

R 2 sin x

sin x

cos x

Перейдем к обратным величинам, воспользовавшись свойст-

вами неравенств,

sin x

cos x .

Так как lim

cos x 1, lim 1

1, а переменная величина

sin x

за-

ключена между двумя величинами, имеющими предел равный 1.

Следовательно, на основании теоремы 6 предыдущего параграфа

lim

sin x

Пример 2.4.

lim

sin 3x

lim

sin 3x

0 sin 5x

x 0

sin 5x

Пример 2.5.

lim

cos3x

lim

2 sin 2

3x 2

2 lim

sin 2 3x

4x2

9 4 x2

sin 2 2x

sin 2 2x 4x2

x 0 sin 2 2x

9 4 x

2.5. Число e. Второй замечательный предел

	1	1	x
Рассмотрим переменную величину			. Можно показать,
Рассмотрим переменную величину		x	. Можно показать,
		x

что эта переменная величина возрастает и ограничена. Следовательно, она должна иметь предел. Действительно,

		1		x
lim	1			e	,
lim	1		x	e	,
x			x
где e - иррациональное число (e	2,71828 ...) .
Если в равенстве положить			1/x = ,		то при x	имеем
0 и получаем
lim 1		1/		=е.
lim 1				=е.
0

При решении конкретных задач на пределы могут быть полезны модифицированные варианты записи второго замечательного предела:

		1	x		1
lim	1		e , lim	1

		x			x
x			x 0

где x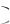является бесконечно большой величиной, а

нечно малой величиной при x

a , или при x

Пример 2.6.

lim

1 x 6

= lim

1 x

= lim

lim

= е 1=е.

e ,

x- беско-

Пример 2.7.

lim

= lim

1 x

e3.

= lim

lim

= е е

е =

Пример 2.8.

x 3

x 1 4 x 3

x 3

lim

= lim

x 1

== lim

x 1

y 4

== lim 1

lim

= e 4

e 4 .

2.6. Раскрытие некоторых неопределенностей

Рассмотрим предел функции lim

f (x)

(или при x

), кото-

x a g(x)

рый при непосредственной подстановке x

= a приходит к одному

из случаев неопределенности. Укажем приемы для решения таких примеров, приемы «раскрытия неопределенности».

1.Рассмотрим

предел

отношения

многочленов

при x

lim

Pn x

где

P x

xn 1

... a

x2 a x

n 1

Qm x

Q x

xm 1 ...

b x

b . Для раскрытия получающейся

m 1

неопределенности

необходимо вынести x в старшей степени в

числителе и знаменателе

an 1

...

lim

xn an

Qm x

bm 1

x mb

...

x m

Если m n , то предел равен отношению коэффициентов при

старших степенях

. Если же m

n , то

lim

=0.

Qm x

x m nb

В случае n

xn m a

lim

= lim

Qm x

где знак бесконечности определяется знаком коэффициента

Пример 2.9.

7x3

4x 2

lim

2x 1

lim

x 2

Здесь было использовано, что при x

величины

стремятся к нулю.

2. Если в пределе многочлены в числителе и знаменателе

стремятся к нулю, то получается неопределенность вида

для

раскрытия которой надо разложить числитель и знаменатель на множители и сократить одинаковые бесконечно малые величины.

Пусть a является действительным корнем кратности 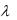многочлена, стоящего в числителе, т.е.

Pn x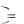x aPn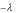 x , где Pn a 0 .

Кроме того, a является действительным корнем кратности многочлена знаменателя, т.е.

Qm x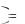x a Qm x , где Qm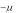 a 0 .

Если = , то

	lim	Pn x	lim	x a Pn	x	Pn	a	.
	lim		lim					.
	x a Qm x		x a x a Q		x	Qm	a
				m
Если		, то

lim

Pn x

lim

x a Pn

lim x a

0 .

Qm x

x a

x a x a Q

x a

Если

, то

lim

Pn x

lim

x a Pn

lim

Qm x

x a

x a x a Q

x a x a

Пример 2.10.

lim

2x2

lim

x(x2

2x 1) 1

x(x 2)

x 0

Пример 2.11.

lim

4x2

5x 2

lim

x 1 2 (x 2)

0 .

x 1

2x 3

x 0 x 1 (x2

x 3)

3. Если дробь является иррациональной, т.е. в числителе или знаменателе есть корни, то для раскрытия неопределенности вида

0 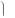необходимо выделять в качестве множителей бесконечно ма-

лые величины, не содержащие радикалов, посредством умножения числителя и знаменателя на сопряженное выражение.

Пример 2.12.


3		x	1		(3	x	1)(3 x2					3 x		1)
lim				lim
	x		1					3
										2
x 1				x 1	(x		1)(		x	2	3		x	1)
					(x		1)(		x				x	1)

lim			(x			1)		lim					1			1	.
			3							3					3
					2							2
x 1	(x	1)(		x	2	3	x 1)	x 1	(		x	2	3	x 1)
	(x	1)(		x			x 1)		(		x			x 1)

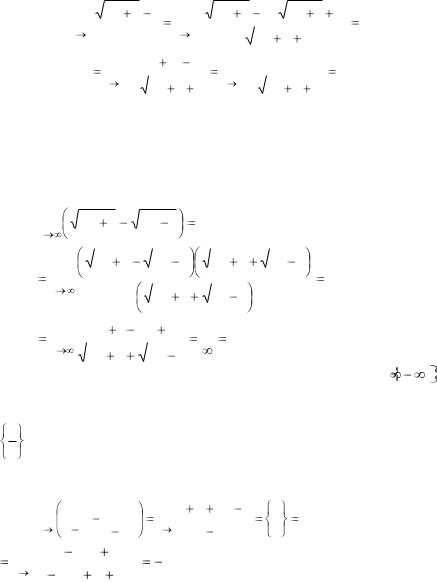
Пример 2.13.

lim	x2	1 1		lim		(	x2 1	1)(			x2	1 1)
		x
									2
x 0				x	0		x(	x	2		1	1)
							x(	x			1	1)
	lim		(x2	1)	1		lim			x2			0.


	x 0 x( x2			1 1)			x 0 x( x2				1 1)

При раскрытии неопределенности вида для представ-

ления бесконечно малых величин в удобном виде, не содержащем иррациональности, необходимо умножить и разделить на сопряженное выражение.

Пример 2.14.

lim

x2 1

lim

0 .

Раскрытие другого варианта неопределенности вида

требует приведения к общему знаменателю. В результате преобразований получим уже рассмотренный случай неопределенности

00 .

Пример 2.15.

	lim		1	3	lim	1	x x2 3		0
	lim	1 x		1 x3	lim		1 x3	0
	x 1	1 x		1 x3	x 1		1 x3	0
lim	(x 1)(x 2)				1 .

				x2 )
x 1 (1		x)(1 x		x2 )

2.7. Сравнение бесконечно малых величин

Бесконечно малые величины xи xназываются беско-

нечно малыми величинами одного порядка малости при x a , если

lim

, где C является неравной нулю константой.

Бесконечно малые величины

x называются эквива-

лентными бесконечно малыми величинами при x

a , если

lim

1. В качестве эквивалентных бесконечно малых величин

можно назвать величины x и sin x при x

0 .

Пример 2.16. Показать,

что бесконечно малые величины x

ln 1

при x

0 являются эквивалентными.

Рассмотрим

lim

ln 1

lim

ln 1

lim ln 1

x 1/ x

ln e 1.

0 x

x 0

Пример 2.17. Показать,

что бесконечно малые величины x

e x

1 при x

0 являются эквивалентными.

Рассмотрим

lim

e x

lim

x 0

y 0 ln y 1

x 0

ln 1

ln e

Бесконечно малая величина

является бесконечно малой

величиной более высокого порядка малости по сравнению с бесконечно малой величиной 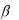x , если

lim	x	0 .

	x
x a	x

При вычислении пределов бесконечно малые величины могут заменяться эквивалентными.

2.8. Непрерывность функции в точке

Пусть функция

определена в некотором интервале

a,b . Возьмем произвольную точку

a,b . Для любого

a, b

разность

называется приращением аргумента x

точке

обозначается

x0 .

Отсюда

x .Разность

значений

функции

f x0

называется

приращением функции f(x) в точке x0 и обозначается

или f .

x0		x0	x	x
	x

Рис. 4.

Функции y 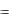f x , определенная в точке x0 и ее окрестности, называется непрерывной в точке x0 , если бесконечно малому

приращению аргумента соответствует бесконечно малое приращение функции, т.е.

lim y 0.

x 0

Можно дать второе определение непрерывности функции, следующее из первого. Для этого рассмотрим детальнее предыдущее определение.

lim	y	lim	f x	f	x0	lim	f x	lim	f x0	0 .
x	0	x	0			x	0	x	0
Воспользовавшись тем, что предел постоянной f x0										есть са-
ма постоянная, получим
			lim	f	x	lim f	x	f x0 .
			x	0		x x0

y sin x

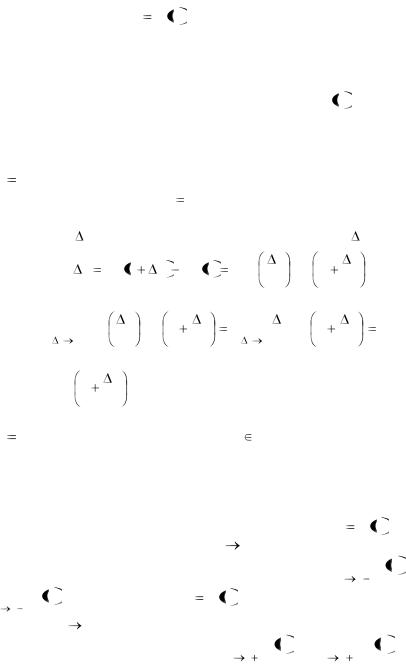
Тогда функция y f x , определенная в точке x0 и в некоторой ее окрестности, называется непрерывной в точке x0 , если суще-

ствует предел функции в этой точке, который равен значению функции точке x0 . Это означает, что при нахождении предела непрерыв-

ной функции достаточно в выражение функции f x подставить

вместо аргумента x его значение x0 .
Пример	2.18. Исследовать	на непрерывность	функцию
y sin x .
Решение.	Функция y sin x	определена при всех	действи-

тельных значениях аргумента х. Возьмем для произвольной точки х

приращение x и найдем соответствующее приращение

y :

y sin

sin x

2 sin

cos

Рассмотрим

lim

2sin

cos x

2 lim

cos

0 .

x 0

Предел равен нулю, поскольку произведение ограниченной

функции cos

и бесконечно малой величины есть бесконеч-

но малая величина. Согласно определению непрерывности функция

непрерывна в любой точке x R . По аналогии можно до-

казать непрерывность и других элементарных функций на области их определения.

	Третье определение непрерывности функции в точке связано с
понятием одностороннего предела. Предел функции									y	f x	назы-
вается левосторонним, если при					x		a	аргумент	x остается все
время меньше			a , что обозначается таким образом:						lim f		x или
									x	a
lim	f x	. Предел функции		y	f	x	называется правосторонним,
x a	0
если при		x	a аргумент x	остается все время больше a . Право-
сторонний предел записывается так:						lim		f x или	lim	f x .
						x	a	x	a	0

Функции y

f x

, определенная в точке a и ее окрестности,

называется непрерывной в точке a , если предел функции y

справа при x

a равен пределу функции слева и равен значению

функции y

f x в самой точке a :

lim

x = lim

x = f

a .

Если

функция

определена

при

и при

этом

lim

f (x)

f (a)

lim

f (x) , то говорят, что

f x

в точке

x a

непрерывна справа. Если функция определена при x

c и при этом

lim

f (x)

f (c)

lim

f (x) , то говорят, что

f x

в точке

x c

непрерывна слева.

Если функция

непрерывна в каждой точке некоторо-

го интервала a;b , то говорят, что функция непрерывна на этом

интервале. Если функция у = f (х) непрерывна в каждой точке некоторого интервала (а,b) и непрерывна на концах интервала соответственно справа и слева, то говорят, что функция непрерывна на замк-

нутом интервале или отрезке [a,b].

2.9. Точки разрыва функции и их классификация

Если в точке a не выполняется хотя бы одно из условий третьего определения непрерывности функции y 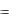f x , то точка

a является точкой разрыва. Существует три типа точек разрыва: точка устранимого разрыва, точка разрыва первого рода или скачек, точка разрыва второго рода.

Точка устранимого разрыва образуется, если функция y f x определена в окрестности точки a , но не в самой точке, а пределы функции слева и справа должны быть одинаковы, т.е.

		lim	f	x =	lim	f x .
		x a	0	x	a 0
Примером функции, имеющей подобную точку разрыва, явля-
ется функция y	sin x	, у которой точка x				0 выкалывается из об-
ется функция y	x	, у которой точка x				0 выкалывается из об-
	x

ласти определения функции, но

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.99 Mб43050.pdf
#
15.11.20223 Mб03053.pdf
#
15.11.20223 Mб33054.pdf
#
15.11.20223.01 Mб33109.pdf
#
15.11.20223.01 Mб23110.pdf
#
15.11.20223.04 Mб13115.pdf
#
15.11.20223.04 Mб03118.pdf
#
15.11.20223.05 Mб03119.pdf
#
15.11.20223.05 Mб03123.pdf
#
15.11.20223.06 Mб103125.pdf
#
15.11.20223.06 Mб13126.pdf