
2912
.pdf
Можно также рассмотреть и несколько более общий случай функций вида у = ахn. Их графики получатся из графиков функций у = xn аналогично тому, как параболы у = ах2 получались в п. 4.10 из параболы у = х2.
Можно указать на некоторые общие свойства рассматриваемых функций. Все они принимают нулевое значение при x = 0 (их графики проходят через
начало координат). При четном п = 2k функция y xn |
x2k четная, так как |
( x)2k x2k . График симметричен относительно оси Оу. |
Если п нечетное, |
n = 2k + 1, то и функция нечетная, так как 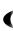 x 2k 1
x 2k 1 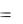 x2k 1 . В этом случае график симметричен относительно начала координат.
x2k 1 . В этом случае график симметричен относительно начала координат.
Для x >= 0 функции (4.11.1) все являются возрастающими. При этом, чем больше показатель п, тем больше значения х" для х > 1; напротив, при 0<х<1 функции с большим показателем степени п принимают меньшие значения. Для х = 1 все функции у = х" принимают значения, равные 1.
Вот таблица, поясняющая это на примере отдельных значений:
|
|
|
|
|
|
Табл.4 |
|
x |
0 |
12 |
1 |
2 |
|||
|
|||||||
y |
|
|
|
|
|||
у = х |
0 |
1 |
|
1 |
2 |
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
у = х2 |
0 |
1 |
|
1 |
4 |
|
|
|
|
4 |
|
|
|
||
|
|
|
|
|
|
|
|
у = х3 |
0 |
18 |
1 |
8 |
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
y = x4 |
0 |
116 |
1 |
16 |
|
||
|
|
|
|
|
|||
Графики функций y = xn для n = 1, 2, 3, 4 показаны на рис. 30. При п = 3 и п = 4 они соответственно называются
параболами третьей и четвертой степени (парабола третьей степени называется также кубической параболой).
4.12. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. Начнем с исследования степенной функции у = хk в случае k = 1:
y |
1 |
(4.12.1) |
|
|
|||
x |
|||
|
|
или с несколько более общей функции:
67

y |
m |
m 0 |
(4.12.2) |
|
|
||||
x |
||||
|
|
|
(в этом случае говорят, что х и у находятся в обратной пропорциональной зависимости, а число т называют
коэффициентом обратной пропорциональности). Равенство (4.12.2) записывают также в симметричной относительно х и у форме:
ху = т. |
(4.12.3) |
Таким образом, произведение величин, находящихся в обратной пропорциональной зависимости, постоянно и равно коэффициенту пропорциональности.
Проведем исследование функции (4.12.2) в случае m > 0.
1)Областью определения функции (12.2) служит вся ось Ох, кроме точки
х= 0: эта область состоит из двух бесконечных. открытых интервалов ( , 0) и
(0, + ).
2)Функция не обращается в нуль. Если х > 0, то (в силу т > 0) и у > 0, для отрицательных х функция также принимает отрицательные значения. Областью изменения функции является множество всех действительных чисел, кроме нуля.
3)Функция (4.12.2) нечетна (докажите); ее график симметричен относительно начала координат. Достаточно поэтому рассмотреть лишь ту его
часть, которая соответствует интервалу (0, + ).
График функции (4.12.2) обладает и симметрией относительно биссектрис координатных углов. Покажем, например, его симметрию
относительно биссектрисы I |
III углов. Запись (4.12.3) совершенно |
|
симметрична относительно х и у; |
поэтому, если точка M1 x1, y1 |
лежит на |
графике функции, то и симметричная с ней точка M 2 x2 , y2 |
, имеющая |
|
координаты x2 = y1, у2 = х1, лежит на том же графике; из равенства х1у1 = т следует
x2 y2 y1x1 m .
Это соображение применимо всякий раз, когда соотношение между х и у можно представить в форме, симметричной относительно х и у, т. е. в виде F (х, y) = 0, причем функция F (х, у) удовлетворяет условию F (у, x)=F(x,y).
4) При x > 0 функция (4.12.2) убывающая; действительно, из 0 x1 x2 следует т/х1 > т/х2, т. е. y1 y2 . Функция является убывающей и в интервале
(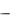 , 0) (проверьте самостоятельно). Было бы ошибкой, тем не менее считать функцию убывающей во всей области определения: в точке х = 0 она не
, 0) (проверьте самостоятельно). Было бы ошибкой, тем не менее считать функцию убывающей во всей области определения: в точке х = 0 она не
определена, имеется два интервала ее монотонности: ( |
, 0) и (0, + ), в |
каждом из которых она убывает.
5) Изучим характер изменения у при условии, что х принимает все большие положительные значения (стремится к бесконечности). Ясно, что у = т/х при этом будет приближаться к нулю, оставаясь все же положительным. Графически это означает, что кривая приближается (при движении точки вправо) к оси абсцисс, оставаясь выше оси абсцисс. Ось Ох является асимптотой графика обратной пропорциональности.
68

Если, напротив, заставить х приближаться к нулю, оставаясь положительным, то у будет неограниченно возрастать (стремиться к бесконечности). График имеет и вторую асимптоту ось Оу (последнее ясно также из наличия асимптоты Ох и симметрии относительно прямой у = х). Кривая, соответствующая разобранному случаю т > 0, показана на рис. 31, а; случай т < 0 рассматривается аналогично, график изображен на рис. 31,б.
Кривая, служащая графиком обратной пропорциональной зависимости, называется равнобочной гиперболой. В обоих случаях т > 0 и т < 0 гипербола состоит из двух отдельных частей, называемых ветвями гиперболы. Гипербола имеет оси симметрии (здесь они совпадают с биссектрисами координатных углов), две асимптоты (они совпали с координатными осями), центр симметрии (помещающийся в точке пересечения осей симметрии и асимптот).
На рис. 32 показаны графики функций y 1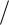 xn при n = 2, п = 3;
xn при n = 2, п = 3;
исследование этих функций предоставляется читателю.
В качестве примеров степенных функций с дробными показателями степени рассмотрим y 3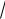 x и y
x и y 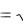
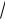 x .
x .
Функцию y 3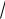 x можно рассматривать как обратную по отношению к у = х3; поэтому можно построить ее
x можно рассматривать как обратную по отношению к у = х3; поэтому можно построить ее
график как кривую, симметричную с кубической параболой у = х3 относительно биссектрисы I III координатных углов (рис. 33). Ясно, что и не зная правила, относящегося к графикам взаимно обратных
функции, мы могли бы переписать уравнение y 3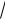 x в равносильном виде х = у3 и строить график функции х = у3 как кубической функции от у.
x в равносильном виде х = у3 и строить график функции х = у3 как кубической функции от у.
69
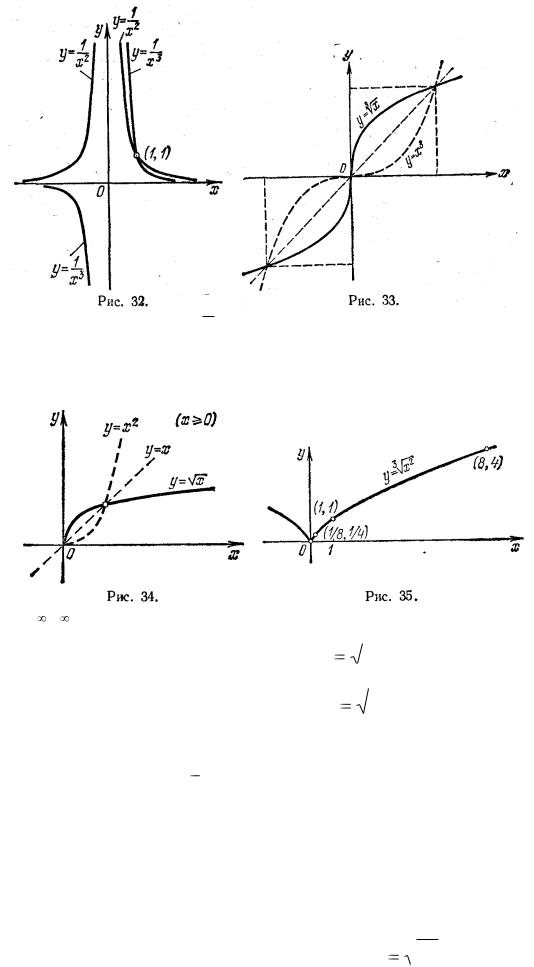
В случае функции y 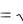
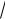 x область определения
x область определения 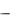 полуось x >= 0. И
полуось x >= 0. И
здесь можно применить правило, относящееся к графикам взаимно обратных функций; в самом деле, если мы рассмотрим функцию у = х2 во всей ее области
определения ( , + ), то она не будет монотонной и не будет иметь обратной функции. Возьмем, однако, функцию у = х2, ограничив область изменения х положительной полуосью (рис. 34). Теперь функция у = х2
, + ), то она не будет монотонной и не будет иметь обратной функции. Возьмем, однако, функцию у = х2, ограничив область изменения х положительной полуосью (рис. 34). Теперь функция у = х2
|
|
|
|
|
|
|
|
монотонна (на всей полуоси x >= 0) и имеет обратную функцию |
y |
|
x , график которой показан на том же |
||||
рис. 34. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Покажем еще график |
функции |
y |
3 x2 , называемый часто |
||||
полукубической параболой. |
|
|
|
|
|
|
|
Проведем краткое исследование функции. |
|
|
|
|
|
||
1) Область определения |
вся числовая ось. |
|
|
|
|
|
|
2)Функция неотрицательна и обращается в нуль только при х = 0; график функции проходит через начало координат и лежит выше оси абсцисс.
3)Функция четная, ее график симметричен относительно оси Оу.
4)Функция монотонно возрастает при положительных х (и монотонно убывает при отрицательных х, что видно, например, из симметрии графика относительно Оу).
5)При неограниченно растущем х функция также растет (стремится к
бесконечности), но медленнее, чем х; равенство y 3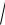 x2 влечет за собой
x2 влечет за собой
70

у/х = 1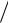 3
3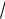 x , т. е. при х > + отношение у/х уменьшается, приближаясь к нулю.
x , т. е. при х > + отношение у/х уменьшается, приближаясь к нулю.
Это означает, что хорда, соединяющая точку (0, 0) с любой точкой (х, 3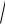 x2 ), наклонена к оси Ох по мере удаления точки в бесконечность под все более острым углом (рис. 35), график поднимается полого.
x2 ), наклонена к оси Ох по мере удаления точки в бесконечность под все более острым углом (рис. 35), график поднимается полого.
71

Исследуем еще вид кривой вблизи начала координат. Здесь при малых значениях х отношение у/х = 1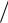 3
3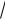 x , показывающее наклон хорды, весьма
x , показывающее наклон хорды, весьма
велико, кривая входит в начало координат, тесно приближаясь к оси Оу (касаясь оси Оу). График на рис. 35 построен с учетом этого исследования и с
использованием отдельных точек (0, 0), ( 1 |
8 |
, |
1 |
4 |
), (1, 1), (8, 4). |
|
|
|
|
||
Аналогичными приемами могут быть исследованы функции y = xk с |
|||||
любыми рациональными показателями степени. |
|||||
4.13. Показательная функция. Функция вида |
|
|
|
|
|
y |
a x |
|
|
(4.13.1) |
|
при а > 0, а 1 называется показательной функцией.
Исследуем эту функцию.
1)Областью определения функции (4.13.1) служит вся ось абсцисс, т. е. бесконечный интервал ( 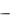 , + ).
, + ).
2)Функция (13.1) не является ни четной, ни нечетной.
3)Функция у = аx положительна при всех значениях аргумента, поэтому
ееграфик весь располагается выше оси абсцисс. Если а > 1, то a x > 1 при х > 0 и a x < 1 при х < 0. Напротив, если а < 1, то a x < 1 при х > 0 и a x > 1 при х < 0.
В любом случае a x |
1. График проходит через точку (0, 1) на оси Оу. |
x0
4)Если а > 1, то функция у = a x монотонно возрастает; если а < 1, то она
монотонно убывает. Действительно, пусть, например, а > 1. При x1 x2 имеем
y y |
2 |
a x1 |
a x2 |
a x2 a x1 x2 |
1 ; |
1 |
|
|
|
|
|
в этом выражении оба множителя положительны и |
y1 |
y2 . Аналогично доказывается убывание функции в |
|||
случае а < 1. |
|
|
|
|
|
5) Пусть а > 1; как мы видели, |
функция у |
= a x возрастает; можно |
|||
показать, что при этом ее значения по мере возрастания х становятся сколь угодно большими. График функции круто поднимается вверх при движении точки х по оси абсцисс вправо.
Если теперь заставить переменную точку х двигаться без ограничений по оси Ох влево, то при этом значения функции (4.13.1) будут становиться все меньше и меньше, оставаясь, однако, положительными. По мере неограниченного движения точки х по оси Ох влево график функции (4.13.1) будет сверху все ближе и ближе подходить к оси Ох. Ось Ох является горизонтальной асимптотой графика функции (4.13.1), как показано на рис. 36,а.
В случае а < 1 функция y = ax, как уже отмечено, убывает; по мере возрастания х ее значения быстро приближаются к нулю ось Ох является асимптотой графика функции. Отрицательным значениям х теперь соответствуют значения функции, большие единицы, с увеличением модуля х (х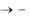 ) функция растет, стремится к бесконечности. График показательной функции при а < 1 показан на рис. 36, б.
) функция растет, стремится к бесконечности. График показательной функции при а < 1 показан на рис. 36, б.
Чем больше основание а > 1, тем круче поднимается график функции y = ax вправо и тем быстрее приближается к асимптоте при движении точки влево.
71
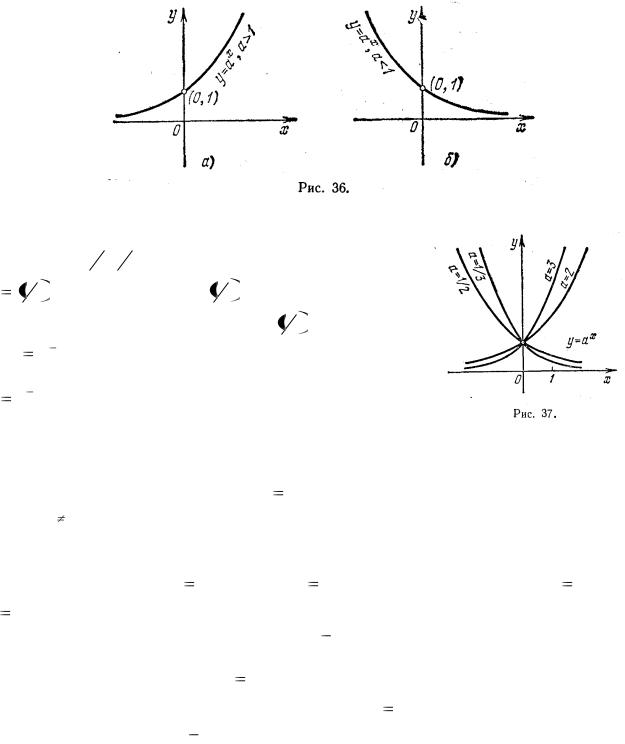
На рис. 37 показаны графики показательных функций y = ax при значениях
основания а =2,3, 1 |
2 |
, 1 |
3 |
. Заметим, |
что |
графики y = 2 x и |
||
|
|
|
|
|
|
|
||
y |
1 |
x |
(или y = 3x и у = |
1 |
x соответственно симмет- |
|||
|
|
2 |
|
|
|
|
3 |
|
ричны относительно оси Оу. Действительно, y 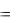 12 x можно записать
12 x можно записать
как |
y 2 x , если точка (х, у) принадлежит графику функции у = 2х, то |
|
точка (—х, у), симметричная ей относительно оси Оу, лежит на графике |
|
|
y |
2 x . |
|
|
4.14. Логарифмическая функция. Функция вида |
|
|
y loga x , |
(4.14.1) |
где а > 0 и а 1, называется логарифмической функцией. |
|
|
|
Чтобы построить график логарифмической функции, проще |
всего |
заметить, что она является обратной функцией для показательной функции.
Действительно, если y |
loga x , то x |
a y , и |
обратно. Функции y |
loga x |
x a y и взаимно обратные функции, |
их графики расположены зеркально |
|||
симметрично относительно биссектрисы I |
III координатных углов. |
|
||
Этим мы и воспользовались при построении на рис. 38 графика |
||||
логарифмической функции y loga x по известному (изображенному |
здесь |
|||
пунктиром) графику показательной функции y |
a x (рис. 38, а относится к |
|||
случаю а > 1, а рис. 38, б |
к случаю 0 < а < 1). |
|
|
|
Отметим, что графики логарифмических функций в обоих случаях расположены правее оси ординат Оу, поскольку логарифмическая функция определена лишь для положительных значений независимой переменной х. При
72
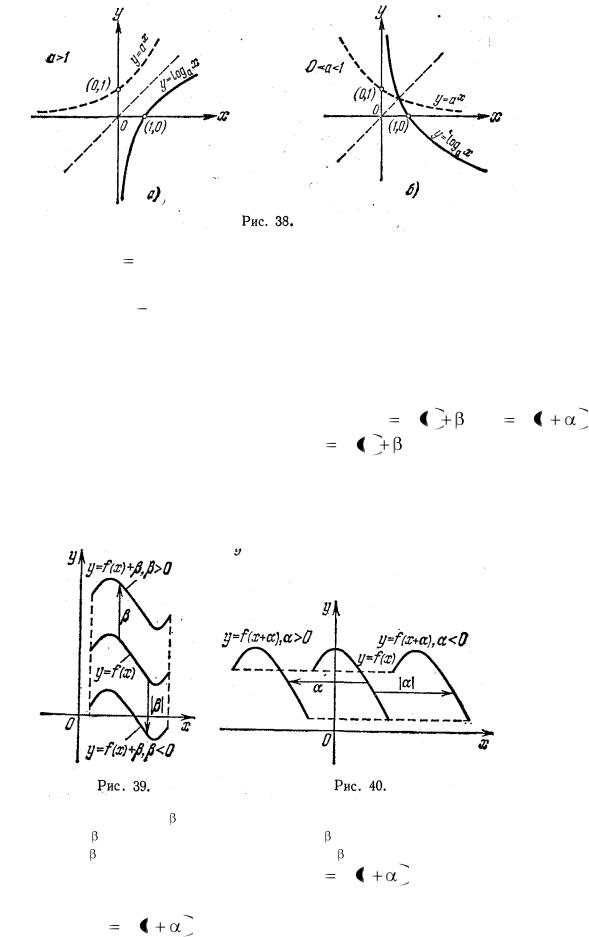
всяком основании а (а > 1 или 0 < а < 1) графики проходят через точку (1, 0). Число х = 1 служит нулем
логарифмической функции y |
loga x при любом а. |
При а > 1 логарифмическая функция (4.14.1) является возрастающей |
|
функцией, при 0 < а < 1 |
убывающей. |
5.ГРАФИКИ ФУНКИЙ
5.1.Преобразование графиков. Параллельный сдвиг графика. Во многих случаях графики функций могут быть построены путем некоторых преобразований уже известных графиков других функций более простого вида. Так, если известен график функции y = f(x), то можно построить графики функций вида
y |
f x |
; |
y f x |
. |
1) Построение графика функции y f x |
(сдвиг |
графика |
в |
|
направлении оси ординат). Вспомним, что график линейной функции у = ах + b получался из графика функции у = ах сдвигом на |b| единиц (вверх или вниз, смотря по знаку b) в направлении оси Оу (см. рис. 25). Точно так же ясно, что
ординаты графика функции у = f (х) + получаются из ординат графика функции у = f (х} прибавлением
постоянного слагаемого , т. е. для получения графика у = f (х) + |
надо весь график у = f (х) переместить |
|
параллельно оси Оу на | | единиц вверх или вниз, смотря по знаку |
(рис. 39). |
|
2) Построение графика функции y |
f x |
(сдвиг графика в |
направлении оси абсцисс). Пусть по графику функции y = f(x) нужно построить
график функции y f x |
. Эту задачу можно решить переносом графика |
|
73 |
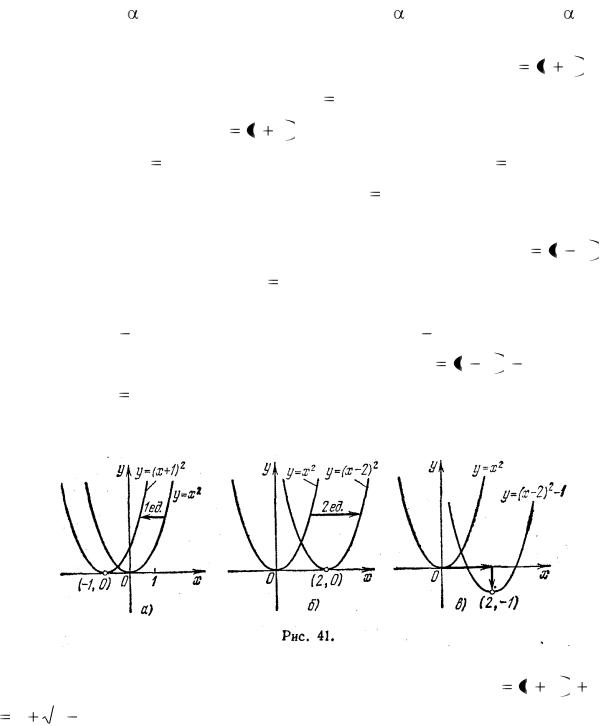
функции у = f(х) на | |
[ единиц масштаба влево, если |
> 0, и вправо, если |
< 0 |
|||||||||
(рис. 40). |
|
|
|
|
|
|
|
|
|
|
|
|
Поясним это на следующем примере. Рассмотрим функцию y |
x |
1 2 и |
||||||||||
сравним ее график с графиком функции |
y x2 . Одни и те же ординаты мы |
|||||||||||
получим, |
если для функции y |
x |
1 2 |
будем брать |
абсциссы на единицу |
|||||||
меньшие, |
чем для |
y |
x2 . Абсциссы всех точек |
графика |
y |
x2 |
следует |
|||||
уменьшить на единицу, |
т. е. сдвинуть график y x2 влево на одну единицу |
|||||||||||
масштаба (рис. 41, а). |
|
|
|
|
|
|
|
|
|
|
||
По таким же |
соображениям видно, что график |
функции |
y |
x |
2 2 |
|||||||
получится |
из графика |
функции |
y |
x2 |
сдвигом |
на |
две |
единицы |
вправо |
|||
(рис. 41,б). |
|
|
|
|
|
|
|
|
|
|
|
|
Оба |
сдвига |
в направлении осей Ох и Оу |
могут применяться |
|||||||||
одновременно. Так, |
для построения графика функции |
y x |
2 2 |
1 следует |
||||||||
график функции y |
x2 |
снести на две единицы вдоль оси Ох вправо и на одну |
||||||||||
единицу вдоль оси Оу вниз (рис. 41,в).
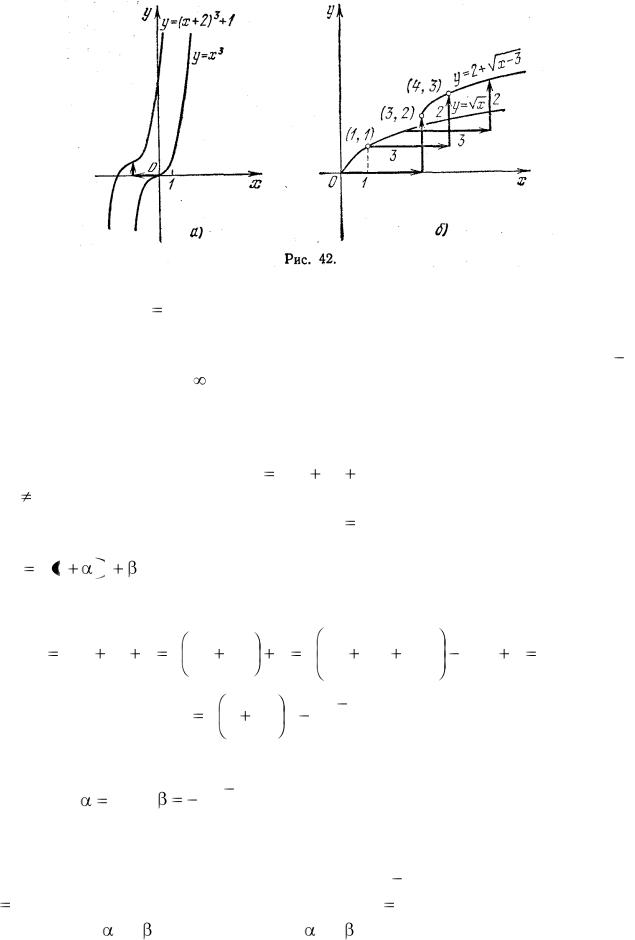
Пример. Построить графики функций: а) |
y x 2 3 1; |
|
|
|
б) y 2 |
x 3 . |
|
74
|
Решение. а) График функции у = (х + 2)3 + 1 получится из известного |
||||||||||||||||||||||||
графика функции y x3 |
(рис. 30) сдвигом на две единицы влево и на одну |
||||||||||||||||||||||||
единицу вверх (рис. 42, а). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
б) Решение понятно из рис. 42, б. Область определения функции здесь |
||||||||||||||||||||||||
бесконечный интервал [3, |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
5.2. График квадратного трехчлена. Квадратным трехчленом мы |
||||||||||||||||||||||||
назвали целую рациональную функцию второй степени (4.8.3): |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
ax2 |
|
bx |
c , |
|
|
|
|
|
(5.2.1) |
||||
где a |
0 . Докажем, что графиком квадратного трехчлена является парабола, получаемая параллельными |
||||||||||||||||||||||||
сдвигами (в направлениях координатных осей) из параболы |
y ax2 . Для этого приведем выражение (5.2.1) |
||||||||||||||||||||||||
путем простых тождественных преобразований к виду |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y |
a x |
2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(5.2.2) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Соответствующие |
преобразования, |
записанные |
ниже, |
известны как |
||||||||||||||||||||
«выделение точного квадрата»: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y ax2 |
|
bx c a x2 |
|
b |
x |
c a x2 |
|
b |
x |
b2 |
|
b2 |
|
c |
||||||||||
|
|
|
|
|
4a 2 |
|
4a 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
b |
2 |
4ac |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a |
x |
|
|
. |
|
|
|
|
(5.2.3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2a |
|
|
4a |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Мы привели квадратный трехчлен к виду (5.2.2); при этом |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
b |
, |
|
b2 |
|
4ac |
|
|
|
|
|
|
|
|
(5.2.4) |
|||||||
|
|
|
|
2a |
|
|
4a |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(эти выражения не следует запоминать, удобней всякий раз выполнять преобразование трехчлена (5.2.1) к виду (5.2.2) непосредственно).
Теперь видно, что график трехчлена (5.2.1) |
парабола, равная параболе |
||||
y ax2 и получаемая сдвигами параболы |
y |
ax2 в направлениях осей |
|||
координат на |
и |
(с учетом знака |
и |
) соответственно. Вершина этой |
|
|
|
|
|
|
75 |
