2912

Решение. а) Удобно перейти в данном выражении к дробным степеням:

Мы замечаем, что над логарифмами чисел производятся действия более простые, чем над самими числами: при умножении чисел их логарифмы складываются, при делении—вычитаются и т.д.

Именно поэтому логарифмы получили применение в вычислительной практике.

Действие, обратное логарифмированию, называется потенцированием, а именно: потенцированием называется действие, с помощью которого по данному логарифму числа находится само это число. По существу потенцирование не является каким-либо особым действием: оно сводится к возведению основания в степень (равную логарифму числа). Термин ―потенцирование‖ можно считать синонимом термина ―возведение в степень‖.

При потенцировании надо пользоваться правилами, обратными по отношению к правилам логарифмирования: сумму логарифмов заменить логарифмом произведения, разность логарифмов – логарифмом частного и т. д. В частности, если перед знаком логарифма находится какой-либо множитель,

87

то его при потенцировании нужно переносить в показатель степени под знак логарифма.

Пример 5. Найти N, если известно, что

данного равенства, перенесем в показатели степени под знаками этих логарифмов; получим

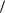loga N loga b23 loga c13 .

Теперь разность логарифмов заменим логарифмом частного:

для получения последней дроби в этой цепочке равенств мы предыдущую дробь освободили от иррациональности в знаменателе.

Свойство 7. Если основание больше единицы, то большее число имеет больший логарифм (а меньшее – меньший}, если основание меньше единицы, то большее число имеет меньший логарифм {а меньшее – больший).

Это свойство формулируют также и как правило логарифмирования неравенств, обе части которых положительны:

При логарифмировании неравенств по основанию, большему единицы, знак неравенства сохраняется, а при логарифмировании по основанию, меньшему единицы, знак неравенства меняется на противоположный.

Доказательство основано на свойствах 5 и 3. Рассмотрим случай, когда а > 1. Если N > М > 0, то N/M > 1 и, логарифмируя, получим

(a и N/M лежат по одну сторону от единицы). Отсюда log a N > log a M.

Случай а < 1, в котором из N > М > 0 следует log a N< log a M, читатель разберет самостоятельно.

3.2. Логарифмы по различным основаниям. Модуль перехода. Здесь мы установим некоторые свойства, относящиеся к логарифмам по различным основаниям. Для удобства продолжим нумерацию свойств п. 3.1.

Свойство 8. При возведении основания в некоторую (ненулевую) степень логарифм делится на этот показатель степени:

откуда

88

Следствие. При возведении основания и числа в одну и ту же (ненулевую) степень логарифм не изменяется.

Доказательство. Последовательно применяя свойства 8 и 6, находим

Решение. Перепишем данное выражение, сведя основания логарифмов к 5:

Свойство 9. Если а, N положительны и оба не равны единице, то

loga N logN a = logN N = 1.

Свойство 9 доказано.

Следующее важнейшее свойство дает общее правило перехода от логарифмов с основанием а к логарифмам с другим основанием b:

Свойство 10. Имеет место следующее равенство:

логарифмов по основанию а к логарифмам по основанию b. Доказательство. Напишем снова основное тождество

89

и прологарифмируем обе его части по основанию а:

logb N loga b loga N .

Отсюда прямо вытекает требуемое равенство (3.2.3).

Пример 3. Упростить выражение logb a logc b loga c .

Решение. В силу (3.2.4) и (3.2.2) имеем

logb a logc b loga c = logc a loga c 1.

Упражнения:

90

8. Вычислить: loga2 blog a 3b .

4.ФУНКЦИИ И ГРАФИКИ

4.1.Величина. Числовые множества. При изучении природы и в трудовой деятельности человеку приходится иметь дело с многими разнообразными величинами. К ним, в частности, относятся длина, площадь, температура, время, сила, скорость и т. д. Вообще под величиной обычно понимают объект, который может быть охарактеризован числом в результате измерения, т. е. в результате сравнения с объектом той же физической природы, принятым за единицу измерения.

В тех или иных физических процессах могут участвовать несколько величин, причем одни из них могут изменять свои числовые значения, а другие нет. Первые из них будем называть переменными, а вторые—постоянными, хотя такое разделение величин более или менее условно.

Для математики свойственно абстрагироваться от физической природы рассматриваемых величин; величина характеризуется множеством принимаемых ею числовых значений. Если это множество сводится к одному единственному значению, то величина называется постоянной; если множество

еезначений состоит более чем из одного элемента, то величина называется переменной. Здесь и дальше мы ограничим себя действительными величинами, множества значений которых состоят исключительно из действительных чисел.

Множество значений, принимаемых переменной величиной, называется

ееобластью изменения.

Приведем несколько примеров. Число сторон многоугольника может иметь значения 3, 4, 5,.... Частное от деления числа, не равного нулю, на модуль этого же числа может принимать только два значения: + 1 и -1. Квадрат действительного числа может быть равен любому неотрицательному числу.

Вообще, область изменения переменной величины х может быть произвольным числовым множеством. Если величина принимает только натуральные значения 1, 2, 3,..., то ее называют целочисленной переменной. Часто приходится рассматривать переменные, множество значений которых представляет собой некоторый (конечный или бесконечный) интервал числовой оси.

Уточним в связи с этим понятие интервала (или промежутка).

Пусть а, b два действительных числа, причем а < b. Тогда можно рассматривать следующие виды интервалов.

Открытым интервалом (а, b) называется множество действительных чисел х, удовлетворяющих неравенствам а < х < b, т. е. совокупность всех точек числовой оси, лежащих строго между точками а и b (концы исключаются). Интервал (Х0 - h, X0 + h) длины 2h с серединой x0 называется окрестностью (h- окрестностью) точки Х0.

Замкнутым интервалом или сегментом [а, b] называется множество действительных чисел х, удовлетворяющих неравенствам а <= х <= b, т. е. совокупность всех точек, расположенных между а и b, включая а и b.

Иногда рассматриваются полуоткрытые интервалы [а, b) и (а, b], соответственно определяемые неравенствами a <= x < b, а < x <= b.

91

Бесконечный интервал (а, ) определяется как множество действительных чисел х, удовлетворяющих неравенству х > а; в случае неравенства х >= а бесконечный интервал обозначают [а, ). Вся числовая ось также может рассматриваться как бесконечный интервал и обозначаться через

(- , ).

4.2. Определение функции. Геометрия, механика, физика, различные области науки и техники дают нам множество примеров, когда рассматриваемые в том или ином вопросе переменные величины находятся в зависимости, так что значение одной из величин определяет значение другой. Площадь круга полностью определяется величиной его радиуса: S = R2. Скорость точки, движущейся равноускоренно, зависит от времени по закону v=v0 +at . Давление идеального газа при постоянном объеме V0 изменяется в зависимости от температуры: P=RT/V0 . Во всех указанных примерах, несмотря на различие смысла входящих в них величин, есть нечто общее: задание значения одной из двух рассматриваемых переменных величин определяет значение второй величины. Такого рода зависимости между двумя переменными называют функциональными зависимостями.

Сформулируем определение понятия функции: переменная у называется функцией переменной х, если каждому значению х (из некоторой области Х изменения х) поставлено в соответствие по определенному закону значение у.

При этом х называется независимой переменной (иногда аргументом), а область

изменении х, называется, как обычно, областью изменения у.

В принятом определении функции существенны два момента:

во-первых, в нем указана область изменения Х независимой переменной х, и, во-вторых, в нем требуется наличие определенного правила соответствия между у и х.

Тот факт, что у есть функция от х, выражают в записи так: y f x

(произносится: «игрек есть эф от икс»). Буквой f в этом равенстве обозначен именно закон соответствия

между х и у.

Схематически можно изобразить это так: будем рассматривать две числовые оси х и у (рис. 11); пусть X область определения функции y=f(x). Каждой точке х из этой области ставится в соответствие некоторая точка оси у (закон соответствия условно изображается стрелкой).

Значение функции y=f(x), соответствующее определенному значению х=x1 из области определения функции, обозначается. так:

92

всех значениях х.

Найти: а) f (1); б) f 2 / 2 ; в) f (а); г) f(2/x).

При одновременном рассмотрении нескольких различных функций используют различные буквы для обозначения каждого из законов

Две функции считают равными (совпадающими), если их области определения совпадают и значения при любых одинаковых значениях аргумента равны.

Пример 2. Функции f(x)=2 и (х) = 1 + sin2 x+ cos2 x совпадают; нет

93

показаны точки с абсциссами х, х0, х1, их ординаты соответственно равны у, у0, 0. График показан на интервале [а, b); то, что точка х = b исключена, условно показано стрелкой в правом конце кривой линии графика функции y = f (x).

График функции дает удобное и наглядное представление о ее свойствах, и ниже уделено много внимания методам построения графиков функций.

Определение функции не дает указания на то, в какой форме задан закон соответствия между значениями аргумента и зависимой переменной; практически привычной формой задания этого закона является для нас запись функциональной зависимости в виде некоторой математической формулы, например:

В этом случае говорят, что функция задана аналитическим выражением. При этом термин «аналитическое выражение» имеет приблизительно тот же смысл, что и «алгебраическое выражение», с той разницей, что при записи аналитического выражения не ограничиваются только алгебраическими действиями (т. е. рациональными действиями и операцией извлечения корня), но пользуются, например, такими действиями, как логарифмирование, отыскание синуса или тангенса данного значения аргумента и т. п. Вообще, при определении новой математической операции для нее вводится специальный символ, который в дальнейшем уже можно использовать для записи аналитического выражения.

Для функции, заданной аналитическим выражением, область определения может состоять только из значений х, входящих в о. д. з. этого выражения. Область определения функции оказывается в этом случае частью области допустимых значений аналитического выражения, задающего функцию, или совпадает с этой областью. Например, площадь S круга, как функция радиуса R, задается выражением S = R2. Область определения этой функции по смыслу дела есть 0 < R < ; взятое же само по себе аналитическое выражение R2 определено при всех значениях R. Если функция задана аналитическим выражением относительно аргумента х и область определения не указана, то подразумевают, что область определения совпадает с о. д. з. задающего ее выражения.

Иногда функция задается разными аналитическими выражениями в разных частях области определения. Самый простой пример: будем рассматривать |х| как функцию от х. Тогда

способами и в разных видах.

Кроме аналитического способа задания применяют графическое и табличное задание функций. Если функция задана графиком, то можно по чертежу находить значения у, отвечающие данным значениям х, разумеется, приближенно.

Табличный способ задания функции заключается в том, что для

94

соответствующие значения у (с определенной степенью точности). Небольшой фрагмент таблицы может выглядеть так:

В данном примере шаг таблицы равен 0, 02.

Графическое и табличное задание функций часто возникает в результате проведения измерений, опытов, применения самопишущих приборов.

Для многих функций, заданных аналитически, также составлены таблицы, облегчающие применение этих функций (таблицы квадратных и кубических корней, таблицы логарифмов, тригонометрических функций и др.). Необходимо приобрести навыки в пользовании таблицами функций.

4.4. Элементарное исследование поведения функции. Систематическое и полное исследование функций составляет одну из главных задач области математики, называемой математическим анализом. В

элементарной математике также рассматривают простейшие вопросы, связанные с исследованием функций.

При этом под исследованием функции понимают установление ряда ее свойств. Итогом такого исследования может быть построение графика функции. В связи с этим вспомним некоторые понятия, относящиеся к функциям.

а) Нулем (или корнем) функции f (х) называется такое значение аргумента х, при котором функция обращается в нуль. Графически нули функции суть точки пересечения ee графика с осью Ох (например, точка

х1 на рис. 12).

б) Функция f(х), область определения которой симметрична, относительно начала отсчета О (например, является сегментом [- а, а]), называется четной, если для любого х из ее области определения выполнено равенство

95

График четной функции симметричен относительно оси Оу (рис. 13), так как вместе с точкой {х, f (х)} ему будет принадлежать и симметричная точка

(- х, f (x)). Обратно, если график симметричен относительно оси Оу, то функция четная.

в) Функция f (x), область определения которой на оси Ох симметрична относительно начала О, называется нечетной, если для любого x из ее области определения выполнено равенство

График нечетной функции симметричен относительно начала координат, так как вместе с любой его точкой (х, f (х)) ему принадлежит и симметричная точка ( х, f (х)) (рис. 14). Обратно, если график функции симметричен относительно О, то функция нечетная.

Примеры четных и нечетных функций:

Многие функции, например у = х2 + x, у = sin х + cos х не являются ни четными, ни нечетными функциями.

г) Функция называется возрастающей в некотором промежутке, лежащем в ее области определения, если для любых двух значений x1, х2, из этого промежутка из неравенства х1 < х2, следует f (x1) < f (x2) (большим значениям аргумента отвечают большие значения функции). Если из х1 < х2 следует лишь неравенство f (x1) <= f (x2), то функция называется неубывающей. Аналогично, убывающей называется функция, для которой из х1 < х2 следует f (x1) > f (x2), а невозрастающей функция, для которой при х1 < х2 выполняется неравенство f (x1) >= f (x2). Интервал, на котором функция убывает или возрастает, называется интервалом монотонности функции. Так, например, для функции, график которой изображен на рис. 12, интервалами монотонности служат интервалы (а, x0) и (x0, b) (на первом из них функция монотонно возрастает, на втором монотонно убывает).

Функция y = x x , которая также может

является неубывающей функцией на всей числовой оси. Она возрастает на положительной полуоси (рис. 15).

д) Точка x0 называется точкой максимума (минимума) функции y = (x), если функция определена в самой этой точке и в некоторой окрестности точки x0 выполняется неравенство

На рис. 16 точки x1, x3 суть точки максимума, а точки x2, x4 точки минимума функции. Максимум функции ее наибольшее значение по сравнению с «соседними» точками слева и справа, но не обязательно по сравнению с отдаленными точками. Практически, если находятся интервалы монотонности, то на их стыке часто обнаруживаются точки максимума или минимума, как на рис. 16. Термин «экстремум» функции объединяет понятия максимума и минимума:

точки x1, x2, x3, x4 суть точки

экстремума функции f (x).

е) Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность. На рис. 17, а прямые х = 1 и у = 0 асимптоты графика функции. На рис. 17, 6 показан график с асимптотой у = х (биссектриса первого координатного угла).

При исследовании функции необходимо ответить на следующие вопросы.

96