2912

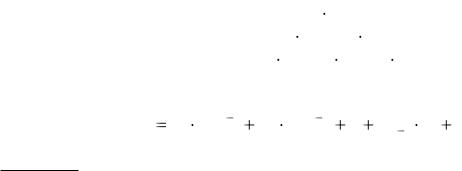
I. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

1.1.Натуральные числа. Натуральные числа выражают количество подлежащих счету однотипных или не однотипных предметов; таковы, например, числа один, два, десять, двадцать,…, сто, двести пятьдесят шесть, тысяча и т. д.

Понятие натурального числа относится к простейшим, первоначальным понятиям математики и не подлежит определению через другие, более простые понятия.

Натуральные числа могут быть естественным образом расположены по их возрастанию; каждое следующее натуральное число получается из предыдущего прибавлением единицы. Записанные в порядке возрастания;

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ....

натуральные числа образуют натуральный ряд. Многоточие показывает возможность неограниченного продолжения этого ряда. В этом смысле говорят, что имеется бесконечное множество натуральных чисел. Единица – наименьшее натуральное число; наибольшего числа натуральный ряд не имеет.

Напомним принцип записи натуральных чисел в десятичной системе счисления при помощи десяти цифр

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Цифры, участвующие в записи числа, при чтении их справа налево указывают последовательно, сколько в данном числе содержится единиц, затем десятков, сотен, тысяч и т. д. Вообще, цифра, стоящая на i-м месте, считая справа, покажет, сколько данное число содержит единиц разряда 10m-1. Так,

где c1, c2, ..., cm – цифры, при помощи которых число a m записывается в виде c1c2 ... cm (здесь черта сверху ставится, чтобы не смешивать число a m с произведением чисел c1, c2, ..., cm).

Замечание. Десятичная система счисления – не единственно возможная. В древности (в Вавилоне) использовалась система счисления, в которой, наряду с десяткой, в основу было положено число 60 (шестидесятеричная система счисления). Ее влияние сохранилось до сих пор в делении часа на 60 минут, окружности на 360 градусов и т. д. В настоящее время при использовании электронных вычислительных машин, в процессе программирования применяются двоичная и восьмеричная системы счисления. Приведем для примера запись нескольких чисел в троичной системе. В этом случае используем только три цифры 0, 1, 2 в их обычном смысле. Число 3 в троичной системе играет роль десятки в десятичной системе счисления и должно обозначаться

49

как 10. Вместо 32 = 9 будем писать 100 и т. д. Вот запись нескольких чисел в

Вдальнейшем мы будем пользоваться исключительно десятичной системой счисления.

Варифметике и алгебре рассматривают различные действия над числами:

сложение, вычитание, умножение, деление, возведение в степень, извлечение корня и т. д. Первые четыре из этих действий называют арифметическими или рациональными. Но только два из них – сложение и умножение – безусловно выполнимы в области натуральных чисел: сумма и произведение натуральных чисел суть снова натуральные числа.

Сформулируем законы, которым подчиняются действия сложения и умножения; строгие определения этих действий и обоснование их свойств (выводимых из небольшого числа аксиом) рассматриваются в теоретической арифметике и здесь опускаются.

—от перестановки слагаемых сумма не изменяется. Переместительный (или коммутативный) закон умножения:

—от перестановки сомножителей произведение не изменяется. В дальнейшем, по большей части, в записи произведения a b точку опускаем и пишем просто ab .

Сочетательный (или ассоциативный} закон сложения;

—сумма не зависит от группировки слагаемых.

Этот закон позволяет записывать сумму нескольких слагаемых без скобок. Например:

a b c a b c a b c

Сочетательный (или ассоциативный) закон умножения;

—произведение не зависит от группировки сомножителей.

Этот закон позволяет писать произведение нескольких сомножителей без

50

Этот закон лежит в основе правила раскрытия скобок, которым часто пользуются в вычислениях и преобразованиях.

1.2. Простые и составные числа. Признаки делимости.

Если а и b—натуральные числа, причем a=bq,

где q—также натуральное число, то говорят, что q—частное от деления числа а па число b, и пишут: q=a/b. Также говорят, что а делится на b нацело или без остатка. Всякое число b, на которое а делится без остатка, называется делителем числа а. Само число а по отношению к своему делителю называется кратным. Таким образом, числа, кратные b, суть числа b, 2b, Зb, ...

Числа, кратные числу 2 (т. е. делящиеся на 2 без остатка), называются четными. Числа, не делящиеся на 2 нацело, называются нечетными. Каждое натуральное число либо четно, либо нечетно.

Если каждое из двух чисел а1, а2 является кратным числа b, то и сумма а1+ а2 – кратное числа b. Это видно из записи

Всякое отличное от единицы натуральное число имеет по меньшей мере два делителя: единицу и самоѐ себя. Если число не имеет никаких других делителей, кроме себя и единицы, оно называется простым. Число, имеющее какой-нибудь делитель, отличный от себя и единицы, называют составным числом. Единицу принято не относить ни к простым, ни к составным числам. Вот несколько первых простых чисел, записанных в порядке возрастания:

2, 3, 5, 7, 11, 13, 17, ...

Число 2 – единственное четное простое число; все остальные простые числа – нечетные.

То, что простых чисел имеется бесконечное множество, было установлено еще в древности (Евклид, III век до нашей эры).

Идея доказательства Евклида бесконечности множества простых чисел весьма проста. Допустим, что простых чисел – конечное число; перечислим их

Очевидно, что это тело не делится ни на одно из чисел (1.2.1). Следовательно, либо оно само является простым, либо, если оно составное, то имеет простой делитель, отличный от чисел (1.2.1), что противоречит допущению о том, что в записи (1.2.1) перечислены все простые числа.

Это доказательство представляет большой интерес, так как дает пример доказательства теоремы существования (бесконечного множества простых

51

чисел), не связанного с фактическим отысканием объектов, существование которых доказывается.

Можно доказать, что всякое составное число представимо в виде произведения простых чисел. Так, например,

(причем p1 повторяется множителем k1 раз, p2 повторяется множителем k 2

раз и т. д.). При этом условии можно доказать, что разложение единственно с точностью до порядка записи сомножителей.

При разложении числа на простые множители полезно бывает использовать признаки делимости, позволяющие выяснить, делится ли данное число на некоторое другое число без остатка, не производя самого деления. Мы выведем признаки делимости на числа 2, 3, 4, 5, 9.

1. Признак делимости на 2. На 2 делятся те и только те числа, в записи которых последняя цифра выражает четное число (0, 2, 4, 6 или 8).

Доказательство. Представим число в виде C1C2 ...Cm

C1C2 ...Cm C1C2 ...0 Cm .

Первое слагаемое в правой части делится на 10 и потому – четное; сумма будет четной тогда и только тогда, когда Cm – четное число.

2. Признак делимости на 4. Число C1C2 ...Cm делится на 4 тогда и только

тогда, когда двузначное число, выражаемое его последними двумя цифрами, делится на 4.

Доказательство. Представим число C1C2 ...Cm в виде

C1C2 ...Cm C1C2 ...00 Cm 1Cm .

Первое слагаемое делится на 100 и тем более на 4. Сумма будет делиться на 4 в том и только в том случае, если Cm 1Cm делится на 4.

3.Признак делимости на 5. На 5 делятся те и только те числа, запись которых заканчивается цифрой 0 или цифрой 5.

Рекомендуем читателю доказать этот признак самостоятельно.

4.Признаки делимости на 3 и на 9. Число делится на 3 (соответственно на 9) в том и только в том случае, когда сумма его цифр делится на 3 (соответственно на 9).

Доказательство. Запишем очевидные равенства

10 = 9 + 1,

100 = 99 + 1,

1000 = 999 + 1,

…………………

в силу которых можно число C1C2 ...Cm представить в виде

52

Видно, что все слагаемые, кроме, быть может, последней скобки, делятся на 9 (и тем более на 3). Поэтому данное число делится на 3 или на 9 тогда и только тогда, когда делится на 3 или на 9 сумма его цифр C1 C2 ... Cm .

1.3. Наибольший общий делитель и наименьшее общее кратное. Если каждое из натуральных чисел а, b, ..., f делится нацело на натуральное число - k, то говорят, что число k является их общим делителем. Так, числа 108 и 144 имеют общие делители 1, 2, 3, 4, 6, 9, 12, 18, 36. Если два или несколько чисел не имеют общих делителей, отличных от единицы, то эти числа называются взаимно простыми. Так, числа 49 и 121 взаимно простые.

Так как данные числа а, b, ..., f могут иметь лишь конечное число общих делителей, то среди их общих делителей имеется наибольший; в случае взаимно простых чисел он равен единице.

Для наибольшего общего делителя (н.о.д.) применяется обозначение

(а, b, ..., ) = d.

Например:

(108, 144) = 36; (49, 121) = 1; (60, 36, 42) = 6.

Наибольший общий делитель двух чисел можно находить, пользуясь их разложением на простые множители. Пусть требуется, например, найти н.о.д. чисел 504 и 540. Разложим каждое из них на простые множители:

504 = 23 32 7,

540 = 22 33 5.

Мы видим, что, кроме единицы, общими делителями данных чисел являются

2, 22, 3, 32, 2 3, 22 3, 2 32, 22 32.

Таким образом,

(504, 540) = 22 32 = 36.

В общей форме процесс отыскания н.о.д. можно описать на примере двух чисел следующим образом. Запишем разложение данных чисел а и b на попарно различные простые множители:

Может случиться, что среди чисел p1, р2,..., рn нет ни одного, равного кому-либо из чисел q1, q2, …, qm. Тогда а и b—взаимно простые, (a, b) = 1. Если, например, р1 совпадаете одним из чисел q1, q2, …, qn, то оба числа а и b делятся на р1, взятое в степени, меньшей из двух степеней, с которыми это число p1 входит в разложение каждого из чисел а и b. Поэтому для получения н.о.д. чисел а и b следует: 1) выбрать все одинаковые простые множители, входящие в разложения а и b; 2) каждый из них взять в степени, меньшей из двух степеней, с которыми этот множитель входит в указанные разложения; 3) взять

53

произведение найденных таким путем общих множителей – оно и будет н.о.д. чисел а и b.

Подобным же образом находится и н.о.д. нескольких чисел. Имеется и иной метод отыскания н.о.д. двух чисел; о нем рассказывается в п. 4.

Если число т является кратным для каждого из чисел а, b, ..., f (т. е. делится на любое из этих чисел нацело), то т называется общим кратным чисел а, b, ..., f. В частности, произведение нескольких натуральных чисел всегда является их общим кратным. Среди всех общих кратных данных чисел а, b, ..., f имеется наименьшее; оно называется наименьшим общим кратным (н.о.к.) данных чисел и обозначается так:

a,b,...,f m .

Н.о.к. двух или нескольких чисел также удобно находить, используя разложение этих чисел на простые множители. Так, для чисел

504 = 23 32 7, 540 = 22 33 5

мы найдем н.о.к., взяв каждый из простых множителей в их разложениях в большей из двух степеней, в которых он входит в эти разложения:

[504, 540] = 22 33 57 = 7560.

Аналогично,

[150, 180, 240] = 24 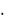32 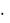52 = 3600.

Итак, для отыскания н.о.к. нескольких чисел следует: 1) выписать все простые множители, входящие в разложение хотя бы одного из этих чисел; 2) взять каждый из этих простых множителей в наибольшей из степеней, в которых он входит в разложения данных чисел; 3) взять произведение найденных степеней простых сомножителей – оно и будет н.о.к. данных чисел.

Нетрудно заметить, что для двух взаимно простых чисел а и b

[a, b] = ab

– н.о.к. двух взаимно простых чисел равно произведению этих чисел. Отметим,

без доказательства, более общее соотношение (оно сводится к предыдущему в случае, если (а, b) = 1:

[a, b] (a, b) = ab,

имеющее место для любых двух чисел: произведение наибольшего общего делителя на наименьшее общее кратное двух чисел равно произведению этих чисел.

1.4. Целые числа. Рациональные числа. Если сложение и умножение натуральных чисел всегда приводят вновь к натуральному числу, то уже вычитание не всегда выполнимо, если оставаться в области арифметики натуральных чисел. Для возможности образования разности любых двух натуральных чисел возникает необходимость расширить совокупность чисел,

вводя нуль и целые отрицательные числа —1, —2, —3, ..., —п, ... Натуральные числа называются также целыми положительными числами. Если хотят подчеркнуть, что данное число положительное, то перед ним ставится знак ―+”, но, как правило, пишут не +4, а просто 4 и т. д., перед отрицательными же числами знак ―–‖ ставится обязательно. Число нуль не относят ни к отрица-

54

тельным, ни к положительным числам. Числа п и —п называют

противоположными.

Вся совокупность целых чисел

…, –n, …, –2, –1, 0, 1, 2, …, n, …

состоит из целых положительных (натуральных) чисел, целых отрицательных чисел и нуля.

Теперь уже, во множестве всех целых чисел, действие вычитания (так же как и сложения) всегда выполнимо. При этом, действие вычитания может быть сведено к сложению с числом, противоположным вычитаемому:

Таким образом, произведение двух чисел одного знака есть положительное число, двух чисел противоположного знака – отрицательное число. Число, противоположное данному, равно произведению данного числа на минус единицу.

Произведение любого числа на нуль равно нулю.

Множество чисел, обладающее тем свойством, что сумма, разность и произведение двух любых чисел этого множества снова ему принадлежат, называется числовым кольцом. В числовом кольце неограниченно выполнимы целые рациональные действия, т. е. рациональные действия, кроме, быть может, деления. Натуральные числа не образовали числового кольца, так как действие вычитания не всегда приводило вновь к натуральному числу. Целые числа образуют числовое кольцо, кольцо целых чисел.

Множество чисел, в котором выполнимы все рациональные действия, включая и деление (кроме деления на нуль, которое невозможно), называется числовым полем. Целые числа не образуют поля, так как в области целых чисел деление не всегда выполнимо.

Всвязи с этим множество целых чисел вновь расширяют до множества рациональных чисел. Рациональным числом называется число, представимое в виде a / b где числитель a – целое, а знаменатель b – натуральное число. Если а делится на b нацело, то рациональное число – целое; в противном случае рациональное число называется дробным. Оно считается положительным, если a – положительное, и отрицательным, если а – отрицательное.

Дробь a / b можно сократить, разделив числитель и знаменатель на н.о.д. чисел а и b. В дальнейшем, как правило, при записи рационального числа в виде a / b дробь a / b считается несократимой, т. е. а и b полагаются взаимно простыми числами.

Вобласти рациональных чисел неограниченно выполнимы все рациональные действия (кроме деления на нуль): сумма, разность, произведение и частное рациональных чисел также являются рациональными

55

числами. Поэтому рациональные числа образуют числовое поле – поле рациональных чисел.

Практически правила действий над рациональными числами хорошо известны из арифметики. Для сложения и умножения справедливы те же

Разность между данным числом и его целой частью называется дробной частью числа. Дробная часть числа х равна х - [х] и иногда обозначается через

как целое число совпадает со своей целой частью. Для любого числа его дробная часть неотрицательна и строго меньше единицы:

0 x – [ x ] < 1.

Всякое рациональное число однозначно разлагается на сумму целой и дробной частей, например:

С разложением рационального числа на целую и дробную части связано понятие деления (натуральных чисел) с остатком. Число а/b однозначно представляется в виде суммы своей целой части [a/b] = q и дробной части h (не исключено, что целая или дробная часть равна нулю):

использовать для такого более формального определения понятий частного и остатка. Пусть a, b – натуральные числа. Два целых неотрицательных числа q, r называются соответственно частным и остатком от деления а на b, если выполняется равенство (1.4.1) и неравенство 0 r b .

На процессе деления с остатком основывается способ отыскания н.о.д. двух чисел; исторически он связан с теорией измерения отрезков у Евклида и носит название алгоритма Евклида.

56