III. Уравнения параболического типа

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2910.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.58 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

∂u

0 ≤ x <

∂t

t =0

l − x,

1 ≤ x ≤ l.

∂2u

+ sinπx ,

t > 0 ,

0 < x < l ,

u |

x=0

= u |

x=l

= 0 ,

∂t2

∂x2

u |

0 ,

∂u

= 0 .

∂t

t=0

∂2u =

∂2u + (4t −

8)sin 2x ,

t > 0 ,

0 < x < π ,

∂t2

∂x2

u |

x=0

= u |

x=l

= 0

, u |

= 0 , ∂u

= 0 .

t =0

∂t

∂2u

t=0

10.

t > 0 ,

< x < l ,

= 0, u |

= t

, u |

= 0 ,

∂t2

∂x2

x=0

x=l

t =0

∂u

= 0 .

∂t

t=0

∂2u

t > 0

0 < x < l ,

u |

= 0 ,

∂u

= A = const ,

11.

x=0

∂t2

∂x2

∂t

x=l

u |

0 ,

∂u

= 0 .

∂t

t=0

Ответы

1.u(x,t)= 12 [e−(x−at )2 + e−(x+at )2 ]+ sinaat cos x .

2.u(x,t)= 21a [arctg(x + at)− arctg(x − at)].

4. u(x,t)= sin 3lπ xcos 3πla t . 77

5.u(x,t)= πla sin πl xsin πla t .

6.u(x,t)= (sin t + cost)sin x .

7.u(x,t)= 4l2 ∑n ((−1)k +)1 sin (2k −1)πa t . aπ3 k =1 2k −1 3 l

8. u(x,t)= π12 (1−cosπt)sin πx .

sin 2t

+ t −

9. u(x,t)= 2cos 2t −

2 sin 2x .

∞

10. u(x,t)=

∑

(−1)

sin

πn xsin

πn t .

n=1

∞

k +1

(2k +1)π

11. u(x,t)= Ax +

8lA2

∑

(−1)

sin

xcos

t .

k =0

(2k +1)

(Указание. Положите

u = v + Ax ,

где

– новая неизвестная

функция)

∫ f (ϕ)dϕ,

∫ f (ϕ)cos nϕ dϕ,

Уравнения с частными производными параболического типа возникают при изучении процессов теплопроводности и диффузии.

1. Уравнение теплопроводности

Рассмотрим задачу распространения тепла в среде. Обозначим через u(x, y, z,t) температуру среды в точке

M (x, y, z) в момент времени t. Считая среду изотропной, обозначим через ρ(M ) ее плотность, через c(M ) — удельную теплоемкость и через k(M ) — коэффициент

теплопроводности в точке М. Внутри тела может возникать или поглощаться тепло (например, вследствие химической реакции). Обозначим через F(M ,t) плотность источников

тепла в точке М в момент времени t.

Подсчитаем баланс тепла в произвольном объеме V за промежуток времени (t,t + dt). Пусть S — граница области V и

n — вектор внешней нормали поверхности S . Если температура тела неравномерна, то в нем возникают тепловые потоки. Согласно закону Фурье, через поверхность S в объем V поступает количество тепла

Q1 = ∫∫k	∂u dSdt = ∫∫(k grad u,n0 )dSdt ,
S	∂n	S

где n0 — орт внешней нормали к поверхности S. Применяя к интегралу справа теорему Гаусса—Остроградского, будем иметь

Q1 = ∫∫∫div(k grad u)dvdt .

Q2 = ∫∫∫F(x, y, z,t)dvdt .

Пусть температура в объеме V за промежуток времени (t,t + dt) возросла на величину

u= u(M ,t + dt)−u(M ,t)≈ ∂∂ut dt .

Всилу физических закономерностей, определяющих процесс распространения тепла, для такого изменения температуры необходимо затратить количество тепла, равное

Q3 = ∫∫∫cρ ∂∂ut dvdt .

Применяя закон сохранения энергии,

Q3 = Q1 + Q2 ,

и потому

		∂u
∫∫∫ div(k grad u)+ F − cρ		dvdt = 0 .
V		∂t

Отсюда, в силу произвольности объема V, получаем уравнение

распространения тепла

cρ

∂u

= div(k grad u)+ F(M ,t).

(1)

∂t

Если среда однородна (величины c ,

ρ и k

постоянны), то

уравнение (1) принимает вид

∂u

= a2

u + f ,

(2)

где

∂t

f =

u ≡

∂2u

cρ

∂x2

∂y2

∂z2

Уравнение (2) называется уравнением теплопроводности. Аналогично выводится уравнение диффузии частиц.

Как и в случае уравнения колебаний, для полного описания процесса распространения тепла необходимо задать начальное распределение температуры u(M ,t) в среде

(начальное условие) и режим на границе этой среды (граничные условия).

Мы ограничимся изучением уравнения теплопроводности с одной пространственной переменной

∂u = a2 ∂2u + f (x,t),

∂t ∂x2

(распространения тепла в линейных телах).

2.1. Задача Коши для уравнения теплопроводности

Рассмотрим однородное уравнение теплопроводности

∂u = a2 ∂2u , ∂t ∂x2

отвечающее случаю f (x,t)≡ 0 , т. е. отсутствию источников. Задача Коши ставится так: найти функцию u(x,t), удовлетворяющую уравнению

∂2u	= a2 ∂2u	, t > 0 , − ∞ < x < +∞,	(1)
∂t2	∂x2
		80

и начальному условию

u |t =0 =ϕ(x), − ∞ < x < +∞. (2)

Физический смысл задачи состоит в определении температуры однородного бесконечного стержня в любой момент времени t > 0 по известной его температуре ϕ(x) в

момент времени t = 0 . Считается, что боковая поверхность стержня теплоизолирована, так что через нее тепло из стержня не уходит.

Предположим, что

1)u(x,t) и ϕ(x) — достаточно гладкие функции,

убывающие при x2 + t2 → +∞					настолько быстро,			что
существуют преобразования Фурье
v(ξ,t)=	1	∫−∞+∞u (x,t)e−i ξ xdx ,						(3)
	2π
~	1		+∞			−iξx	dx ;	(4)
ϕ(ξ)=	2π		∫−∞	ϕ(x)e			dx ;	(4)
	2π

2) законны операции дифференцирования

21π ∫−∞+∞ ∂dx2u2 e−iξ xdx = dvdt ,

1 ∫+∞ ∂2u e−iξ xdx = −ξ2v(ξ,t).

2π −∞ dx2

Тогда, применяя преобразование Фурье к обеим частям уравнения (1) и условию (2), от задачи (1)-(2) перейдем к задаче Коши для обыкновенного дифференциального уравнения

∂v	+ξ2a2v = 0 ,		(5)
∂t	~	(ξ)
			(6)
v \|t =0 =ϕ

(величина ξ играет роль параметра). Решение задачи (5)-(6) имеет вид

~	(ξ)e	−ξ 2 a	2t	.	(7)
v(ξ,t)=ϕ	(ξ)e			.	(7)
Ранее мы установили, что
F [e−a x2 ]=				2
F [e−a x2 ]=	1	e− ξ4a			,
	2a

где F(f ) — преобразование Фурье функции f (x).

Отсюда, полагая t = 4a12α , получаем

	1	−	x2
e−ξ 2 a2t = F	1	e	4a 2t .
a	2t

Таким образом, в правой части равенства (7) стоит произведение преобразований Фурье функций ϕ(x) и

1e−4a 2t .

a 2t

Пользуясь теоремой о свертке, в силу которой

F[f1 f2 ]= 2π F[f1 ] F[f2 ],

равенство (7) можно представить в виде

(ξ)e

−ξ 2 a 2t

−

4a 2t

. (8)

v(ξ,t)=ϕ

2π

F ϕ(x)

Левая часть формулы (8) есть преобразование Фурье (по аргументу x ) искомой функции u(x,t), так что формулу (8) можно переписать так:

			F[u(x,t)]=	1			−	x2
			F[u(x,t)]=	1	F	ϕ(x) e		4a 2t	,
			2a	πt

откуда, пользуясь выражением для свертки функций ϕ(x) и
	−	x2
e	−	4a 2t , имеем
e		4a 2t , имеем
		82

u(x,t)=	1		∫−∞+∞ϕ(λ)e−	(x−λ)2
u(x,t)=	1	πt	∫−∞+∞ϕ(λ)e−	4a 2t dλ , t > 0 .	(9)
2a		πt

Полученная формула дает решение исходной задачи (1)-(2) и называется интегралом Пуассона.

В самом деле, можно доказать, что для любой непрерывной и ограниченной функции ϕ(x) функция u(x,t), определяемая формулой (9), имеет производные любого

порядка по х и по t		при t > 0	и удовлетворяет уравнению (1)
при t > 0 и x .
Покажем, что функция			(x−λ)2
	1	∫−∞+∞ϕ(λ)e−
u(x,t)=				dλ , ϕ(x) C(− ∞,+∞), (9)
			4a 2t
2a	πt

удовлетворяет начальному условию u |t =0 =ϕ(x), − ∞ < x < +∞.

Положим

x − λ = μ . 2a t

Тогда λ = x − 2a tμ ; dλ = −2a tdμ , так что

u(x,t)=	1	∫−∞+∞ϕ(x − 2a tμ)e−μ2 dμ ,
	π
откуда при t → +0 получим
u(x,t)=	1	∫−+∞∞ϕ(x)e−μ2 dμ =ϕ(x),
	π

так как

∫−+∞∞ e−μ2 dμ = π .

Сформулируем следующий важный результат. Теорема 1. В классе ограниченных функций

u(x,t)= {u(x,t) < M , − ∞ < x < +∞, t > 0}

решение задачи Коши (1)-(2) единственно и непрерывно зависит от начальной функции.

Пример. Найти решение задачи Коши
∂2u	∂2u	,		t > 0 , − ∞ < x < +∞,					′
∂t2	= ∂x2	,		t > 0 , − ∞ < x < +∞,					(1 )
	u \|t =0 = e		−		x2	, − ∞ < x < +∞.			′
			−		2				′
									(2 )
Пользуясь формулой Пуассона (9), получаем
		1				λ2	(x−λ)2
u(x,t)=						∫−∞+∞ e− 2 e−		dλ ,	(10)
u(x,t)=				πt		∫−∞+∞ e− 2 e−	4t	dλ ,	(10)
	2a			πt

ϕ(x)= e−π22 , a =1 .

Преобразуем интеграл в правой части. Имеем

	λ2	(x−λ
∫−+∞∞ e−	2 e−	4t

λ2

xλ

λ2

dλ = ∫−+∞∞ e−

2 e−

−

4t dλ =

−

1+2t

λ−

x 2

+∞

= e

2(1+2t ) ∫−∞

1+2t

dλ . (11)

Сделаем замену переменной
1 + 2t	λ −	x	= ξ .
	λ −		= ξ .
2t		1 + 2t

Тогда интеграл в правой части последнего равенства примет вид

2t		∫−∞+∞e−	ξ 2			2 πt
2t		∫−∞+∞e−	2	dξ =		2 πt
1 + 2t						1+ 2t
						∫−+∞∞e−		ξ2
(здесь мы воспользовались тем, что						∫−+∞∞e−		2 dξ = 2π ). Из
формулы (11) получаем, что
λ2	(x−λ)2				2	πt e−		x2
∫−∞+∞ e− 2 e−									.
∫−∞+∞ e− 2 e−		4t dλ =					2(1+2t )		.
					1 + 2t
Таким образом, решение u(x,t) поставленной задачи
определится формулой
		84

u(x,t)=	1	e−	x2
u(x,t)=	1	e−	2(1+2t )	, t > 0 .	(12)
1	+ 2t

Легко видеть, что построенная функция u(x,t)

удовлетворяет начальному условию (2'). Непосредственной проверкой легко убедиться в том, что эта функция при t > 0 удовлетворяет уравнению

∂u	=	∂2u	′
∂t	=	∂x2 .	(1 )

Замечание. Из формулы Пуассона (9) следует, что тепло


распространяется вдоль стержня мгновенно. Действительно,
пусть	начальная		температура				ϕ(x)		положительна		для
α ≤ x ≤ β и		равна нулю			вне		этого		отрезка.	Тогда	для
последующего распределения температур получаем
		u(x,t)=		1	∫αβϕ(λ)e−			(x−λ)2
								4a 2t	dλ , t > 0 ,
			2a πt			угодно малых t > 0 и сколь
откуда	видно,	что	при	сколь
угодно	больших		\|x\|	имеем		u(x,t)> 0 . Это				объясняется

неточностью теоретических предпосылок при выводе уравнения теплопроводности, не учитывающих инерциальность движения молекул. Тем не менее, уравнение теплопроводности дает хорошее количественное согласование с опытом. Более точное описание процессов переноса тепла дается так называемыми уравнениями переноса.

2.2. Фундаментальное решение уравнения теплопроводности

Функция

G(x,t,λ)=	1	e−	(x−λ)2
G(x,t,λ)=	1	e−	4a 2t	,
2a		πt

входящая в формулу Пуассона (9), называется фундаментальным решением уравнения теплопроводности.

Рассматриваемая как функция аргументов x , t, она удовлетворяет уравнению ut = a2uxx , в чем можно убедиться непосредственной проверкой. Фундаментальное решение

имеет важный физический смысл, связанный с понятием

теплового импульса.

Допустим, что начальное распределение ϕ(x) температур

таково:

если

x − x0

< ε,

ϕ(x)=ϕε (x)

= 2ε

если

x − x

> ε.

Тогда в силу (9) распределение температур u(x,t),

t > 0 ,

стержне будет иметь вид

(x−λ)2

u(x,t)=

∫xx0−+εε e−

4a 2t

dλ .

(13)

По теореме о среднем

2ε

πt

~ 2

x +ε

−(x−λ)

−

(−x−λ )

∫x00−ε

4a2t dλ = 2εe

4a 2t

+ε], так что из (13) имеем

где λ [x0 −ε, x0

(x−λ )

e−

~ 2

u(x,t)=

4a 2t

πt

Переходя в последнем равенстве к

пределу при

ε → 0 ,

получим

(x−x0 )2

u(x,t)= 1

e−

4a2t

= G(x,t, x ).

πt

Это означает, что функция G(x,t, x0 ) представляет

распределение температур в стержне в момент t > 0 ,

если в

начальный момент t = 0

в точке

x = x0

имелся бесконечный

пик температур

(при

ε → 0

функция

ϕε (x)→ +∞), а

остальных точках стержня температура была равна нулю. Такое начальное распределение температур может быть

приближенно	реализовано следующим образом: в момент
t = 0 к точке	x = x0 стержня на очень короткий промежуток

времени подносится узкое пламя очень высокой температуры (тепловой импульс плотности cρ ).

Это начальное распределение температур описывается так

называемой δ - функцией		Дирака, обозначаемой символом
δ(x − x0 ). Не являясь функцией в обычном смысле, δ -функция
определяется формально при помощи соотношений
0,	при	x ≠ x0 ,
1)δ(x − x0 )=	при	x = x0 ;
+ ∞,
2) ∫αβδ(x − x0 )dx =1		на любом интервале (α, β),

содержащем точку x0 .

Основным свойством, определяющим δ -функцию,
является следующее: для всякой непрерывной функции f (x)
β	f (x ),		если	x (α, β),
∫α f (x)δ(x − x0 )dx =		0	если	0
		0,		x0 (α, β).
Таким образом,	фундаментальное решение G(x,t, x0 )

является решением уравнения теплопроводности в бесконечном стержне при начальном распределении температуры ϕ(x)= δ(x − x0 ).

График функции G(x,t, x0 ) при различных значениях t > 0

имеет вид (рис. 11). Кривые 1, 2, 3 соответствуют моментам времени 9 < t1 < t2 < t3 . Рисунок показывает, как выравнивается

температура в стержне после теплового импульса. Решение

(x−λ)2

u(x,t)= 2a1 πt ∫−∞+∞ϕ(λ)e− 4a 2t dλ

задачи теплопроводности в бесконечном стержне при начальном условии u |t =0 =ϕ(x) можно рассматривать как

результат суперпозиции температур, возникающих в точке х в момент времени t вследствие непрерывно распределенных по стержню тепловых импульсов интенсивности ϕ(x) в точке λ ,

приложенных в момент t = 0 .

Рис.11

3. Распространение тепла в конечном стержне

Если стержень имеет конечную длину l и занимает отрезок 0 ≤ x ≤ l оси Ox , то для постановки задачи о распространении тепла в таком стержне помимо уравнения

∂2u	= a2 ∂2u	+ f (x,t)
∂t2	∂x2

и начального условия

u |t =0 =ϕ(x)

необходимо задать еще температурный режим на концах стержня x = 0 и x = l , т.е. задать граничные условия. Граничные условия могут быть различными в зависимости от температурного режима на концах стержня. Рассматривают три основных типа граничных условий.

1. На концах стержня задана температура u(0,l)= μ1(t), u(l,t)= μ2 (t),

где μ1(t), μ2 (t) — функции, заданные для отрезка времени

0 ≤ t ≤ T , в течение которого изучается процесс.

2. На концах стержня заданы значения производной

∂u		= v (t),	∂u	= ϕ	1	(x ).


			∂t
∂t		1		t =
	x=0

Эти условия возникают, если задана величина теплового потока Q, протекающего через торцевое сечение стержня. Например, если для x = l задана величина Q(l,t), то

			Q(l,t)= −k	∂u		,
			Q(l,t)= −k	∂u		,
				∂x	x=l
				∂x	x=l
откуда	∂u	= v	(t), где v (t)= −Q(l,t). Если				v (t)	(или	v (t))
откуда	∂u	= v	(t), где v (t)= −Q(l,t). Если				v (t)	(или	v (t))
	∂x	2	2	k			1		2
		x=l
		x=l

тождественно равна нулю, то говорят, что соответствующий конец стержня теплоизолирован.

3. На концах стержня заданы линейные соотношения между функцией и ее производной

∂u		= λ[u(0,t)−Q(t)],	∂u	= −λ[u(l,t)−θ(t)],

∂x	x=0		∂x	x=l

где θ(t) — известная функция — температура окружающей

среды, λ — коэффициент теплообмена. Это граничное условие соответствует теплообмену по закону Ньютона на

поверхности тела с окружающей средой, температура которой

θ(t).

Пользуясь двумя выражениями для теплового потока,

протекающего через сечение x = l , Q = h(u −θ) и Q = −k ∂∂ux ,

получаем формулировку третьего граничного условия в виде

∂u		= −λ[u(l,t)−θ(t)], λ = h .

∂x	x=l	k

Для сечения x = 0 стержня третье граничное условие имеет

вид	89

∂u		= λ[u(0,t)−θ(t)],
∂u		= λ[u(0,t)−θ(t)],
∂x	x=0		∂u
∂x	x=0
поскольку для теплового потока − k				при x = 0 имеем
			∂n
		∂u = −	∂u
		∂n	∂x	x = 0 противоположна
(внешняя нормаль к стержню в конце				x = 0 противоположна

по направлению с осью Ох).

Перечисленные основные задачи далеко не исчерпывают возможных краевых задач для уравнения

ut = a2uxx + f (x,t).

Например, на разных концах стержня могут задаваться условия разных типов. Мы ограничимся рассмотрением первой смешанной задачи для уравнения теплопроводности.

Задача ставится так: найти решение u(x,t) уравнения

	∂u = a2 ∂2u		+ f (x,t)	(1)
	∂x	∂x2	u(x,t) C2 {0 < x < l,t > 0},
в области	0 < x < l ,	t > 0 ,	u(x,t) C2 {0 < x < l,t > 0},
удовлетворяющее начальному условию
	u \|t =+0 =ϕ(x),		0 ≤ x ≤ l ,	(2)
и граничным условиям
	u \|x=0 = μ1(t), u \|x=l		= μ2 (t), t ≥ 0 .	(3)
Считаем,	что функция	u(x,t)	непрерывна в	замкнутой

области D = {0 ≤ x ≤ l, 0 ≤ t ≤ T} (рис.12), для чего необходимо, чтобы функции ϕ(x), μ1(t), μ2 (t) были непрерывными и выполнялись условия согласования ϕ(0)= μ1(0),ϕ(l)= μ2 (l).

Замечание. Как и для уравнений гиперболического типа, функция u(x,t) ищется только для 0 < x < l и t > 0 (но не при

t = 0 , x = 0 и t = 0 , x = l , где значения функции u(x,t) заранее задаются начальными и граничными условиями).

Сформулируем принцип максимального значения.

	Рис.12
Теорема 2.	Если функция u(x,t) C(D),					удовлетворяет
уравнению теплопроводности		∂u	= a	2 ∂2u	в	точках области
		∂t		∂x2

{0 < x < l,0 < t ≤ T}, то максимальное и минимальное значения
функции u(x,t)	достигаются или в начальный момент времени

t = 0 , или в точках границы на отрезках x = 0 или x = l . Физический смысл этой теоремы очевиден: если

температура тела не превосходит некоторого значения М в граничных точках или в начальный момент, то внутри тела (источники отсутствуют!) не может возникнуть температура, больше чем М.

Как следствия из принципа максимального значения вытекают теоремы.

Теорема 3 (единственности). Решение задачи (1)-(3) в прямоугольнике {0 < x < l,0 < t ≤ T} единственно.

Теорема 4. Решение задачи (1) -(3) непрерывно зависит от начальных и граничных функций.

4. Метод Фурье для уравнения теплопроводности

Займемся решением первой смешанной задачи для
уравнения теплопроводности: найти решение u(x,t)											уравнения
∂2u	= a2 ∂2u + f (x,t), t > 0 , 0 < x < l ,										(1)
∂t2		∂x2
удовлетворяющее начальному условию
	u \|t =0 =ϕ(x),							0 ≤ x ≤ l ,			(2)
и граничным условиям
u \|x=0 = μ1(t),				u \|x=l = μ2 (t), t ≥ 0 .							(3)
1. Начнем с простейшей задачи: найти решение u(x,t)
однородного уравнения
		∂u		= a			2	∂2u		,	(4)
		∂t		= a				∂x2		,	(4)
		∂t						∂x2
удовлетворяющее начальному условию
		u \|				=ϕ(x)					(5)
			t =0
и нулевым (однородным) граничным условиям
		u \|x=0 = 0 , u \|x=l = 0 .									(6)
Будем искать нетривиальные решения уравнения (4),
удовлетворяющие граничным условиям (6), в виде
		u(x,t)= T (t)X (x).									(7)
Подставляя u(x,t) в форме (7) в уравнение (4), получим
	T (t)X (x)			= a T (t)X (x),
		′					2			′′
							2
или		′				′′
		′				′′
		T (t)			X		(x)
			=						= −λ ,		(8)
		a2T (t)	=		X (x)				= −λ ,		(8)

откуда имеем два обыкновенных дифференциальных уравнения

′	2	λT = 0 ,	(9)
T (t)+ a
′′			(10)
X	(x)+ λX (x)= 0 .

Чтобы получить нетривиальные решения u(x,t) вида (7), 92

удовлетворяющие граничным условиям (6), необходимо найти нетривиальные решения уравнения (10), удовлетворяющие граничным условиям

X (0)= 0 , X (l)= 0 .	(11)
Таким образом, для определения функции	X (x) мы

приходим к задаче на собственные значения: найти те значения параметра λ , при которых существуют нетривиальные решения задачи

′′

(10)

(x)+ λX (x)= 0 ,

X (0)= 0 ,

X (l)= 0 .

(11)

Эта задача была рассмотрена в предыдущей главе. Там

было показано, что только при

λ =

nπ 2

(n =1,2,...)

существуют нетривиальные решения

Xn (x)= sin

nπ

задачи (10)-(11).

При λ = λn общее решение уравнения (9) имеет вид

nπa 2

T (t)

= a

e−

( an — произвольные постоянные). Функции

nπ a 2

nπ

un (x,t) = ane−

t sin

x (n =1,2,...)

удовлетворяют уравнению (4) и граничным условиям (6). Образуем формальный ряд

	nπa	2
∞		t sin nπ x
un (x,t)= ∑ane− l		t sin nπ x	(12)
n=1		l
Потребовав, чтобы функция u(x,t),		определяемая формулой

(12), удовлетворяла начальному условию u |t =0 =ϕ(x), получим

∞	πn x .
ϕ(x)= ∑an sin	πn x .	(13)
n=1	l

Ряд (13) представляет собой разложение заданной функции ϕ(x) в ряд Фурье по синусам в интервале (0,l). Коэффициенты

an разложения определяются по известным формулам

an =	2	lϕ(x)sin nπ xdx		(n =1,2,...).	(14)
	l	∫0	l
Предположим, что ϕ(x) C2 [0,l]				и ϕ(0)=ϕ(l)= 0 .	Тогда

ряд (13) с коэффициентами, определяемыми по формулам (14), будет сходиться к функции ϕ(x) абсолютно и равномерно. Так как

nπa		2
−		t
	l		≤1
0 < e

при t ≥1, то ряд (12) при t ≥1 также сходится абсолютно и
равномерно. Поэтому функция u(x,t)			— сумма ряда (12) —
непрерывна	в области	0 < x < l ,	t > 0 и	удовлетворяет
начальному и граничному условиям.
Остается	показать,	что функция u(x,t)		удовлетворяет

уравнению (4) в области 0 < x < l , t > 0 . Для этого достаточно показать, что ряды, полученные из (12) почленным дифференцированием по t один раз и почленным

дифференцированием по x два раза, также

абсолютно и

равномерно сходятся при

0 < x < l ,

t > 0 .

Но это следует из

того, что при любом t > 0 .

n2π 2a2

nπa

n2π2

nπa

−

0 <

e l

<1, 0 <

e l

<1,

если n достаточно велико.

Единственность решения задачи (4)-(6) и непрерывная

зависимость решения от начальной функции ϕ(x) были уже

установлены ранее. Таким образом,

для

t > 0

задача (4)-(6)

поставлена корректно; напротив, для отрицательных t задача

эта некорректна.

Замечание. В отличие от волнового уравнения

∂2u	= a	2	∂2u	,
∂t2	= a		∂x2	,
∂t2			∂x2
уравнение
∂u	= a	2 ∂2u
∂t	= a		∂x2
∂t			∂x2

несимметрично относительно времени t: если заменить t на -t, то получаем уравнение другого вида

∂u = −a2 ∂2u . ∂t ∂x2

Уравнение

∂u = a2 ∂2u ∂t ∂x2

описывает необратимые процессы: мы можем предсказать, каким станет данное u через промежуток времени длиной t, но мы не можем с уверенностью сказать, каким было это u за время t до рассматриваемого момента. Это различие между предсказанием и предысторией типично для параболического уравнения и не имеет места, например, для волнового уравнения: в случае последнего заглянуть в прошлое так же легко, как и в будущее.

Пример. Найти распределение температуры в однородном

стержне длины π ,		если начальная температура	стержня
u \|t =0 = sin x	(0 ≤ x ≤ π )	и на концах стержня поддерживается
нулевая температура.
Задача сводится к решению уравнения
	∂2u	= a2 ∂2u , t > 0 , 0 < x <π ,	(15)
	∂t2	∂x2
при начальном условии
и граничных условиях		u \|t =0 = sin x , 0 ≤ x ≤π ,	(16)
и граничных условиях		95
		95

u |x=0 = 0 , u |t =π = 0 , t ≥ 0 .

(17)

Применяя метод Фурье, ищем нетривиальные решения уравнения (15), удовлетворяющие граничным условиям (17), в виде

u(x,t)= T (t)X (x).

(18)

Подставляя u(x,t) в форме (18) в уравнение (15) и разделу

переменные, получим

′

′′

T (t)

X (x)

= −λ

a2T (t)

X (x)

откуда

′

λT (t)= 0

(19)

T (t)+ a

′′

(20)

X (x)+ λX (x)= 0 ,

X (0)= X (π )= 0 .

(21)

Собственные значения задачи (20)-(21) суть λ

= n2 n =1,2,...,

Xn (x)= sin nx . При

собственные

функции

λ = λn общее

решение уравнения (19) имеет вид T (t)= a

e−a 2 n2t , так что

(x,t)= a e−a2 n2t

sin nx .

Решение задачи (15)-(17) ищем в виде ряда

∞

u(x,t)= ∑ane−a 2 n2t sin nx .

(22)

n=1

Потребовав выполнения начального условия (16), получим

∞

un (x,0)= sin x = ∑an sin nx ,

n=1

откуда a1 =1,

ak = 0 (k = 2,3,...). Поэтому решением исходной

задачи будет функция

u(x,t)= e−a2t sin x .

2. Рассмотрим теперь следующую задачу: найти решение u(x,t) неоднородного уравнения

∂2u	= a2 ∂2u + f (x,t), t > 0 , 0 < x < l ,					(1)
∂t2	∂x2
удовлетворяющее начальному условию
	u \|t =0 =ϕ	(x), 0 ≤ x < l ,				(2)
и однородным граничным условиям
	u \|x=0 = 0 , u \|x=l = 0 , t ≥ 0 .					(3)
Предположим,	что функция		f (x,t) непрерывна,			имеет
непрерывную производную ∂f		и при всех t > 0 выполняется
	∂x
условие f (0,t)= f (l,t)= 0 .
Решение задачи (1)-(3) будем искать в виде
	u(x,t)= v(x,t)+ w(x,t),					(4)
где v(x,t) определим как решение задачи
	∂2u = a2 ∂2u		+ f (x,t),			(5)
	∂t2	∂x2
	v \|t =0 = 0 ,					(6)
	v \|x=0 = 0 , v \|x=l = 0 ,					(7)
а функцию w(x,t) — как решение задачи
	∂2u	= a2 ∂2u ,				(8)
	∂t2		∂x2
	w \|t =0 =ϕ(x),					(9)
	w \|x=0 = 0 ,		w \|x=l = 0 ,			(10)
Задача (8)-(10) рассмотрена в п. 1. Будем искать решение
v(x,t) задачи (5)-(7) в виде ряда
	∞			nπ
	v(x,t)= ∑Tn		(t)sin		x	(11)

	n=1			l
		nπ
по собственным функциям sin		l	x краевой задачи

	97

′′

(x)= 0

, X (0)= X (l)= 0 .

(x)+ λX

Подставляя v(x,t) в виде (11) в уравнение (5), получим

∞

′

πn

n π

x = f

(x,t),

(12)

∑ Tn

(t)+

Tn (t) sin

n=1

Разложим функцию

f (x,t) в ряд Фурье по синусам,

∞

f (x,t)= ∑ fn (t)sin nπ x ,

(13)

где

n=1

fn (t)= 2

nπ

l f (ξ,t)sin

ξdξ .

(14)

∫0

f (x,t) в

Сравнивая два разложения (12) и (13) функции

ряд Фурье, получаем

′

nπa

T (t)

= f

(t) (n =1,2,...).

(15)

T (t)+

Пользуясь начальным условием для v(x,t),

∞

nπ

v(x,0)= 0 = ∑Tn (0)sin

x , 0 ≤ x ≤ l ,

находим, что

n=1

Tn (0)= 0

(n =1,2,...).

(16)

Решения уравнений (15) при начальных условиях (16)

имеют вид:

n π a

(t −r )

−

Tn (t)= ∫0t fn (r)e

(n =1,2,...).

Подставляя найденные выражения для Tn (t) в ряд (11),

получим решение v(x,t) задачи (5)-(7)

∞

nπa

(t −r )

nπ

−

v(x,t)

= ∑n=1

fn (r)e

∫0

dr sin

x .

(17)

Функция u(x, t)= w(x, t)+ v(x,t)

будет

решением

исходной

задачи (1)-(3).						области {0 < x < l,t > 0}
3. Рассмотрим	задачу:	найти			в	области {0 < x < l,t > 0}
решение u(x,t) уравнения
	∂2u = a2 ∂2u			+ f (x,t)					(18)
	∂t2		∂x2
при начальном условии			=ϕ(x)
	u \|		=ϕ(x)						(18)
	t =0
и неоднородных граничных условиях
	u \|x=0 = μ1(t), u \|x=l = μ2 (t),								(20)
Непосредственно	метод		Фурье			неприменим			из-за
неоднородности условий (20).
Введем новую неизвестную функцию v(x,t), положив
	u(x,t)= v(x,t)+ω(x,t),
где							x
ω(x,t)= μ		(t)+[μ		2	(t)− μ (t)]		x	.
ω(x,t)= μ		(t)+[μ			(t)− μ (t)]			.
	1					1	l
							l

Тогда решение задачи (18)-(20) сведется к решению задачи

(1)-(3), рассмотренной в п. 2, для функции v(x,t).

Упражнения

1. Задан бесконечный однородный стержень. Покажите, что если начальная температура

	ϕ(x)= u0e−σ 2 x2 , − ∞ < x < +∞
( u0 > 0 ,	σ > 0 − const ), то в любой момент t > 0 температура
стержня
	u(x,t)=	u0	e−	σ 2 x2
	u(x,t)=	u0	e−	1+4a 2σ 2t	.
		1 + 4a2σ 2t
2.	Концы стержня	длиной π	поддерживаются при

температуре, равной нулю. Начальная температура

определяется формулой	u(x,0)= 2sin 3x .
	99

Определите температуру стержня для любого момента времени t > 0 .

3. Концы стержня длиной l поддерживаются при температуре, равной нулю. Начальная температура стержня определяется формулой

u(x,0)= 3sin				π l −5sin					2π	x .
u(x,0)= 3sin				π l −5sin						x .
					x				l
Определите температуру стержня для любого момента
времени t > 0 .			длиной l поддерживаются при
4. Концы стержня			длиной l поддерживаются при
температуре, равной нулю.						Начальное распределение
температуры
	2u0	x,		0 ≤ x ≤			l	,
		x,		0 ≤ x ≤				,
	l					2			(u0 = const).
ϕ(x)=	l				l	2			(u0 = const).
	2u0	(l	− x),		l	< x ≤ l,
	l	(l	− x),	2		< x ≤ l,
	l			2

Определите температуру стержня для любого момента времени t > 0 .

u(x,t)= 2e−9a2t sin 3x .

Ответы

−a 2π 2

4a 2π 2

u(x,t)= 3e

l 2

t sin π x −5e−

sin

2π x .

l 2

(4k + 2)π

4u0

∞

cos

(4k +2)2 π 2 a 2

4. u(x,t)=

e−

t .

−

∑

l 2

k =0

(2k +1)

IV. Уравнения эллиптического типа

1.Определения. Постановка краевых задач

Куравнениям эллиптического типа приводит изучение стационарных, т. е. не меняющихся во времени, процессов различной физической природы. Простейшим уравнением эллиптического типа является уравнение Лапласа

100

u ≡	∂2u	+	∂2u	+	∂2u	= 0 .	(1)
	∂x2		∂y2		∂z2

Этим уравнением характеризуется гравитационный и электростатический потенциалы в точках свободного пространства, оно описывает потенциал скорости

безвихревого потока несжимаемой жидкости, и оно же справедливо для температуры однородной изотропной среды при установившемся движении тепла.

В случае	функции	u = u(x, y) двух				независимых
переменных x ,	y уравнение Лапласа имеет вид
	u ≡	∂2u	+	∂2u	= 0 .	(2)
		∂x2		∂y2

Оно лежит в основе теории аналитических функций комплексного переменного. Его решения — действительные и мнимые части аналитических в некоторой области D функций f (z)= u(x, y)+ iv(x, y). В случае функции одного аргумента

u = u(x) имеем

u ≡	∂2u	= 0	(3)
	∂x2

Рис.13

Решениями уравнения (3) являются функции u = C1x + C2 , где

C1 , C2 — произвольные постоянные.
Определение.	Функция	u = u(x, y, z)	называется
гармонической в	области	Ω R3 , если	u C2 (Ω) и

удовлетворяет в области и уравнению Лапласа (1).

Пусть область Ω ограничена поверхностью Σ (рис. 13). Типичной для уравнения Лапласа является задача: найти функцию u(M ), M Ω , гармоническую в Ω и

удовлетворяющую на S граничному условию, которое может быть одного из следующих видов:

1. u |Σ = f1(p), p Σ, — первая краевая задача, или задача

Дирихле;
2.	∂u		= f2 (p), p Σ

	∂n		Σ

задача Неймана;
3.		∂u		= f3 (p),

			+ hu
		∂n		Σ

, — вторая краевая задача, или

p Σ, — третья краевая задача.

Здесь f1, f2 , f3 , h — заданные функции, ∂∂un — производная в

направлении внешней нормали к поверхности Σ . Геометрический смысл задачи Дирихле для одномерного

уравнения Лапласа тривиален. Одномерные гармонические функции u = C1x + C2 суть прямые линии, и задача Дирихле сводится к следующей: провести прямую через две точки

A(x1,u1 ) и B(x2 ,u2 ) (рис.14).

В зависимости от того, где ищется решение задачи — внутри области, ограниченной поверхностью Σ или в области, расположенной вне поверхности Σ , различают внутренние и внешние краевые задачи для уравнения u = 0 .

102

101

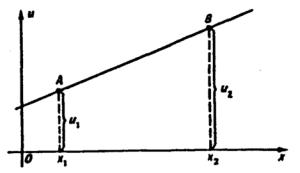
Рис. 14 Другим представителем эллиптических уравнений

является уравнение Пуассона

u = g(x, y, z),

которое отвечает равновесному состоянию под действием
внешней силы с плотностью, пропорциональной g(x, y, z).
Еще пример. Рассмотрим волновое уравнение
	u −	1	u	= 0 .	(4)
		a2
			tt
Будем искать решения уравнения (4) вида
	u = u(x, y, z,t)		= v(x, y, z)eiω t .		(5)
Подставляя функцию u в форме (5) в уравнение (4) , будем
иметь
	eiω t v +	ω2	veiω t = 0 ,
		a2
откуда
	v + k2v = 0 ,

где k = ω2	. Таким образом,	для		функции v(x, y, z)	мы

получили эллиптическое уравнение

v + k2v = 0 ,

которое называются уравнением Гельмгольца.

Как и для уравнения Лапласа, для уравнений Пуассона и

103

Гельмгольца типичными являются 1-я, 2-я и 3-я краевые задачи.

2. Фундаментальные решения уравнений Лапласа

Декартовы, цилиндрические и сферические координаты

являются наиболее употребительными. Оператор Лапласа в

декартовых координатах (x, y, z)

определяется формулой

u ≡

∂

∂2u

;

∂x2

∂y2

∂z

в цилиндрических координатах (r,ϕ, z)

∂

∂u

∂2u

u ≡

;

∂r

∂ϕ2

∂z2

в сферических координатах (r,θ,ϕ)

∂

2 ∂u

∂

∂u

∂2u

u ≡

sinθ

∂r

r2 sinθ ∂θ

r2 sin2 θ ∂ϕ2

∂r

∂θ

Большой интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической симметрией, т. е. зависящие только от переменной r .

Пользуясь сферическими координатами, видим, что
решение u = u(r),		обладающее сферической симметрией,
определяется	из		обыкновенного							дифференциального
уравнения				∂	r2 ∂u
				∂				= 0 .
								= 0 .
				∂r			∂r
Интегрируя это уравнение, находим
		u =	C1 + C			2	(C ,C		2	= const).
			r			2	1		2
			r

Полагая, например, C1 =1, C2 = 0 , получаем функцию

u0 (r)= 1r ,

которую называют фундаментальным решением уравнения

104

Лапласа в	пространстве. Функция	u0 (r)=	1	удовлетворяет
уравнению	u = 0 всюду, кроме	точки	r	r = 0 , где u0

обращается в бесконечность.

Если рассматривать поле точечного заряда e , помещенного в начало координат, то потенциал этого поля

равен u = er .

Пользуясь цилиндрическими координатами, находим, что решение u = u(r), обладающее цилиндрической или круговой симметрией (в случае двух независимых переменных),

определяется	из	обыкновенного					дифференциального
уравнения			∂		∂u
			∂		∂u
				r		= 0 ,
				r		= 0 ,
			∂r		∂r

интегрируя которое, получим

u = C1 ln r + C2 .

Выбирая C1 =1, C2 = 0 , будем иметь u0 (r)= ln 1r .

Функцию u0 (r) называют фундаментальным решением уравнения Лапласа на плоскости. Эта функция удовлетворяет

уравнению Лапласа всюду, кроме точки r = 0 , где u = ln 1r

обращается в бесконечность.

3. Формулы Грина
Будем исходить из формулы Гаусса—Остроградского
∫∫(a,n0 )dσ = ∫∫∫div adΩ	(1)

ΣΩ

Положим a = v grad u и будем считать, что функции u , v имеют непрерывные вторые производные в области Ω и

105

непрерывны вместе с первыми производными в ее замыкании

= Ω Σ , т. е.

u,v C2 (Ω)∩C1(

Имеем

∂u ,

(a,n0 )= v(grad u,n0 )= v

∂n

div a = ( ,v u)= ( v, u)+ v 2u = (grad u,grad v)+ v

u .

Поэтому из формулы (1) вытекает, что

∂u dσ .

∫∫∫{(grad u, grad v)+ v u}dΩ = ∫∫v

(2)

∂n

Это — первая формула Грина.

Меняя в формуле (2) u и v местами, получим

∫∫∫{(grad v, grad u)+u v}dΩ = ∫∫u

∂v

dσ .

(3)

∂n

Вычитая равенства (2) и (3) почленно, находим

∂v

∂u

∫∫∫{u v − v

u}dΩ = ∫∫ u

− v

dσ .

(4)

∂n

Это — вторая формула Грина.

Наконец, полагая в (2)

u = v , получим

∫∫∫{(grad u)2 + u u}dΩ = ∫∫u

∂u dσ .

(5)

∂n

Это — третья формула Грина.

Здесь всюду n — вектор внешней нормали к гладкой или кусочно-гладкой замкнутой поверхности Σ .

Граница Σ области Ω может состоять из нескольких замкнутых поверхностей. В этом случае поверхностные интегралы в правых частях формул Грина следует брать по всем поверхностям, ограничивающим область Ω .

106

		4. Основная интегральная формула Грина
Мы установили, что функция								1
					v(M )=			1	,
					v(M )=		r		,
							r
							MM 0
где rMM 0		=	(x − x0 )2 + (y − y0 )2 + (z − z0 )2							— расстояние между
точками M (x, y, z) и M0 (x0 , y0 , z0 ), удовлетворяет уравнению
Лапласа		u = 0 при M , M ≠ M0 . Пусть Ω — область в R3 с
границей Σ и u(M ) C2 (Ω)∩C1(								). Пусть M0 — некоторая
границей Σ и u(M ) C2 (Ω)∩C1(						Ω		). Пусть M0 — некоторая
внутренняя			точка	области Ω .						Поскольку	функция
v(M )=		1	разрывна в		точке			M0 Ω , непосредственно
v(M )=	rMM 0		разрывна в		точке			M0 Ω , непосредственно
	rMM 0
применить вторую формулу Грина (4)										к функциям	u и v
нельзя.					Ω \ Kε						Σ Σε ,
Рассмотрим				область	Ω \ Kε				с	границей	Σ Σε ,

получающуюся из области Ω выбрасыванием шара Kε

радиуса ε

с центром в точке M0

и поверхностью Σε

(рис. 15).

Область

Ω \ Kε

особенностей функции

v(M ) не содержит.

Применяя

вторую формулу

Грина

функциям

u(M ) и

v(M )=

в области Ω \ Kε , получаем

MM 0

−

∫∫∫ u

dΩ =

Ω\ Kε

∂ 1

∂u

∂ 1

∂u

= ∫∫ u

−

dσ + ∫∫u

dσ − ∫∫

∂n

dσ (1)

∂n r

∂n

Σε

∂n r

Σε

Преобразуем второй интеграл в правой части равенства

(1). Вычисляя производную в направлении внешней нормали к области Ω \ Kε на поверхности Σε (рис.16), найдем, что

107

Рис.15

Рис. 16

∂	1		= −	∂	1	=	1	,

							ε2
∂n r		Σε		∂r r		Σε

откуда, воспользовавшись теоремой о среднем для интеграла

108

по поверхности Σε , получим

∫∫

∂ 1

∫∫

udσ =

4πε u

= 4πu ,

(2)

∂n

ε2

dσ =

Σε

где u — среднее значение функции u(M ) на поверхности Σε .

Преобразуем теперь третий интеграл в правой части (1)

∫∫

∂u

dσ =

∫∫

∂u

dσ

4πε

∂u

(3)

∂n

= 4πε

Σε

∂n

∂u

— среднее значение нормальной производной

∂u

где

∂n

на сфере Σε . Подставляя выражения (2) и (3) в формулу (1) и

учитывая, что

в Ω \ Kε , будем иметь

MM 0

∂ 1

1 ∂u

∂u

∫∫∫ −

udΩ = ∫∫

−

dσ + 4πu

− 4πε

. (4)

Ω\ Kε

∂n r

r ∂n

∂n

Устремим теперь радиус ε

к нулю. Тогда получим:

1)limu = u(M0 ), т. к. u(M ) — непрерывная функция, а u

ε →0

—ее среднее значение по сфере радиуса ε с центром в точке

M0 ;
	∂u	= 0 , т. к. из непрерывности			первых
2) lim 4πε		= 0 , т. к. из непрерывности			первых
ε →0	∂n
производных функции u(M ) внутри Ω					вытекает
ограниченность нормальной производной
	∂u =	∂u cosα +	∂u cos β +	∂u cosγ
	∂n	∂x	∂y	∂z

в окрестности точки M0 ;

109

	ε →0			1	∫∫∫	u
3)	ε →0	∫∫∫	−	r	∫∫∫	r	dΩ по определению
3)	lim		−	udΩ = −			dΩ по определению
		Ω\ Kε			Ω

несобственного интеграла.

Врезультате указанного предельного перехода в (4) при

ε→ 0 приходим к основной интегральной формуле Грина

u(M0 )=

1 ∂u

∂ 1

∫∫Σ r ∂n

−u

−

∫∫∫Ω

dΩ. (5)

4π

∂n

4π

dσ

Таким образом, всякая функция

u(M ) C2 (Ω)∩C1(

)

представима как сумма трех интегралов

∫∫∫

dΩ,

∫∫

∂u

dσ ,

∫∫u

∂ 1

−

∂n

−

dσ ,

4π

∂n r

которые называются объемным потенциалом, потенциалом простого слоя и двойного слоя соответственно.

Если u(M ) — гармоническая в Ω функция, то								u ≡ 0 и
формула (5) принимает вид
u(M0 )=	1	∫∫Σ	1 ∂u	−u	∂ 1			(6)
	4π	∫∫Σ	r ∂n		∂n	r
							dσ
(точка M0 внутри Ω). Это —				основная формула				теории

гармонических функций. Она показывает, что значение гармонической функции в любой внутренней точке области Ω выражается через значение этой функции и ее нормальной производной на границе Σ области Ω .

Из формулы (6) следует

Утверждение. Всякая гармоническая в Ω функция u(M )

есть сумма потенциалов простого и двойного слоя.

Для уравнения Лапласа на плоскости фундаментальное решение имеет вид v0 = ln 1r . Дословно повторяя приведенные

выше рассуждения, получаем основную интегральную формулу для гармонической функции двух аргументов:

110

u(M0 )=	1		1 ∂u		−u	∂		1
	2π ∫Г	ln	r	∂n			ln	r	ds .
						∂n

Здесь Г — граница области D, n — вектор внешней нормали к границе (рис. 17). Таким образом, всякая гармоническая в области D функция u(x, y) есть сумма двух потенциалов

1				1	∂u	ds,
		∫ ln				ds,
2π		Г		r	∂n
−		1	∫u	∂			1
−	2π		∫u	∂n	ln		r	ds,
	2π		Г	∂n			r

Рис.17 логарифмического потенциала простого слоя и

логарифмического потенциала двойного слоя соответственно.

5. Свойства гармонических функций

Теорема 1. Если u(M ) — гармоническая в области Ω функция, непрерывная вместе с первыми производными в

		= Ω Σ , то ее нормальная производная	∂u	на границе Σ
	Ω	= Ω Σ , то ее нормальная производная	∂u	на границе Σ
области Ω удовлетворяет условию			∂n
области Ω удовлетворяет условию
		∫∫∂u dσ = 0 .		(1)
		Σ ∂n

В самом деле, применяя вторую формулу Грина

111

			∂v		∂u
∫∫∫{u	v − v u}dΩ = ∫∫ u			− v		dσ
∫∫∫{u	v − v u}dΩ = ∫∫ u		∂n	− v		dσ
Ω	Σ		∂n		∂n
к гармонической функции u(M )		и	к	функции v(M )≡1 ,
получаем	0 = ∫∫∂u dσ .
	0 = ∫∫∂u dσ .
	Σ ∂n
Это свойство	гармонических	функций				выражает факт

отсутствия источников внутри области Ω .

Теорема 2. Если существует решение задачи Неймана для уравнения Лапласа, то оно определено с точностью до

постоянного слагаемого.

Доказательство

проведем

при

дополнительном

предположении, что решение

u C1(

). Пусть решений два:

u1(M ) и u2 (M ). Тогда

u1 ≡ 0

≡ 0,

∂u1

= f (p)

∂u2

= f (p).

∂n

Разность u = u1 −u2

будет решением задачи

u = 0,

∂u

= 0.

∂n

Для такой функции u(M ) третья формула Грина

∫∫∫{(grad u)2 + u

u}dΩ = ∫∫u

∂u dσ

дает

∂n

∂u 2

∫∫∫

(grad u) dΩ = 0 ,

dΩ = 0

∫∫∫

∂x

∂z

∂y

В силу непрерывности и неотрицательности подынтегральной функции отсюда следует, что

112

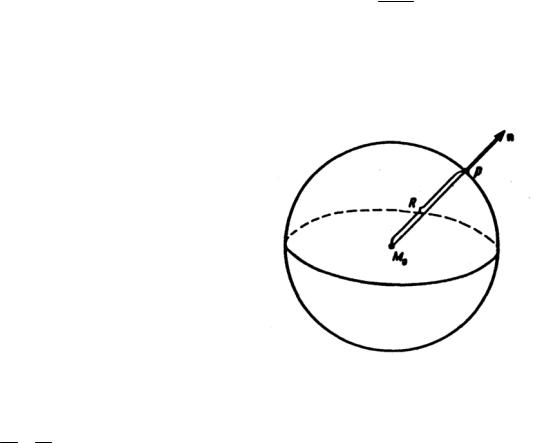
	∂u 2		∂u 2		∂u 2	≡ 0 ,
		+		+		≡ 0 ,
	∂x		∂y		∂z
или
∂u ≡ 0		, ∂u ≡ 0		, ∂u ≡ 0		в Ω ,
∂x		∂y		∂z
так что u(x, y, z)≡ 0 и, следовательно,					u1(M )−u2 (M )≡ const .
Подчеркнем, что в задаче Неймана функция f (p), p Σ,
должна удовлетворять условию
		∫∫ f (p)dσ = 0 .				(2)

Если это условие не выполнено, задача Неймана решения не имеет.

Теорема 3 (о среднем значении гармонической функции). Если функция u(M ) — гармоническая внутри шара радиуса R

с центром в точке M0 и непрерывна вместе с первыми

производными вплоть до его границы ΣR , то значение
функции u(M ) в центре M0 сферы ΣR равно среднему
арифметическому всех значений u(M ) на этой сфере,
u(M0 )=			1		Σ∫∫u(p)dσ .					(3)
			4πR2
						R
Для доказательства применим основную интегральную
формулу теории гармонических функций
u(M0 )=	1	∫∫Σ		1 ∂u		−u	∂ 1
	4π			r ∂n			∂n	r
									dσ

к сфере ΣR . Для этой сферы (рис. 18) r = M0 p = R , ∂∂n = ∂∂r и потому

113

u(M0 )=	1	∫∫Σ	1 ∂u	−u	1		(4)

	4π		R ∂n		R2
						dσ .

Всилу теоремы 1 имеем ∫∫∂u dσ = 0 , и формула (4) дает

ΣR ∂n

u(M0 )= π1 2 ∫∫u(p)dσ . 4 R ΣR

Для одномерного уравнения Лапласа ∂2u = 0 эта теорема

∂x2

является теоремой о средней линии трапеции: длина отрезка M0M равна полусумме длин отрезков аА и bВ (рис. 19).

Рис.18

114

Рис. 19 Теорема 4 (об экстремальных значениях гармонической

функции). Гармоническая в области Ω функция u(M ),

неравная тождественно постоянной, не может иметь локальных экстремумов внутри области Ω .

Будем вести доказательство методом рассуждения от противного. Пусть в точке M0 Ω функция u(M ) имеет,

например, локальный максимум. Иными словами, неравенство
u(M0 )> u(M )	(5)

выполняется во всех точках M шара достаточно малого радиуса с центром в точке M0 . По теореме о среднем значении

гармонической функции

u(M0 )= π1 2 ∫∫u(M )dσ

4 R ΣR

( ΣR — сфера в указанном шаре), откуда по теореме о среднем

для двойного интеграла получаем, что

u(M0 )= 4π1R2 4πR2u(Mcp )= u(Mcp ).

Полученное противоречие с неравенством (5) доказывает теорему.

115

Таким образом, функция u(M ), гармоническая в ограниченной области Ω и непрерывная в замкнутой области

Ω = Ω Σ , достигает своего наибольшего и наименьшего значения на границе Σ области Ω (принцип максимального значения).

Отсюда легко получаем следующие теоремы.

Теорема 5 (теорема единственности). Решение внутренней задачи Дирихле

u = 0 , u |Σ = f (p), p Σ,

непрерывное в замкнутой области Ω = Ω Σ , единственно. Пусть две функции u1(M ) и u2 (M ) являются решениями

задачи. Тогда их разность u(M )= u1(M )−u2 (M ) является

гармонической в Ω функцией, непрерывной в Ω и равной нулю на Σ . По теореме 4 об экстремальных значениях отсюда следует, что наибольшее и наименьшее значения u(M ) в Ω

равны нулю. Следовательно, u(M )= u1(M )−u2 (M )≡ 0 в Ω,

т.е. u1(M )≡ u2 (M ).

Теорема 6 (о непрерывной зависимости решений первой внутренней краевой задачи от граничных значений). Пусть u1(M ) и u2 (M ) — решения задач

u = 0,	и	u = 0,	(p),
u \|Σ =ϕ1(p)		u \|Σ =ϕ2

непрерывные в

= Ω Σ . Тогда если всюду на границе Σ

выполняется неравенство

ϕ1(p)−ϕ2 (p)

< ε, p Σ,

то всюду в области Ω

u1(M ) −u2 (M )

< ε, M Ω

Функция u(M )= u1(M )−u2 (M ) является гармонической в

Ω , непрерывна в

u |Σ =ϕ1(p)−ϕ2 (p). Поскольку

−ε <ϕ1(p)−ϕ2 (p)< ε ,

то

по

теореме 4 об экстремальных

значениях наибольшее и наименьшее значения функции u(M )

116

заключены между −ε и ε . Следовательно, u(M ) < ε , т.е. u1(M )−u2 (M ) < ε M Ω .

6. Решение задачи Дирихле для круга методом Фурье

Задача ставится так: найти функцию u(r,ϕ), удовлетворяющую внутри круга Kr0 радиуса r0 с центром в начале координат уравнению Лапласа

	u = 0 ,		(1)
непрерывную в замкнутой области			и принимающую
		Kr
	0
заданные значения на границе круга,
	u \|r =r = f (ϕ),		(2)
где f (ϕ)	0
	— достаточно гладкая функция, периодическая с

периодом 2π .

В силу однозначности искомого решения оно должно быть периодическим по ϕ с периодом 2π,u(r,ϕ)= u(r,ϕ + 2π ).

Из непрерывности решения в

следует его ограниченность

Kr .

Уравнение (1) в полярных координатах имеет вид

1 ∂

∂u

1 ∂2u

= 0 .

(3)

r2 ∂ϕ2

r ∂r

∂r

Будем искать частные решения уравнения (3) в виде

u(r,ϕ)= R(r)Ф(ϕ).

(4)

Подставляя u(r,ϕ) в форме (4) в уравнение (3),

умноженное на r2 , получим

Ф(ϕ)r

′′

+ R(r)Ф

(ϕ)= 0 ,

или

117

′′

Ф (ϕ)

= − Ф(ϕ)

= λ ,

R(r)

откуда

′′

(5)

Ф (ϕ)+ λФ(ϕ)= 0 ,

′′

′

(6)

R (r)+ rR

(r)− λR(r)= 0 .

Из

условия

u(r,ϕ)= u(r,ϕ + 2π )

получаем

Ф(ϕ)= Ф(ϕ + 2π ), а из (5) находим λ = n2

(n = 0,1,2...), так что

Фn (ϕ)= An cos nϕ + Bn cos nϕ (n = 0,1,2,...).

В частности, Ф0 (ϕ)= A0 = const .

Полагая в уравнении (6) (уравнении Эйлера) R(r)= r0 , при

A = n2 получаем

σ(σ −1)+σ − n2 = 0 .

Отсюда σ 2 − n2 = 0 ,

σ = ±n

(n > 0) и, следовательно,

(r)= a

rn + b r−n (n > 0).

При n = 0 из (6) находим

R0 (r)= a0 + b0 ln r .

Так как r−n → ∞ и

r → ∞ при

r → 0 + 0 , то для решения

внутренней

задачи

Дирихле

нужно

положить

bn = 0 ,

n = 0,1,2,... , т. е. взять R (r)= a

(n =1,2,...), R (r)= a .

Решение внутренней задачи Дирихле будем искать в виде

ряда

∞

u(r,ϕ)= A0 + ∑rn (An cos nϕ + Bn sin nϕ),

(7)

n=1

где коэффициенты An ,

Bn определяется из граничного условия

(2).

При r = r0 имеем

118

∞

u(r0 ,ϕ)= f (ϕ)= A0 + ∑r0n (An cos nϕ + Bn cos nϕ).

(8)

n=1

Запишем разложение

f (ϕ) в ряд Фурье

f (ϕ)=

∞

α0 + ∑(αn cos nϕ + βn sin nϕ),

(9)

где

n=1

α0

∫02π f (t)dt , αn =

∫02π

f (t)cos ntdt ,

βn =

∫02π

f (t)sin ntdt

(n =1,2,...).

(10)

Сравнивая ряды (8) и (9), получаем

A = α0

, A

= αn ,

B =

βn

, (n =1,2,...).

Таким образом, формальное решение внутренней задачи Дирихле для круга представимо в виде ряда

	∞			n
u(r,ϕ)= α0 +	∑		r	(αn cos nϕ + βn sin nϕ),	(11)

2	n=1	r0
где коэффициенты α0 ,α1		, β1,...αn , βn ,... определяются по
формулам (10).
При r < r0 ряд (11) можно дифференцировать по r					и ϕ
любое число раз, и, значит функция u(r,ϕ) из (11)
удовлетворяет уравнению	u = 0 .
Если предположить,	что			функция f (ϕ) непрерывна и

дифференцируема, то ряд (11) при r ≤ r0 сходится равномерно, и, следовательно, функция u(r,ϕ) непрерывна на границе

круга и удовлетворяет всем условиям поставленной задачи. Решение внешней задачи Дирихле следует искать в виде

ряда

	∞
u(r,ϕ)	= ∑	1	(An cos nϕ + Bn sin nϕ),	(12)
		n
	n=0 r
где коэффициенты	An , Bn определяются из граничного
условия u \|r =r = f (ϕ).
0
Для кольцевой	области r1 < r < r2 , образованной			двумя

концентрическими окружностями с центром в точке 0 радиусов r1 и r2 (рис. 20), решение задачи ищется в виде ряда

	∞				C
u(r,ϕ) = ∑ Anrn +					r	nn cosnϕ +
	n=1				r		(13)
∞		D					(13)
∞		D
+∑ Bnrn +		r	nn sin nϕ + A0 ln r + B0 ,
n=1		r
коэффициенты	которого			A0 , B0 , An ,Cn , Bn, Dn (n =1,2,...)

определяются из граничных условий

u(r1,ϕ)= f1(ϕ), u(r2 ,ϕ)= f2 (ϕ).

Пример. Найти функцию, гармоническую внутри круга радиуса r0 с центром в начале координат и такую, что

u |r =r0 = 3 + 5cosϕ .

Задача сводится к решению внутренней задачи Дирихле для уравнения

при граничном условии	u = 0	(14)
при граничном условии
u \|r =r	= 3 + 5cosϕ	(15)
0

Будем искать решение задачи в виде ряда

∞

u(r,ϕ)= A0 + ∑rn (An cos nϕ + Bn cos nϕ).

n=1

Из граничного условия (15) имеем

∞

u(r0 ,ϕ)= 3 + 5cosϕ = A0 + ∑r0n (An cos nϕ + Bn cos nϕ).

n=1

119	120

		Рис. 20
Отсюда в силу ортогональности системы			функций 1,
sinϕ , cosϕ ,... на отрезке [0,2π] получаем
A0 = 3 , r0 A1 = 5 , An = 0 n ≥ 0 , Bn = 0 n .
Искомое решение
u(r,ϕ)= 3 +	5	r cosϕ или u(x, y)= 3 +	5	x .

	r		r
0			0

7. Интеграл Пуассона

Преобразуем формулу (11) предыдущего параграфа к более простому виду. Подставив в нее выражения для коэффициентов Фурье и меняя порядок суммирования и интегрирования, будем иметь

∞

2π

u(r,ϕ)=

∫0

(t)

+∑

(cosntcosnϕ +sinntsinnϕ) dt =

n=1

(16)

∞

2π

∫0

f (t)

+∑

cosn(ϕ −t) dt.

n=1

Положим

для

кратности

=τ

(τ <1) и проведем

следующие тождественные преобразования:

1 +

∞

+ 1

∞

∑τ n cos n(ϕ −t)=

∑τ n [ein(ϕ−t ) + e−in(ϕ−t )

n=1

2 n=1

∞

i(ϕ−t ) n

∞

−i(ϕ−t ) n

∑(τe

)

+ ∑(τe

)

n=1

= 1

1 +

τei(ϕ−t )

τe−i(ϕ−t )

= 1

1 −τ 2

i(ϕ−t )

−i(ϕ−t )

1 −τe

1 −

τe

− 2

cos(ϕ −t)+

Подставляя это выражение в (16), получим

1 −

u(r,ϕ)=

2π

(t)

∫0

dt ,

2π

cos(ϕ −t)+ r2

1 − 2

или

− r

u(r,ϕ)=

2π

f (t)

∫0

dt .

2π

− 2rr cos(ϕ −t)+ r2

Полученная формула дает решение первой краевой задачи

для

уравнения

u = 0

внутри

круга

называется

интегралом

Пуассона,

выражение

r2 − r2

r2 − 2rr cos(ϕ −t)+ r2

называют ядром Пуассона.

Решение внешней краевой задачи имеет вид

− r

u(r,ϕ)=

2π

(t)

(r > r0 ).

∫0

2π

− 2rr cos(ϕ −t)+ r2

f (ϕ)

Можно

показать,

что

если

функция

только

непрерывна на границе круга Kr

то функция

122

121

1					r0		− r	2
		2π	f (t)			2		2
		∫0							dt при r < r0
	2π	∫0		r2	− 2rr	cos(ϕ −t)+ r2			dt при r < r0
			0		0
f (ϕ)									при r = r
								0

удовлетворяет уравнению u = 0 при r < r0 и непрерывна в замкнутом круге Kr0 .

Упражнения

Найдите функцию, гармоническую внутри круга радиуса r0 с центром в начале координат и такую, что

1.u |r =r0 = 2 + 3sinϕ .

2.u |r =r0 = sin2 ϕ .

Найдите функцию, гармоническую внутри круга радиуса r0 с центром в начале координати такую, что

3.	∂u		= Acosϕ (A = const)

	∂r		r =r
		0
4.	∂u		= 2sin2 ϕ .

	∂r		r =r
		0

5. Найдите функцию, гармоническую в кольце 1 < r < 2 и такую, что

u|r =1 =1 − cosϕ , u |r =2 = sin 2ϕ .

6.Найдите стационарное распределение температуры в

однородном секторе 0 ≤ r ≤ a, 0 ≤ϕ ≤ a .	Температура на
прямолинейных участках границы равна	нулю, а на дуге

окружности задано линейное распределение.	Указание.
Задача сводится к решению уравнения u = 0	в секторе при

граничных условиях u |ϕ=0 = u |ϕ=a = 0 , u |r =a = Aϕ (A = const).

123

Ответы

u(r,ϕ)= 2 +

sinϕ .

u(r,ϕ)=

−

cos 2ϕ .

u = A0 + Ar cosϕ , где A0

– произвольная постоянная.

4. Задача решения не имеет.

u(r,ϕ)=

ln r

1 −

−

cosϕ

−

sin 2ϕ .

ln 2

∞

(−1)k +1 r

kπ

u(r,ϕ)=

∑

sin

ϕ .

k =1

124

V. Методы решения уравнений математической физики

1. Тип и канонический вид уравнения
Постановка задачи. Определить тип уравнения
а11 (x, y)uxx + 2a12 (x, y)uxy + a22 (x, y)uyy +
+ a(x, y)ux + b(x, y)uy + c(x, y)u = f (x, y)	(1)

План решения. Тип уравнения (1) определяется знаком выражения a122 − a11a22 :

Если a122 − a11a22 > 0 в некоторой точке, то уравнений (1) называется уравнением гиперболического типа в этой точке; Если a122 − a11a22 < 0 в некоторой точке, то уравнение (1)

называется эллиптическим уравнением в этой точке;

Если a122 − a11a22 = 0 в некоторой точке, то уравнение (1)

называется уравнением параболического типа в этой точке. Замечание. Уравнение (1) может менять свой тип при

переходе из одной точки в другую. Например, уравнение yuxx + utt = 0 является уравнением эллиптического типа в

точках (x, y), y > 0, параболического типа в точках (x, y), y > 0, параболического типа в точках (x,0) и гипербо-

лического				типа			в	точках			(x, y), y > 0, Действительно,
a2	− a	a	22	= y и a2 − a a					22	< 0 при y > 0, a2 − a a			22	= 0 при
12	11		22				12	11	22		12	11	22
y = 0 и a2				− a	a	22	< 0	при y < 0.
			12	11		22
	Чтобы привести уравнение (1) к каноническому виду,
нужно сделать в нем замену переменных:
	x, y a ξ = h1 (x, y),							η = h2 (x, y),						(2)
	где													h1 (x, y) и
	● в случае уравнения гиперболического типа													h1 (x, y) и
h 2 (x, y)−общий интеграл уравнения характеристик
	a11(x, y)(dy)2 − 2a12 (x, y)dydx + a22 (x, y)(dx)2											= 0;		(3)
										125

● в случае уравнения параболического типа h1(x, y)−общий интеграл уравнения характеристик (3) и h 2 (x, y)- произвольная дважды дифференцируем функция, не выражающаяся через h1 (x, y);

● в случае уравнения эллиптического типа h1 (x, y) и

h 2 (x, y)− вещественная и мнимая части любого из двух общих интегралов уравнения характеристик (3).

1.Определяем коэффициенты уравнения a11 , a12 и a22 .

2.Вычисляем выражение

a122 − a11a22

иопределяем области его знакоопределенности.

3.Делаем вывод о типе уравнения (1).

4.Находим общие интегралы уравнения характеристик

(3).

5.В уравнении (1) делаем замену переменных (2). При этом по правилу дифференцирования сложной функции

u x a uξξx = uηηx , uy a uξξ + uηηy ,

uxx a uξξξx2 + 2uξηηx + uηηηx2 + uξξxx + uηηxx ,

u xy a uξξξxξy + uξη (ξxηy +ξyηx )+ uηηηxηy + uξξxy + uηηxy, u x a uξξx = uηηx2 + 2uξηξyηy + uηηηy2 + uξξyy + uηηyy.

В результате замены переменных уравнение (1) примет один из трех канонических видов:

● в случае уравнения гиперболического типа uξη = F1 (ξ,η,u,uξ ,uη );

● в случае уравнения параболического типа uηη = F2 (ξ,η,u,uξ ,uη );

● в случае уравнения эллиптического типа uξξ + uηη = F3 (ξ,η,u,uξ ,uη ).

Записываем ответ.

126

Пример 1. Определить тип уравнения

uxx − 4uxu − 21uyy + 2ux −3u y + 5u = x2

(4)

и привести его к каноническому виду. Решение.

1. Определяем коэффициенты уравнения a11, a12 и a22 .

Имеем

a11 =1, a12 = −2, a22 = −21. 2. Вычислим выражение

а122 − a11a22 = 4 + 21 = 25 > 0.

3.Поскольку a122 − a11a22 > 0 при всех x, y, уравнение (4) является уравнением гиперболического типа во всей плоскости XOY.

4.Находим общие интегралы уравнения характеристик:

(dy)2 + 4dydx − 21(dx)2 = 0.

Решая это уравнение относительно dy , получаем dy = 3dx иdy = -7dx.

Следовательно, уравнение характеристик (5) имеет два вида интеграла:

h1 (x, y) = y −3x и h2 (x, y) = y + 7x. 5. В уравнении (4) делаем замену переменных:

x, y → ξ = h1 (x, y) = y −3x, η = h2 (x, y) = y + 7x.

При этом по правилу дифференцирования сложной функции

ux a −3uξ + 7uη , uy a uξ +uη, uxx a 9uξξ −54uξη + 49uηη ,

uxy a −3uξξ −54uξη + 49uηη ,

uyy a uξξ + 2uξη + uηη .

В результате замены переменных уравнение (4) принимает вид

127

9uξξ −54uξη + 49uηη +12uξξ −16uξη − 28uηη − 21uξξ −
− 42uξη − 21uηη − 7uξ +14uη −3uξ −3uη		η −ξ 2
	+ 5u =	10	,

т.е. уравнение (4) приводится к каноническому виду

uξη	= −	10	uξ +	11	uη +	5	u −	1	η −ξ		2
										.
		112		112		112		112	10

Ответ. Уравнение (4) является уравнением гиперболического типа во всей плоскости XOY и имеет канонический вид

uξη	= −	10	uξ +	11	uη +	5	u −	1	η −ξ		2
										,
		112		112		112		112	10

где ξ = y −			3x и η = y +			7x.
Пример 2. Определить тип уравнения
	uxx − 2uxy + uyy				+ ux	−u y + u = xy					(6)

и привести его к каноническому виду. Решение.

1. Определяем коэффициенты уравнения a11,a12 и

a22 . Имеем

a11 =1, a12 = −1, a 22 =1. 2. Вычисляем выражение

a122 − a11a22 =1 −1 = 0.

3.Поскольку a122 − a11a22 = 0 при всехx, y, уравнение (6) является уравнением параболического типа во всей плоскости XOY

4.Находим общие интегралы уравнения характеристик:

(dy)2 + 2dydx + (dx)2 = 0.

Решая это уравнение относительно dy получаем

dy = −dx. Следовательно, уравнение характеристик (7) имеет единственный интеграл

128

h1 (x, y) = y + x.

5. В уравнении (6) делаем замену переменных: x, y a ξ = h1 (x, y) = y + x, η = y.

(В качестве η можно было бы взять и любую другую дважды дифференцируемую функцию, не выражающую-

ся черезh1 (x, y) = y + x.)

При этом по правилу дифференцирования сложной функции:

ux a uξ , u y a uξ + uη ,

uxx a uξξ , uxy a uξξ + uξη , u yy a uξξ + 2uξη + uηη .

В результате замены переменных уравнение (6) принимает вид

uξξ − 2uξξ − 2uξη + uξξ + 2uξη + uηη + uξ −uξ −uη + u = (ξ −η)η,

Т.е. уравнение (6) приводится к каноническому виду uηη = uη −u + (ξ −η)η.

Ответ. Уравнение (6) является уравнением параболического типа во всей плоскости XOY и имеет канонический вид

uηη = uη −u + (ξ −η)η,

где ξ = y + x и η = y.

Пример 3. Определить тип уравнения

uxx + 2uxy + 2u yy + 6ux + 6u y −3u = x + y 2

(8)

и привести его к каноническому виду. Решение.

1.Определяем коэффициенты уравнения a11,a12 и a22 . Имеем

a11 =1, a12 =1, a22 = 2.

2. Вычисляем выражение

a122 − a11a22 =1 − 2 = −1 < 0.

129

3.Посколькуa122 − a11a22 < 0 при всех x, y, уравнение (8) является уравнением эллиптического типа во всей плоскости XOY

4.Находим общие интегралы уравнения характеристик:

(dy)2 − 2dydx + 2(dx)2 = 0.

Решая это уравнение относительно dy , получаем dy = (1 + i)dx и dy = (1 −i)dx.

Следовательно, уравнение характеристик (9) имеет два комплексных интеграла:

f1 (x, y) = y − x −ix и f2 (x, y) = y − x + ix.

Положим h1 (x, y) = Re f2 (x, y) = y − x и

h2 (x, y) = Im f2 (x, y) = x. (В качестве h1 и h2 можно было бы взять Re f1 (x, y) и Im f1 (x, y). )

5. В уравнении (8) делаем замену переменных: x, y a ξ = h1 (x, y) = y − x, η = x.

При этом по правилу дифференцирования сложной функции

ux a −uξ + uη , uy a uξ ,

uxx a uξξ − 2uξη + uηη , uxy a uξξ + uξη , u yy a uξξ.

В результате замены переменных уравнение (8) принимает

uξξ − 2uξη + uηη + 2uξξ + 2uξη + 2uξξ + 6(−uξ + uη )+ 6uξ −

вид, −3u =η + (ξ +η)2 ,

т.е. уравнение (8) приводится к каноническому виду uξξ + uηη = −2uη + u +η + (ξ +η)2 .

Ответ. Уравнение (8) является уравнением эллиптического типа во всей плоскости XOY и имеет канонический вид uξξ + uηη = −2uη + u +η + (ξ +η)2 ,

где ξ = y − x и η = x.

130

2. Общее решение гиперболического уравнения

Постановка задачи. Найти общее решение гиперболического уравнения

uxx + 2buxy + (b2 − a2 )uyy = 0.

(1)

План решения

1.Приводим уравнение (1) к каноническому виду. Получаем

uςη	= 0,	(2)
где ξ = y − (b + a)x,	η = y − (b − a)x (задача 1)
2. Интегрируя уравнения (2) по η , получаем
uξ = C0 (ξ).		(3)

Интегрируя уравнение (3) по ξ , получаем u(ξ,η)∫ C0 (ξ)dξ + C2 (η)≡ C1(ξ)+ C2 (η).

Следовательно, общее решение уравнения (2) имеет вид u(ξ,η) = C1 (ξ)+ C2 (η), (4)

где C1 (ξ) и C2 (η)- произвольные дважды дифференцируемые функции.

3. Подставляя в (4) ξ = y − (b + a)x и η = y − (b − a)x,

получаем общее решение уравнения (1): u(x, y) = x1 (y − (b + a)x)+ C2 (y − (b − a)x).

Делаем проверку и записываем ответ.

Пример. Найти общее решение гиперболического уравнения

uxx + 4uxy −5uyy = 0.

(5)

Решение.

1. Приводим уравнение (5) к каноническому виду. Получаем

uξη = 0,

(6)

где ξ = y −5x,η = y + x.

2. Интегрируя уравнение (6) по η, получаем

131

uξ = C0 (ξ).	(7)
Интегрируя уравнение (7) по ξ , получаем
u(ξ,η)= ∫ C0 (ξ)dξ + C2 (η)≡ C1(ξ)+ C2 (η).	(8)

3 Подставляя в (8) ξ = y −5x и η = y + x, получаем об-

щее решение уравнения (5)

u(x, y) = C1 (y −5x)+ C2 (y + x).

Делаем проверку, подставляя u(x, y) в уравнение (5).

Ответ. Общее решение уравнения (5) имеет вид u(x, y) = C1 (y −5x)+ C2 (y + x).

3. Общее решение параболического уравнения

Постановка задачи. Найти общее решение параболического уравнения

uxx + 2buxy + b2u yy + aux − abu y = 0.

(1)

План решения.

1.Приводим уравнение (1) к каноническому виду. Получаем

b2uηη + abuη = 0,

(2)

где ξ = y - bx,η = y (задача 1.)

2.Чтобы найти общее решение уравнения (2), составляем соответствующее характеристическое уравнение

b2k2 + abk = 0 и находим его корни k1 = 0 и

k2 = −a / b.

Следовательно, общее решение уравнения (2) можно за-

писать в виде
u(ξ,η) = C (ξ)+ C	2	(ξ)e−aη / b ,	(3)
1	2

где C1 (ξ) и C2 (ξ)- произвольные дважды дифференцируемые функции.

132

3. Подставляя в (3) ξ = y - bx и η = y, получаем общее

решение уравнения (1):

u(x, y) = C1 (y −bx)+ C2 ( y −bx)e−ay / b .

Делаем проверку и записываем ответ.

Пример. Найти общее решение параболического уравнения

uxx − 2uxy + uyy −ux + u y = 0.

Решение.

1. Приводим уравнение (4) к каноническому виду. Получаем

uηη + uη = 0,

(5)

где ξ = y - bx,η = y .

2.Чтобы найти общее решение уравнения (5), составля-

ем соответствующее характеристическое уравнение

k 2 + k = 0 и находим его корни k1 = 0 и k2 = −1. Следовательно, общее решение уравнения (5) можно за-

писать в виде
u(ξ,η) = C	(ξ)+ C	2	(ξ)e−η ,	(6)
1		2

где C1 (ξ) и C2 (ξ)- произвольные дважды дифференцируемые функции.

3.Подставляя в (6) ξ = y - x и η = y, получаем общее

решение уравнения (4):

u(ξ,η)= C1(y − x)+ C2 (y − x)e−y .

Делаем проверку, подставляя u(x, y) в уравнение (4).

Ответ. Обще решение уравнения (4) имеет вид u(ξ,η) = C1 (y − x)+ C2 (y − x)e− y .

4. Общее решение эллиптического уравнения

Постановка задачи. Найти общее решение эллиптического уравнения

uxx + 2buxy + (b2 + a2 )u yy = 0.	(1)
133

План решения 1. Приводим уравнение (1) к каноническому виду. По-

лучаем

uξξ + uηη = 0,

(2)

где ξ = y −bx, η = ax (задача 1.)

2.Уравнение (2) означает, что u(ξ,η) является веще-

ственной (или мнимой) частью аналитической функции f (ξ +ηi). Поэтому

u(x, y) = Re f ( y −bx + axi).

Пример. Найти общее решение эллиптического уравнения

uxx + 4uxy + 5uyy = 0.

(3)

Решение.

1. Приводим уравнение (3) к каноническому виду. Получаем

uξξ + uηη = 0,

(4)

где ξ = y - 2x, η = x.

2.Уравнение (4) означает, что u(ξ,η) является вещест-

венной (или мнимой) частью аналитической функции f (ξ +ηi). Поэтому

u(x, y) = Re f (y − 2x + xi).

Ответ. Общее решение уравнения (3) имеет вид u(x, y) = Re f (y − 2x + xi),

где f (z) −произвольная аналитическая функция.

5. Уравнение Лапласа в круге

Постановка задачи. Решить краевую задачу Дирихле для

уравнения Лапласа в круге:
u = 0, 0 ≤ r < r0 ,	(1)
u \|r =r = a cos3 ϕ + b sin 3 ϕ + p cosϕ + q sinϕ + c.	(2)
0

План решения. Уравнение Лапласа (1) в полярных координатах (r,ϕ) имеет вид

134

1	∂		∂u		1 ∂2u
		r		+		= 0.	(3)
					r 2 ∂ϕ2
r ∂r			∂r

1.Находим вспомогательные решения υ в уравнения

(3)в виде

υ(r,ϕ) = R(r)Φ(ϕ),

причем | R(0)|< ∞ и Φ(ϕ) периодична с периодом 2π .

Для этого подставляем функцию υ(r,ϕ) в уравнение (3) и разделяем переменные. Получаем

d 2 Φ

dϕ2

= −

= λ = const.

R(r)

Поэтому функции

и Φ(ϕ)являются решениями свя-

занных задач:

а) Φ′′+ λΦ = 0, Φ(ϕ + 2π ) = Φ(ϕ);

б) r

′′

′

= 0,

R(0)

< ∞.

+ rR − λR

2. Решаем задачу (а).

Общее решение уравнения Φ′′+ λΦ = 0 имеет вид

Φ(ϕ) =	~	−λϕ		~	− −λϕ	.
Φ(ϕ) =	Ae		+ Be			.
Оно периодично при		λ ≥ 0		и	имеет период 2π при
λ = n2 (n = 0,1,...).

Получаем:

~	при λ = λ0 = 0,
Φ0 (ϕ) = A0	при λ = λ0 = 0,
~		λ =	λn = n	2	(n	=1,2,...).
Φn (ϕ) = An cos nϕ + B sin nϕ при		λ =	λn = n		(n	=1,2,...).
3. Решаем задачу (б) при λ = λ0			= 0 и при			λ = λn = n2
(n =1,2,...).

При λ = λ0 = 0 имеем

r 2 R′′+ rR′ = 0.

Общее решение этого уравнения есть

135

R0 (r) = C0 + D0 ln r.

Поскольку | R0 (0)|< ∞, полагаем D0 = 0.

При λ = λn = n2 имеем

r 2 R′′+ rR′− n2 R = 0.

Общее решение этого уравнения есть
			Rn	(r) = Cn r n + Dn r −n (n =1,2,...).
Поскольку \| Rn (0)\|< ∞, полагаем Dn = 0.
4. Итак, вспомогательные решения уравнения (3) имеют
вид	~
	~		= A0 ,
u0 (r,ϕ) = C0 A0			= A0 ,
u0 (r,ϕ) = Cn r		n	~	~	n	(An cos nϕ + Bn sin nϕ),
u0 (r,ϕ) = Cn r			(An cos nϕ + Bn sin nϕ)= r			(An cos nϕ + Bn sin nϕ),
	~			~
где An = Cn An ,				Bn = Cn Bn − постоянные которые предстоит
найти.
5.	Решение задачи Дирихле (1)-(2) ищем в виде
u(r,ϕ)	∞			∞
u(r,ϕ)	= ∑un	(r,ϕ) = A0 + ∑r n (An cos nϕ + Bn sin nϕ).					(4)
	n=0			n=1

Эта функция является решением уравнения (1) при любых An и Bn , при которых ряд (4) сходится и его можно дважды

дифференцировать почленно.

6. Находим коэффициенты An и Bn , при которых u(r,ϕ) удовлетворяет граничному условию (2).

Подставим условие (2) в виде

u(r0 ,ϕ) = a cos3 ϕ + bsin 3 ϕ + p cosϕ + q cosϕ + c = 136

= c + 3a4+ p cosϕ + 3b4+ q sin ϕ + a4 cos 3ϕ − a4 sin 3ϕ.

Имеем

∞

u(r0,ϕ)= A0 + ∑r0n (An cos nϕ + Bn sin nϕ) =

n=1

=c + 3a4+ p cosϕ + 3b4+ q sinϕ + a4 cos 3ϕ − a4 sin 3ϕ.

Следовательно,

A = c,

A =

, A

+ p ,

= 0,

= 0

при

4r 3

n ≥ 4,

= 0, B = −

, B

+ q , B

= 0

при

4r3

n ≥ 4.

Подставляя эти коэффициенты в формулу (4), получаем

u(r,ϕ) = c + r 3a r0 4

Замечания.

1. Задача Дирихле

	3b
+ p cosϕ +			+ q sinϕ			+
+ p cosϕ +	4		+ q sinϕ			+
	4
			r 3	a				b
	+				cos3ϕ		−		sin 3ϕ .
	+		r 3		cos3ϕ		−	4	sin 3ϕ .
			r 3	4				4
		0

u = 0, 0 ≤ r < r0 ,	(5)
u \| Lr = r0 = f (ϕ)	(6)
при любой непрерывной функции f (ϕ)с периодом 2π	ре-

шается аналогично, но в п. 6 плана решения коэффициенты An и Bn определяются по формулам Эйлера-Фурье:

Bn = π1n 2∫π f (ϕ)sin nϕ dϕ.

r0 0

2.Подставив эти выражения для A0 , An и Bn в (4), из-

меняем порядок суммирования и интегрирования. Вычисляя сумму ряда, получаем формулу Пуассона для решения задачи

(5), (6):

	1	2π	′			r 2	− r 2		′
						0
u(r,ϕ) =		∫		) 2				2
u(r,ϕ) =	2π	∫	f (ϕ	) 2		− 2r0 r cos(ϕ −ϕ′)+ r		2	dϕ .
	2π	0			r0	− 2r0 r cos(ϕ −ϕ′)+ r

3. Смысл формулы (4) можно пояснить следующим образом. При каждом фиксированном r функцию u(r,ϕ)можно разложить в тригонометрический ряд Фурье:

∞

u(r,ϕ) = a0 + ∑an cos nϕ + bn sin nϕ.

n=1

137

138

Коэффициенты a0 , a1 ,...и b1 ,b2 ,... зависят от r . Поэтому

∞
u(r,ϕ) = a0 (r)+ ∑an (r)cos nϕ + bn (r)sin nϕ.	(7)
n=1

Подставляя эту функцию в уравнение (3), убеждаемся, что

уравнение (3) обращается в тождество, только если an (r) и
bn (r)	являются		решениями		задачи				(б)		при
λ = n2	(n = 0,1,2,...). Следовательно,			a	0	(r) = A ,		a	n	(r) = A r n
и b (r) = B					0		0		n		n
и b (r) = B		r n . При таких коэффициентах формула (7) совпа-
n	n
дает с (4).
4.	Общее решение уравнения Лапласа						u = 0 в круге
0 ≤ r < r0 имеет вид			u(x, y) = Re f (z), где					z = x + iy			и

f (z)−произвольная функция, аналитическая в круге | z |< r0 (см. задачу 4). Функцию f (z) можно представить степенным рядом:

∞

f (z) = ∑cn z n ,

n=0

Сходящимся в круге| z |< r0. . Положим x = reiϕ . Тогда

u(x, y) = Re f (z)Re ∑∞ cn r n eiϕn = ∑∞ Re[cn r n (cos nϕ + i sin nϕ)].

n=0 n=0

Последний ряд совпадает с (4), где A0 = Re c0 , An = Re cn и

Bn = −Imc0 .

Пример. Решить краевую задачу Дирихле для уравнения Лапласа в круге:

139

u = 0, 0 ≤ r < r0 ,	(8)
u \|r =1 = sin3 ϕ.	(9)

Решение. Уравнение Лапласа (1) в полярных координатах (r,ϕ) имеет вид (3)

1.Находим вспомогательные решения υ уравнения (3)

ввиде

υ(r,ϕ)= R(r)Φ(ϕ),

причем | R(0)|< ∞ и Φ(ϕ) периодична с периодом 2π.

Для этого подставляем функцию u(r,ϕ) в уравнение (3) и разделяем переменные. Получаем

	d		dR		d 2 Φ
f		f
f		f			dϕ2
	dr		dr	= −	dϕ2	= λ = const.
		R		= −		= λ = const.
		R			Φ

Поэтому функции R(r) и Φ(ϕ) являются решениями свя-

занных задач:

а) Φ′′+ λΦ = 0, Φ(ϕ + 2π ) = Φ(ϕ);

б) r 2 R′′+ rR′− λR = 0, | R(0)< ∞.

2. Решаем задачу (а).

Общее решение уравнения Φ′′+ λΦ = 0 имеет вид

~	−λ ϕ	~	− −λ ϕ	.
Φ(ϕ)= Ae		+ Be		.

140

Оно периодично		λ ≥ 0	при и	имеет период			2π при
λ = n2 (n = 0,1,...).
Получаем:
~	при	λ = λ0	= 0,
Φ0 (ϕ) = A0	при	λ = λ0	= 0,
~		~			2	(n	=1,2,...).
Φn (ϕ) = An	cos nϕ + Bn sin nϕ при λ = λn = n					(n	=1,2,...).
3. Решаем задачу (б) при λ = λ0				= 0 и при λ = λn = n2 .
При λ = λ0	= 0 имеем

r 2 R′′+ rR′ = 0.

Общее решение этого уравнения есть

R0 (r) = C0 + D0 ln r.

Поскольку | R0 (0)|< ∞, полагаем Dn = 0.

При λ = λn = n2 имеем

r 2 R′′+ rR′− n2 R = 0.

Общее решение этого уравнения есть

Rn (r) = Cn r n + Dn r −n (n =1,2,...).

Поскольку | Rn (0)|< ∞, полагаем Dn = 0.

4. Итак, вспомогательные решения уравнения (5) имеют

вид

141

	~			= A0	,
υ0 (r,ϕ) = C0 A0
υ0 (r,ϕ) = Cn r		n		~	~	n	(An cos nϕ + Bn sin nϕ),
			(An cos nϕ + Bn sin nϕ)= r
где	~		,	Bn	~
	An = Cn An				= Cn Bn − постоянные, которые предстоит

найти.

5.Решение задачи Дирихле (8)-(9) ищем в виде

∞	∞
u(r,ϕ) = ∑υn (r,ϕ) = A0 + ∑r n (An cos nϕ + Bn sin nϕ).		(10)
n=0	n=1
Эта функция является	решение уравнения (8) при	An и

Bn любых и при которых ряд (10) сходится и его можно дважды дифференцировать почленно.

6. Находим коэффициенты An и Bn при которых удовлетворяет граничному условию (9).

Представим условие (9) в виде

u(1,ϕ) = sin3 ϕ = 34 sinϕ − 14 sin 3ϕ.

Имеем

∞	3		1
u(1,ϕ) = A0 + ∑An cos nϕ + Bn sin nϕ =		sinϕ −		sin 3ϕ.
	4		4
n=0

Следовательно,

A0 = 0, An = 0 (n =1,2,...), 142

B1 = 34 , B2 = 0, B3 = − 14 , Bn = 0 при n ≥ 4.

Подставляя эти коэффициенты в формулу (10), получаем

u(r,ϕ) =

sinϕ −

r 3

sin 3ϕ.

Ответ. u(r,ϕ) =

sinϕ −

r 3

sin 3ϕ.

6. Уравнение Лапласа в цилиндре

Постановка задачи. Решить краевую задачу Дирихле для

уравнения Лапласа в цилиндре:

u = 0, 0 ≤ r < r0 , 0 < z < zo ,

(1)

u |

z=0

= r 2 − r 2 ,

0 ≤ r < r ,

(2)

u |z=z0

= 0,

0 ≤ r < r0 ,

(3)

u |r =r

= 0,

0 < z < z0 ,

(4)

План решения. Уравнение Лапласа (1) в цилиндрических

координатах (r,ϕ,z) имеет вид

∂2u

1 ∂u

1 ∂2u

∂2u

= 0.

(5)

∂r 2

r ∂r

2 ∂ϕ2

∂z 2

143

Так как граничные u |r =r0 значения функции u не зависят от ϕ и коэффициенты уравнения (5) не завися ϕ, от решение

задачи Дирихле (1)-(4) также не зависит от и его можно искать в виде

u(r,ϕ, z) ≡ u(r, z),

где функция u(r, z) удовлетворяет					уравнению	(5) с
∂2u / ∂ϕ2 ≡ 0 :
∂2u	+	1 ∂u	+	∂2u	= 0.	(6)
∂r 2				∂z 2
		r ∂r
		r ∂r

1.Находим вспомогательные решения v(r, z) уравне-

ния (6) в виде

υ(r, z) = R(r)Z (z),

причем | R(0)|< ∞, R(r0 ) = 0 и

Z (z0 ) = 0.

Для этого подставляем функцию υ(r, z) = R(r)Z(z) в урав-

нение (6) и разделяем переменные. Получаем

d 2 Z

dz 2

= −

= λ = const.

Поэтому функции R(r) и Φ(ϕ)

являются решениями свя-

занных задач:

а) R′′+

R′+ λR = 0, 0 ≤ r < r0 , | R(0)|< ∞, R(r0 ) = 0.

б) Z ′′− λZ = 0, Z (z0 ) = 0.

2. Решаем задачу (а).

Общее решение уравнения

R′′+

R′+ λR = 0 имеет вид

R(r)=

AJ0 (

λr)+ BY0 ( λr),

где J0 и Y0

− функции Бесселя и Неймана. Поскольку

| R(0)|< ∞,

а Y0 (r)→ ∞ при r → 0, полагаем B = 0.

144

Используя граничное условие R(r0 ) = 0, получаем

λn

Rn = An J0

, n =1,2,...,

где

μn

− нули функции Бесселя J0 (x),

т.е.

J0 (μn ) = 0,

n =1,2,....

= (μ

/ r )2

Решаем задачу (б). При λ

имеем

Z ′′− μr0n 2 Z = 0.

Общее решение этого уравнения, удовлетворяющее условию Z (z0 ) = 0, есть

Zn (z) = Bn sh μr0n (z0 − z).

4. Итак, вспомогательные решения уравнения (6) имеют вид

~	μn		μn	(z0 − z)=
~	μn		μn
vn (r, z)= An Bn J0	r	r sh	r
	0		0

(z0 − z),

= An J

r sh r

где

An = An Bn − постоянные, которые предстоит найти.

5. Решение u(r, z) задачи Дирихле (1)-(4) ищем в виде

∞

(z0

− z).

(7)

u(r, z) = ∑υn (r, z) = ∑An J 0

r sh

n=0

n=1

Эта функция является решением уравнения (1) и удовлетворяет граничным условиям (3), (4) при любых An при которых

ряд (7) сходится и его можно дважды дифференцировать почленно.

145

6. Находим коэффициенты An при которых u(r, z) удовлетворяет граничному условию (2):

u(r,0)

∞

= ∑An sh

z0 J0

r = r0 − r

n=1

Следовательно, по формулам Эйлера-Фурье имеем

2∫(r0

− r

rdr

(μn )

μn

4r0 J 2

2 J 2 (μ

)

μ2 J

(μ

)

An sh

n =1,2,...

Поэтому

2 J

(μ

)

n =1,2,...

μn

1 (μn )sh

Подставляя эти коэффициенты в формулу (7), получаем

∞

u(r, z) = ∑

4r0 J 2 (μn )

μn

(z0

− z).

r sh

n=1

μn

(μn )sh

Замечания.

1. Задача Дирихле

u = 0, 0 ≤ r < r0 , 0 < z < zo ,

u |z=0 = f (r),

0 ≤ r < r0 ,

u |z=z0 = 0,

0 ≤ r < r0 ,

u |r =r = 0,

0 < z < z0 ,

при произвольной непрерывной функции f(r), для которой f(r0)=0, решается аналогично.

2. Смысл формулы (7) можно пояснить следующим образом.

146

При каждом фиксированном	z функцию u(r,ϕ) можно
разложить в ряд Фурье по системе функций J0 (μn r / r0 )
(n =1,2,...):
∞				r
		μn


u(r, z) = ∑an J0				r0	.
n=1
Коэффициенты a1 , a2 ,... зависят от z.		Поэтому
∞		r
	μn				(8)

u(r, z) = ∑an (z)J 0			.
n=1		r0

Подставляя эту функцию в уравнение (6), убеждаемся, что уравнение (6) обращается в тождество, только если an (z)яв-

ляются решениями задачи (б) при λ =						(μ	n	/ r )2	(n =1,2,...).
							n	0
Следовательно, а	n	(z) = A sh μn (z		0	− z).	При таких коэффи-
	n	n	r0	0
			r0

циентах формула (8) совпадает с (7).

Пример. Решить краевую задачу Дирихле для уравнения Лапласа в цилиндре

u = 0, 0 ≤ r <1 , 0 < z <1,			(9)
u \|	=1 − r 2 ,	0 ≤ r <1,	(10)
z=0
u \|z=1	= 0,	0 ≤ r <1,	(11)
0
u \|r =1 = 0,		0 < z <1,	(12)

Решение. Уравнение Лапласа (9) в цилиндрических координатах (r,ϕ, z) имеет вид (5).

Так как граничные значения u |r=1 функции u не зависят от ϕ и коэффициенты уравнения (5) не зависят от ϕ, решение задачи Дирихле (5), (10)-(12) также не зависит от ϕ и его

можно искать в виде

u(r,ϕ, z)≡ u(r, z),

где функция u(r, z) удовлетворяет уравнению (6).

147

1. Находим вспомогательные решения уравнения (6) в виде

υ(r, z) = R(r)Z (z),

причем | R(0)|< ∞, R(1) = 0 и Z (1) = 0.

Для этого подставляем функцию v(r, z)= R(r)Z(z) в уравнение (6) и разделяем переменные. Получаем

d 2 Z

= −

dz 2

= λ = const.

Поэтому функции R(r) и Φ(ϕ)

являются решениями свя-

занных задач:

а) R′′+

R′+ λR = 0,

0 ≤ r

<1,

R(0)

< ∞, R(1) = 0.

б) Z ′′− λZ = 0, Z (1) = 0.

Решаем задачу (а).

Общее решение уравнения

R′′+

R′+ λR = 0 имеет вид

R(r)= AJ0 (

λr)+ BY0 ( λr),

где

J0 и

Y0 − функция

Бесселя

и Неймана. Поскольку

| R(0)|< ∞,

а Y0 (r)→ ∞ при r → 0,

полагаем B = 0 .

Используя граничное условие R(r0 ) = 0, получаем

n =1,2,...,

λn = μn

Rn = An J0 (μn r),

где μn −нули функции Бесселя J0 (x), т.е. J0 (μn ) = 0,

n=1,2,...

3.Решаем задачу (б). При λn = μn2 имеем

Z ′′− μn2 Z = 0.

Общее решение этого уравнения, удовлетворяющее условию Z (1) = 0, есть

Zn = Bn shμn (1 − z).

148

4.Итак, вспомогательные решения уравнения (6) имеют

вид

	~	(μnr)shμn (1 − z)= An J0 (μnr)shμn (1 − z),
	υn (r, z)= An Bn J0	(μnr)shμn (1 − z)= An J0 (μnr)shμn (1 − z),
где	~
где	An = An Bn − постоянные, которые предстоит найти.
	5. Решение u(r, z) задачи Дирихле (9)-(12) ищем в виде
	∞	∞
	un (r, z) = ∑υn	(r, z) = ∑An J0 (μn r)shμn (1 − z).	(13)
	n=1	n=1
	Эта функция является решением уравнения (5) и удовле-
творяет граничным условиям (11), (12) при любых			An , при

которых ряд (13) сходится и его можно дважды дифференцировать почленно.

Находим

коэффициенты,

An , при которых u(r, z)

удовлетворяет граничному условию (10):

∞

(μn r)shμn =1 − r 2 .

u(r,0) = ∑An J0

n=1

Следовательно, по формулам Эйлера-Фурье имеем

A shμ

2∫01 (1 − r 2 )J0 (μn r)rdr

4J 2 (μn )

, n =1,2,...

J12 (μn )

μn2 J12 (μn )

Поэтому

2J 2 (μn )

n =1,2,...

μn2 J12 (μn )shμn

Подставляя эти коэффициенты в формулу (13), получаем

∞

4J2 (μn )

J0 (μnr)shμn (1 − z).

u(r, z) = ∑

2 2

n=1

μn

J1 (μn )shμn

∞

4J2 (μn )

(μnr)shμn (1 − z).

Ответ. u(r, z) = ∑

n=1

μn

(μn )shμn

149

7. Уравнение Лапласа в шаре

Постановка задачи. Решить краевую задачу Дирихле для

уравнения Лапласа в шаре:

u = 0,

0 ≤ r < r0,

(1)

u |r =r

= a + b cosϑ + c cos2 ϑ.

(2)

План решения.

Уравнение Лапласа (1) в сферических ко-

ординатах (r,ϕ,ϑ)

имеет вид

∂

2 ∂u

∂2u

r2 sin2

∂ϕ2

∂r

(3)

∂

∂u

sinϑ

= 0.

r2 sinϑ

∂ϑ

Так как граничные значения u |r =r функции u

не зависят от

ϕ и коэффициенты уравнения (3) не зависят от ϕ решение

задачи Дирихле (1)-(2) также не зависит от ϕ и его можно

искать в виде

u(r,ϕ,ϑ) ≡ u(r,ϑ),

u(r,ϑ)

где

функция

удовлетворяет уравнению

(3) с

∂2u / ∂ϕ2 ≡ 0 :

∂

∂u

∂

∂u

sinϑ

= 0.

(4)

r 2

r 2 sinϑ

∂r

∂ϑ

Находим вспомогательные решения υ(r,ϑ)

уравне-

ния (4) в виде

υ(r,ϑ) = R(r)Θ(ϑ),

Причем | R(0)|< ∞,

| Θ(0)|< ∞, | Θ(π )|< ∞.

Для этого подставляем функцию υ(r,ϑ) в уравнение (4) и

разделяем переменные. Получаем

′′

2rR

′

′′

′

+ ctgϑ Θ = λ = const.

150

Поэтому функции R(r) и Θ(ϑ) являются решениями связан-

ных задач:					\| Θ(π )\|< ∞;
а) Θ′′ + ctgϑΘ′+ λΘ = 0, \| Θ(0)\|< ∞,
б) r 2 R′′+ 2rR′− λR = 0, \| R(0)\|< ∞.
2. Решаем задачу (а).
Уравнение			Θ′′+ ctgϑΘ′+ λΘ = 0		заменой переменной
cosϑ = z преобразуется в уравнение Лежандра
(1 − z	2		′′	′
		)Θ − 2zΘ + v(v +1)Θ = 0 , v(v +1)= λ.
Его общее решение имеет вид
			Θ(z) = CPv (z)+ DQv (z),
где Pv (z) и Qv (z)− функции Лежандра первого и второго
рода нулевого порядка				(Pv (z) ≡ Pv(0) (z) и Qv (z) ≡ Qv(0) (z)). Оно
ограничено на			[−1,1] только при v = n (n = 0,1,...), т.е. при

λ= n(n +1) и D = 0.

3.Решаем задачу (б). При λ = n(n +1) имеем

r 2 R′′+ 2rR′− n(n +1)R = 0.

Общее решение этого уравнения есть

~	n	~		−n−1	.
Rn (r) = An r		+ Bn r			.
		~	= 0.
Поскольку \| Rn (0)\|< ∞, полагаем Bn			= 0.

4. Итак, вспомогательные решения уравнения (4) имеют вид

	~	n	Pn (cosϑ) = An r	n	Pn (cosϑ),	n = 0,1,2,...,
	υn (r,ϑ) = Cn An r		Pn (cosϑ) = An r		Pn (cosϑ),	n = 0,1,2,...,
где	~
где	An = Cn An − постоянные, которые предстоит найти.
	5. Решение задачи Дирихле (1)-(2) ищем в виде
	∞		∞
	u(r,ϑ) = ∑υn (r,ϑ) = ∑An r n Pn (cosϑ).					(5)
	n=0		n=0

Эта функция является решением уравнения (1) при любых An , при которых ряд (5) сходится и его можно дважды диф-

ференцировать почленно.

6.Находим коэффициенты An , при которых u(r,ϑ)

удовлетворяет граничному условию (2):

∞

u(r0 ,ϑ) = ∑An r0n Pn (cosϑ) = a + b cosϑ + c cos2 ϑ.

n=0

Разложим функцию a + bx + cx2 в ряд по многочленам Лежандра:

	2		2c			(x)+ bP (x)+	2	cP (x)
a + bx + cx		= a +		P
			3				3
					0	1		2

Следовательно,

∞

∑An r0

Pn (cosϑ) =

a +

c P0 (cosϑ)+ bP1 (cosϑ)+

cP2 (cosϑ).

n=0

Отсюда

= a +

A =

, A

= 0 при n ≥ 3.

3r 2

Подставляя эти коэффициенты и выражения для Pn (cosϑ)

P (cosϑ) =1, P (cosϑ) = cosϑ, P (cosϑ) =

cos2

ϑ −

в (5), получаем

u(r,ϑ) = a +

c + b

cosϑ +

r 2

(3cos2 ϑ −1).

(6)

3 r 2

Замечания.

Задача Дирихле

u = 0,

0 ≤ r < r0,

(7)

u |r =r

= f (ϕ,ϑ)

(8)

f (ϕ,ϑ), периодич-

при произвольной непрерывной функции

ной по ϕ с периодом решается аналогично, но вместо много-

членов Лежандра используются сферические гармоники (шаровые функции Лапласа):

Y	(ϕ,ϑ) = P(\|m\|) (cosϑ)eimϕ	(m = 0,±1,±2,..., n = 0,1,2,...).
mn	n
		152

151

Здесь Pn(m) (cosϑ)− присоединенная функция Лежандра по-

рядка m.

Решение задачи (7)-(8) ищем в виде ряда:

∞ ∞
u(r,ϕ,ϑ)= ∑ ∑Cm n rn Ym n (ϕ,ϑ),		(9)
m=−∞ n=	0

Где коэффициенты Cm n определяются по формулам ЭйлераФурье:

	1 (2n +1)(n− \| m \|)!2ππ
Cm n =		2π(n+ \| m \|)!	∫∫ f (ϕ,ϑ)Y (ϕ,ϑ)* sinϑ dϑdϕ.
	r2
0			0 0

2.Подставив эти выражения для Cm n в (9), изменяем

порядок суммирования и интегрирования. Вычисляя сумму ряда, получаем формулу Пуассона для решения задачи (7)- (8):

u(r,ϕ,ϑ) =	1	2ππ	)	r 2 − r 2	2	3 / 2	sinϑ dϑ dϕ ,
		∫∫ f (ϕ ,ϑ		2
		′ ′		0			′ ′ ′
	4π			(r0 − 2r0 r cosγ + r		)
		0 0

где cosγ = cosϑ cosϑ′+ sinϑsinϑ′cos(ϕ −ϕ′).

3. Смысл формулы (6) можно пояснить следующим образом. При каждом фиксированном r функцию u(r,ϑ)можно

разложить в ряд Фурье по системе	функций
Pn (cosϑ) (n = 0,1,2,...):
∞
u(r,ϑ) = ∑an Pn (cosϑ).
n=0
Коэффициенты a0, a1, a2,... зависят от r. Поэтому
∞
u(r,ϑ) = ∑an (r)(cosϑ).	(10)
n=0

Подставляя эту функцию в уравнение (4), убеждаемся, что уравнение (4) обращается в тождество, только если an (r) яв-

ляются решениями задачи (б) при λ = n(n +1) (n = 0,1,2,...). 153

Следовательно,	a	n	(r) = A r n . При таких коэффициентах
		n	n

формула (10) совпадает с (6).

Пример. Решить краевую задачу Дирихле для уравнения

Лапласа в шаре:
u = 0, 0 ≤ r <1,	(11)
u \|r=1 = 3cos2 ϑ.	(12)
Решение. Уравнение Лапласа в сферических координатах
(r,ϕ,ϑ) имеет вид (3).
Так как граничные значения u \|r=r функции не зависят от
0
ϕ и коэффициенты уравнения (3) не зависят от ϕ,	решение

задачи Дирихле (11)-(12) также не зависит от ϕ и его можно

искать в виде

u(r,ϕ,ϑ) ≡ u(r,ϑ),

где функция u(r,ϑ) удовлетворяет уравнению (4).

1.Находим вспомогательные решения v(r,ϑ) уравнения

(4)в виде

υ(r,ϑ) = R(r)Θ(ϑ),

причем | R(0)|< ∞, | Θ(0)|< ∞, | Θ(π )|< ∞.

Для этой цели подставляем функцию υ(r,ϑ) в уравнение

(4) и разделяем переменные. Получаем


	r 2 R′′+ 2rR′	= − Θ′′+ ctgϑΘ′ = λ = const.

	R		Θ
Поэтому функции R(r)			и Θ(ϑ) являются решениями свя-
занных задач:			\| Θ(0)\|< ∞, \| Θ(π )\|< ∞;
а) Θ′′ + ctgϑΘ′+ λΘ = 0,

б) r 2 R′′+ 2rR′− λR = 0, | R(0)|< ∞.

2.Решаем задачу (а). Получаем

λ= n(n +1), Θn (ϑ) = Cn Pn (cosϑ), n = 0,1,2,...,

где Pn (x)− многочлены Лежандра.

154

	3. Решаем задачу (б). При λ = n(n +1)							имеем
	r 2 R′′+ 2rR′− n(n +1)R = 0.
Общее решение этого уравнения есть
	Rn (r)		~		n	~	−n−1	.
	Rn (r)	= An r				+ Bn r		.
Поскольку \| Rn (0)\|< ∞, полагаем						~
Поскольку \| Rn (0)\|< ∞, полагаем						Bn = 0.
	4 Итак, вспомогательные решения уравнения (4) имеют
вид
	~	n	Pn	(cosϑ) = An r				n	Pn (cosϑ),
	un (r,ϑ) = Cn An r		Pn	(cosϑ) = An r					Pn (cosϑ),
где	~
где	An = Cn An − постоянные, которые предстоит найти.
	5 Решение задачи Дирихле (11)-(12) ищем в виде
	∞				∞
	u(r,ϑ) = ∑υ(r,ϑ) = ∑An r n Pn (cosϑ).									(13)
	n=0			n=0

Эта функция является решением уравнения (11) при любых An , при которых ряд (13) сходится и его можно дважды диф-

ференцировать почленно.

6. Находим коэффициенты An , при которых u(r,ϑ)

удовлетворяет граничному условию (12):

∞

u(1,ϑ) = ∑An Pn (cosϑ) = 3cos2 ϑ.

n=0

Поскольку 3cos2 ϑ = P0 (cosϑ)+ 2P2 (cosϑ), имеем

∞

u(1,ϑ) = ∑An Pn (cosϑ) = P0 (cosϑ)+ 2P2 (cosϑ).

n=0

Следовательно, A0 =1, A1 = 0, A2 = 2, An = 0 при n ≥ 3. Подставляя эти коэффициенты и выражения для Pn (cosϑ)

P0 (cosϑ) =1, P2 (cosϑ) = 32 cos2 ϑ − 12 , в (13), получаем u(r,ϑ) =1 + r 2 (3cos2 ϑ −1).

Ответ. u(r,ϑ) =1 + r 2 (3cos2 ϑ −1).

155

8. Уравнение Гельмгольца в круге

Постановка задачи. Решить краевую задачу Дирихле для

уравнения Гельмгольца в круге:		(kr ) ≠ 0, n = 0,1,...,
u + k 2u = 0, 0 ≤ r < r , J	n	(kr ) ≠ 0, n = 0,1,...,	(1)
0	n	0
u \|r =r = a cos3 ϕ + b sin 3 ϕ + p cosϕ + q sinϕ + c.			(2)
0

План решения. Задача решается аналогично задаче Дирихле для уравнения Лапласа в круге (задача 5).

Уравнение Гельмгольца (1) в полярных координатах (r,ϕ)имеет вид

1 ∂

∂u

1 ∂

+ k

u = 0.

(3)

∂r

r2 ∂ϕ2

r ∂r

1. Находим вспомогательные решения v уравнения (3) в

виде

υ(r,ϕ) = R(r)Φ(ϕ),

причем | R(0)|< ∞ и Φ(ϕ)

периодична с периодом 2π

Для этого подставляем функцию υ(r,ϕ) в уравнение (3) и

разделяем переменные. Получаем

d 2 Φ

+ k

dϕ2

= −

= λ = const.

Поэтому функциии R(r) и Φ(φ) являются решениями связанных задач:

а) Φ′′+ λΦ = 0, Φ(ϕ + 2π ) = Φ(ϕ);

б) r 2 R′′+ rR′+ (k 2 r 2 − λ)R = 0, | R(0)|< ∞.

2. Решаем задачу (а).

Общее решение уравнения Φ′′+ λΦ = 0 имеет вид

~	−λϕ	~	− −λϕ	.
Φ(ϕ) = Ae		+ Be		.

156

Оно периодично	при λ ≥ 0 и имеет период 2π при
λ = n2 (n = 0,1,...).
Получаем:
~		= 0,
Φ0 (ϕ) = A0 при λ = λ0		= 0,
~	~	sin nϕ при λ = λn	= n	2	(n =1,2,...).
Φn (ϕ) = An cos nϕ + Bn		sin nϕ при λ = λn	= n		(n =1,2,...).
3. Решаем задачу (б) при λ = λn = n2			(n = 0,1,2,...). Имеем
r 2 R′′+ rR′+ (k 2 r 2 − n2 )R = 0.

Общее решение этого уравнения есть

Rn (r) = Cn J n (kr)+ DnYn (kr) (n = 0,1,2,...),

где J n и Yn − функции Бесселя и Неймана.

Поскольку | Rn (0)|< ∞, а Yn (r)→ ∞ при r → ∞, полагаем

Dn = 0.

4. Итак, вспомогательные решения уравнения (3) имеют вид

( ϕ)= ( )(~ ϕ + ~ ϕ)= vn r, Cn Jn kr An cos n Bn sin n

= J n (kr)(An cos nϕ + Bn sin nϕ).

где	~	~
где	An = Cn An ,	Bn = Cn Bn − постоянные, которые предстоит

найти.

157

5. Решение задачи Дирихле (1)-(2) ищем в виде

∞		∞
u(r,ϕ)= ∑υn (r,ϕ)= ∑Jn (kr)(An cos nϕ + Bn sin nϕ).				(4)
n=	0	n=	0

Эта функция является решением уравнения (1) при любых An и Bn , при которых ряд (4) сходится и его можно дважды

дифференцировать почленно.

6 Находим коэффициенты An и Bn , при которых u(r,ϕ) удовлетворяет граничному условию (2).

Представим условие (2) в виде

u(r0 ,ϕ) = a cos3 ϕ + bsin 3 ϕ + p cosϕ + q cosϕ + c =

= c + 3a4+ p cosϕ + 3b4+ q sinϕ + a4 cos3ϕ − a4 sin 3ϕ.

Имеем

∞

u(r0 ,ϕ) = A0 J0 (kr0 )+ ∑J n (kr0 )(An cos nϕ + Bn sin nϕ) =

n=1

=c + 3a4+ p cosϕ + a4 cos3ϕ + 3b4+ q sinϕ − a4 sin 3ϕ

Следовательно,

				c		A				1		3a							a
A	=				,		=							+ p ,	A = 0,	A =				,
A	=	J		(kr )	,		=	J		(kr			4	+ p ,	A = 0,	A =	4J		(kr )	,
0		J	0	(kr )		1		J	1	(kr	)		4		2	3	4J	3	(kr )
			0	0					1	0								3	0

An = 0 при n ≥ 4,

158

+ q ,

= 0,

= −

(kr

(kr )

)

Bn = 0 при n ≥ 4.

Подставляя эти коэффициенты в формулу (4), получаем

u(r,ϕ) = c

(kr)

(kr) 3a

+ p cosϕ +

+ q sinϕ

(kr )

(jr

) 4

(kr) a

cos 3ϕ −

sin 3ϕ .

(kr0 )

Замечания.
1. Задача Дирихле
u + k 2u = 0, 0 ≤ r < r	, J	n	(kr ) ≠ n,	n = 0,1,2...,	(5)
0		n	0
u \|r =r	= f (ϕ)				(6)
0

при любой непрерывной функции с периодом решается аналогично, но в п. 6 плана решения коэффициенты An и Bn ,

определяются по формулам Эйлера-Фурье:

A0 = 2πJ 01(kr0 )2∫0π f (ϕ)dϕ, An = πJ n1(kr0 )2∫0π f (ϕ)cos nϕdϕ,

Bn = πJ n1(kr0 )2∫0π f (ϕ)sin nϕdϕ.

159

2.Смысл формулы (4) можно пояснить следующим образом.

При каждом фиксированном r функцию u(r,ϕ) можно разложить в тригонометрический ряд Фурье:

	u(r,ϕ)		∞
	u(r,ϕ)	= a0	+ ∑an cos nϕ + bn sin nϕ.
			n=1
Коэффициенты a0 , a1 ,...и b1 ,b2 ,... зависят от							r . Поэтому
			∞				(r)sin nϕ.
	u(r,ϕ) = a0 (r)+ ∑an (r)cos nϕ + bn						(r)sin nϕ.				(7)
			n=1
	Подставляя эту функцию в уравнение (3), убеждаемся,
что уравнение (3) обращается в тождество, только если an (r)
и	bn (r) являются		решениями	задачи				(б)			при
λ = n2 (n = 0,1,2,...).		Следовательно,		a	n	(r) = A J			n	(kr)	и
					n		n		n
bn (r) = Bn J n (kr). При таких коэффициентах формула (7) сов-
падает с (4).
	Пример. Решить краевую задачу Дирихле для уравнения
Гельмгольца в круге:
		u + 4u = 0, 0 ≤ r <1,									(8)
			u \|r=1 = sin3 ϕ.								(9)

Решение. Уравнение Гельмгольца (1) в полярных координатах (r,ϕ) имеет вид (3) с k 2 = 4.

1. Находим вспомогательные решенияуравнения (3) в виде

160

υ(r,ϕ) = R(r)Φ(ϕ),

причем | R(0)|< ∞ и Φ(ϕ) периодична с периодом 2π

Для этого подставляем функцию υ(r,ϕ) в уравнение (3) и разделяем переменные. Получаем

d 2 Φ

+ 4r

dϕ2

= −

= λ = const.

Поэтому функции R(r) и Φ(ϕ) являются решениями связанных задач:

а) Φ′′+ λΦ = 0, Φ(ϕ + 2π ) = Φ(ϕ);

б) r 2 R′′+ rR′+ (4r 2 − λ)R = 0, | R(0)|< ∞.

2. Решаем задачу (а).

Общее решение уравнения Φ′′+ λΦ = 0 имеет вид

		~	−λϕ	~ − −λϕ	.
	Φ(ϕ) = Ae			+ Be	.
Оно периодично	при	λ ≥ 0		и имеет	период 2π при
λ = n2 (n = 0,1,...).
Получаем:
~		= 0,
Φ0 (ϕ) = A0 при λ = λ0		= 0,
~	~					2	(n =1,2,...).
Φn (ϕ) = An cos nϕ + Bn sin nϕ при λ = λn = n							(n =1,2,...).
		161

3. Решаем задачу (б) при λ = λn = n2 (n =1,2,...). Имеем

r 2 R′′+ rR′+ (4r 2 − n2 )R = 0.

Общее решение этого уравнения есть

Rn (r) = Cn J n (2r)+ DnYn (2r) (n = 0,1,2,...),

где J n и Yn − функции Бесселя и Неймана.

Поскольку | R(0)|< ∞, а Yn (r)→ ∞ при r → 0, полагаем

Dn = 0.

4. Итак, вспомогательные решения уравнения (5) имеют

вид

	~	~
υn (r,ϕ) = Cn J n (2r)(An cos nϕ + Bn sin nϕ)=
		= Jn (2r)(An cos nϕ + Bn sin nϕ),
~		~
где An = Cn An,	Bn = Cn Bn − постоянные, которые предстоит
найти.
5. Решение задачи Дирихле (8)-(9) ищем в виде
∞		∞
u(r,ϕ) = ∑υn (r,ϕ) = ∑J n (2r)(An cos nϕ + Bn sin nϕ).			(10)
n=0		n=0

Эта функция является решением уравнения при любых An и Bn , при которых ряд (10) сходится и его можно дважды дифференцировать почленно.

162

6. Находим коэффициенты An и Bn , при которых u(r,ϕ) удовлетворяет граничному условию (9).

Представим условие (9) в виде

u(1,ϕ) = sin3 ϕ = 34 sinϕ − 14 sin 3ϕ.

Имеем

∞

u(1,ϕ) = A0 J0 (2)+ ∑J n (2)(An

cos nϕ + Bn

sin nϕ) =

sin ϕ −

sin 3ϕ.

n=1

Следовательно,

= 0,

= 0 (n =1,2,...),

B =

0, B = −

= 0 при n ≥ 4.

4J1 (2)

4J3 (2)

Подставляя эти коэффициенты в формулу (10), получаем

u(r,ϕ) =

3 J1 (2r)

1 J3 (2r)

sinϕ −

sin 3ϕ.

J1 (2)

J3 (2)

u(r,ϕ) =

3 J1 (2r)

1 J3 (2r)

Ответ.

sinϕ −

sin 3ϕ.

J1 (2)

J3 (2)

9. Уравнение Гельмгольца в шаре

Постановка задачи. Решить краевую задачу Дирихле для уравнения Гельмгольца в шаре:

163

u + k 2u = 0, 0 ≤ r < r , J	n/2	(kr ) ≠ 0, n =1,3,...,	(1)
0	n/2	0
u \|r =r = a + b cosϑ + c cos2 ϑ.			(2)
0

План решения. Задача решается аналогично задаче Дирихле для уравнения Лапласа в шаре (задача 7).

Уравнение Гельмгольца (1) в сферических координатах (r,ϕ,ϑ) имеет вид

∂

∂u

∂2u

∂

∂u

sinϑ

+ (3)

r 2

r 2 sin 2 ϑ

∂ϕ2

r 2 sinϑ

∂r

∂ϑ

Так как граничные значения u |r=r

+ k 2u = 0.

функции не зависят от

ϕ и коэффициенты уравнения (3) не зависят от решение за-

дачи Дирихле (1)-(2) также не зависит от ϕ и его можно ис-

кать в виде

u(r,ϕ,ϑ) ≡ u(r,ϑ),

где функция удовлетворяет уравнению (3) с

∂2u / ∂ϕ2 ≡ 0:

∂

∂u

∂

∂u

sinϑ

+ k

u = 0 . (4)

r2 sinϑ

∂r

∂ϑ

Находим вспомогательные решения υ(r,ϑ) уравне-

ния (4)

в виде

υ(r,ϑ) = R(r)Θ(ϑ),

причем | R(0)|< ∞, | Θ(0)|< ∞,

| Θ(π )|< ∞.

Для этого подставляем функцию υ(r,ϑ) в уравнение (4) и

разделяем переменные. Получаем

r 2 R′′+ 2rR′+ k 2 r 2 R

= −

Θ′′+ ctgϑΘ′ = λ = const.

Поэтому функции R(r)

и Θ(ϑ) являются решениями связан-

ных задач:

164

n=0

а) Θ′′ + ctgϑΘ′+ λΘ = 0,

| Θ(0)|< ∞, | Θ(π )|< ∞;

б) r 2 R′′+ 2rR′+ (k 2 r 2 − λ)R = 0, | R(0)|< ∞.

2. Решаем задачу (а).

Уравнение

Θ′′+ ctgϑΘ′+ λΘ = 0

заменой

переменной

cosϑ = z преобразуется в уравнение Лежандра

(1 − z 2 )Θ′′− 2zΘ′+ v(v +1)Θ = 0 v(v +1) = λ.

Его общее решение имеет вид

Θ(z) = CPv (z)+ DQv (z),

где Pv (z) и Qv (z)−функции Лежандра первого и второго ро-

да нулевого порядка

(Pv (z) ≡ Pv(0) (z))

и Qv (z) ≡ Qv(0) (z).

Оно

ограничено на

[-1,1]

только при v = n (n = 0,1,...), т.е.

при

λ = n(n +1) и D = 0.

Решаем задачу (б). При λ = n(n +1) имеем

r2 R′′+ 2rR′+[k 2r2 − n(n +1)]R = 0.

Общее решение этого уравнения есть

(kr)

J n+1/ 2 (kr)

Yn+1/ 2

Rn (r) = An

+ Bn

где J n+1/ 2 и Yn+1/ 2 − функции Бесселя и Неймана.

Поскольку

| Rn (0)|< ∞, а Yn+1/ 2 (r)→ ∞ при r → 0,

полагаем

= 0.

4. Итак, вспомогательные решения уравнения (4) имеет

вид

J n+1/ 2 (kr)

Pn (cosϑ) =

Pn (cosϑ)

υn (r,ϑ) = Cn An

(n = 0,1,2,...), где

− постоянные, которые предстоит

An = Cn An

найти.

Решение задачи Дирихле (1)-(2) ищем в виде

∞

J n+1/ 2 (kr)

Pn (cosϑ).

u(r,ϑ) = ∑υn (r,ϑ) =

∑An

(5)

n=0

165

Эта функция является решением уравнения (1) при любых An, при которых ряд (5) сходится и его можно дважды дифференцировать почленно.

6. Находим коэффициенты An при которых u(r,ϑ)удовлетворяет граничному условию (2)

u(r0 ,ϑ) = ∑∞ An J n+1/ 2 (kr0 )Pn (cosϑ) = a + b cosϑ + c cos2 ϑ. r0

Разложим функцию в ряд по многочленам Лежандра

a + bx + cx

= a +

P (x)+ bP (x)+

(x):

Следовательно,

∞

(cosϑ) =

∑An J n+1/ 2 (kr0 )Pn

n=0

= a +

c P (cosϑ)+ bP (cosϑ)+

cP (cosϑ).

Отсюда

= b

= a

(kr )

1/ 2

3 / 2

5 / 2

= 0 при n ≥ 3.

Подставляя эти коэффициенты и выражения для Pn (cosϑ)

P (cosϑ) =1,

P (cosϑ) = cosϑ,

P (cosϑ) =

cos2 ϑ −

в (5), получаем

(kr)

r J

3 / 2

u(r,ϑ) = a

1/ 2

+ b

cosϑ +

r J1/ 2

(kr0 )

r J3 / 2 (kr0 )

c r0 J5 / 2 (kr)

(3cos

ϑ −1).

5 / 2

(kr )

Пример. Решить краевую задачу Дирихле для уравнения Гельмгольца в шаре:

166

u + 2u = 0, 0 ≤ r <1,	(6)
u \|r =1 = 3cos2 ϑ.	(7)

Решение. Уравнения Гельмгольца в сферических координатах (r,ϕ,ϑ) имеет вид (3)

Так как граничные значения u |r=1 функции не зависят от ϕ и коэффициенты уравнения (3) не зависят от ϕ решение задачи Дирихле (6)-(7) также не зависит от ϕ и его можно

искать в виде

u(r,ϕ,ϑ) ≡ u(r,ϑ),

где функция u(r,ϑ) удовлетворяет уравнению (4).

1.Находим вспомогательные решения υ(r,ϑ) уравне-

ния (4) в виде
		υ(r,ϑ) = R(r)Θ(ϑ),
причем \| R(0)\|< ∞, \| Θ(0)\|< ∞, \| Θ(π )\|< ∞.
Для этой цели подставляем функцию υ(r,ϑ) в уравнение
(4) и разделяем переменные. Получаем
		r 2 R′′+ 2rR′+ 2r 2 R		= − Θ′′+ ctgϑΘ = λ = const.

		R		Θ
Поэтому функции R(r)			и Θ(ϑ) являются решениями свя-
занных задач:				\| Θ(0)\|< ∞, \| Θ(π)\|< ∞;
а) Θ′′+ ctgϑΘ′+ λΘ = 0,
б) r 2 R′′+ 2rR′+ (k 2 r 2 −λ)R = 0, \| R(0)\|< ∞.
2.	Решаем задачу (а). Получаем
		λ = n(n +1), Θn (ϑ) = Cn Pn (cosϑ),			n = 0,1,2,...,
где Pn (x)− многочлены Лежандра.
3	Решаем задачу (б). При λ = n(n +1)				имеем

r 2 R′′+ 2rR′+[2r 2 = n(n +1)]R = 0.

Общее решение этого уравнения есть

167

	Rn (r) =	~ J n+1/ 2 ( 2r)		+ Bn	Yn+1/ 2 ( 2r)		,
	Rn (r) =	An	r	+ Bn		r	,
			r			r
где	J n+1/ 2 и Yn+1/ 2 − функции Бесселя и Неймана. Поскольку
\| Rn (0)\|< ∞, а Yn+1/ 2 (r)→ ∞ при r → 0 , полагаем							~	= 0.
\| Rn (0)\|< ∞, а Yn+1/ 2 (r)→ ∞ при r → 0 , полагаем							Bn	= 0.
	4. Итак, вспомогательные решения уравнения (4) имеет
вид						J n+1/ 2 ( 2r)
υn	~ J n+1/ 2 ( 2r)		Pn (cosϑ) =		An	J n+1/ 2 ( 2r)		Pn (cosϑ),
υn	(r,ϑ) = Cn An	r	Pn (cosϑ) =		An	r		Pn (cosϑ),
	~	r				r
	~
где An = Cn An − постоянные, которые предстоит найти.
	5. Решение задачи Дирихле (6)-(7) ищем в виде
	∞	(r,ϑ) =	∞		( 2r)Pn (cosϑ).
	u(r,ϑ) = ∑υn	(r,ϑ) =	∑An J n+1/ 2		( 2r)Pn (cosϑ).				(8)
	n=0		n=0		r

Эта функция является решением уравнения (6) при любых An , при которых ряд (8) сходится и его можно дважды диф-

ференцировать почленно.

6. Находим коэффициенты An, при которых u(r,θ) удовлетворяет граничному условию (7):

∞			(	2 )Pn (cosϑ) = 3cos2 ϑ.
u(1,ϑ) = ∑An J n+1/ 2
n=0
Поскольку	2 ϑ = P	(cosϑ)+ 2P (cosϑ),
3cos
	0			2

имеем

u(1,ϑ) = ∑∞ An J n+1/ 2 ( 2 )Pn (cosϑ) = P0 (cosϑ)+ 2P2 (cosϑ).

n=0

Следовательно, A0 =1/ J1/ 2 ( 2 ), A1 = 0, A2 = 2 / J5 / 2 ( 2 ), An = 0 при n ≥ 3.

Подставляя эти коэффициенты и выражения для Pn (cosϑ)

P0 (cosϑ) =1, P2 (cosϑ) = 23 cos2 ϑ − 12 168

в (8), получаем

u(r,ϑ) =	J1/ 2		(	2r) + J5 / 2 (				2r) (3cos2		ϑ −1).
	J1/ 2	(		2 )	r	J5 / 2	(	2 )	r
Ответ. u(r,ϑ) =	J1/ 2	(	2r)		+	J5 / 2	(	2r)	(3cos2 ϑ −1).
J1/ 2 (			2 ) r			J5 / 2 ( 2 ) r
10. Собственные функции и собственные значения
				оператора Лапласа
Постановка задачи. Найти всеλ								и u такие, что
u = λu в области Ω										(1)
αu + β	∂u = 0			на границе области Ω						(2)
	∂n

План решения.

1.Выбираем систему координат, такую, что граница области разделяется на участки, на каждом из которых одна из координат не меняется.

2.Переходим к выбранной системе координат, делая замену переменных в уравнении (1) и граничном условии (2).

3.Функции u ищем в виде произведения вспомогательных функций, каждая из которых зависит от одной координаты.

4.Используя метод разделения переменных, получаем из

(1)-(2) краевые задачи (задачи Штурма-Лиувилля) для обыкновенных дифференциальных уравнений, определяющие вспомогательные функции.

169

5. Решаем краевые задачи для вспомогательных функций и записываем ответ.

Замечание. Функции u определены с точностью до числового множителя и могут содержать произвольные посто-

янные.
Пример. Найти всеλ и u такие, что
u = λu в области Ω ={r 2 < x2		+ y2 < r 2		},	(3)
	1		2
αu + β ∂u = 0	на границе области Ω				(4)
∂n
где α =1, β = 0 при x2	+ y2 = r 2 и α = 0,		β =1 при
	1

x2 + y2 = r22 .

Решение.

1. Выбираем систему координат, такую, что граница области Ω разделяется на участки, на каждом из которых одна из координат не меняется.

В данном случае Ω − кольцо с центром в начале координат. Граница Ω состоит из двух участков x2 + y2 = r12 и x2 + y2 = r22 . На каждом из них не изменяется координата

полярной системы координат. Поэтому используем полярные координаты.

2. Переходим к полярной системе координат, делая замену переменных в уравнении (3) и граничном условии (4). Получаем

170

1 ∂

∂u

∂2u

= λu, r1

< r < r2 ,

(5)

∂ϕ2

r ∂r

∂r

u |r =r = 0,

(6)

∂u

r=r = 0,

(7)

∂r

3 Функции u(r,ϕ) ищем в виде произведения вспомога-

тельных функций, каждая из которых зависит только от одной координаты:

u(r,ϕ) = R(r)Φ(ϕ).

(8)

4 Вспомогательные функции R(r) и Φ(ϕ) определяют-

ся краевыми задачами для обыкновенных дифференциальных уравнений, которые получаются из (5)-(7) методам разделения переменных.

Подставляя (8) в (5)-(7) и разделяя переменные, получаем

1	′ ′		1 Φ′′
r	′ ′
r	(rR )	+			= λ,
				Φ
	R		r 2	Φ

R(r1 ) = 0, R′(r2 = 0).

Следовательно, имеем две краевые задачи:

(а) Φ′′− vΦ = 0, Φ(0) = Φ(2π );
(б)	′ ′	+ (v − λr	2	)R	= 0, R(r1 ) = 0,	′	(r	2	)= 0.
(б)	r(rR )	+ (v − λr		)R	= 0, R(r1 ) = 0,	R	(r		)= 0.
					171

5. Решаем краевые задачи (а) и (б).

Общее решение дифференциального уравнения

Φ′′ − vΦ = 0 имеет вид

Φ(ϕ) = C1e vϕ + C2 e− vϕ .

Условие Φ(0) = Φ(2π ) выполняется только если v = −n2 , где n = 0,±1,±2,... Поэтому задача (а) имеет бесконечное множество решений

Φn (ϕ) = C1e	inϕ	+ C2 e		−inϕ	~	~
Φn (ϕ) = C1e		+ C2 e			= An cos nϕ + Bn sin nϕ,
vn = −n2 ,
где n = 0,1,2,...,	а	~	и	~
где n = 0,1,2,...,	а	An	и	Bn − произвольные постоянные (при

n = −1,2,... получаются решения, отличающиеся от Φn толь-

ко знакомBn ).

Задача (б) при λ = 0 имеет только решение R(r) ≡ 0. При λ ≠ 0 общее решение дифференциального уравнения

задачи (б) r(rR′)′ + (v − λr 2 )R = 0 с v = −n2 имеет вид

R(r) = CJ n ( − λr)+ DYn ( − λr),

где J n и Yn функции Бесселя и Неймана, а C и D −произвольные постоянные.

Из граничных условий R(r1 ) = 0 и R′(r2 ) = 0 получаем систему уравнений для определения C и D :

172


		− λr1 )+ DYn ( − λr1 )= 0,
CJ n (							(9)
		λJ ′	( − λr	)+ D − λY ′( − λr )=
C −							0.
		n	2	n	2
Эта система имеет ненулевые решения тогда и только то-
гда, когда ее определитель равен нулю, т.е.
	J n ( − λr1 )			Yn ( − λr1 )		= 0.	(9)

	− λJ n′(		− λr2 )	− λYn′( - λr2 )

Поэтому λ доопределяется уравнением

J n ( − λr1 )Yn′( − λr2 )− J n′( − λr2 )Yn ( − λr1 )= 0.

Оно имеет бесконечное множество решений
λ = μkn2	(k =1,2,...).

Ответ. Собственные функции и собственные значения оператора Лапласа в кольце r1 < r < r2 с граничными условиями

(6)-(7) имеют вид

ukn (r,ϕ) = (Ckn J n (μkn r))(An cos nϕ + Bn sin nϕ),

λkn = −μkn2 ,
где n =1,2,..., k = 0,1,2,..., а Ckn ,		Dkn −нетривиальное реше-
ние системы (9), An и Bn	−произвольные постоянные,		не
равные нулю одновременно.
11. Уравнение Пуассона в кольце
Постановка задачи. Решить краевую задачу Дирихле для
уравнения Пуассона в кольце:
u = f (r,ϕ),	r1	< r < r2 ,	(1)
u \|r=r = g1 (ϕ),			(2)
1
173

∂u		= g2 (ϕ).	(3)

∂r
		r=r
	2

План решения. Решение краевой задачи (1)-(3) ищем в виде тригонометрического ряда Фурье:

∞
u(r,ϕ) = a0 (r)+ ∑an (r)cos nϕ + bn (r)sin nϕ,	(4)

n=1

где a0 (r), an (r),bn (r)− функции, которые предстоит найти.

1.Подставляем (4) в уравнение (1). Получаем

1 d

(r) + ∑

an (r) −

an (r) cos nϕ +

r dr

bn (r)

−

bn (r) sin nϕ

= f (r,ϕ).

r dr

2. Используя формулы Эйлера-Фурье, находим коэффициенты при 1, cos nϕ,sin nϕ :

1 d

1 2π

(r)

f (r,ϕ)dϕ = a

(r),

(5)

2π ∫0

r dr

1 d

2π

(r)

−

(r)=

f (r,ϕ)cos nϕ dϕ = a

(r),

(6)

r dr

π ∫0

1 d

2π

b (r)

−

b (r)=

f (r,ϕ)sin nϕ dϕ = b

(r).

(7)

r dr

π ∫0

3. Решаем дифференциальные уравнения (5)-(7) и находим коэффициенты a0 (r), an (r),bn (r) с точностью до произ-

вольных постоянных.

174

а) Уравнение (5) допускает понижение порядка. Общее решение этого уравнения определяется формулой

Вычисляя интегралы, получаем
a0 (r) = A0 (r)+ E0 + F0 ln r,	(8)
где A0 (r) — известная функция, а Ео и Fo — пока произволь-

ные постоянные.

б) Уравнение (6) решается методом Лагранжа вариации произвольных постоянных.

Общее решение однородного уравнения

1 d

(r)

−

(r) = 0

r dr

имеет видan (r) = Cn r n

+ Dn r −n . Поэтому общее решение не-

однородного уравнения (6) имеет вид

an (r)

= Cn (r)r n + Dn (r)r −n .

ФункцииCn (r)

(r)

определяются

системой

дифференциальных уравнений:

′

(r) = 0,

(r)+ Dn

C′

(r)+ D′

(r) = r

n+1 ~

(r)

/ n.

Следовательно,

Cn (r) =

−n ~

(r)rdr и

n ~

Dn (r)

= −

an (r)rdr.

∫

2n ∫

Поэтому

an (r)

r n

−n ~

(r)rdr −

r −n

(r)rdr.

2n ∫

∫

Вычисляя интегралы, получаем

(r) = A

(r)+ E

r n + F r −n .

(9)

где An (r) — известная функция, а

и Fn

— пока произ-

вольные постоянные.

175

в) Аналогично п. (б),

r n

−n ~

r −n

n ~

bn (r) =

∫

bn (r)rdr −

∫

r bn (r)rdr.

Вычисляя интегралы, получаем

(r) = B

(r)+ G

r n

+ H

r −n ,

(10)

гдеBn (r)— известная функция, а Gn и H n — пока произволь-

ные постоянные.

4. Используем граничные условия (2) и (3), чтобы найти постоянные E0 , F0 , En , Fn ,Gn , H n .

Граничное условие (2) с учетом (4), (8)-(10) можно представить в виде

A0 (r1 )+ E0 + F0 ln r1 + ∑∞ [(An (r1 )+ En r1n + Fn r1−n )cos nϕ +

n=1

+(Bn (r1 )+ Gn r1n + H n r1−n )sin nϕ] = g1 (ϕ).

По формулам Эйлера-Фурье получаем

(r )+ E

+ F ln r =

2π g

(ϕ)dϕ,

(11)

2π

∫0

)+ E r n + F r −n

2π g (ϕ)cos nϕdϕ,

(12)

n 1

∫

)+ G r n + H r −n

2π g (ϕ)cos nϕdϕ, .

(13)

n 1

∫

Граничное условие (3) с учетом (4), (8)-(10) можно представить в виде

	∞
A0′(r2 )+ F0 r2−1 + ∑[(An′(r2 )+ nEn r2n−1 − nFn r2−n−1 )cos nϕ +
	n=1
	+ (Bn′(r2 )+ nGnr2n−1 − nHnr2−n−1 )sin nϕ] = g2 (ϕ).
По формулам Эйлера-Фурье получаем
A′0	(r2 )+ F0r2−1 =	1	2π g2 (ϕ)dϕ,	(14)
A′0	(r2 )+ F0r2−1 =	2π	2π g2 (ϕ)dϕ,	(14)
		2π	∫0
			176

An′(r2 )+ nEn r2n−1 − Fn r2−n−1	=	1	2π g2 (ϕ)cos nϕdϕ,	(15)
An′(r2 )+ nEn r2n−1 − Fn r2−n−1	=	π	2π g2 (ϕ)cos nϕdϕ,	(15)
		π	∫
			0
Bn′(r1 )+ nGn r2n=1 − nH n r2−n−1	=	1	2π g2 (ϕ)sin nϕdϕ.	(16)
Bn′(r1 )+ nGn r2n=1 − nH n r2−n−1	=	π	2π g2 (ϕ)sin nϕdϕ.	(16)
		π	∫
			0

Постоянные E0 , F0 находим, решая систему линейных урав-

нений (11), (14):
			= −A0 (r1 )+			1	2π	g1(ϕ)dϕ,
E0	+ F0 ln r1						∫0
						2π
	−1		(r1 )+	1	2π	g2 (ϕ)dϕ.

		′			∫0

F0r2 = −A0				2π

Постоянные En , Fn находим из системы уравнений (12), (15), а постоянныеGn , H n — из системы уравнений (13), (16).

5.	Подставляем значения постоянных E0 , F0 , En , Fn ,
Gn , H n	в формулы (8)-(10), подставляем a0 (r), an (r),bn (r) из

формул (8)-(10) в (4) и записываем ответ.

Замечания.

1. Краевая задача для уравнения Лапласа в кольце решается аналогично, но проще, так как f (r,ϕ) ≡ 0.Поэтому в

формулах (8)-(10) A0 (r) ≡ 0, An (r) ≡ 0, Bn (r) ≡ 0.

2. Краевая задача для уравнения Пуассона в круге решается аналогично, но проще, так как в формулах (8)—(10) F0 = 0, Fn = 0, H n = 0 в силу условий | a0 (0)|< ∞, | an (0)|< ∞, | bn (0)|< ∞.

3. Краевая задача для уравнения Пуассона вне круга решается аналогично, но проще, так как в формулах (8)-{10) F0 = 0, Fn = 0, H n = 0 в силу условий | a0 (∞)|< ∞, | an (∞)|< ∞, | bn (∞)|< ∞.

Пример. Решить краевую задачу Дирихле для уравнения Пуассона в кольце:

177

u = r 3 cosϕ,		1 < r < 2,	(17)
u \|r=1 = cos 2ϕ,			(18)
∂u	= sin 3ϕ.		(19)

∂r
	r=2

Решение. Решение краевой задачи (17)-{19) ищем в виде тригонометрического ряда Фурье

∞
u(r,ϕ) = a0 (r)+ ∑an (r)cos nϕ + bn (r)sin nϕ ,	(20)

n=1

гдеa0 (r), an (r),bn (r)— функции, которые предстоит найти. 1. Подставляем (20) в уравнение (17). Получаем

1 d

∞

1 d

(r)

+ ∑

an (r)

−

2 an (r) cos nϕ +

r dr

n=1

r dr

bn (r)

−

bn (r) sin nϕ

= r

sinϕ.

r dr

2. Используя формулы Эйлера-Фурье, находим коэффициенты при 1, cos nϕ,sin nϕ :

1 d

1 2π

(r)

cosϕ dϕ = 0,

(21)

r dr

dr 0

2π ∫0

1 d

2π

(r)

−

(r) =

∫0

cosϕ cos nϕdϕ = a

(r), (22)

r 2

r dr

1 d

2π

(r)

−

(r) =

cosϕsin nϕdϕ = 0.

(23)

r dr

r 2

∫0

3. Решаем дифференциальные уравнения (21)-(23) и находим коэффициенты a0 (r), an (r),bn (r)с точностью до произ-

вольных постоянных.
а) Общее решение уравнения (21) имеет вид
a0 (r) = E0 + F0 ln r,	(24)

где E0 и F0 — пока произвольные постоянные. 178

б) Уравнение (22) решается методом Лагранжа вариации произвольных постоянных. Общее решение однородного уравнения

1 d

(r)

−

(r) = 0

r 2

r dr

имеет вид an (r) = Cn r n + Dn r −n . Поэтому общее решение не-

однородного уравнения (22) имеет вид

(r) = Cn (r)r n + Dn (r)r −n .

ФункцииCn (r)

(r)

определяются

системой

дифференциальных уравнений:

′

Cn (r)+ Dn (r) = 0,

′

n+1

Cn (r)+ Dn (r) = r

an (r)/ n.

Следовательно,

−n ~

Cn (r) =

∫

a(r)rdr и

Dn (r) = −

∫

an (r)rdr.

Поэтому

−n ~

r−n

n ~

an (r)=

∫

(r)rdr −

∫

r an (r)rdr.

Вычисляя интегралы, получаем

(r) =

r 5

+ E r + F r −1 ,

(25)

(r) = E

r n

+ F r −n , n ≥ 2,

где En и Fn – пока произвольные постоянные.

в) Аналогично п. (б),

(r)

= G

r n

+ H

r −n ,

(26)

где Cn и H n — пока произвольные постоянные.

4. Используем граничные условия (18) и (19), чтобы найти постоянные E0 , F0 , En , Fn ,Gn , H n .

Граничное условие (18) с учетом (20), (24)-{26) можно представить в виде

179

∞

E0 +

cosϕ + ∑(En

+ Fn )cos nϕ + (Gn

+ H n )sin nϕ = cos 2ϕ.

n=1

По формулам Эйлера-Фурье получаем

= 0,

(27)

+ E + F = 0,

+ F =1, E

+ F

= 0 при n ≥ 2,

(28)

+ H n = 0 .

(29)

Граничное условие (19) с учетом (20), (24)-(26) можно

представить в виде

∞

cosϕ +

∑[(nEn 2−n−1 − nFn 2−2−1 )cos nϕ +

n=1

+ (nGn 22−1 − nH n 2−n−1 )sin nϕ] = sin 3ϕ.

По формулам Эйлера—Фурье получаем

= 0 ,

(30)

10 + E −

= 0,

2n−1

− F 2−n−1 = 0,

(31)

Gn 2n−1 − H n 2−n−1

= 0 при n ≠ 3,

3G3 22 −3H n 2−4 =1. (32)

Постоянные E0,F0 находим, решав систему линейных

уравнений (27), (30). Очевидно, что

= 0

F0 = 0.

(33)

Постоянные En,Fn находим из системы уравнений (28), (31):

1	+ E + F = 0,			10	+ E −	F1	= 0;

24	1	1	3		1	4

E2 + F2 =1, E2 2 − F2 2−3 = 0;

En + Fn = 0, En 2n−1 − Fn 2−n−1 = 0 при n ≥ 3.

Получаем

E1 = −10740 , F1 = 3079 , E2 = 171 , F2 = 1716 , En = 0, Fn = 0 приn ≥ 3. 180

(5)

(6)

(7)

Постоянные Gn , H n находим из системы уравнений (29),

(32):

Gn + H n = 0, Gn 2n−1 − H n 2−n−1 = 0 при n ≠ 3,

Получаем

3G3 22 −3H3 2−4 =1.

G = 0,

= 0, при n ≥ 3,

G =

, H

= −

195

5. Подставляем

значения

постоянных

E0 , F0 , En , Fn ,

Gn , H n в формулы (24)-(26), подставляем a0 (r), an (r),bn (r) из

формул (24)-(26) в (20) и записываем ответ.

r 5

107

−1

−

r +

Ответ. u(r,ϕ) =

cosϕ +

−1

cos 2ϕ

−

sin 3ϕ.

195

12. Уравнение Пуассона в прямоугольнике

Постановка задачи. Решить краевую задачу для уравне-

ния Пуассона в прямоугольнике
u = f (x, y),	x (0,α), y (0, β),		(1)
u(0, y) = g1 (y),	u(α, y) = g2 (y),	y (0, β),	(2)
u y (x,0) = g3 (x),	u y (x, β) = g4 (x),	x (0,α).	(3)
План решения. Искомая функция u(х,у) может быть пред-
ставлена
u(x, y) =υ(x, y)+ w(x, y),			(4)

гдеυ(x, y)— решение краевой задачи для уравнения Пуассо-

на с однородными граничными условиями:

υ = f (x, y), x (0,α), y (0, β), υ(0, y) =υ(α, y) = 0, y (0, β),

υy (x,0) =υy (x, β) = 0, x (0,α), 181

w(x, y) — решение краевой задачи для уравнения Лапласа:

w = 0,	x (0,α), y (0, β),		(8)
w(0, y) = g1 (y),	w(α, y) = g2 (y),	y (0, β),	(9)
wy (x,0) = g3 (x),	wy (x, β) = g4 (x),	x (0,α).	(10)

1. Решение задачи (5)-(7) ищем в виде ряда по собственным функциям оператора Лапласа с граничными усло-

виями (6)-(7) (задача 10):

∞ ∞	π mx cos	π ny.
υ(x, y) = ∑∑Amn sin	π mx cos	π ny.	(11)
m=1 n=0	α	β

Эта функция удовлетворяет граничным условиям (6)-(7) при любых Amn , при которых ряд (11) сходится и его можно

дифференцировать почленно по у. Найдем коэффициенты Amn , при которых функция (11) является решением уравне-

ния (5).

Подставляя функцию (11) в уравнение (5), имеем

∞ ∞

πm 2

πn

(x, y).

−

∑∑ mn

sin

mx cos

ny = f

m 1 n

Отсюда в силу формул Эйлера-Фурье следует, что

= −

α β

f (x, y)sin

π mxdydx,

(πm /α)2 2α β

∫∫0 0

= −

α β

f (x, y)sin

π mx cos

π nydydx.

(πm /α)2 + (πn / β)2

2α 2β

∫∫0 0

Подставляя эти коэффициенты в (11), находим υ(x, y).

2. Решение задачи (8)-(10) ищем в виде

(12)

w(x, y) = w(x, y)+ w(x, y),

где

w(x, y) является решением краевой задачи

(0,α),

y (0, β), ,

(13)

w = 0,

(14)

w(0, y) = 0, w(α, y) = 0, y (0, β),

182

~		~				(15)
wy (x,0) = g3 (x),		wy (x, β) = g4 (x), x (0,α).
~
и w(x, y) является решением краевой задачи
~		x (0,α),	y (0, β),			(16)
w = 0,
~	~		(y),		y (0, β),	(17)
w(0, y) = g1 (y), w(α, y) = g2
~	~	(x, β) = 0,	x (0,α).			(18)
wy (x,0) = 0,	wy
3. Решение задачи (13)-(15) ищем в виде
~		∞		π
w(x, y) = ∑Bm (y)sin				α	mx.	(19)
		m=1

Эта функция удовлетворяет граничным условиям (14) при любых коэффициентах Bm (y), при которых ряд (19) сходит-

ся. Найдем коэффициенты Bm (y), при которых функция (19)

является решением уравнения (13).

Подставляя функцию (19) в уравнение (13), получаем

∞		π		2		π	mx = 0.
∑	=		α	m	Bm (y)+ Bm′′(y) sin	α	mx = 0.
m=1			α			α

Поэтому
	π	2
Bm′′(y)−	α m	Bm (y) = 0, m =1,2,...

Общее решение этого уравнения имеет вид

Bm (y) = am ch απ my + bm sh απ my.

Следовательно,

~	∞	π	my + bm sh	π		π	mx.	(20)
w(x, y) = ∑ am ch		α		α	my sin	α
	m=1

Эта функция удовлетворяет граничным условиям (14) и является решением уравнения (13) при любых am и bm , при

которых ряд (20) сходится и его можно дважды дифференцировать почленно. Найдем коэффициенты am и bm , при кото-

183

рых функция (20) удовлетворяет граничным условиям (15). Имеем

∞

π mbm sin

π mx = g3 (x),

∑

m=1

∞

mam sh

mβ +

mbm ch

= g4

(x).

∑

mβ sin

m=1

Отсюда в силу формул Эйлера-Фурье следует, что

(x)sin π mxdx,

2πm ∫0

am sh απ mβ + bm ch απ mβ =

g4 (x)sin απ mxdx,

∫0

2πm

Подставляя найденные по этим формулам am и bm в (20), по-

лучаем	~
	w(x, y).
4. Решение задачи (16)-(18) ищем в виде
	~	∞	π	ny.	(21)

	w(x, y) = ∑An (x)cos		β
		n=0
Эта функция удовлетворяет граничным условиям (18) при
любых коэффициентах An (x), при которых ряд (21) сходится

и его можно дифференцировать почленно по у. Найдем коэффициенты An (x), при которых функция (21) является ре-

шением уравнения (16).

Подставляя функцию (21) в уравнение (16), получаем

∞				π			2		π
∞	A′′(x)−					n	A (x) cos ny = 0.
∑	A′′(x)−					n	A (x) cos ny = 0.
∑		n			β		n		β
n=0					β				β

Поэтому
A′′(x)			π		2	A	(x)	= 0,	n = 0,1,2,...
A′′(x)			−	n		A	(x)	= 0,	n = 0,1,2,...
n			β			n

Общее решение этого уравнения имеет вид

184

A0 (x) = a0 + b0 x,

(x) = a

ch π nx + b sh

π nx,

n =1,2,...

Следовательно,

+ b x +

∞

+ b sh

ny.

(22)

w(x, y) = a

nx cos

∑ n

n=1

Эта функция удовлетворяет граничным условиям (18) и

является решением уравнения (16) при любых

и bn ,

при

которых ряд (22) сходится и его можно дважды дифференцировать почленно. Найдем коэффициенты an и bn , при кото-

рых функция (22) удовлетворяет граничным условиям (17). Имеем

∞

π ny = g1(y),

a0 + ∑an cos

n=1

∞

nα + bn sh

ny = g2

(y).

a0 + b0α + ∑ anch

nα cos

n=1

Отсюда в силу формул Эйлера-Фурье следует, что

a0 =

∫g1 (y)dy,

g1 (y)cos

an =

∫0

β nydy,

n =1,2,...,

2β

a0 + b0α =

∫g2 (y)dy,

g2 (y)cos

an ch β nα

+ bn ch β nα =

∫0

β nydy, n =1,2,...

2β

Подставляя найденные по этим формулам an и bn в (22), по-

~( )

лучаем w x, y .

5. Записываем ответ согласно формулам (4) и (12).

185

Замечания.

1.Изложенный план пригоден для решения краевых задач для уравнения Пуассона в разнообразных ограниченных областях плоскости или пространства. Необходимо только, чтобы для этих областей были известны собственные функции оператора Лапласа и решения краевых задач для уравнения Лапласа.

2.Иной план решения задачи (1)-(3) состоит в следую-

щем.

Сначала находим любое решение v уравнения Пуассона

(1). Затем находим решение задачи w = 0,

w(0, y) = g1 (y)−υ(0, y), w(α, y) = g2 (y)−υ(α, y), y (0, β), wy (x,0)= g3 (x)−υy (x,0), wy (x, β)= g4 (x)−υy (x, β), x (0,α).

Решение задачи (1)-(3) определяется формулой (4).

3. Чтобы найти решение v уравнения Пуассона (1), можно перейти в (1) к полярным координатам и применить метод, изложенный в задаче 11.

Пример. Решить краевую задачу для уравнения Пуассона

в прямоугольнике			y (0,2),
u = xy(1 − x), x (0,1),			y (0,2),		(23)
u(0, y) = y2 − y3 / 3	+1,	u(1, y) = 3y2	− y3 + 2,	y (0,2),	(24)
uy (x,0) = x(1	− x),	uy (x,2) = x(1 − x)2 ,		x (0,1).	(25)
План решения. Искомая функция u(x, y) может быть
представлена в виде
	xu(x, y) =υ(x, y)+ w(x, y),				(26)

гдеυ(x, y)— решение краевой задачи для уравнения Пуассо-

на с однородными граничными условиями.
υ = xy(1 − x), x (0,1),	y (0,2),	(27)
υ(0, y) =υ(1, y) = 0,	y (0,2),	(28)
186

υy (x,0) =υy (x,2) = 0,

x (0,1),

(29)

w(x, y) — решение краевой задачи для уравнения Лапласа:


w = 0,	x (0,1),		y (0,2),	(30)
w(0, y) = y2 − y3 / 3 +1,		w(1, y) = 3y2 − y3 + 2, y (0,2),		(31)
wy (x,0) = x(1 − x),		wy (x,2) = x(1 − x)2 , x (0,1).		(32)

1. Решение задачи (27)-(29) ищем в виде ряда по собственным функциям оператора Лапласа с граничными усло-

виями (28)-(29) (задача 10):

∞ ∞	π ny.
υ(x, y) = ∑∑Amn sin πmx cos	π ny.	(33)
m=1 n=0	2

Эта функция удовлетворяет граничным условиям (28)- (29) при любых Amn , при которых ряд (33) сходится и его

можно дифференцировать почленно по у. Найдем коэффициенты Amn , при которых функция (33) является решением

уравнения (27).

Подставляя функцию (33) в уравнение (27), имеем

∞ ∞

πn 2

ny = xy(1

− x).

− ∑∑Amn (πm)

sin πmx cos

m=1 n=0

Отсюда в силу формул Эйлера-Фурье следует, что

= −

1 2

xy(1 − x)sin πmxdydx,

4(πm)2

∫∫0 0

= −

1 2

xy(1 − x)sin πmx cos π nydydx.

8[(πm)2 + (πn / 2)2 ]∫∫0 0

Вычисляя интегралы, получаем

(−1)m −1

[1 − (−1)m ][1 − (−1)n ]

Am0 =

Amn =

π5m3n2 [(πm)2 + (πn / 2)2 ].

(πm)5

Подставляя эти коэффициенты в (33), находим υ(x, y): 187

υ(x, y)

∞

(−1)m −1

= ∑

sin

πmx +

m=1

(πm)

∞ ∞

[1 − (−1)m ][1 − (−1)n ]

+ ∑∑

sin

πmx cos

ny.

(34)

[(

]

m=1 n=1

( n / 2)

2. Решение задачи (30)-(32) ищем в виде

(35)

w(x, y) = w(x, y)+ w(x, y),

где w(x, y) является решением краевой задачи

= 0,

x (0,1),

y (0,2),

(36)

y (0,2),

(37)

w(0, y) = 0,

w(1, y) = 0,

(x,0)

(x,2)

= x(1 − x)

x (0,1).

(38)

= x(1 − x), wy

и w(x, y) является решением краевой задачи

x (0,1),

y (0,2),

(39)

w = 0,

− y

/ 3

+1,

− y

+ 2,

y (0,2),

(40)

w(0, y) = y

w(1, y) = 3y

(0,1).

(41)

wy (x,0)= 0,

wy (x,2)= 0,

3. Решение задачи (36)-(38) ищем в виде

∞

(42)

w(x, y) = ∑Bm (y)sin πmx.

m=1

Эта функция удовлетворяет граничным условиям (37) при любых коэффициентах Bm (y), при которых ряд (42) сходит-

ся. Найдем коэффициенты Bm (y), при которых функция (42)

является решением уравнения (36).

Подставляя функцию (42) в уравнение (36), получаем

∑∞ [− (πm)2 Bm (y)+ Bm′′(y)]sin πmx = 0.

m=1

Поэтому

Bm′′(y)− (πm)2 Bm (y) = 0, m =1,2,...

Общее решение этого уравнения имеет вид

Bm (y) = am chπmy + bm shπmy.

188

Следовательно,

∞
~	(43)
w(x, y)= ∑(amchπmy + bmshπmy)sinπmx .	(43)

m=1

Эта, функция удовлетворяет граничным условиям (37) и является решением уравнения (36) при любых am и bm , при

которых ряд (43) сходится и его можно дважды дифференцировать почленно. Найдем коэффициентыam и bm , при кото-

рых функция (43) удовлетворяет граничным условиям (38). Имеем

∞

∑πmbm sin πmx = x(1 − x),

m=1

∞

(πmam sh2πm +πmbm ch2πm)sin πmx = x(1 − x)2 .

∑

m=1

Отсюда в силу формул Эйлера—Фурье следует, что

x(1 − x)sin πmxdx,

2πm

∫0

sh2πm

+ b ch2πm

x(1 − x)2 sin πmxdx,

2πm ∫0

Вычисляя интегралы, имеем

b =

− (−1)m

, a sh2πm + b ch2πm =

(−1)m

(πm)4

Следовательно,

2 + (−1)m

1 − (−1)m ch2πm

am =

−

(πm)4 sh2πm

(πm)4

sh2πm

Подставляя найденные am и bm в (43), получаем

w(x, y):

∞

2 +

(−

w(x, y) = ∑

chπmy sin

πmx −

(πm)

sh2πm

m=1

189

∞	1 −	(−1)	m	chπm(2 − y)sin πmx.
− ∑							(44)
		4
m=1 (πm)		sh2πm
4. Решение задачи (39)-(41) ищем в виде
~		∞			π
w(x, y) = ∑An (x)cos					2	ny.	(45)
		n=0
Эта функция удовлетворяет граничным условиям (41) при
любых коэффициентах	An (x), при которых ряд (45) сходится

и его можно дифференцировать почленно по у. Найдем коэффициенты An (x), при которых функция (45) является ре-

шением уравнения (39).

Подставляя функцию (45) в уравнение (39), получаем

∞	π		2		π	ny = 0.
∑ An′′(x)−		2	n	An (x) cos	2	ny = 0.
n=0		2			2

Поэтому
	π			2	(x) = 0,	n = 0,1,2,...
A′′(x)−		2	n	A	(x) = 0,	n = 0,1,2,...
n		2		n

Общее решение этого уравнения имеет вид

A0 (x) = a0 + b0 x,

(x) = a

ch π nx + b sh π nx,

n =1,2,...

Следовательно,

∞

nx + bn sh

ny.

(46)

w(x, y) = a0

+ b0 x + ∑ an ch

nx cos

n=1

Эта функция удовлетворяет граничным условиям (41) и является решением уравнения (39) при любых an и bn , при

которых ряд (46) сходится и его можно дважды дифференцировать почленно. Найдем коэффициенты an и bn , при кото-

рых функция (46) удовлетворяет граничным условиям (40). Имеем

190

∞

π ny

+ ∑an

cos

= y2

−

+1,

n=1

a0 + b0

∞

+ bn sh

ny =

− y

+ 2.

+ ∑ an ch

n cos

n=1

Отсюда в силу формул Эйлера-Фурье следует, что

−

∫ y

+1 dy =

1 2 4

[(−1)

−1],

nydy =

−

∫ y

1 cos

πn

a0 + b0

∫2 (3y2 − y3 + 2)dy = 4,

2 4

[(−1)

−1],

anch

n +bn sh

∫(3y

− y

+2)cos

nydy=

πn

Подставляя найденные an и bn

в (46), получаем w(x, y):

w(x, y) =

x +

∞

4 (−1)n

−1

πn

∑

3sh

x + sh

(1 − x) cos

ny.

(47)

2 n=1

πn

sh(πn / 2)

5.Записываем ответ согласно формулам (26), (34), (35),

(44)и (47).

13.Уравнение Пуассона в шаре

Постановка задачи. Решить краевую задачу Дирихле для

уравнения Пуассона в шаре:
u = Axy + Bxz + Cyz,	0 ≤ r < r0 ,	(1)
u \|r =r = a		(2)
0

(r = x2 + y2 + z 2 ).

План решения. Решение краевой задачи (1)-(2) имеет вид

u(x, y, z) = uчн (x, y, z)+υ(x, y, z),

где uчн — какое-нибудь частное решение уравнения (1) и

υ — решение	однородного уравнения	u = 0 ,	удовлетво-
ряющее граничному условию υ \|r=r = a −uчн \|r =r .
	0	0
1.Используя принцип суперпозиции, частное решение
уравнения (1) ищем в виде
где	uчн = u1 + u2 + u3 ,
где	+ y2 + z 2 )— решение уравнения
u1 = Exy(x2	+ y2 + z 2 )— решение уравнения		u = Axy,
u2 = Lxz(x2	+ y2 + z 2 ) — решение уравнения		u = Bxz,
u3 = Myz(x2	+ y2 + z 2 ) — решение уравнения		u = Cyz.

Подставляя u1 в уравнение

u = Axy,

получаем 14Exy = Axy. Следовательно, E = A /14. Аналогич-

но находим L = B /14			и M = C /14. Таким образом,
	2		2				2						A							B						C
uчн = (x		+ y			+ z			)							xy		+					xz +						yz .
uчн = (x		+ y			+ z			)			14				xy		+		14			xz +			14			yz .
2. Функция											14								14						14
2. Функция																		A						B							C
				2				2							2			A						B							C
υ(x, y, z) = u(x, y, z)− (x					+ y					+ z						)				xy +						xz			+			yz (3)
υ(x, y, z) = u(x, y, z)− (x					+ y					+ z						)	14			xy +			14			xz			+	14		yz (3)
																	14						14							14
удовлетворяет уравнению Лапласа
		υ = 0,						0 ≤ r < r0 ,																								(4)
и граничному условию
		2			A								B							C
υ \|r=r = a − r0						xy +										xz +						yz							.			(5)
υ \|r=r = a − r0				14		xy +						14				xz +				14		yz				r=r			.			(5)
0				14								14								14						r=r
0
3. Легко проверить, что функция																												0
																												0

υ(x, y, z) = a − r							2				A			xy +					B		xz +				C		yz

									14									14						14
						0			14									14						14
														192

191

является решением задачи Дирихле (4)-(5). В силу теоремы о единственности решения задачи Дирихле для уравнения Лапласа в шаре других решении нет.

4. Подставляя v(x,y,z) в равенство (3), получаем

u(x, y, z) = (x

+ y

+ z

− r0

)

xy +

xz +

+ a.

Замечание. В п. 1 при отыскании частных решений u1 ,u2 и u3 использовано следующее свойство уравнения Пуассона.

Если P(x, y, z) — однородный многочлен степени n , то уравнение u = P(x, y, z) имеет решение u = Q(x, y, z), где Q

— однородный многочлен степени n + 2 .

Например, уравнение u = x2 y2 имеет решение
u =	x2 y2	−		x6	.
u =	12	−	180		.
	12		180
Пример. Решить краевую задачу Дирихле для уравнения
Пуассона в шаре
u =14xy,		0 ≤ r < 2 ,				(6)
u \|r =2 =14.						(7)
Решение.
1. Частное решение уравнения (6) ищем в виде
uчн = E(x2 + y2 + z 2 )xy.
Подставляя его в уравнение (6), получаем
6Exy + 6Exy + 2Exy =14xy.
Следовательно, E =1 и
uчн = (x2 + y2 + z 2 )xy.
2. Функция
υ(x, y, z) = u(x, y, z)− (x2 + y2 + z 2 )xy						(8)
удовлетворяет уравнению Лапласа
u = 0,				0 ≤ r < 2,		(9)
и граничному условию
υ \|r =2 =14 − 4xy \|r=2 .						(10)

3.Легко проверить, что функция w(x, y, z) =14 − 4xy яв-

ляется решением задачи Дирихле (9)-(10). В силу теоремы о единственности решения задачи Дирихле для уравнения Лапласа в шаре других решений нет.

4. Подставляя υ(x, y, z) в равенство (8), получаем u(x, y, z) =14 − 4xy + (x2 + y2 z 2 )xy.

Ответ. u(x, y, z) =14 − 4xy + (x2 + y2 z 2 )xy.

14. Однородное волновое уравнение на отрезке

Постановка задачи. Решить первую смешанную задачу

для однородного волнового уравнения на отрезке
utt − a2uxx = 0,	x (0,l), t (0, ∞),		(1)
u(x,0) = f (x),	ut (x,0) = g(x),	x (0,l),	(2)
u(0,t) = u(l,t) = 0,		t (0, ∞).	(3)

План решения.

1.Находим вспомогательные решения υ(x,t) уравнения

(1)в виде

υ(x, t)= X (x)T (t),

причем υ(0,t) =υ(l,t) = 0, т.е. X (0) = X (l) = 0. Для этого подставляем υ(x,t) = X (x)T (t) в уравнение (1) и разделяем пере-

менные. Получаем

XX′′ = aT2T′′ = λ = const.

Поэтому функции X (x)и T (t) являются решениями свя-

занных задач:

а) X ′′(x)− λX (x) = 0, X (0) = X (l) = 0;

б) T ′′− λa2T = 0. 3. Решаем задачу (а).

Уравнение X ′′ − λX = 0 имеет общее решение

194

193

X (x) = Ce λx + De− λx .

Из граничных условий X (0) = X (l) = 0 следует, что

πn 2

X n

= Cn sin

πn

n =1,2,...

λn = −

Решаем задачу (б). При λ = λn

= −(πn / l)2

имеем

T ′′+

πn

T = 0.

Общее решение этого уравнения есть

πn

Tn (t) =

πn

at.

An cos

at + Bn sin

Итак, вспомогательные решения уравнения (1) имеют

вид

πn

(x,t) = C

cos

at + B

sin

x =

at sin

n n

cos

πn

at + B

sin

πn

at sin

— постоянные, которые предсто-

где An = Cn An ,

= Cn Bn

ит найти.

5. Решение задачи (1)-(3) ищем в виде

πn

∞

πn

at +

Bn sin

x. (4)

u(x,t) = ∑υn (x,t) = ∑ An cos

at sin

n=1

Эта функция является решением уравнения (1) и удовлетворяет граничным условиям (3) при любых An и Bn , при кото-

рых ряд (4) сходится и его можно дважды дифференцировать почленно.

7. Находим коэффициенты An и Bn , при которых u(x,t)

удовлетворяет начальным условиям (2). Полагая в (4) t = 0 , получаем

195

u(0,t)

∞

sin πn x = f (x).

= ∑An

Отсюда

n=1

2 l

f (x)sin

πn

∫0

l xdx.

Дифференцируя равенство (4), имеем

πna

πn

∂u

∞

πna

An sin

πna

t +

πna

Bn cos

∂t

= ∑ −

t sin

n=1

Полагая здесь t = 0

и используя начальное условие (2),

получаем

∞

Bn sin πn x = g(x).

∑πna

Отсюда

n=1

2 l

πn

Bn =

∫0

g(x)sin l

xdx.

πna

Подставляя эти коэффициенты в формулу (4), получаем искомое решение и записываем ответ.

Замечание. При каждом фиксированном t ряд (4) является разложением u(x,t)по системе собственных функций

оператора Лапласа на отрезке (0,l):

υxx = λυ, x (0,l),

υ(0) =υ(l) = 0.

Задача (а) состоит в отыскании этих собственных функций и соответствующих им собственных значений λ . Коэффициенты при t в (4) являются квадратными корнями из собственных значений λ.

Пример. Решить первую смешанную задачу для однородного волнового уравнения на отрезке

196

utt − 4uxx = 0,	x (0,1), t (0, ∞),	(5)
u(x,0) = 0,	ut (x,0) = x(1 − x),	(6)
u(0,t) = u(1,t) = 0.		(7)

Решение.

1. Находим вспомогательные решения υ(x,t) уравнения

(5) в виде

υ(x,t) = X (x)T (t),

причем υ(0,t) =υ(1,t) = 0, т.е. X (0) = X (1) = 0. Для этого под-

ставляем функцию v(x,t) = X(x)T(t) в уравнение (5) и разделяем переменные. Получаем

	X ′′	=	T ′′	= λ.

	X		4T
Поэтому функции X (x) и T (t) являются решениями связан-
ных задач:	X (0) = X (1) = 0;
′′
а) X (x)− λX (x) = 0,

б) T ′′− 4λT = 0.

3. Решаем задачу (а). Уравнение X ′′− λX = 0 имеет общее решение

X (x) = Ce λx + De− λx .

Из гранитных условий X (0) = X (1) = 0 следует, что

λn = −(πn)2 ,	X n = Cn sin πnx,	n =1,2,...
4. Решаем задачу (б). При λ = λn = −(πn)2			имеем
	Tn′′+ 4(πn)2 Tn = 0.
Общее решение этого уравнения есть
~	~
Tn = An cos 2πnt + Bn sin 2πnt.
5. Итак, вспомогательные решения уравнения (5) имеют
вид	~
~		πnx	=
υn (x, t)= Cn (An cos 2πnt + Bn sin 2πnt)sin
	= (An cos 2πnt + Bn sin 2πnt)sin πnx,
	197

где	~	~
где	An = Cn An ,	Bn = Cn Bn — постоянные, которые предстоит
найти.
	6. Решение задачи (5)-(7) ищем в виде
	∞	∞	(An cos 2πnt + Bn sin 2πnt)sin πnx. (8)
	u(x,t) = ∑υn (x,t) = ∑		(An cos 2πnt + Bn sin 2πnt)sin πnx. (8)
	n=1	n=1

Эта функция является решением уравнения (5) и удовлетворяет граничным условиям (7) при любых An и Bn , при ко-

торых ряд (8) сходится и его можно дважды дифференцировать почленно.

7.Находим коэффициенты An и Bn , при которых u(x,t)

удовлетворяет начальным условиям (6). Полагая в (8) t = 0 получаем

Общее решение этого уравнения есть

∞

∑An sin πnx = 0.

n=1

Отсюда An = 0.

Дифференцируя равенство (8), имеем

∂∂u = ∑∞ (− 2πnAn sin 2πnt + 2πnBn cos 2πnt)sin πnx. t n=1

Полагая здесь t = 0 и используя начальное условие (6), получаем

∞

∑2πnBn sin πnx = x(1 − x).

n=1

Отсюда в силу формул Эйлера-Фурье следует, что

B2k +1 =	4	, B2k	= 0.
	π 4 (2k +1)4

Подставляя найденные коэффициенты в формулу (8), получаем

∞			4
u(x,t) = ∑			4		sin 2π(2k +1)t sin(2k +1)πx.
u(x,t) = ∑	π	4	(2k +1)	4	sin 2π(2k +1)t sin(2k +1)πx.
k =0	π		(2k +1)	198
				198

∞			4
Ответ. u(x,t) = ∑			4		sin 2π(2k +1)t sin(2k +1)πx.
Ответ. u(x,t) = ∑	π	4	(2k +1)	4	sin 2π(2k +1)t sin(2k +1)πx.
k =0	π		(2k +1)

15. Неоднородное волновое уравнение на отрезке

Постановка задачи. Решить первую смешанную задачу

для неоднородного волнового уравнения на отрезке:
utt − a2uxx	= α sin	π x + 4β sin3 π x +16γ sin5 π x,			(1)
		l	l	l
x (0,l), t (0, ∞),
u(x,0) = 0,	ut (x,0) = 0,		x (0,l),		(2)
u(0,t) = u(l,t) = 0,		t (0, ∞).			(3)

План решения.

1. Разлагаем правую часть уравнения (1) в ряд Фурье по системе собственных функций оператора Лапласа на отрезке

(0,l):

υxx

= λυ,

x (0,l),

υ(0) =υ(l) = 0,

т.е. по системе функций sin(πx / l),

sin(2πx / l), sin(3πx / l),...

Имеем

α sin

π x + β sin3 π x +γ sin5 π x =

= (α + 3β +10γ )sin π x −

(β + 5γ )sin

3π

x +γ sin

5π

Решение задачи (1)-(3) ищем в виде

u(x,t) = u

(t)sin π x + u

(t)sin

3π

x + u

(t)sin

5π

(4)

3. Подставляя выражение (4) в уравнение (1), получаем систему дифференциальных уравнений:

199

′′

π 2

α + 3β +10γ,

u1(t)+ l2 a u1(t)=

9π 2

(t)

= −(β + 5γ ),

(5)

u′′(t)

25π

(t)= γ.

u5′′(t)

a2u5

4. Начальные условия (2) эквивалентны следующим на-

чальным условиям для системы (4):

u1 (0) = u1′(0)

= 0, u3 (0)

= u3′(0), u5 (0) = u5′(0) = 0.

5. Решая последовательно задачу Коши для каждого

уравнения системы (4), получаем

u1 (t) =

(α

+ 3β +

10γ )l 2

− cos

πα

(6)

π 2 a

t ,

u3 (t)

− (β + 5γ )l 2

3πa

9π 2 a2

1 − cos

(7)

(t) =

γl 2

5πa

− cos

t .

(8)

25π 2 a2

6. Подставляя (6)-(8) а формулу (4), получим искомое

решение задачи (1)-(3):

u(x,t) =

(α + 3β +10γ )l

πa

− cos

t sin

x −

π 2 a2

(β + 5γ )l 2

3πa

3π

γl 2

5πa

5π

−

1 − cos

t sin

x +

− cos

t sin

9π 2 a2

25π 2 a2

Замечание. Аналогично решается задача

utt − a2uxx = f (x), x (0,l), t (0, ∞),

u(x,0) = 0, ut (x,0) = 0, x (0,l),

u(0,t) = u(l,t) = 0, t (0, ∞).

f (x).

при произвольной непрерывной функции

200

Пример. Решить первую смешанную задачу для неодно-

родного волнового уравнения на отрезке
utt −uxx = 4sin3 x,	x (0,π ), t (0, ∞),	(9)
u(x,0) = 0, ut (x,0) = 0, x (0,π ),		(10)
u(0,t) = u(π,t) = 0,	t (0, ∞).	(11)
Решение.
1. Разлагаем правую часть уравнения (1) в ряд Фурье по

системе собственных функций оператора Лапласа на отрезке

(0,π ):

υxx	= λυ, x (0,π ),
υ(0) =υ(π ) = 0,

т.е. по системе функций sin x, sin 2x, sin 3x,... Имеем

4sin3 x = 3sin x −sin 3x.

2. Решение задачи (9)-(11) ищем в виде
u(x,t)= u1(t)sin x + u3 (t)sin 3x.	(12)

3. Подставляя выражение (12) в уравнение (9), получаем систему дифференциальных уравнений:

u1′′(t)+ u1(t)= 3, (13)

u3′′(t)+ 9u3 (t)= −1.

4.	Начальные условия (10) эквивалентны следующим ус-
ловиям для системы (13):
	u1 (0) = u1′(0) = 0, u3 (0) = u3′(0) = 0. .
5.	Решая последовательно задачу Коши для каждого у
системы (13), получаем
	u1 (t) = 3(1 − cos t),			(14)
	u3 (t) = −	1	(1 − cos3t).	(15)

	9
6.	Подставляя (14) и (15) в формулу (12), получаем иско-
мое решение задачи (9)-(11):
	201

u(x,t) = 3(1 − cos t)sin x − 19 (1 − cos3t)sin 3x. Ответ. u(x,t) = 3(1 − cos t)sin x − 19 (1 − cos3t)sin 3x.

16. Однородное волновое уравнение в прямоугольнике

Постановка задачи. Решить первую смешанную задачу

для однородного волнового уравнения в прямоугольнике:
utt = a2 u,	x (0,α), y (0, β), t (0, ∞),	(1)
u(x, y,0) = 0,	ut (x, y,0) = Axy(α − x)(β − y),	(2)
u(0, y,t) = u(x,0,t) = u(α, y,t) = u(x, β,t) = 0.		(3)

План решения.

1. Находим вспомогательные решения уравнения (1) в виде

υ(x, y,t) = X (x)Y (y)T (t),

причем v(0, y,t)= v(x,0,t)= v(α, y,t)= v(x, β,t)= 0, т.е. X (0) =

=X (α) = 0, Y (0) = Y (β) = 0.Для этого подставляем функцию

υ(x, y,t)в уравнение (1) и разделяем переменные. Получаем

X ′′

Y ′′

T ′′

Поэтому функции X (x), Y (y) и T (t) являются решениями

связанных задач:

X (0) = X (α) = 0;

а) X ′′− λX = 0,

б) Y ′′− μY = 0, Y (0) = Y (β) = 0;

в) T′′− a2 (λ + μ)T = 0.

2. Решаем задачи (а) и (б). Получаем

= −π

= A sin

πn

n =1,2,...,

α 2

= −π

2 m2

= B

sin

πm

m =1,2,...

β 2

202

n=1 m=1

3. Решаем задачу (в). При λ + μ = λn + μm = −π

2 +

имеем

′′

+π

= 0.

Общее решение этого уравнения есть

= A

cosπa

t + B

sinπa

α2

β2

α2

4. Итак, вспомогательные решения уравнения (1) имеют

вид

(x, y,t) = C

cosπa

t +

α 2

sinπa

πn

xsin

πm

+ B

sin

A cosπa

+ m

t + B

sin πa

+ m

πn x sin

πm y,

sin

α 2

где

Anm

Bnm

постоянные,

которые

= Cnm Anm ,

= Cnm Bnm —

предстоит найти.

5. Решение задачи (1)-(3) ищем в виде

∞ ∞

∞

(Anm cosπa

u(x, y,t) = ∑∑υnm =

∑∑

2 + m

2 t +

n=1 m=1

α β

+ Bnm sin πa

πn

x sin

πm

(5)

α 2

β 2

sin

Эта функция является решением уравнения (1) и удовлетворяет граничным условиям (3) при любых Anm и Bnm , при ко-

203

торых ряд (5) сходится и его можно дважды дифференцировать почленно.

6. Находим коэффициенты Anm и Bnm , при которых u(x,t)

удовлетворяет начальным условиям (2). Полагал в (5) t = 0, получаем

u(x, y,0) = ∑∑∞ ∞ Anm sin παn x sin πβm y = 0.

Отсюда Anm = 0 (n =1,2,..., m =1,2,...).

Дифференцируя равенство (5), полагая t = 0 и используя начальное условие (2), получаем

∞

sin πn x sin πm y = Axy(α − x)(β − y).

∑∑Bnmπa

+ m2

n=1 m=1

Отсюда в силу формул Эйлера-Фурье следует, что

− y)sin

πn

πm

Bnmπa

α2

+ β2

= α

∫

∫Axy(α − x)(β

xsin β ydydx.

Следовательно,

(1 − (−1)n )

(1 − (−1)m )=

Bnm =

4Aα 2

4β 2

π 4 n3 a

π 3 m3

α 2

β 2

n = 2k

или m = 2l,

64α 2 β 2 A

n = 2k +1 и

(2k +

1)2

(2l +1)2

7 a

(2k +1)3

(2l +1)3

m = 2l +1.

Подставляя найденные Anm и Bnm

значения

в (5), получа-

ем искомое решение и записываем ответ.

Замечания.

1. Аналогично решается задача

utt = a2 u,

x (0,α), y (0, β), t (0, ∞),

204

u(x, y,0) = f (x, y), ut (x, y,0) = g(x, y), u(0, y,t) = u(x,0,t) = u(α, y,t) = u(x, β,t) = 0

при произвольных достаточно гладких функциях f (x, y) и g(x, y), для которых получающиеся в ответе ряды можно

дважды дифференцировать почленно.

2. При каждом фиксированном t ряд (5) является разложением u(x, y,t)по системе собственных функций оператора

Лапласа в прямоугольнике:
υ = λυ, x (0,α), y (0, β),
υ(0, y) =υ(α, y) =	υ(x,0) =υ(x, β) = 0.

Отыскание этих собственных функций и соответствующих им собственных значений λ сводится к решению задач (а) и (б). Коэффициенты при t в (5) являются квадратными корнями из собственных значений λ .

Пример. Решить первую смешанную задачу для

однородного волнового уравнения в прямоугольнике
utt = 4 u,	x (0,2), y (0,1), t (0, ∞),	(6)
u(x, y,0),	ut (x, y,0) = (2 − x)(1 − y)xy,	(7)
u(0, y,t) = u(x,0,t) = u(2, y,t) = u(x,1,t) = 0.		(8)

Решение.

1. Находим вспомогательные решения уравнения (6) в

виде
υ(x, y,t) = X (x)Y (y)T (t),
причем υ(0, y,t)=υ(x,0,t)=υ(2, y,t)=υ(x,1,t)= 0, т.е.	X (0) =
= X (2) = 0, Y (0) = Y (1) = 0. Для этого подставляем	функ-

циюυ(x, y,t) в уравнение (6) и разделяем переменные. Полу-

чаем

XX′′ + YY′′ = aT2T′′ .

Поэтому функции X (x),Y (y)и T (t) являются решениями свя-

занных задач:

205

а)	X ′′− λX = 0, X (0) = X (2) = 0;
б) Y ′′− μY = 0, Y (0) = Y (1) = 0;
в)	T′′− 4(λ + μ)T = 0.

2. Решаем задачи (а) и (б). Получаем

= −π

A sin

πn

n =1,2,...,

= −π 2 m2 ,

= A sin πmy,

m =1,2,...

3. Решаем задачу (в). При λ + μ = λn + μm

= −π

+ m

имеем T′′+π 2 (n2 + 4m2 )T = 0 .

Общее решение этого уравнения есть

= A

cosπ

+ 4m2 t + B

sinπ

n2 + 4m2

t .

n m

Итак, вспомогательные решения уравнения (1)

имеют

вид

υnm (x, y,t) = Cnm (Anm cosπ

+ 4m

t) sin

πn

x sin πmy =

+ Bnm sin π

= (Anm cosπ n2

+ 4m2 t)sin

πn x sin πmy,

+ 4m2 t + Bnm sin π

Bnm

— постоянные, которые пред-

где Anm = Cnm Anm ,

= Cnm Bnm

стоит найти.

Решение задачи (6)-(8) ищем в виде

∞

(Anm cosπ

u(x, y,t) = ∑∑υnm (x, y,t) = ∑∑

n2 + 4m2 t +

n=1 m=1

+ Bnm sin π

+ 4m2 t) sin πn x sin πmy.

(9)

Эта функция является решением уравнения (6) и удовлетворяет граничным условиям (8) при любых An и Bn , при кото-

206

рых ряд (9) сходится и его можно дважды дифференцировать почленно.

6. Находим коэффициенты An			и Bn , при которых u(x,t)
удовлетворяет начальным условиям (7).
Полагая в (9) t	= 0, получаем
∞	∞
∑∑Anm sin πn x sin πmy = 0.
n=1 m=1		2
Следовательно, Anm = 0,		n =1,2,...,	m =1,2,...

Дифференцируя равенство (9), полагая t = 0 и используя начальное условие (7), получаем

∞	∞		2 + 4m2 sin πn x sin πy = xy(2 − x)(1 − y).
∑∑Bnmπ		n
n=1 m=1				2
Отсюда в силу формул Эйлера-Фурье следует, что
			2 1		πn x sin πmydydx.
Bnmπ	n2 + 4m2		= 2∫∫xy(2 − x)(1 − y)sin
Следовательно,			0	0	2
				256
B2k +1,2l +1 =						,
		π 2 (2k +1)2 + 4(2l +1)2 (2k +1)3 (2l +1)3

B2k ,m = 0, n =1,2,..., k =1,2,..., Bn,2l = 0, m =1,2,..., l =1,2,...

Подставляя найденные значения Anm и Bnm в (9), получа-

ем

Ответ.

∞ ∞			256
u(x, y,t) = ∑∑			256		×
u(x, y,t) = ∑∑		π 7			×
k =1 l=1		π 7	(2k +1)2 + 4(2l +1)2 (2l +1)3 (2l +1)3
×sin π	(2k +1)2 + 4(2l +1)2 t sin			π(2k +1) x sin π(2l +1)y.
				2
			207

17. Задача Коши для волнового уравнения на прямой

Постановка задачи. Решить задачу Коши для волнового

уравнения на прямой:
utt = a2uxx , t (0, ∞), x (− ∞, ∞),		(1)
u(x,0) = u0 (x),	x (− ∞, ∞),	(2)
ut (x,0) = u1 (x),	x (− ∞, ∞).	(3)
План решения. Общее решение уравнения (1) имеет вид
u(x,t) = f (x + at)+ g(x − at),		(4)

где f и g — произвольные дважды дифференцируемые функции (задача 2). Требуется найти конкретные функции f и g такие, что выполняются начальные условия (2) и (3).

1. Из (2) и (3) получаем

f (x)

+ g(x) = u0 (x),

(5)

f ′(x)− g′(x) =

u1 (x).

f (x) и g(x). Для

2. Решаем систему (5) относительно

этого дифференцируем первое уравнение. Получаем

f ′(x)

+ g′(x) = u′

(x),

u1 (x).

f ′(x)

− g′(x) =

Отсюда

f ′(x) =

u0′

(x)+

(x),

g′(x) =

u0′

(x)−

(x).

Интегрируя эти равенства, получаем

208

f (x) =

(x)+

x u (y)dy

+ C

2a ∫0

g(x) =

(x)−

∫u1 (y)dy + C2 ,

где C1

C2 — произвольные постоянные.

Используя (4), получаем

u(x,t)

u0 (x + at)+

x+at

(y)dy + C1 +

∫0 u1

x−at

u0 (x − at)−

∫0 u1 (y)dy + C2 =

(x + at)+

(x − at)+

x+at

(y)dy + C + C

2a x−∫at 1

4. Из условия (2) следует, что

u0 (x)+ C1 + C2 = u0 (x).

Поэтому C1 + C2 = 0. Записываем ответ

u(x,t) = 12 u0 (x + at)+ 12 u0 (x − at)+ 21a

x+at	(y)dy.
∫u1	(y)dy.	(6)

x−at

Замечание. Равенство (6) называется формулой Даламбе-

ра.

Пример. Решить задачу Коши для волнового уравнения

на прямой:		t (0, ∞), x (− ∞, ∞),
utt = 4uxx ,		t (0, ∞), x (− ∞, ∞),			(7)
u(x,0) = e−x2 ,			x (− ∞, ∞),		(8)
ut (x,0) =		1		, x (− ∞, ∞).	(9)
ut (x,0) =	1	+ x2		, x (− ∞, ∞).	(9)
	1	+ x2
План решения. Общее решение уравнения (7) имеет вид
u(x,t) = f (x + 2t)+ g(x − 2t),					(10)
		209

где	f и		g — произвольные										дважды дифференцируемые
функции. Требуется найти конкретные функции																							f и g такие,
что выполняются начальные условия (8) и (9).
1.	Из (8) и (9) получаем
			f (x)+ g(x) = e−x2 ,
																							(11)
															1 1								(11)
			f ′(x) = g′(x)									=			1 1				.

															2 1 + x2
															2 1 + x2								и g(x). Для
2.	Решаем систему (11) относительно f (x)																						и g(x). Для
этого дифференцируем первое уравнение. Получаем
						′(x)+ g′(x)							= −2xe				−x2		,
				f		′(x)+ g′(x)							= −2xe						,
						′(x)− g′(x)									1 1
				f									=		1 1					.

															2 1 + x2
Отсюда															2 1 + x2
Отсюда															1		1
											−x2				1		1
			f ′(x) = −xe										+									,
			f ′(x) = −xe										+		4	1 + x			2			,
															4	1 + x
															1	1
											−x2				1	1
			g′(x) = −xe										−								..
			g′(x) = −xe										−		4	1 + x		2			..
															4	1 + x
Интегрируя эти равенства, получаем
			f (x) =					1	e−x2		+		1	arctgx + C ,
			f (x) =						e−x2		+			arctgx + C ,
							2						4						1
							2						4
							1					1
							1			−x2		1
			g(x)			=			e		−			arctgx + C2 ,
			g(x)			=	2		e		−	4		arctgx + C2 ,
							2					4
гдеC1	и C2 — произвольные постоянные.
3.	Используя (10), получаем
u(x,t) =		1	e−(x+2t )2 +	1	arctg(x + 2t)+ C											+
u(x,t) =			e−(x+2t )2 +		arctg(x + 2t)+ C											+
	2		4												1
	2		4

+12 e−(x−2t )2 − 14 arctg(x − 2t)+ C2 .

5.Из условия (8) следует, что

e−x2 + C1 + C2 = e−x 2 . 210

Поэтому C1 + C2 = 0.

Ответ.

u(x,t) = 12 e−(x+2t )2 + 12 e−(x−2t )2 + 14 arctg(x + 2t)− 14 arctg(x − 2t).

18. Уравнение теплопроводности на отрезке

Постановка задачи. Решить первую смешанную задачу

для уравнения теплопроводности на отрезке:
ut = a2uxx , x (0,l), t (0, ∞),		(1)
u(x,0) = f (x),	x (0,l),	(2)
u(0,t) = u(l,t)	= 0, t (0, ∞).	(3)

План решения.

1. Находим вспомогательные решения уравнения (1) в ви-

де

υ(x,t) = X (x)T (t),

причем υ(0,t)=υ(l,t)= 0, т.е. X (0) = X (l) = 0. Для этого подставляем функцию υ(x,t) = X (x)T (t) в уравнение (1) и разделяем переменные. Получаем

		X ′′	=		T ′	= λ = const.
		X
					a2T
Поэтому функции X (x)				и T (t) являются решениями связан-
ных задач:
а)	′′
	X (x)− λX (x) = 0, X (0) = X (l) = 0;

6) T ′− a2 λT = 0.

3. Решаем задачу (а).

Уравнение X ′′− λX = 0 имеет общее решение

X (x)= Ce λ x + De− λ x .

Из граничных условий X (0) = X (l) = 0 следует, что

	πn		2	X n = Cn sin	πn	x,	n =1,2,...
λn = −	l	,			l
				211

4. Решаем задачу (б). При λ =

λn

πn

= −

имеем

πn

T = 0.

T ′+

Общее решение этого уравнения есть

π n

−

n =1,2,...

= A e

5. Итак, вспомогательные решения уравнения (5) имеют вид

π n 2

πn

π n 2

πn

a t

υn (x,t)= Cn An e

−

x = An e

−

sin

где An = Cn An — постоянные, которые предстоит найти.

6. Решение задачи (1)-(3) ищем в виде

u(x,t)= ∑υn (x,t)

π n 2

sin πn x.

(4)

= ∑An e

a t

∞

−

n=1

Эта функция является решением уравнения (1) и удовлетворяет граничным условиям (3) при любых An , при которых

ряд (4) сходится. Его можно дважды дифференцировать почленно.

7.Находим коэффициенты An такие, что u(x,t)

удовлетворяет начальному условию (2). Полагая в (4) t = 0, получаем

		∞			πn x = f (x).
u(x,0) = ∑An sin
Следовательно,		n=1			l

A	=	2	1	f (x)sin πn xdx.

n		l ∫0			l

Подставляя эти коэффициенты в формулу (4), получаем искомое решение u(x,t) и записываем ответ.

212

Замечание. При каждом фиксированном t ряд (4) является разложением u(x,t) по системе собственных функций оператора Лапласа на отрезке (0,l):

υxx = λυ, x (0,l),

υ(0) =υ(l) = 0.

Задача (а) состоит в отыскании этих собственных функций и соответствующих им собственных значений λ . Коэффициенты при t в (4) являются собственными значениями λ .

Пример. Решить первую смешанную задачу для уравне-

ния теплопроводности на отрезке:
ut = uxx , x (0,1),	t (0, ∞),	(5)
u(x,0) = sin3 2πx,	x (0,1),	(6)
u(0,t) = u(1,t) = 0,	t (0, ∞).	(7)

Решение.

1. Находим вспомогательные решения уравнения (5) в ви-

де

υ(x,t) = X (x)T (t),

причем υ(0,t) =υ(1,t) = 0, т.е. X (0) = X (1) = 0. Для этого подставляем функцию υ(x,t) = X (x)T (t) в уравнение (5) и разделяем переменные:

		X ′′	=	T ′		= λ.
		X	=			= λ.
Поэтому функции X (x)		X		T
Поэтому функции X (x)		и T (t)			являются решениями связан-
ных задач:					(l) = 0;
а)	′′
а)	X (x)− λX (x) = 0, X (0) = X
б)	T ′ − λT = 0.
	3. Решаем задачу (а).

Уравнение X ′′− λX = 0 имеет общее решение.

X (x) = Ce λx + De− λx .

Из граничных условий X (0) = X (l) = 0 следует, что

213

λn = −π 2 n2 ,

X n = Cn sin πnx,

n =1,2,...

Решаем задачу (б). При λ = λn

= −π 2 n2 имеем

T ′+π 2 n2T = 0.

Общее решение этого уравнения есть

= A e−π 2n2t ,

n =1,2,...

Итак, вспомогательные решения уравнения (5) имеют

вид

π n 2

π n

π n 2

πn

(x,t)= C

−

sin

x =

−

A e

sin

n n

где An

= Cn An − постоянные, которые предстоит найти.

Решение задачи (5)-(7) ищем в виде

π n 2

sin πn x.

(8)

u(x, t)= ∑υ(x,t)= ∑Ane

∞

−

n=1

Эта функция является решением уравнения (5) и удовлетворяет граничным условиям (7) при любых An , при которых

ряд (8) сходится. Его можно дважды дифференцировать почленно.

7.Находим коэффициенты An такие, что u(x,t)

удовлетворяет начальному условию (6), которое запишем в виде u(x,0) = sin3 2πx = 34 sin 2πx − 14 sin 6πx .

Полагая в (8) t = 0, получаем

				∞			πn x =	3 sin 2πx −		1 sin 6πx.
		u(x,0)= ∑An sin					πn x =	3 sin 2πx −		1 sin 6πx.
Отсюда			n=1				l	4		4
Отсюда	3			1
A =	3	,	A = −	1	, A = A = A = A = 0, A = 0, n ≥ 7.
A =		,	A = −		, A = A = A = A = 0, A = 0, n ≥ 7.
2	4		6	4		1	3	4	5	n
	4			4

Подставляя эти коэффициенты в формулу (8), получаем

214

u(x,t) = 34 e−4π 2t sin 2πx − 14 e−36π 2t sin 6πx.

Ответ. u(x,t) = 34 e−4π 2t sin 2πx − 14 e−36π 2t sin 6πx.

19. Уравнение теплопроводности в круге

Постановка задачи. Решить первую смешанную задачу для уравнения теплопроводности в круге:

= a2

0 ≤ r < r ,

t > 0,

(1)

u(r,0) = r

− r 2 ,

0 ≤ r < r ,

(2)

u(r0 ,t)

= 0,

t > 0.

(3)

План решения.

1. Записывая, оператор Лапласа

в полярных координа-

тах, получаем уравнение

∂u

∂

1 ∂u

1 ∂

= a

(4)

2 +

∂t

∂r

r ∂r

∂ϕ

Так как граничное и начальное условия не зависят от ϕ и коэффициенты уравнения также не зависят от ϕ , решение первой смешанной задача (1)-(3) тоже не зависит от ϕ , т.е. u(r,ϕ,t) = u(r,t),

где функция u(r,t) удовлетворяет уравнению (4) с

∂2u / ∂ϕ2 ≡ 0 :

∂u				∂	2	u		1	∂u
		= a	2				+
						2
∂t				∂r				r	∂r	.

2. Находим вспомогательные решения уравнения (5) в
виде	υ(r,t) = R(r)T (t),

причем \| R(0)\|< ∞ и R(r0 ) = 0.						Для этого подставляем функ-

цию υ(r, z) = R(r)T (t) в уравнение (5) и разделяем переменные. Получаем

= −λ = const.

Поэтому функции R(r) и T (t)

являются решениями связан-

ных задач:

а) R′′+

R′+ λa2 R = 0, 0 ≤ r < r0 , | R(0)|< ∞, R(r0 ) = 0.

б) T ′+ λa2T = 0.

4. Решаем задачу (а).

Общее решение уравнения R′′+

R′+ λR = 0 имеет вид

R(r) =

( λr),

AJ0 ( λr)+ BY0

где J0 и Y0 — функции

Бесселя

Неймана. Поскольку

| R(0)|< ∞, а Y0 (r)→ ∞ при r → 0,

полагаем

B = 0..

Используя граничное условие R(r0 ) = 0,

получаем

Rn =

n =1,2,...,

λn =

An J0

r ,

гдеμn —нули функции Бесселя J0 (x), т.е. J0 (μn ) = 0,

n =1,2,...

= (μ

/ r )2 имеем

5. Решаем задачу (б). При λ = λ

′

= 0.

Общее решение этого уравнения есть

T (t)

= B

−

r0 .

6. Итак, вспомогательные решения уравнения (5) имеют вид

216

215

−

= A0 J

υn (r, z) = An Bn J0

r e

где An = An Bn — постоянные, которые предстоит найти.

7. Решение u(r,t) ищем в виде

−

∞

u(r,t) = ∑υn (r,t) = ∑An J

(6)

r e

n=1

Эта функция является решением уравнения (1) и удовлетворяет граничному условию (3) при любых An , при которых

ряд (6) сходится и его можно дважды дифференцировать почленно.

8. Находим, An , при которых u(r,t) удовлетворяет на-

чальному условию (2).

Полагая в (6) t

= 0,

получаем

∞

− r

u(r,0) = ∑An J0

r = r0

n=1

Отсюда в силу формул Эйлера—Фурье следует, что

2∫(r0 − r

)J0

4r 2 J

(μ

)

r rdr

A =

n =1,2,...

r 2 J 2

(μ

)

μ2 J

(μ

)

Подставляя эти коэффициенты в формулу (6), получаем

(μn )

μna

∞

4r0 J 2

−

μn

u(r,t) = ∑

(μ

)

r .

n=1

Замечание. Аналогично решается задача

= a2

0 ≤ r < r , t < 0,

u(r,0) = f

(r), 0 ≤ r < r0 ,

u(r0 ,t) = 0,

t > 0,

217

при произвольной непрерывной функции f (r)такой, что

f (r0 ) = 0.

Пример. Решить первую смешанную задачу для уравне-

ния теплопроводности в круге:

ut =

0 ≤ r <1,

t > 0,

(7)

u(r,0) =1 − r 2 ,

0 ≤ r <1,

(8)

u(1,t) = 0,

t > 0.

(9)

Решение.

1. Записывая оператор Лапласа

в полярных координа-

тах, получаем уравнение

∂u

∂2u

∂u

∂2u

(10)

∂t

∂r 2

∂r

r 2

∂ϕ2

Так как граничное и начальное условия не зависят от ϕ и коэффициенты уравнения также не зависят от ϕ, решение первой смешанной задачи (7)-(9) тоже не зависит отϕ, т.е.

u(r,ϕ,t) = u(r,t),

где функция u(r,t) удовлетворяет уравнению (10) с

∂2u / ∂ϕ2 ≡ 0 :

2.находим вспомогательные решения уравнения (11) в

виде

υ(r,t) = R(r)T (t),

причем | R(0)|< ∞ и R(1) = 0. Для этого подставляем функцию υ(r, z) = R(r)T (t) в уравнение (11) и разделяем переменные. Получаем

d		dR		dT
	r
	r
dr		dr	=	dt	= −λ = const.
			=	T	= −λ = const.
	R			T

Поэтому функции R(r) и T (t) являются решениями связанных задач:

218

| R(0)|< ∞, R(1) = 0.

а) R′′+

R′+ λR = 0,

0 ≤ r <1,

б) T ′ + λT = 0.

Решаем задачу (а).

Общее решение уравнения R′′+

R′+ λR

= 0 имеет вид

R(r)

( λr),

= AJ 0 ( λr)+ BY0

где

Y0 − функции

Бесселя и

Неймана. Поскольку

| R(0)|< ∞,

а Y0 (r)→ ∞ при r → 0, полагаем

B = 0.

Используя граничное условие R(1) = 0, получаем

(μn r),

n =1,2,...,

λn = μn

= An J 0

гдеμn — нули функции Бесселя J0 (x), т.е.

J0 (μn ) = 0,

n =1,2,...

Решаем задачу (б). При λ = λn = μn2 имеем

T ′+ μn2T = 0.

Общее решение этого уравнения есть

(t)= B e−μn2 t .

6. Итак, вспомогательные решения уравнения (11) имеют вид

(μ

r)e

−μ

= A J

(μ

r)e

−μ2t

(r, z) = A B

где

An = An Bn — постоянные, которые предстоит найти.

7. Решение u(r,t) ищем в виде

∞

(μn r)e−μn2t .

u(r,t) = ∑υn (r,t) = ∑An J0

(12)

n=1

Эта функция является решением уравнения (11) и удовлетворяет граничному условию (9) при любых An , при которых

ряд (12) сходится. Eгo можно дважды дифференцировать по-

членно.

219

8. Находим An , при которых u(r,t) удовлетворяет на-

чальному условию (8).

Пологая в (12) t = 0, получаем

∞

(μn r) =1 − r 2 .

u(r,0) = ∑An J0

n=1

Отсюда в силу формул Эйлера-Фурье следует, что

A =

2∫(1 − r 2 )J0 (μn r)rdr

4J 2 (μn )

, n =1,2,...

J12 (μn )

μn2 J12 (μn )

Подставляя эти коэффициенты в формулу (12), получаем

∞

4J 2 (μn )

u(r,t) = ∑

e−μn2t J 0 (μn r).

2 2

n=1

μn

J1 (μn )

∞

4J2

(μn )

Ответ. u(r,t)= ∑

e−μn2

t J0 (μn r).

n=1

μn J1 (μn )

20. Задача Коши для уравнения теплопроводности

на прямой

Постановка задачи. Решить задачу Коши для уравнения

теплопроводности на прямой:

ut = a2

uxx ,

x (− ∞,+∞),

t (0,+∞),

(1)

u(x,0)= e−α x 2 +β x ,

x (− ∞,+∞).

(2)

План решения. Решение задачи Коши для уравнения теплопроводности на прямой определяется формулой Пуассона:

	1 2	+∫∞ e−	(x−ξ )2
u(x,t)=
u(x,t)=			4a 2 t	e−α ξ 2 +β ξ dξ.	(3)
2	πa	t −∞

Таким образом, задача сводится к вычислению интеграла (3). 1. Делаем замену переменной в интеграле (3):

ξ − x = y. 2 a2t

220

Получаем

u(x,t) =	1	+∞ 2			2 2		2
u(x,t) =	1	∫e	−y				dy.
			−y	−α	2 a t y+x	+β 2 a t y+x
	π −∞
2. Выделяя полный квадрат в выражении
	− y 2 −α(2 a2t y + x)2 + β(2 a2t y + x)
и используя равенство
					+∞
					∫e−u2 du =		π ,
					−∞
находим искомое решение							2t (2α x+β )2
					1	α	2t (2α x+β )2	2	+β x
	u(x, t)=						−α x		+β x
	u(x, t)=					e 1+4α a 2 t
				1 + 4αa2t

и записываем ответ.

Пример. Решить задачу Коши для уравнения теплопро-

водности
ut = uxx , x (− ∞,+∞), t (0,+∞),	(4)
u(x,0) = e−x x (− ∞,+∞).	(5)

Решение.

Решение задачи Коши для уравнения теплопроводности на прямой определяется формулой Пуассона (3). При a =1, α = 0 и β = −1 имеем

u(x,t) =	1	+∞	−	(x−ξ )2
u(x,t) =	1	∫e	−	4t e−ξ dξ.	(6)
2	πt −∞

Таким образом, задача сводится к вычислению интеграла (6). 1. Делаем замену переменной в интеграле (6):

ξ − x	= y,	dξ	= dy, ξ = 2 t y + x.
4t		4t
Получаем
u(x,t) =		1	+∞
u(x,t) =		1	∫e−y2 e−2 t y−x dy.
		π	−∞

2. Выделяя полный квадрат в выражении
получаем	− y2 − 2 t y − x = −(y + t )2 + t − x,

u(x,t)=	1	+∞	(y + t )2 et −xdy = et −x	+∞
		∫ e−		∫e−(y + t )2 dy = et −x .
	π	−∞	π	−∞
Ответ. u(x,t) = et−x .

222

221

VI. Использование MatLab для решения дифференциальных уравнений с частными производными

1. Численные методы решения дифференциальных уравнений с частными производными

В данном разделе кратко отметим общие сведения и классификацию уравнений с частными производными (УЧП), рассмотрим явные и неявные разностные схемы для эллиптических, параболических и гиперболических уравнений и их программные реализации, а также продемонстрируем основные идеи использования метода Монте-Карло для решения УЧП.

1.1. Общие сведения и классификация уравнений с частными производными

Определение 1. Дифференциальные уравнения, содержащие частные производные, называются дифференциальными уравнениями в частных производных. В отличие от обыкновенных дифференциальных уравнений (ОДУ), в которых неизвестная функция зависит только от одной переменной, в уравнениях с частными производными неизвестная функция зависит от нескольких переменных (например, температура зависит от координаты х и времени t). Для упрощения записи будем использовать следующие обозначения:

u		≡	∂u	,	S(t),	u	∂2 u
	t		∂t				xx ∂x 2

Примеры уравнений с частными производными:

•ut = uxx (одномерное уравнение теплопроводности);

•ut = uxx + u yy (двумерное уравнение теплопроводности);

223

•urr + 1r ur + r12 uθθ = 0 (уравнение Лапласа в полярных

координатах);

• utt = uxx + u yy + uzz (трехмерное волновое уравнение);

•utt = uxx + αut + βu (телеграфное уравнение).

Отметим, что в приведенных ранее примерах неизвестная функция и зависит более чем от одной переменной. Функция и, от которой находятся производные, называется зависимой переменной, переменные I, х, по которым производится дифференцирование, называются независимыми переменными. Методы решения уравнений в частных производных:

•метод разделения переменных

•метод интегральных преобразований

•метод преобразования координат

•метод преобразования зависимой переменной

•численные методы

•метод теории возмущений

•метод функций Грина

•метод интегральных уравнений

•вариационные методы

•метод разложения по собственным функциям

•метод обратной задачи рассеяния

Важность классификации УПЧ обусловлена тем что, для каждого класса существует своя общая теория и методы решения уравнений. Уравнения в частных производных (УЧП) можно классифицировать по многим признакам.

Методы классификации УЧП:

1. По порядку уравнения (порядком уравнения называют наивысший порядок частных производных, входящих в уравнение):

•ut = ux (уравнение первого порядка);

•ut = uxx (уравнение второго порядка);

224

•ut = uuxxx + sin x (уравнение третьего порядка);

2.По числу переменных (числом переменных называют число независимых переменных).

•ut = uxx (уравнение с двумя переменными)

• ut = urr + 1r ur + r12 uθθ (уравнение с тремя переменными

r, θ, t)

3. По критерию линейное/нелинейное.

Линейным уравнением второго порядка с двумя независимыми переменными называется уравнение вида

Auxx	+ Buxy + Cu yy + Dux + Eu y + Fu = G ,	(1)
где А, В, С, D, Е, F и G константы или заданные функции пере-
менных х и у.
•	uxx + yu yy = 0 , utt = e−t uxx + sin t (линейные уравнения);
•	uuxx + ut = 0 , xux + yu y + u2 = 0 (нелинейные

уравнения).

4. По критерию однородное/неоднородное.

Уравнение (1) называется однородным, если правая часть С(х,у) тождественно равна нулю для всех х и у. Если С(х,у) не равна нулю тождественно, то уравнение называется неоднородным. 5. По виду коэффициентов.

Если коэффициенты А,В,С,D,Е,F и G уравнения (1) — константы, то уравнение (1) называется уравнением с

постоянными коэффициентами, в противном случае уравнением с переменными коэффициентами.

Существует несколько типов линейных уравнений. Параболический тип. Уравнения параболического типа описывают процессы теплопроводности и диффузии и определяются условием

B2 − 4AC = 0.

225

Гиперболический тип. Уравнения гиперболического типа описывают колебательные системы и волновые движения и определяются условием

B2 − 4AC > 0.

Эллиптический тип. Уравнения эллиптического типа описывают установившиеся процессы и определяются условием

B2 − 4AC < 0.

Примеры линейных уравнений разных типов:

•ut = uxx , B2 − 4AC = 0 (параболическое);

• utt = uxx , B 2 − 4AC = 4 (гиперболическое);

•uξη = 0, B2 − 4AC =1 (гиперболическое);

• uxx + u yy = 0, B2 − 4AC = −4 (эллиптическое);

• yuxx + u yy = 0, B 2 − 4AC = −4 y (эллиптическое при y > 0, параболическое при y = 0, гиперболическое при y < 0).

1.2. Численные методы решения эллиптических уравнений

При решении эллиптических УЧП ставится задача отыскания решения в некоторой области пространства при заданных значениях функции на границе области (задача Дирихле). Иллюстрацией задачи Дирихле является задача нахождения решения уравнения Лапласа

u	rr	+	1	u	r	+	1	u	θθ	= 0, 0 < r <1,
							r 2
			r

с заданными граничными условиями (ГУ) u(1,θ) =sinθ, 0 ≤θ ≤ 2π.

Рассмотрение численных методов решения задачи Дирихле уравнения Лапласа

uxx + u yy = 0 ,

226

в прямоугольной области 0 ≤ x ≤1, 0 ≤ y ≤1	с граничными
условиями
u(x,0) = g1 ( y), u(1, y) = g2 ( y), u(x,1) = g3 ( y),	u(0, y) = g4 ( y),

начнем со знакомства с понятием конечно-разностная частная производная.

Напомним, что при численном интегрировании производную функции, определяемую в соответствие с выражением

′		f (x + h) − f (x)
f (x) = lim				,
		h
h→0
мы заменяем выражением	f	(x + h) − f (x)
′				(2)
f (x)			,
		h

с точностью до членов порядка А аппроксимирующей производную в точке х.

Выражение, стоящее в правой части (2), называется правой разностной производной.

В разложении Тейлора функции f(x) можно заменить h на -h и получить левую разностную производную:

′	f (x) − F (x − h)		(3)
f (x)		.
f (x)	h	.
	h

Складывая (2) и (3), получаем центральную разностную производную:

′	f (x + h) −	f (x − h)		(4)
f (x)			.
f (x)	2h		.
	2h

Поступая аналогично, можно получить центральную разностную производную — аппроксимацию второй производной:

′′	1	[ f (x + h) − 2 f (x) + f (x + h)].	(5)

f (x) h 2

Теперь можно распространить понятие конечно-разностной аппроксимации на частные производные. Используя разложение функции двух переменных в ряд Тэйлора

227

u(x + h, y) = u(x, y) + ux (x, y)h + uxx (x, y) h2 +K, 2!

u(x − h, y) = u(x, y) − ux (x, y)h + uxx (x, y) h2 −K, 2!

находим выражения для конечно-разностной аппроксимации частных производных:

ux (x, y)			u(x + h, y) − u(x, y)	,
ux (x, y)			h	,
	1		h
uxx (x, y)	1	[u(x + h, y) − 2u(x, y) + u(x − h, y)],
uxx (x, y)	h 2	[u(x + h, y) − 2u(x, y) + u(x − h, y)],
	h 2		u(x, y + k) − u(x, y)
u y (x, y)			u(x, y + k) − u(x, y)		,
u y (x, y)			k		,
			k

u yy (x, y) h12 [u(x, y + k) − 2u(x, y) + u(x, y − k)].

В данных формулах частные производные аппроксимируются правыми, центральными и левыми разностями, но мы далее будем использовать центральные разностные аппроксимации. Построим на плоскости (х, у) равномерную сетку (рис. 21). Будем использовать следующие обозначения:

u(x j , yi ) = uij , u(x j , yi + k) = ui+1, j , u(x j , yi − k) = ui−1, j , u(x j − h, yi ) = uij−1 , u(x j + h, yi ) = uij+1 ,

ux (x j , yi ) = 21h (ui, j+1 − ui, j−1 ), u y (x j , yi ) = 21h (ui+1, j − ui−1, j ),

uxx (x j , yi ) = h12 (ui, j+1 − 2ui, j + ui, j−1 ),

228

u yy (x j , yi ) = k12 (ui+1, j − 2ui, j + ui−1, j ).

Рис. 21. Координатная сетка, используемая для решения УЧП эллиптического типа

Заменим частные производные в уравнении Лапласа их конечно-разностной аппроксимацией:

1		(ui, j+1 − 2ui, j−1 ) +			1	(ui+1, j − 2ui, j + ui−1, j ) = 0.	(6)
	h 2
					k 2
Если k=h, то уравнение Лапласа приводится к виду
		ui+1, j + ui−1, j + ui, j+1 + ui, j−1 − 4uij = 0.					(7)
Разрешив (10.7) относительно uij , получим
		uij =	1	(ui+1, j + ui−1, j + ui, j +1 + ui, j−1 ).			(8)

		4

Отметим, что в (8) все соотношения берутся для внутренних узлов сетки, так как значения функции на границе заданы. Соотношение (8) можно трактовать, как аппроксимацию

229

значения функции в точке (xi , y j ) средним значением

решения по четырем соседним точкам. На первый взгляд, польза от выражения (8) не очень очевидна, т. к. мы нашли связь между значением функции в ij-том узле и значениями

функции в соседних узлах: (ij −1) -ом, (ij +1) -ом, (i −1j) -ом, (i +1 j) -ом, которые в свою очередь также неизвестны. Однако

оказывается, что если задать некоторые начальные значения решения уравнения Лапласа в узлах сетки и затем их последовательно уточнять в соответствие с (8), то итерационный процесс будет сходиться (релаксировать) к точному решению.

Таким образом, численное решение задачи Дирихле методом релаксации находится в соответствие со следующим алгоритмом:

1. Присвоить величинам uij во внутренних узлах сетки

некоторые численные значения (например, равные среднему значению всех граничных условий).

2. Пересчитать значения во всех внутренних точках сетки в соответствии с (8) (заменяя старое значение средним значением, вычисленным по четырем соседним точкам).

Отметим, что при этом неважно, по строкам или по столбцам организован процесс счета. Недостатком данной схемы является низкая скорость сходимости итерационного процесса, которую, однако, можно улучшить, используя специальные методы, например метод верхней и нижней релаксации, основанные на методе Зейделя.

Пример 1. Найти в пакете МАТLАВ решение задачи Дирихле уравнения Лапласа

uxx + u yy = 0,

с граничными условиями

u(x,0) = 0, u(1, y) = g 2 ( y), u(x,1) = 0, u(0, y) = g4 ( y).

1. Создайте файл InterationL.m (листинг 1), содержащий описание функции, возвращающей численное решение

230

уравнения Лапласа методом релаксаций (для получения вычислительной схемы, обсуждение которой проводилось ранее, следует положить omega=1).

Листинг 1. Файл IterationL.m

function z=interationL(N,mega,Number_of_Interation,phi)

%функция, возвращающая значения потенциала на каждом шаге

%итерационного процесса

h=1/N; % шаг сетки

% вычисление координат узлов сетки i=1:N+1;

x(i)=(i-1)*h; j=1:N+1; y(j)=(j-1)*h;

% итерационный цикл

for k=1: Number_of_Iteration

% прохождение по узлам сетки for j=2:N

for i=2:N

phi (i,j)=(1-Omega)*phi (i,j)+Omega/4*(phi (i+1,j)+phi (i-1,j)+… phi (I,j+1)+phi (I,j-1)-h.^2*f(i+1j+1)); % релаксация

end;

end; if k=1 q=phi; else

q=cat (1,q,phi); end;

end;

z=q;

2. Выполните следующую последовательность команд:

N=15;

i=1:N+1;

j=1:N+1;

mu(i,1)=10; % потенциал по левой границе mu(i,N+1)= -10; % потенциал по правой границе mu(1,j)=5; % потенциал по нижней границе

mu(N+1,j)=5; % потенциал по верхней границе

%задание начального приближения kx=2:N;

ky=2:N;

mu(kx,ky)=12; % параметр релаксации

Omega=1;

Niter=200; % число итераций

z=interationL(N,Omega,Niter,mu); % решение уравнения Лапласа

%вычисление векторов и матриц для построения карты линий

%уровня x(i)=(i-1)/N; y(j)=(j-1)/N;

[x1 y1]=meshgrid(x,y);

K=100; % номер итерации для построения карты линий уровня

N1=(N+1)*K+1;

N2=(N+1)*(K+1);

A=z(1:N+1,N1:N2); % выделение К-го решения из общей % матрицы решений

[C,h]=contour(x1,y1,A,17); % построение карты

%эквипотенциальных поверхностей К-го решения уравнения %Лапласа (рис. 22)

232

231

Рис. 22. Карта линий равного потенциала численного решения уравнения Лапласа

Для просмотра процесса релаксации решения уравнения Лапласа следует выполнить следующую последовательность команд:

%последовательность команд для создания анимационного клипа set(gca,'nextplot','replacechildren'); % задание режима

%перерисовки карты

%в одном и том же окне

%создание кадров анимации клипа

for K=2:Niter-1 N1=(N+1)*(K-1)+1; N2=(N+1)*K; A=z(1:N+1,N1:N2); [C,h)=contour(x1,y1,A,17);

F(K-1)=getframe; % создание одного кадра end;

МАТLАВ, в процессе выполнения цикла по переменной к, выводит на экран каждый вновь создаваемый кадр. Для

233

повторного воспроизведения анимационного клипа используется команда movie (F,n), где F- имя переменной, в которую помещены кадры клипа, если значение n не указано, то клип воспроизводится бесконечное число раз (до закрытия графического окна). Для получения стоп-кадра следует щелкнуть по любому пункту меню графического окна. Для продолжения воспроизведения нужно щелкнуть мышью в поле графика. Можно сохранить созданный анимационный клип в файле, используя команду save). Например, для созданного ранее анимационного клипа данная команда имеет следующий синтаксис:

>>save имя_файла F

Для загрузки и выполнения ранее созданного анимационного клипа используется следующая последовательность команд:

>>load имя_файла имя_переменной >>movie (имя_переменной)

Рассмотрим решения краевой задачи двумерного уравнения Лапласа для квадратной области (0 ≤ х ≤ 1 см, 0 ≤ у ≤ 1 см) с известными потенциалами на границах (u(x,0) = 10, u(x,1) =-10, и(0,у) = 5, u(1,у) = 5), полученного на сетке, состоящей из 15x15 узлов (рис. 22). Из рис. 22 видно, что линии, расположенные на карте эквипотенциальных уровней оказываются негладкими (имеют в некоторых точках изломы). Наличие изломов, в свою очередь, у линий равных потенциалов свидетельствует о наличии разрывов у

производной функции ϕ(x, y) , описывающей напряженность электрического поля. С другой стороны, как известно из теории функций комплексной переменной, функцияϕ(x, y) ,

удовлетворяющая уравнению Лапласа, является аналитической. Необходимым и достаточным условием аналитичности функции ϕ(x, y) является непрерывность ее

234

производных. Этому, как очевидно, не отвечает полученное нами численное решение. Обнаруженный "дефект" численного решения связан с большим шагом сетки, на которой производится поиск решения уравнения Лапласа. Для его устранения можно использовать два способа:

1.находить численное решение на сетке с меньшим шагом;

2.используя найденное числовое решение на сетке, состоящей из 15x15 узлов, находить значения в точках, не совпадающих с узлами сетки, с помощью интерполяционной процедуры.

Для использования сплайн-интерполяции следует дополнить приведенную выше последовательность команд следующими командами:

% задание координатной сетки для вычисления значений сплайна

M=100;

n=1:M; x2(n)=(n-1)/M; y2(n)=(n-1)/M;

[X2 Y2]=meshgrid(x2,y2); zi3=interp2(x1,y1,A,X2,Y2,'splain'); %вычисление

%значений сплайна

[C,h]=contour(X2,Y2,zi3,17);

Результаты выполнения дополнительных команд представлены на рис. 23. Анализ карты эквипотенциальных поверхностей, представленных на рис. 22, 23, показывает, что, используя сплайн-интерполяцию, удалось устранить недостатки численного решения, проявляющиеся в наличии изломов линий равного потенциала.

235

Рис. 23. Карта линий уровня интерполированного решения уравнения Лапласа

1.3. Явные разностные схемы для уравнений параболического и эллиптического типов

Явные разностные схемы используются для решения уравнений, в которые входят производные по времени. Для решения данных задач используются явные разностные схемы, с которыми мы познакомимся на примере явной схемы бегущего счета для уравнения теплопроводности.

Рассмотрим решение смешанной краевой задачи для следующего УЧП:

ut =u xx , 0 < x <1, 0 < t < ∞,

(9)

с граничными условиями

u = (0, t) =1

, 0 < t < ∞ux (1, t) = −[u(1, t) − g(t)]

236

с начальными условиями

u(x,0) = 0, 0 ≤ x ≤1.

Рассматриваемое УПЧ описывает распределение температуры в стержне, начальная температура которого равна нулю. Левый конец стержня находится при постоянной температуре, на правом конце стержня происходит теплообмен с окружающей средой, температура которой определяется функцией g(t).

Для решения задачи методом конечных разностей построим прямоугольную сетку (рис. 24), узлы которой определяются формулами:

x j = jh, j = 0,1,2,K, n ,

ti = ik,i = 0,1,2,K, m.

Отметим, что значения м,-,- на левой и нижней сторонах сетки известны из начальных и граничных условий, на правой границе известно значение частной производной решения уравнения по переменной х.

Заменим частные производные в уравнении теплопроводности их конечно-разностными аппроксимациями:

		ut =	1	[u(x, t + k) − u(x, t)] =	1	[ui+1 j − uij ],
			k		k
	1						1
uxx =		[u(x + h, t) − 2u(x, t) + u(x − h, t)] =						[uij−1 − 2uij + uij−1 ].
	h 2						h 2

237

Рис. 24. Пространственно-временная сетка, используемая для решения одномерного уравнения теплопроводности

Подставим данные выражения в исходное уравнение ut = uxx

и разрешим получившееся уравнение относительно значений функции на верхнем временном слое. В результате получаем:

ui=1 j = uij	k	[uij+1 − 2uij + uij−1 ].	(10)
	h 2

Формула (10) решает поставленную задачу, поскольку она выражает решение в данный момент времени через решение в предыдущий момент времени.

Для решения смешенной краевой задачи необходимо аппроксимировать производную в граничном условии на правом конце:

ux (1, t) = −[u(1, t) − g(t)].

Используя конечно-разностную аппроксимацию, получаем:

Из (11) находим:

uin =	uin−1 − hgi	.	(12)

	1 + h

Формулы (10), (12) позволяют начать вычисления по явной схеме.

Алгоритм вычислений по явной схеме реализуется следующей последовательностью действий:

1. Находим решение на сеточном слое t = t , используя явную формулу:

u2 j = u1 j +	k	[u1 j+1 − 2u1 j + u1 j−1 ], j = 2,3,K, n −1	(13)
	h2

2. Находим величину u2n по формуле (12):

u2,n =	u2,n−1 +hg2	.		(14)

	1 + h		t = t .
Завершив шаги 1, 2, получаем решение при				Для
получения решения при t = 2 t повторяют			шаги	1,2,

поднявшись на одну строку вверх, т.е. увеличив i на единицу и используя uij с предыдущей строки. Аналогично вычисляется

решение в последующие моменты времени t = 3 t,4 t,K

У явной схемы имеется один существенный недостаток: если шаг по времени оказывается достаточно большим по сравнению с шагом по х, то погрешности округления могут стать настолько большими, что полученное решение теряет смысл, т. е. решение становится неустойчивым. Можно показать, что для применимости явной схемы должно

выполняться условие k / h 2 ≤ 0.5.

Пример 2. Найти в пакете МАТLАВ решение краевой задачи уравнения теплопроводности (10.8) с начальными условиями:

0, если х ≠ 25

T (x,0) = 1,еслих = 25 ,

где x [1, 50], и граничными239условиями:

T (t,1) = 0, T(t,50) = 0 ,

на временном интервале [0, 49]. Решение:

>>Nt=50; % число шагов по времени >>Nx=50; % Число узлов координатной сетки

>>t=1:Nt;

>>x=1:Nx;

% задание начальных и граничных условий

>>f(1,x)=0;

>>f(t,1)=0;

>>f(t,Nx)=0;

>>f(1,25)=1;

%вычисление решения в последовательные моменты времени в

%соотношении с (10.10)

>>for t=2:Nt for x=2:Nx-1

f(t,x)=f(t-1,x)+0.15*(f(t-1,x-1)-2*f(t-1,x)+f(t-1,x+1)); end;

end;

>>surf(f) % визуализация численного решения (рис. 25)

Рис. 25. Численное решение уравнения теплопроводности

240

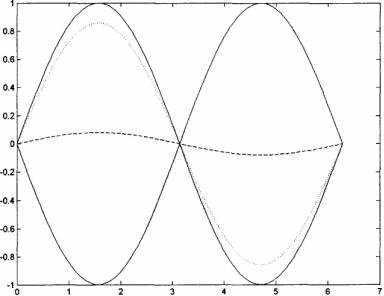
Получим явную вычислительную схему для нахождения численного решения УЧП гиперболического типа, на примере волнового уравнения:

∂2U

(15)

∂2 x

ν 2

∂t 2

Запишем уравнение (15) в конечных разностях:

uij+1 − 2uij + uij−1

ui+1 j

− 2uij + ui−1 j

(16)

ν 2

τ 2

Полученное уравнение позволяет выразить значение функции

и в момент времени ti+1				через значения функции в предыдущие
моменты времени:
ui +1 j =ν	2		τ	2	(uij+1 − 2uij + uij−1 )+ 2uij − ui−1 j .	(17)
ui +1 j =ν					(uij+1 − 2uij + uij−1 )+ 2uij − ui−1 j .	(17)
		h

Разностная схема (17) устойчива, если τ ≤ h /ν .

Отметим, что для начала вычислений в соответствии с (17) необходимо знать значения функции в моменты времени t0 и

t1 . Данное обстоятельство обусловлено тем, что мы решаем уравнение второго порядка по времени. Для нахождения решений в моменты времени t0 и t1 необходимо использовать,

например, начальное условие для первых производных функции u (рис. 26).

241

Рис. 26. Решениеволновогоуравнениявмоментывремениt=0, 9, 24, 49

Пример 3. Найти в пакете МАТLАВ решение краевой задачи волнового уравнения (14), в котором ν =1,с начальными условиями:

U(x,0) =sin(x),

где x [0, 2π], и граничными условиями:

U (0, t) = 0, U(2π,t) = 0

на временном интервале [0,59].

Решение:

>>Nt=60; % число шагов по времени >>Nx=100; % число узлов по координате % задание начальных и граничных условий

>>U(1,j)=sin(2*pi*(j-1)/(Nx-1); % начальное условие

>>U(2,j)=U(1,j); % граничное условие

>>a=1;k=1;

>>for i=2:Nt

242

for j=2:Nx-1

U(i+1,j)=a.^2*k*(U(i,j+1)-2*U(i,j)+U(I,j-1))+2*U(I,j)-U(i-1,j); end;

end;

% визуализация решений уравнения в выбранные моменты времени

>>j=1:Nx; >>plot(2*pi*(j-1)/(Nx-1),U(1,j)) >>hold on >>plot(2*pi*(j-1)/(Nx-1),U(10,j),':') >>plot(2*pi*(j-1)/(Nx-1),U(25,j),'--') >>plot(2*pi*(j-1)/(Nx-1),U(50,j),'-')

1.4. Неявная разностная схема для уравнения параболического типа

Построим неявную разностную схему для уравнения теплопроводности. Рассмотрим задачу нахождения решения УЧП

ut = uxx , 0 < x <1, 0 < t < ∞,		(18)
с граничными условиями
u(0, t) = 0	0 < t < ∞,
	0 < t < ∞,
u(1,t) = 0,
и начальными условиями
u(x,0) =1,	0 ≤ x ≤1.

Воспользуемся следующими конечно-разностными аппроксимациями частных производных ut и uxx :

ut (x, t) = k1 [u(x, t + k) − u(x, t)],

uxx (x, t) = hλ2 [u(x + h, t + k) − 2u(x, t + k) + u(x − h, t + k)] +

+ 1h−2λ [u(x + h, t) − 2u(x, t) + u(x − h, t),

где λ – выбирается из отрезка [0,1].

243

Отметим, что uxx аппроксимируется взвешенным средним

центральных разностных производных в момент времени t и (t+k). При λ = 0.5 получаем обычное среднее двух центральных производных, при λ = 0 получаем обычную явную схему, о которой упоминалось ранее.

После замены частных производных ut , uxx в задаче (18) получаем разностную задачу:

1	(ui+1, j −ui, j ) =	λ	(ui+1 j+1 − 2ui+1 j		+ ui+1, j−1 ) +	1 −λ	(uij+1 − 2uij + uij−1 ),
k	(ui+1, j −ui, j ) =	h2	(ui+1 j+1 − 2ui+1 j		+ ui+1, j−1 ) +	h2	(uij+1 − 2uij + uij−1 ),
k		h2	ui,1	= 0,		h2
			ui,1	= 0,	i =1,2,K, m,		(19)
					i =1,2,K, m,		(19)
			ui,n = 0,
			u1 j =1,	j =1,2,K, n −1.

Перенесем все неизвестные значения и с верхнего временного слоя (с индексом (i+ 1)) в левую часть уравнения:

	− λrui + j+1 + (1 + 2rλ)ui+1, j−1 =			(20)
	= r(1 − λ)ui, j+1 + [1 − 2r(1 − λ)]uij + r(1 − λ)uij−1 ,			(20)
	= r(1 − λ)ui, j+1 + [1 − 2r(1 − λ)]uij + r(1 − λ)uij−1 ,
где r = k / h2 .
	Схема уравнения системы (20)			Таблица 1
				Таблица 1

	j − 1	j		j + 1
i + 1	− rλ	+ 1 + 1rλ	+ − rλ
i	r(1 − λ)	+ 1 − 2rλ(1 − λ)	+ r(1 − λ)

Если i фиксировано, а j изменяется от 2 до (n-1), соотношения (20) определяют систему (n-2) уравнений с (n-2) неизвестными ui+1,2 , ui+1,3 , ui+1,4 ,K, ui+1,n−1 , которые являются решением задачи во внутренних узлах сетки на временном слое t=(i+1)∆t.

Наглядное представление о структуре каждого уравнения (20) дает таблица 1.

Обсудим более подробно алгоритм решения смешанной краевой задачи одномерного уравнения теплопроводности для

244

случаев λ= 0.5 (схема Кранка-Никольсона), h=∆=0.2, k=∆t = 0.08 (при этом r = k/h2=2). В данном случае сетка содержит 6 узлов вдоль оси х. В соответствии с вычислительной схемой (20), двигаясь слева направо j = 2, 3, 4, 5 по первым двум слоям (j=1), получаем следующие четыре уравнения:

− u21 + 3u22 − u23 = u11 − u12 + u13 =1, − u22 + 3u23 − u24 = u12 − u13 + u14 =1, − u23 + 3u24 − u25 = u13 − u14 + u15 =1,

− u24 + 3u25 − u26 = u14 − u15 + u16 =1.

Перепишем уравнения в матричной форме:

3		−1	0	0	u	22	1

−1		3	−1	0	u23		= 1 .
	0	−1	3	−1	u	24	1
	0	0	−1	3
	0	0	−1	3	u25		1

Матрица данной системы называется трехдиагональной. В наиболее общем виде трехдиагональная система имеет вид:

b		c		0	0
	1		1	c2	0
a1		b2
0		a2		b3	c3
		.		. .
.
.		.		. .
		.		. .
.
		.		. .
.

.	. . .	0	x1	d1
.	. . .	0
.	. . .	0	x2	d 2
.	. . .	0	x3	d3
.	. . .	.				(21)
.	. . .	.	.	= .	.	(21)
.	. . .	.	.	.
.	. . .
.	. . .	cn−1	.	.
.
.	. . an−1 bn		xn	d n

Для нахождения ее решения преобразуем систему к эквивалентному виду:

245


1	c1
	1
0	1
0	0

	.
.	.
	.
.	.
.	.
	.
.	.

где

0	0 . . . .								0					x	1	d1
c2														x	1
c2	0 . . . .								0					x	2	d 2
1	c . . . .								0							d
1	c . . . .								0					x		d
. .		3								.					3		3		(22)
. .		. . . .								.				.		= .		,	(22)
. .		. . . .								.
. .		. . . .								.				.		.
. .		. . . .							cn−1
. .		. . . .							cn−1					.		.
. .		. .			. an−1 bn
. .		. .			. an−1 bn									xn		d n

		c		= c			1		/ b ,
			1				1		1
c	=	c j+1				,			j =1,2,K, n − 2 ,
c	=	b j+1 − a j c j				,			j =1,2,K, n − 2 ,
j+1		b j+1 − a j c j
		d			= d			1	/ b ,
			1					1	1
					d	j+1			− a	j	d
		d	=			j+1				j		j	.
		d	=		b j+1 − a j c j								.
		j+1			b j+1 − a j c j

Решение системы (22) находится последовательно снизу вверх. Для нахождения решения на следующем шаге во времени следует вновь решить аналогичную систему. Отметим, что объем вычислений на каждом шаге больше, чем в явной схеме, но хорошую точность удается получить даже при гораздо большем шаге.

Предваряя решение смешанной краевой задачи, запишем в явном виде систему линейных уравнений для схемы с λ = 1:

1+		2r	−r
	−r		1+ 2r	−r
	−r		1+ 2r	−r
			O	O	O
			O	O	O
				r	1+2r
				r	1+2r
					− r
					− r

	ui+1,2

	u	i+1,3
		i+1,3
		M


−r ui+1,n−2
1+2r
1+2r	u	i+1,n−1
		i+1,n−1

	u	i,1
		i,1


	=



	ui,n

+ r ui,1

ui,2

ui,n−2

−1 + r ui,n

, (22’)

246

где ui,1 = и(t,0), ui,n = и(t,1), которую будем использовать далее

при решении смешанной краевой задачи для уравнения параболического вида.

Пример 4. Найти в пакете МАTLАВ решение смешанной краевой задачи УЧП

ut = uxx ,

с начальными условиями

u(0, x) =sin(πx) + x, 0 ≤ x ≤1,

и граничными условиями

u(t,0) = 0, u(t,1) =1

с использованием неявной разности схемы (λ=1).

Для нахождения решения смешанной краевой задачи необходимо:

1. Создать файл U1.m (листинг 2), содержащий описание функции, возвращающей значения решения смешанной краевой задачи.

Листинг 2. Файл U1.m function z=U1(u,A,r,Nt,Nx)

%u - матрица, содержащая начальные и граничные условия

%А – матрица системы (22)

%r=k/h2 – переменная, введенная в (20)

%Nt – число шагов по времени

%Nx – число узлов по координате

z=u; u1=u(1:1,2:Nx-1); for i=1:Nt-1 a=r*z(i,1); b=r*z(i, Nx); u1(1,1)=u1(1,1)+a;

u1(1,Nx-2)=u1(1,Nx-2)+b; u2=A^-1*u1';

u1=u2';

for j=2:Nx-1 z(i+1,j)=u2(j-1,1);

end;

247

end;

2. Выполнить следующую последовательность команд:

>>Nx=30; % число узлов по координате х

>>Nt=100; % число шагов по времени % задание начальных условий

>>j=1:Nx;

>>u(1,j)=sin(pi*(j-1)/(Nx-1))+(j-1)/(Nx-1);

% задание граничных условий

>>alpha=0;

>>beta=1;

>>i=1:Nt;

>>u(i,1)=alpha;

>>u(i,Nx)=beta;

% создание матрицы системы линейных уравнений (22)

>>r=5;

>>for k=1:Nx-2 A(k,k)=1+2*r;

end;

>> for m=2:Nx-2 A(m-1,m)=-r; A(m,m-1)=-r;

end;

>>z=U1(u,A,r,Nt,Nx); % вычисление решения системы смешанной краевой задачи

>>surf(z); view(160,70); colormap gray

% визуализации решения смешанной краевой задачи (рис. 27)

Завершая обсуждение разностных методов решения дифференциальных уравнений в частных производных, отметим, что различные методы и средства для решения данного типа уравнений пакета МАТLАВ объединены в специализированный пакет Partial Differential Equations Toolboox (РDЕ Тool-bоох), подробное обсуждение которого выходит за рамки нашего курса. Заинтересованный читатель может изучить приемы работы с РDЕ Тооlbоох, ознакомившись с руководством пользователя, которое входит

248

в состав документации, поставляемой в электронной форме	1. Блуждания пьяницы начинаются из произвольной точки
вместе с пакетом МАТLАВ (файл РDЕ.pdf).	сетки (в нашем случае это точка А (рис. 28)).

Рис. 27. Решение смешанной краевой задачи УЧП параболического типа

1.5. Решение уравнений с частными производными методом Монте-Карло

Рассмотрим решение задачи Дирихле уравнения Лапласа методом случайных блужданий:

uxx + u yy = 0, 0 < х < 1, 0 < у < 1.

Для иллюстрации метода Монте-Карло рассмотрим игру, которая называется "Блуждающий пьяница".

Правила игры:

249

Рис. 28. Координатная сетка, используемая в методе Монте-Карло

2.На каждом шаге пьяница случайным образом перемещается в одну из четырех соседних точек сетки (в нашем случае — одна из точек С, В, D, Е). Вероятность попадания в каждую из точек равна.

3.После перехода в соседнюю точку процесс блуждания возобновляется. Перемещения пьяного продолжаются до тех

пор, пока он не достигнет одной из граничных точек Pi. Номер граничной точки фиксируется, и на этом случайная прогулка заканчивается.

4.Производим повторение шагов 1-3 достаточное количество раз и определяем количество посещений пьяным каждой граничной точки. Отношение числа посещений пьяным каждой точки границы к полному числу испытаний определяет вероятность попадания пьяного в данную точку границы.

5.Предположим, что пьяница получает вознаграждение gi, если он достигает точки pi , и предположим, что цель игры —

250

вычислить среднее вознаграждение R(А) для всех случайных прогулок, начинающихся из точки А. Тогда искомый средний выигрыш определяется формулой:

R( A) = g1 PA ( p1 ) + g2 PA ( p2 ) +K+ g12 PA ( p12 ). (23)

Для чего надо играть в "Блуждающего пьяницу"? Оказывается, что среднее вознаграждение (23) является решением задачи Дирихле в точке А. Данный вывод основан на двух фактах.

1. Предположим, что пьяница начал свое движение из точки, лежащей на границе. Каждая такая прогулка заканчивается в той же точке, и пьяница немедленно получает вознаграждение gi . Таким образом, среднее вознаграждение для каждой точки равно gi . 2. Теперь предположим, что прогулка начинается из внутренней точки. Тогда ясно, что среднее вознаграждение для точки К(А) будет средним арифметическим от средних вознаграждений для четырех соседних точек:

R( A) =	1	[R(B) + R(C) + R(D) + R(E)].	(24)
	4

Итак, мы видим, что R(А) удовлетворяет уравнению (24) в каждой внутренней точке и равно gi в граничной точке. Если gi — это значения функции g(х,у) из граничного условия в граничных точках pi , то два наших уравнения точно совпадают с двумя уравнениями, которые получены при решении задачи Дирихле методом конечных разностей. То есть величина R(А) соответствует величине uij в разностных уравнениях

uij	=	1	[ui−1 j + ui+1 j + uij−1 + ui, j+1 ],	(25)
uij	=	4	[ui−1 j + ui+1 j + uij−1 + ui, j+1 ],	(25)
		4
где (i, j) – внутренняя точка,
			uij = gij ,	(26)

где gij – значение решения в граничной точке (i, j).

Таким образом, величина R(А) действительно аппроксимирует решение уравнения с частными производными в точке А .

Пример 5. Решение методом случайных блужданий в пакете МАТLАВ уравнения Лапласа:

uxx + u yy = 0, 0 < x <1, 0 < y <1, u(0, y) = 0,u(1, y) = 0, 251u(x,0) =5,u(x,1) = 0.

1. Создайте файл Моntе_Каг1о.m (листинг 3), содержащий описание функции, возвращающей численное решение уравнения Лапласа.

Листинг 3. Файл Monte_Carlo.m

function z=Monte_Carlo(Nx,Ny,NTrial,XL,XR,Yu,Yd) for j=1:Nx

U(1,j)=Yd(j);

U(Ny,j)=Yu(j);

end;

for i=1:Ny U(i,1)=XL(i); U(i,Ny)=XR(i); end;

for i=2:Nx-1 for j=2:Ny-2 Xs=j;

Ys=I;

for m=1:Nx VL(m)=0; VR(m)=0; end;

for m=1:Ny Gd(m)=0; Gu(m)=0; end;

for k=1:NTrial x=Xs;

y=Ys;

while not (==1)&not(x==Nx)&not(y==1)&not(y==Ny) R=rand(1,1);

if R<0.25 x=x-1; end;

if (0.25<=R)&(R<0.5)

x=x+1;

end;

if (0.5<=R)&(R<0.75) 252 y=y-1;

end;

if (0.75<=R)&(R<=1) y=y+1;

end;

if x==1 VL(y)=VL(y)+1; end;

if x==Nx VR(y)=VR(y)+1; end;

if y==1 Gd(x)=Gd(x)+1; end;

if y==Ny Gu(x)=Gu(x)+1; end;

end;

s1=0;

for m=2:Nx-1 s1=s1+Gd(m)*U(1,m)+Gu(m)*U(Ny,m); end;

s2=0;

for m=2:Ny s2=s2+VL(m)*U(m,1)+VR(m)*U(m,Nx); end;

U(I,j)=(s1+s2)/NTrial;

end;

z=U;

Рис. 29. Карта линий уровня решения уравнения Лапласа, полученного методом Монте-Карло

2. Далее необходимо выполнить следующую последовательность команд:

% задание числа узлов координатной сетки

>>Nx=14;

>>Ny=14;

% задание граничных условий

>>i=1:Nx;

>>j=1:Ny;

>>XL(i)=5;

>>Yu(j)=0;

>>XR(i)=5;

>>Yd(j)=0;

% нахождение численного решения

>> U=Monte-Carlo(Nx,Ny,XL,XR,Yu,Yd); >>contour(U,17)% визуализация численного решения (рис. 29)

254

253

Для сравнения на рис 30 представлено решение уравнения Лапласа, полученное методом релаксаций.

Рис. 30. Решение уравнения Лапласа, полученное методом релаксаций

Рассмотрим эллиптическую краевую задачу в квадрате uxx + (sin x)uxx = 0, 0 < x <π, 0 < x <π,

u(x, y) = g(x, y)

на его границе.

Для того чтобы решить эту задачу, заменим uxx , uyy и sinx следующим образом:

uxx = uij+1 − 2uij + uij−1 , u yy = ui+1 j − 2uij + ui−1 j,

sin x = sin x j .

Подставим эту замену в уравнение с частными производными. Разрешив получившееся уравнение относительно uij, получаем

uij =	uij+1 + ui, j−1 − sin x j (ui+1 j + ui−1 j )	.	(27)

	2(1 + sin x j )

Коэффициенты при ui+1j ,uij+1 ,uij-1 ,ui-1j в (27) положительны, и их сумма равна единице. Другими словами, решение uij

является взвешенным средним решением в четырех соседних точках.

Следовательно, можно модифицировать метод "Блуждающего пьяницы" так, чтобы вероятности перехода в соседние точки равнялись коэффициенту в соответствующем члене. Другими словами, если пьяница находится в точке (i, j), то он переходит в точку:


•	(i,j+1) c вероятностью	1				,
				2(1 + sin x j )
•	(i, j-1) с вероятностью	1				,
			2(1 + sin x j )
•	(i+1,j) с вероятностью			sin x j		,
			2(1 + sin x j )
•	(i-1,j) с вероятностью			sin x j
					,
		2(1 + sin x j )

В остальном правила игры не меняются. Модификация для других задач может оказаться более хитроумной, однако основная идея метода не меняется.

256

255

2. Численные методы решения интегральных уравнений

Отметим общие сведения и классификацию интегральных уравнений, рассмотрим квадратурные методы решения интегральных уравнений Фредгольма и Вольтерра и их программные реализации.

2.1. Общие сведения об интегральных уравнениях

Определение 1. Интегральным уравнением называется уравнение относительно неизвестной функции, содержащейся под знаком интеграла.

К интегральным уравнениям приводятся многие задачи, возникающие в математике и математической физике. Исторически первой задачей, сведенной к интегральному уравнению

z	ϕ(ξ)
∫	ϕ(ξ)	dξ = f (z),
0	z −ξ

считается задача Абеля, имеющая следующую формулировку. Определить вид кривой x =ϕ(z) , по которой в вертикальной

плоскости ХоZ под действием силы тяжести должна скатываться материальная точка, так чтобы, начав свое движение с нулевой начальной скоростью из точки z = z0 она

достигала оси оХ за заданное время T = f(z).

Интегральные уравнения широко используются в моделях, рассматриваемых в теории упругости, газовой динамике, электродинамике, экологии и других областях физики, в которых они являются следствием законов сохранения массы, импульса и энергии. Достоинство данных моделей состоит в том, что интегральные уравнения, в отличие от дифференциальных, не содержат производных искомой функции и, следовательно, жесткие ограничения на гладкость решения отсутствуют.

257

Приведем примеры интегральных уравнений:

1. Зависимости между напряжениями и деформациями в упруго-вязких материалах описываются уравнениями

	σ(t)		1	t
ε(t) =		+		∫K(t −τ)σ(τ)dτ,
	E		E
				0
				t

σ(t) = Eε(t) − E∫T (t −τ)ε(τ)dτ,

где Е — модуль упругости, K(t-τ) — функция влияния напряжения σ(t) в момент времени на деформацию ε(t) в момент времени t, Т(t-τ) — аналогичная функция влияния деформации.

2. Решение задачи об определении вида потенциальной энергии по периоду колебаний сводится к решению интегрального уравнения, где Е — энергия частицы, т— масса частицы, х1(Е), х2(Е) — координаты точки остановки, являющиеся решением уравнения

U(х) = Е.

Интегральное уравнение в достаточно общем виде можно представить в следующей форме:

x(t) = ∫K(t, s, x(s))ds + f (t)	(1)
D

где D — некоторая область n-мерного пространства, х — неизвестная функция, f — известная функция, К — функция относительно х (линейная или нелинейная).

Примечание. В общем случае функции х(t), f(t) — вектор-функции.

Далее мы ограничим повествование одномерными линейными интегральными уравнениями, в которых функция х(t) является функцией, зависящей от одной переменной, а область D — отрезком конечной длины. В этих уравнениях подынтегральная функция К(t,s,х(s)) представима в виде

Q(t,s)x(s).

Классификация типов линейных интегральных уравнений проводится по виду верхней границы интеграла в (1): если

258

верхняя граница интегрирования является постоянной, то уравнение называется уравнением Фредгольма, если переменной — уравнением Волыперра, которые, в свою очередь, подразделяются на уравнения первого и второго рода. На практике наиболее широко применяются линейные интегральные уравнения второго рода:

•Фредгольма

b
x(t) = λ∫Q(t, s)x(s)ds + f (t);	(2)

Рис. 31. Области задания ядер Q(t,s) интегральных уравнений Фредгольма (а) и Вольтера (б)

259

• Вольтерра

t
x(t) = λ∫Q(t, s)x(s)ds + f (t),	(3)

где f(t) — неизвестная функция, х(t) —решение уравнения, Q(t,s) — ядро интегрального уравнения.

Ядро интегрального уравнения Фредгольма определяется на множестве точек квадрата [а,b]×[а,b] (рис. 31а), уравнения Вольтерра — в треугольнике а≤а≤1≤b (рис. 316).

Уравнение Вольтерра можно считать уравнением Фредгольма, если доопределить его ядро Q(t,s) нулем в треугольнике а≤5≤t≤b. Тогда можно применять для его решения методы уравнения Фредгольма. Однако при этом могут быть упущены некоторые специфические особенности уравнения Вольтерра, что определяет необходимость их раздельного рассмотрения. Дополнительный множитель λ, который может быть отнесен к интегральному ядру, в (1), (2) введен для придания уравнениям более общего вида. Имеются теоремы, устанавливающие существование решений интегральных уравнений при различных значениях λ, которые доказываются подобно тому, как это делается в теории линейных дифференциальных уравнений, через рассмотрение соответствующих однородных уравнений (f(t) = 0).

Значительно более сложной задачей оказывается необходимость доказательства существования, единственности и непрерывной зависимости решений от функции f(t) для интегральных уравнений первого рода:

•Фредгольма

b
∫Q(t, s)x(s)ds = f (t);	(4)
a
• Вольтерра
t
∫Q(t, s)x(s)ds = f (t).	(5)

260

Эта задача относится к классу некорректных задач. Уравнения первого и второго рода можно записать в общем

виде, используя функцию h(1), тожественно равную нулю для уравнений первого рода и единице для уравнений второго рода:

h(t)x(t) = λ∫Q(t, s)x(s)ds + f (t).	(6)
D

Когда функция h(t) обращается в ноль в некоторых точках прямоугольника интегрирования, уравнение (6) относится к интегральным уравнения третьего рода. Уравнения данного типа встречаются в приложениях значительно реже, чем уравнения первых двух типов, и значительно менее изучены.

Многие используемые на практике интегральные уравнения имеют ядро, зависящее только от разности (t - s). Интегральные уравнения с данным типом ядра называются

уравнениями с разностным ядром. Примером таких уравнений является уравнение, получаемое в задаче Абеля.

Если Q(t,s) и f(t) — непрерывные функции, то при любых значениях параметра λ существует единственно непрерывное решение уравнения Вольтерра второго рода (5). Для уравнения Фредгольма второго рода (4) при тех же требованиях единственное непрерывное решение существует, например, при условии, что

λ	<	1	,	(7)
		C(b − a)

где C = max |Q(t, s) |.

t,s [a,b]

При снижении требований к гладкости возможных решений условие (7) ослабляется. Например, для функций, интегрируемых с квадратом, в роли достаточного условия фигурирует неравенство

261

\| λ \|<	1	.	(8)
\| λ \|<	b b	.	(8)
	b b
	∫∫Q2 (t, s)dtds
	a a

Известны формулы (или совокупности формул) позволяющие найти точное решение x(t). Например, решение уравнения Вольтерра с λ = 1 и мультипликативным ядром

Q(t, s) = p(t)s(t)		(9)
вычисляется по формуле
t
x(t) = ∫R(t, s) f (s)ds + f (t),		(10)
a
где
t
∫ p(ξ )q(ξ )dξ	.	(11)
R(t, s) = p(t)q(s)e s	.	(11)
Решение уравнения Фредгольма с вырожденным ядром
m
Q(t, s) = ∑pi (t)qi (s)		(12)
i=1
имеет вид
m
x(t) = λ∑zi pi (t) + f (t),		(13)

i=1

где числа zi — решения системы линейных алгебраических уравнений:

− λc z

−K− λc

= d

− λc21 z1 − λc22 z2

−K− λc2m zm = d2

(14)

− λsm1 z1 − λcm2 z2 −K− λcmm zm = dm

где cij = ∫qi (s) pi (s)ds, di = ∫qi (s) f (s)ds.

Условие существования и единственности решения уравнения Фредгольма с вырожденным ядром, как очевидно, зависит от

262

значения определителя D(λ) системы линейных алгебраических уравнений (14), называемого определителем Фредгольма. Если D(λ)≠0, то решение существует и единственно.

Наличие методов нахождения точного решения интегрального уравнения с вырожденным ядром позволяет построить приближенный метод, в основе которого лежит замена одного уравнения другим, ядро которого вырождено и в некотором смысле близко к ядру исходного уравнения. Данная замена ядра опирается на различные способы локальной аппроксимации функций, зависящих от двух переменных. Помимо упомянутого ранее метода замены ядра на вырожденное известен ряд других приближенноаналитических методов решения интегральных уравнений, например, метод последовательных приближений, метод моментов и др.

Далее мы рассмотрим численные методы решения интегральных уравнений, в основе которых лежит замена интеграла в интегральном уравнении конечной суммой, с помощью какой-либо квадратурной формулы. Это позволят свести решение исходной задачи к решению системы линейных алгебраических уравнений, число которых определяется числом узлов временной сетки. Методы решения интегральных уравнений, основанные на данном подходе,

называются квадратурными методами или методами конечных сумм. Преимущество данных методов состоит в простоте их реализации. Отметим, что без каких-либо изменений данные методы можно применять для решения нелинейных интегральных уравнений, имея в виду, что в этом случае приходится решать систему нелинейных алгебраических уравнений.

263

2.2. Квадратурный метод решения интегральных уравнений Фредгольма

Заменим определенный интеграл (4) его приближенным значением, вычисляемым с помощью конкретной квадратурной формулы

n
∫ϕ(s)ds ≈ ∑Ajϕ(s j ),	(15)

где j=1n — номера узлов сетки по переменной, Aj — весовые коэффициенты квадратурной формулы.

Подставив правую часть приближенного равенства (15) с ϕ(s) =Q(t, s) x(s) вместо интеграла в интегральное уравнение Фредгольма второго рода (4), получим

n
x(t) ≈ λ∑Aj Q(t, s j )x(s j ) + f (t).	(16)

j=1

Выражение (16) задает функцию, описывающую приближенное решение интегрального уравнения (4). Введем на отрезке [а, b] дискретную временную сетку t1 , t2,..., tn, узлы которой совпадают с узлами сетки s1, s2 ,..., sn. Для каждого момента времени tj выполняется равенство

n
x(ti ) ≈ λ∑Aj Q(ti , s j )x(s j ) + f (ti ).	(17)
j=1
где i = 1n.
Введем обозначения Qij = Q(ti , s j ), fi = f (ti ), xi = x(ti )	и

запишем (17) в виде системы n линейных алгебраических уравнений с n неизвестными:

(1 − λA1Q11 )x1 − λA2Q12 x1 −K− λAnQ1n xn = f1

− λA2Q21 )x1

− λA2Q22 x2 −K− λAn Q2n xn = f2

(1 − λA Q

− λA Q

−K− λA Q

= f

264

для решения которой можно использовать любой из методов, подробно обсуждавшихся ранее.

Таким образом, нахождение решения уравнения Фредгольма второго рода осуществляется в соответствие со следующим алгоритмом:

1.Задать временную сетку ti.

2.Вычислить значения функции f(t) в узлах временной сетки.

3.Вычислить элементы матрицы, составленной из коэффициентов системы линейных алгебраических уравнений.

4.Решить систему линейных уравнений.

Пример 1. Найти в пакете МАТLАВ решение интегрального уравнения

2	x(s)ds
x(t) = ∫	t + s	2	+ t +1 − t + 4 + t.
1	t + s

(Точное решение уравнения х(t) - t.)

1. Создайте файл q11.m (листинг 1), содержащий описание функции, возвращающей значения функции Q(t,s).

Листинг 1. Файл q11.m function z=Q(t,s) z=1./sqrt(t+s.^2)

2. Создайте файл f11.m (листинг 2), содержащий описание функции, возвращающей значения функции f(t).

Листинг 2. Файл f11.m function z=f11(t) z=sqrt(t+1)-sqrt(t+4)+t;

3. Создайте файл Solve_g11.m (листинг 3), содержащий описание функции, возвращающей решение интегрального уравнения.

Листинг 3. Файл Solve.m

function [X,Y]=solve_g11(x1,x2,N,Lambda)

% задание временной сетки h=(x2-x1)/(N-1); i=1:N; t(i)=x1+h*(i-1); s=t;

% задание коэффициентов квадратурной формулы метода трапеций

A(1)=0.5; m=2:N-1; A(m)=1; A(N)=0.5;

% вычисление значений функции Q(t,s) в узлах сетки for i=1:N

for j=1:N q(i,j)=Q11(t(i),s(j)); end;

end;

% вычисление значений функции f(t) в узлах временной сетки

F=f11(t); for i=1:N for j=1:N if i==j

M(i,j)=1-Lambda*A(i)*q(i,j)*h; else M(i,j)=-Lambda*A(i)*q(i,j)*h; end;

end;

X=t;

Y=M^-1*F'; % нахождение решения интегрального уравнения

4. Выполните следующую последовательность команд:

>>x1=1; % левая граница отрезка поиска решения

>>x2=2; % правая граница отрезка поиска решения

>>Lambda=1;

>>N=300; % число узлов разбиения отрезка

>>[N,X]=solve_g11(x1,x2,N,Lambda);

>>plot(X,Y) % визуализация решения интегрального уравнения

(рис.32)

265

266

Точность численного решения интегрального уравнения зависит от нескольких факторов: применяемой квадратурной формулы, числа узлов временной сетки, свойств функции Q(t,s). В ряде книг приводятся аналитические выражения, позволяющие оценить максимальную погрешность численного решения при использовании различных вычислительных схем. Однако эти оценки оказываются малопригодными из-за их громоздкости, поэтому на практике используют менее строгий метод контроля точности численного решения — принцип Рунге. Данный принцип заключается в сравнении численных решений, полученных на временных сетках с шагом 2h и h, в одних и тех же узлах временной сетки. Абсолютное значение разности этих решений характеризует величину погрешности численного решения. Недостаток настоящего подхода состоит в том, что при данном способе контроля приходится ограничиваться квадратурными формулами, пригодными только для сеток с равномерным шагом.

Рис. 32. Численное решение интегрального уравнения

2	x(s)ds
x(t) = ∫	t + s	2	+ t +1 − t + 4 + t.
1	t + s

Важно понимать, что необходимо согласовывать выбор конкретной квадратурной формулы (порядок ее точности) со степенью гладкости ядра интегрального уравнения. Если ядро и свободный член оказываются недостаточно гладкими, то для вычисления интеграла не следует применять высокоточные квадратуры, а лучше ограничится такими формулами, как формулы трапеций и прямоугольников.

Это замечание иллюстрирует рис.33, на котором представлено решение уравнения из примера 1, полученное при использовании квадратурной формулы Симпсона. Далее приведен листинг файла Solve2_g11.m (листинг 4), содержащего описание соответствующей функции.

Листинг 4. Файл Solve2_g11.m function [X,Y]=solve2_g11(x1,x2,N,Lambda) % задание временной сетки h=(x2-x1)/(N-1);

i=1:N; t(i)=x1+h*(i-1); s=t;

% задание коэффициентов квадратурной формулы метода Симпсона

A(1)=1/3;

A(N)=1/3;

k=0;

for i=2:N-1 if k==0 A(i)=4/3; k=1;

else A(i)=2/3; k=0;

end;

% вычисление значений функции Q(t,s) в узлах сетки for i=1:N

for j=1:N q(i,j)=Q11(t(i),s(j)); end;

267

268

end;

% вычисление значений функции f(t) в узлах временной сетки

F=f11(t); for i=1:N for j=1:N if i==j

M(i,j)=1-Lambda*A(i)*q(i,j)*h; else M(i,j)=-Lambda*A(i)*q(i,j)*h; end;

end;

X=t;

Y=M^-1*F'; % нахождение решения интегрального уравнения

Для получения численного решения интегрального уравнения следует создать файлы q11.m, f11.m, Solve1_g11 и затем выполнить следующую последовательность команд:

>>x1=1; % левая граница отрезка поиска решения

>>x2=2; % правая граница отрезка поиска решения

>>Lambda=1;

>>N=300; % число узлов разбиения отрезка

>>[X,Y]=solve2_g11(x1,x2,N,Lambda);

>>plot(X,Y) % визуализация решения интегрального уравнения

(рис. 33)

269

Рис. 33. Численное решение интегрального уравнения

2	x(s)ds
x(t) = ∫	t + s	2	+ t + 1 − t + 4 + t.
1	t + s

при использовании формулы Симпсона

2.3. Квадратурный метод решения интегральных уравнений Вольтерра

Так как линейные интегральные уравнения Вольтерра в отличие от уравнения Фредгольма имеют единственное непрерывное решение при любых значениях параметра λ, при нахождении численного решения уравнения

t
x(t) = ∫Q(t, s)x(s)ds + f (t),	(18)

где t [а, Ь], можно положить λ = 1.

Учитывая, что уравнение Вольтерра формально можно считать уравнением Фредгольма вида

t
x(t) = ∫Q(t, s)x(s)ds + f (t)	(19)

с ядром

270

Q(t, s) при a ≤ s ≤ t ≤ b
K(t, s) =	при a ≤ t ≤ s ≤ b	,
0

для нахождения решения рассматриваемого воспользуемся результатами предыдущего раздела.

Введем в рассмотрение временную сетку

(20)

уравнения

s j [a, b] ,

состоящую из п узлов, и выберем конкретную квадратурную формулу с весами Аj, тогда приближенное решение интегрального уравнения принимает вид (16). Составим систему линейных алгебраических уравнений, аналогичную системе (17), которая в силу свойств ядра интегрального уравнения (20) вырождается в треугольную:

(1 − A1Q11 )x1 = f1

− A1Q21 x1 + (1 − A2Q22 )x2 =

(21)

− A Q

−K+ (1

− A Q

= f

Из (21) видно, что искомые значения x1, x2,…,хп находятся последовательными вычислениями по следующим формулам:

x1	=			f1	,			(22)
x1	=		1	− A1Q11	,			(22)
			1	− A1Q11
				i−1
		fi + ∑Aj Qij x j
xi =				j=1		,		(23)
xi =				1 − Ai Qii		,		(23)
				1 − Ai Qii
Пример 2. Найти решение в пакете МАТLАВ
интегрального уравнения
x(t) = ∫t cos2 (ts3 )x(s)ds + t 2 −						1	tg(t 4 ).
x(t) = ∫t cos2 (ts3 )x(s)ds + t 2 −						3	tg(t 4 ).
3						3

(Точное решение уравнения х = t2.)

1. Создайте файл q11_2.m (листинг 5), содержащий описание функции, возвращающей значения подынтегральной функции.

271

Листинг 5. Файл q11_2.m function z=Q11_2(t,s) z=t*cos(t*s.^3).^2;

2.Создайте файл F11_2.m (листинг 6), содержащий описание функции, возвращающей значения функции f(t).

Листинг 6. Файл F11_2.m function z=f11_2(t) z=t.^2-1/3*tan(t.^4);

3.Создайте файл Solve3_g11.m (листинг 7), содержащий описание функции, возвращающей решение интегрального уравнения.

Листинг 7. Файл Solve3_g11.m function [T,Y]=Solve3_g11(t1,t2,N) % задание временной сетки h=(t2-t1)/(N-1);

i=1:N; t(i)=t1+h*(i-1); s=t;

% задание коэффициентов квадратурной формулы метода трапеций

A(1)=0.5; m=2:N-1; A(m)=1; A(N)=0.5;

%вычисление значений функции Q(t,s) в узлах сетки for i=1:N

for j=1:N Q(i,j)=Q11_2(t(i),s(j)); end;

end;

%вычисление значений функции f(t) в узлах временной сетки

F=f11_2(t);

%вычисление решения интегрального уравнения

x(1)=F(1)./(1-A(1)*Q(1,1)); for m=2:N

S=0;

272

for j=1:m-1 S=S+h.*A(j).*Q(m,j).*x(j); end;

x(m)=(F(m)+S)./(1-h.*A(m).*Q(m,m)); end;

T=t;

Y=x;

4. Выполните следующую последовательность команд:

>>t1=0; % левая граница отрезка поиска решения

>>t2=0.5; % правая граница отрезка поиска решения

>>N=300; % число узлов разбиения отрезка

>>[X,Y]=solve3_g11(x1,x2,N,Lambda);

>>plot(X,Y)%визуализация решения интегрального уравнения

% (рис. 34)

Рис. 34. Численное решение интегрального уравнения

x(t) = ∫t cos2 (ts3 )x(s)ds + t 2	−	1	tg(t 4 ).
		3
3

% оценка параметров решения интегрального уравнения %методом наименьших квадратов

>>Z=[ones(size(X'))X'X'.^2];

>>a=Z\Y'

-0.0000 -0.0000 1.0003

>>format long

>>a

1.0е+002*

-0.00000187595514 -0.00000470664690 1.00030838604155

Получим расчетные формулы для решения уравнения Вольтерра первого рода (5) при использовании метода средних прямоугольников. Решения уравнения будем находить в узлах временной сетки

t1 = a + h, t2 = t1 + h,K, ti = ti−1 + h.	(24)
Подставляя (24) в (4), получаем равенства
ti
∫Q(TI , s)x(s)ds = f (ti ).	(25)

274

273

Рис. 35. Пространственно-временная сетка, используемая для решения уравнения Вольтера

Из (25) видно, что в данном случае условие совпадения узлов квадратур si с узлами временной сетки ti не является обязательным, поэтому их можно выбрать посередине элементарных промежутков интегрирования [ti-1, ti] (рис. 35). Выбор данной сетки означает, что

x1 ≈ x(s1 ), x2 ≈ x(s2 ),K, xn ≈ x(sn ).								(26)
Учитывая выбор квадратурной формулы и условия (26),
запишем (25) в следующем виде:
hQ(t1 , s1 )x1 = f (t1 ),
hQ(t2 , s1 )x1 + hQ(t2 , s2 )x2 = f (t2 ),								(27)
hQ(t3 , s1 )x1 + hQ(t3 , s2 )x2			+ hQ(t3 , s3 )x3 = f (t3 ),
		K,				h
где		si	= ti	−			.

					2
Из равенств (27) последовательно находим:
x1	=	f	(t1 )		,			(28)
		hQ(t1 , s1 )

		275

	i−1
	f (ti ) − h∑Q(ti , s j )x j
xi =	i=1	,	(29)
xi =	hQ(ti , si )	,	(29)
	hQ(ti , si )

где i = 2, 3,

Пример 4. Найти в пакете МАТЬАВ решение интегрального уравнения

t	1
∫(t 2 + s 2 +1)x(s)ds = t 2 −	1		,
∫(t 2 + s 2 +1)x(s)ds = t 2 −		t	,
1		t

используя систему узлов координатно-временной сетеки, представленную на рис. 35.

(Точное решение уравнения x(t) = t12 . )

1. Создайте файл F11_4.m (листинг 8), содержащий описание функции, возвращающей значения функции f(t).

Листинг 8. Файл F11_4.m function z=F11_4(t) z=t.^2-1./t;

2. Создайте файл Q11_4.m (листинг 9), содержащий описание функции, возвращающей значения функции Q(t,s).

Листинг 9. Файл Q11_4.m function z=Q11_4(t,s) z=t.^2+s.^2+1;

3. Создайте файл Volterra11.m (листинг 10), содержащий описание функции, возвращающей решения интегрального уравнения Вольтерра.

Листинг 11.10. Файл Volterra11.m function [T,Z]=Volterra11(t1,t2,N)

%задание временной сетки h=(t2-t1)/(N-1);

i=1:N;

t(i)=t1+h*i;

s=t+h/2;

%вычисление значений ядра интегрального уравнения в узлах временной сетки

276

fоr i=1:N fоr j=1:N

q(i+1,j+1)=Q11_4(t(i),s(j)); end;

end;

%вычисление значений функции F(t) в узлах временной сетки

F(1)=F11_4(t(1)); F(i+1)=F11_4(t(1));

%Вычисление значений решения интегрального уравнения в соответствие с (28),(29)

х(1)=F(1)/(h*q(1,1)); for m=2:N

s=0;

fоr j=2:m-1 s=s+q(m,j)*m(j); еnd;

х(m) = (F(m) -h*s)/( h*q(m,m)); end;

Т=t; Z=х;

4. Выполните следующую последовательность команд:

>>t1=1; % левая граница интервала поиска решения

>>t2=1.3; % правая граница интервала поиска решения

>>N=300; % число интервалов разбиения отрезка

[t1,t2]

>>[Т,Z]=Voltегга11(t1,t2,N); % численного решения интегрального уравнения Вольтерра

>>рlоt(Т,Z); % визуализация решения уравнения Вольтерра (рис. 36)

277

Рис. 36. Численное решение интегрального уравнения

на пространственно-временной сетке, представленной на рис 35.

При использовании квадратурных формул замкнутого типа и совпадающей системы узлов возникает проблема вычисления значения x1=x(t1)=x(s1)=x(a), которая не возникала при решении уравнений Вольтерра второго рода. Действительно, при i=1 равенство (25) теряет всякий смысл.

Для нахождения начального значения x1 продифференцируем уравнение (5) по t.

t
Q(t, t)x(t) + ∫Q′(t, s)x(s)ds = f ′(t).			(30)
a
Положив в (30) t= а, получим		′	(31)
		′
Q(a, a)x(a) = f (a).
Откуда следует, что	f ′(a)
x(a) +	f ′(a)	,
x(a) +	Q(a, a)	,
	Q(a, a)
	278

следовательно,

x1 =	f ′(a)	.	(32)

	Q11

При использовании квадратурной формулы трапеций далее получаем:

Q21 x1

= f

Q22

Q31 x1

− hQ32 x2

= f

Q33

т. е. в общем случае при любом j= 2, 3,

j−1

f j −

Q j1 x1 − h∑Q jk xk

x(s j

) ≈ x j

k =2

(33)

Q jj

Пример 4. Найти в пакете МАТ1АВ решение

интегрального уравнения

∫(t 2 + s 2 +1)x(s)ds = t 2 −

используя замкнутые квадратурные формулы.

1. Создайте файл F11_4.m (листинг 11), содержащий описание функции, возвращающей значения функции f(t).

Листинг 11. Файл F11_4.m function z=F11_4(t) z=t.^2-1./t;

2. Создайте файл dF11_4.m (листинг 12), содержащий описание функции, возвращающей значения производной

функции f(t).	279

Листинг 12. Файл dF11_4.m function z=dF11_4(t) z=2*t+1/t.^2;

3. Создайте файл Q11_4.m (листинг 13), содержащий описание функции, возвращающей значения функции Q(t,s).

Листинг 13. Файл Q11_4.m function z=Q11_4(t) z=t.^2+s.^2+1;

4. Создайте	файл	Volterra11_2.m	(листинг 14),
содержащий	описание	функции, возвращающей решения

интегрального уравнения Вольтерра на совпадающей сетке.

Листинг 14. Файл Volterra11_2.m function [T,Z]=Volterra11(t1,t2,N)

%задание временной сетки h=(t2-t1)/(N-1);

i=1:N; t(i)=t1+h*(i-1); s=t;

%вычисление значений ядра интегрального уравнения в узлах временной сетки

fоr i=1:N fоr j=1:N

q(i,j)=Q11_4(t(i),s(j)); end;

end;

%вычисление значений решения интегрального уравнения в соответствие с (32), (33) F=F11_4(t);

F(1)=dF11_4(t(1)); х(1)=F(1)/(h*q(1,1)); for m=2:N

s=0;

fоr j=2:m-1 s=s+q(m,j)*m(j); еnd;

280

х(m) = (F(m) -h*s)/( h*q(m,m)); end;

Т=t; Z=х;

5. Выполните следующую последовательность команд:

>>t1=1; % левая граница интервала поиска решения

>>t2=1.3; % правая граница интервала поиска решения

>>N=300; % число интервалов разбиения отрезка

[t1,t2]

>>[Т 2]=Vо1tеrrа11_2 (t1,t2,N) ; % численного решения интегрального уравнения Вольтерра

>>рlо1; (Т,Z); % визуализация решения уравнения Вольтерра (рис. 37)

	Рис. 37. Численное решение интегрального уравнения
t		1	, полученное при использовании замкнутых
∫(t 2	+ s2 +1)x(s)ds = t 2 −
1		t
	квадратурных формул

281

Приложение Употребление графических сокращений

Правила	сокращений		слов	и	словосочетаний
устанавливаются ГОСТ 7.12-77, ГОСТ 7.12-93.
	Допускается сокращать:
авт. – автор			т.е. - то есть
автореф. – автореферат			и т.д. - и так далее
а.с. – авторское			и т.п. - и тому подобное (после
свидетельство		перечисления)
адм. -			и др. - и другие
административный			и пр. - и прочие
акад. — академия			см. — смотри (при повторной
АО - акционерное		ссылке)
общество			напр. - например
аннот. - аннотация			в., вв., гг. - при датах;
ж.д. -			г., д., обл., с. - при
железнодорожный		географических названиях;
ил. - иллюстрация			г-жа, г-н, им., т. - при фамилии и
им. - имени		названиях;
т. - том			гл., п., подп., разд., рис., с., см.,
тт. – тома		ср., табл., ч. - при ссылках;
ин-т - институт			млн, млрд, тыс., экз. - при числах
тип. - типография		в цифровой форме;
с. - страница			гр. - гражданин:
напр. – например			п/п - по порядку.
проф. - профессор			т.о. — таким образом;
акад. - академик			т.н. — так называемый;
доц. - доцент			т.к. - так как.
с – секунда			учен. - ученый
ч – час			канд. - кандидат
т - тонна			техн. - технический
			282

В специальной литературе допускается употребление без расшифровки только сокращений, понятных читателю: ЭВМ, ЭДС, КПД, ГЭС, НПО и т.п. Другие сокращения должны быть расшифрованы при первом упоминании текста или приводится в отдельном списке условных сокращений.

Форма сокращений по всей работе должна быть одинакова. Буквенные аббревиатуры - сокращения, образованные из первых букв слов, входящих в словосочетание, и произносимые при чтении в сокращенной форме: вуз, ЭВМ, НИИ, КЗоТ, ГАЗ-51, склоняются, если читаются по слогам, а не по буквам и род ведущего слова совпадает с родовой формой самой аббревиатуры. При этом падежное окончание пишется строчными буквами и слитно: МХАТа, вуза. ГОСТ,

ОСТ - сложносокращенные слова, не склоняются! Наращения при написании порядковых числительных:

1)5-й, 5-е, 5-м, 21-м или 17%-й раствор, если последней букве числительного предшествует гласная;

2)4-го, 4-му, 60-ми.

Знаки №, оС и т.д. при нескольких числах не удваивают и ставят один раз: № 5, 7, 9; от 50 до 60 оС; от 8 до 9 % и т.д.

Если в тексте приводят ряд (группу) числовых значений, выраженных одной и той же единицей физической величины, эту единицу указывают только после последней цифры ряда.

Пример: 5,9; 8,5; 10,0 см; 100 × 10 × 50 мм.

При стечении в конце сокращения двух одинаковых согласных одна усекается: ил., а не илл.

Даты

В современных документах принята следующая стандартная форма написания дат:

07.08.2001 г.; 2000/2001 учебный год;

90-е годы XX века; в 1960-1980 гг.; в период 1890-1910

годы. При датах в круглых скобках (1789-1793) - без

сокращения гг.	283

Правила компьютерного набора текста

Текст рукописи набирается на компьютере в редакторе Word. При наборе текста рекомендуется использовать основные системные гарнитуры шрифтов: Times New Roman Cyr, Arial Cyr и др. Размер основного шрифта - 12, межстрочный интервал - 1, формат бумаги А5. Для удобства печати рекомендуется использовать бумагу формата А4 с параметрами страницы: альбомная, поля 2 см по всем краям; выбрать Формат > Колонки > две (колонки одинаковой ширины 11,5 см).

Текст набирается с соблюдением следующих правил:

-абзацы отделяются друг от друга одним маркером конца абзаца (применение этого символа в других целях не допускается);

-все слова внутри абзаца разделяются только одним пробелом;

-перед знаком препинания пробелы не ставятся, после

знака препинания − один пробел;

-между последней цифрой числа и обозначением единицы измерения следует оставлять пробел (352 МПа, 30 оС, 10 %);

-при наборе должны различаться длинные тире (—)

(Alt+0151), короткие тире (−) (Alt+0150) и дефисы (-);

-между инициалами, после инициалов (перед фамилией), перед сокращениями и между ними ставится неразрывный пробел (Shift+Ctrl+Пробел), например, 1998 год, и т. д., т. е., и т. п., н. э., А.С.Пушкин и т. д.;

-выделения курсивом, полужирным, прописным обеспечиваются средствами Word.

Подчеркивания в качестве выделений не допускаются.

284

Формулы (ОСТ 29. 115-88)

Формулы набираются в редакторе формул, гарнитуры шрифтов: Times New Roman, Symbol. При наборе формул рекомендуется использовать следующие размеры шрифтов (для формата А5): основной - 12; крупный индекс - 8; мелкий индекс - 6; крупный символ -18; мелкий символ -12.

Латинские обозначения, кроме устойчивых форм, наименований типа:

max, min, cos, sin, tg, log, exp, det и т.д.

набираются курсивом.

Русские, греческие обозначения и цифры всегда набираются прямым шрифтом.

Построение формул. В состав редактора Word входит

Редактор формул (Equation Editor или MathType), который позволяет осуществлять набор формул полиграфического качества. Для вызова Редактора формул нажимается

одноименная кнопка . Меню Word заменится на меню Редактора формул, появится панель инструментов Формулы и один пустой слот для ввода формулы. Слот - это место, в которое помещается часть формулы. Количество слотов зависит от структуры формулы. Например, дробь имеет два слота: для числителя и знаменателя.

Панель инструментов Редактора формул содержит два ряда кнопок, каждая из которых открывает палитру. Верхние кнопки открывают палитры символов, а нижние кнопки открывают палитры шаблоном формул. Шаблон формулы - это готовая структура, состоящая из некоторых символов и слотов. Простые переменные вводятся с клавиатуры. С помощью

285

мышки или клавиши Tab можно перемещать точку вставки из слота в слот. Для закрытия Редактора формул надо щелкнуть кнопкой мышки в любом месте документа вне формулы. Чтобы вернуться к редактированию формулы, дважды щелкните по формуле.

Управление интервалами в формуле. Находясь в редакторе формул можно настроить параметры управления интервалами формулы. Для этого выполним команду ФорматИнтервал. Выделяя процентное значение того или иного параметра в окошке, правее показано, что означает данный параметр в формуле.

Выбор шрифтов. Шрифт вводимых символов задается автоматически в соответствии со стилем, который выбирается в меню Стиль Редактора формул. Обычно при работе в

Редакторе формул используется стиль Математический.

Выбор размеров шрифта. Редактор формул имеет не только несколько предопределенных стилей, но и несколько предопределенных размеров шрифтов. По умолчанию используется размер Обычный. Размер шрифта можно изменить, выбрав его в Редакторе формул из меню Размер.

Набор математических и химических формул должен быть по всему изданию единообразным по применению шрифтов и знаков, способу включения формул, набранных отдельными строчками, по применению индексов, линеек.

Математические символы в формулах набирают светлым курсивом, греческие и готические светлым прямым. Химические символы (Ag, Cu) - светлым прямым, сокращенные обозначения физических величин и единиц измерения (м, кВт, Ф/м, W/m) - светлым прямым без точек. Числа и дроби в формулах всегда должны быть набраны

286

прямым шрифтом. Перенос в формулах допускается делать на знаках соотношений (=,≈,<,>), на отточии (...), на знаках (+) и (-), (×) с дублированием знака на другой строке.

Например, f (x1 ,x2,...,xn) = = b0 +bу+...+bn,.

Нумеровать следует наиболее важные формулы, на которые приводятся ссылки в последующем тексте. В зависимости от объема издания и его структуры используется сквозная и индексационная нумерация формул, таблиц, рисунков. Индексационная нумерация используется, как правило, при делении текста на главы и параграфы.

В индексационном номере сначала арабскими цифрами указывают номер главы (раздела), затем (после точки) ставится порядковый номер формулы в данной главе. Номер формулы заключается в круглые скобки и выравнивается по

правому краю печатного листа.
Например,
1)---------		(3.1)
2)_________________________________.		(3.2)
3) __________________ ,
_______________ ,		(3.3)
_______________ .		(3.3)
_______________ .
4) ________________ ;		(3.4)
_____________ ;		(3.4)
_____________ .	287

…………………….

5) ________________ . (3.5)

..…………………..

Последовательность расшифровки буквенных обозначений (экспликация) должна соответствовать последовательности расположения этих обозначений в формуле. После формулы перед экспликацией ставят запятую, затем с новой строки без отступа от левого края набирается слово "где" (без двоеточия), за ним в этой же строке следует обозначение первой величины, после тире - ее расшифровка и далее, через запятую единица измерения. Все элементы располагаются в строку в целях экономии бумаги. В конце каждого элемента расшифровки ставят точку с запятой, а в конце последнего - точку.

Расшифровка дроби: сначала поясняют обозначения величин, помещенных в числителе, в том же порядке, что и в формуле, а затем - в знаменателе.

В формулах допускается использовать все виды скобок: (),{},[], и т.д. Высота скобок должна быть достаточной, чтобы охватывать находящееся в них выражение.

Основным знаком умножения является точка на средней линии. Она ставится:

а) между числовыми сомножителями: 20 75 ;

б) для выделения какого-либо множителя: 2 2ху z;

288

в) для записи скалярного произведения векторов: а b; г) между аргументом тригонометрической функции и

буквенным обозначением:

a cos x b sin y,

д) между знаком радикала и сомножителем: b a sin x.

Точка как знак умножения не ставится:

а) между числом и буквенным символом 5ab; б) перед скобками и после них (b+c)(a-d);

в) перед дробными выражениями и после них; г) перед знаком интеграла, радикала, логарифма:

д) перед аргументом тригонометрической функции: arccos ωt.

Косой крест в качестве знака умножения ставят:

а) при указании размеров: 4,5×3м;

б) при записи векторного произведения a × b; в) при переносе формулы на знаке умножения:

289

Расположение формул в тексте работы

Наиболее важные формулы, а также длинные и громоздкие формулы, содержащие знаки суммирования, произведения, дифференцирования, интегрирования, располагают на отдельных строках. Там же - и все нумерованные формулы. Для экономии места несколько коротких однотипных формул, выделенных из текста, можно помещать на одной строке, а не одну под другой. Небольшие и несложные формулы, не имеющие самостоятельного значения, размещают внутри строк текста.

На все нумерованные формулы обязательно должны быть ссылки. Они оформляются в той же графической форме, что и после формулы, т.е. арабскими цифрами в круглых скобках.

Например: в формуле (3.7); из уравнения (5.4) вытекает... и т.д. Следует знать и правила пунктуации в тексте с формулами. Формулы включаются в предложение как его равноправный элемент, поэтому в конце формулы и в тексте перед ними знаки препинания ставят в соответствии с

правилами пунктуации.

Двоеточие перед формулами ставят: а) после обобщающего слова;

б) если этого требует построение текста, предшествующего формуле.

290

Многоточие применяется при пропуске членов в ряду суммирования, вычитания или равенства. При этом знаки операции ставятся и перед многоточием и после него:

В системах уравнений, в матрицах и определителях при пропуске строк делается отточие на полную строку:

5 0 0 0

0 5 0 0

. . . .

0 0 0 5

Таблицы

Основные требования к содержанию и оформлению таблиц - существенность, полнота показателей, характеризирующих процесс, предмет или явление, четкость и ясность представления, экономичность, единообразие. Ссылка на таблицу в тексте обязательна и должна быть до представления (расположения) самой таблицы. Ссылка должна органически входить в текст, а не выделяться в самостоятельную фразу, повторяющую тематический заголовок таблицы (табл. 2).

Слово "таблица" и ее порядковый номер (арабскими цифрами) ставят над заголовком в правом верхнем углу, выделяя его курсивом или разрядкой. Название помещают на следующей строке по центру291. Например:

Таблица 2

	Корректурные знаки и их применение

	Начертание знаков	Назначение	Применение	***

1.	****	****	****	****

Обычно таблица состоит из следующих элементов:

-порядковый номер и тематический заголовок;

-боковик;

-заголовки вертикальных граф (головка);

-горизонтальные и вертикальные графы (основная

часть).

Боковик, как и головка, должен быть лаконичным, обычно в Им. п. ед. или мн. числа. После заголовков таблицы, боковика, граф точки не ставят.

Графа "номер по порядку" не допускается. Если в тексте только одна таблица, то номер ей не присваивается, слово "таблица" не пишется.

При переносе таблицы на следующую страницу головка не повторяется. В этом случае пронумеровывают графы и

повторяют их нумерацию на следующей странице, а вместо тематического заголовка пишут "Продолжение табл. 1.2". Если таблица продолжается на трех и более страницах, на последней странице пишут "Окончание табл. 1.2".

Иллюстративный материал

Иллюстрации (рисунки) должны обогащать содержание печатного произведения, помогать читателю лучше, полнее и глубже воспринимать его. Каждая имеющаяся иллюстрация должна отвечать тексту, а текст - иллюстрации. Все иллюстрации должны быть пронумерованы. Обычно используется сквозная или индексационная (подглавная) нумерация. Если рисунок один - он не нумеруется, ссылка на него делается словом "рисунок" без сокращений, а под самим рисунком ничего не пишется.

Рисунок необходимо помещать на той же полосе или на развороте, что и ссылка на него.

Ссылка на рисунок состоит:

1) из условного названия и порядкового номера с необходимым контекстом, оборотом речи: Например: "Как видно из рис.3..."; "... представлен на рисунке 5.1"; сокращение "см." используется при повторной ссылке на рисунок:

293

292

Например: (см. рис.4); можно делать ссылку в круглых скобках: (рис.5);

2) условного названия иллюстрации, порядкового номера и буквенного или словесного обозначения ее части. Например: (рис.1,а; рис.2, сверху и т.д.)

Каждая иллюстрация снабжается подрисуночной подписью. Подпись под иллюстрацией обычно имеет четыре основных элемента:

-наименование графического сюжета, обозначаемое сокращенно словом "Рис.";

-порядковый номер иллюстрации, который указывается без значка № арабскими цифрами;

-тематический заголовок иллюстрации (после точки с большой буквы);

-экспликацию (расшифровку рисунка), которая поясняет рисунок. Перед ней ставиться знак двоеточие. Между элементами экспликации точка с запятой.

Рис.38. Схема издательского комплекса

	а		б	в
Рис. 39............		: а -	......; б -	.......; в - ...........
Должно	быть	выдержано		единое	оформление

подрисуночных подписей. Подрисуночные подписи должны быть под самим рисунком либо рядом (зависит от способа расположения иллюстрации).

Рис……

Рис…

295

294

Способы размещения иллюстраций:

1)открытый (самый верх/низ полосы набора);

2)закрытый или вразрез полосы (внутри текста полосы);

3)"в оборку" (текст обрамляет иллюстрацию);

4) глухой (текст окружает рисунок со всех сторон);

5) полосной (рисунок занимает всю полосу). Внимание! Иллюстрация не должна завершать текст.

Общие правила выполнения чертежей регламентируются стандартами, входящими в Единую систему конструкторской документации (ЕСКД): ГОСТ 2.301-68 - ГОСТ 2.319-81.

Начертания и наименования линий регламентируются ГОСТ 2.303-68. Общие правила выполнения схем разного рода (электрических, кинематических, гидравлических, оптических, автоматизации и т.п.) регламентируются ГОСТ

2.701-76.

Правила выполнения диаграмм - ГОСТ 2.319-81.

Нормативные ссылки

Методические рекомендации составлены в соответствии с системой стандартов по информации, библиотечному и издательскому делу (СИБИД), которые определяют требования к оформлению изданий, содержат перечень необходимых и достаточных сведений и порядок их приведения в издательской продукции, а также регламентируют требования к информационнобиблиографическому аппарату самих изданий.

ГОСТ 7.1-84 “Библиографическое описание документа. Общие требования и правила составления”

ГОСТ 7.4-95 “Издания. Выходные сведения” ГОСТ 7.5-98 “Журналы, сборники, информационные издания. Издательское оформление публикуемых материалов”

ГОСТ 7.9-95 “Реферат и аннотация. Общие требования” ГОСТ 7.12-93 “Библиографическая запись. Сокращение

слов на русском языке. Общие требования и правила” ГОСТ 7.51-98 “Карточки для каталогов и картотек.

Каталогизация в издании. Состав, структура данных и издательское оформление”

ГОСТ 7.53-86 “Издание. Международная стандартная нумерация книг”

297

296

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.57 Mб12903.pdf
#
15.11.20222.57 Mб12904.pdf
#
15.11.20222.57 Mб02905.pdf
#
15.11.20222.58 Mб02906.pdf
#
15.11.20222.58 Mб72909.pdf
#
15.11.20222.58 Mб102910.pdf
#
15.11.20222.59 Mб02912.pdf
#
15.11.20222.59 Mб02914.pdf
#
15.11.20222.59 Mб12915.pdf
#
15.11.20222.6 Mб22916.pdf
#
15.11.20222.6 Mб02917.pdf