Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2910.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.58 Mб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

ϕ0 (x − at)−ϕ0

(x − at)

u (x, t)−u(x, t)

(x + at)−ϕ0 (x + at)

ϕ0

x+at

ϕ1(α)−ϕ1

(α)

dα ,

2a ∫x−at

или, используя соотношения (3) ,

u (x,t)−u(x,t)

atδ ≤ δ(1

+ t0 ).

Если положить δ =

то из последнего неравенства

получаем

1 + t0

(x,t)−u

(x,t)

< ε

для всех 0 ≤ t ≤ t0 ,

− ∞ < x < +∞.

Таким образом, для волнового уравнения

∂2u

= a

2 ∂2u

∂t2

∂x2

задача Коши поставлена корректно.

Приведем пример Адамара некорректно поставленной задачи. Рассмотрим задачу Коши: найти решение уравнения Лапласа

∂2u	= a	2 ∂2u		, t > 0 , − ∞ < x < +∞						(4)
∂t2	= a	∂x2		, t > 0 , − ∞ < x < +∞						(4)
∂t2		∂x2
удовлетворяющее при t = 0 условиям
			u \|t =0 = 0 ,							(5)
		∂u				=		1	sin nx	(6)
		∂u						1

		∂t		t =0				n
		∂t		t =0				n
( n — натуральное число).
Легко проверить, что решением этой задачи будет
функция				1
	u(x,t)=			1			sh nt sin nx .			(7)
	u(x,t)=				n2		sh nt sin nx .			(7)
					n2
				33

Так как
	∂u(x,0)	=	1	sin nx	≤	1	,

	∂t					n
			n
то при достаточно большом		n	абсолютная величина ut (x,t)

как угодно мала при любом х. Вместе с тем, как показывает формула (7), решение u(x,t) рассматриваемой задачи будет

принимать как угодно большие по абсолютной величине значения при произвольно малом t > 0 , если n достаточно велико.

Допустим, что мы нашли решение u0 (x,t) задачи Коши для уравнения (4) при некоторых начальных условиях

u |

=ϕ

(x), ∂u

=ϕ

(x),

t =0

∂t

Тогда для начальных условий

t =0

u |

=ϕ

(x),

∂u

=ϕ (x)+

sin nx ,

t =0

∂t

t =0

решением задачи Коши будет функция

u(x,t)= u

(x,t)+

sh nt sin nx .

Отсюда видно, что малое изменение начальных условий может повлечь за собой как угодно большие изменения решения задачи Коши и притом в любой близости от линии начальных значений t = 0 .

Следовательно, задача Коши для уравнения Лапласа

является некорректно поставленной.
Рассмотрим теперь гиперболическое уравнение
uxy = 0	(8)

и поставим следующую задачу: найти решение u(x, y) уравнения (8) в прямоугольнике Q со сторонами,

параллельными координатным осям (рис. 6), принимающее на границе Г этого прямоугольника заданные граничные значения.

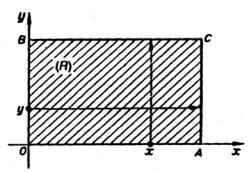
Эта (граничная) задача, вообще говоря, не имеет решения. В самом деле, обратимся к общему решению уравнения (8)

u(x, y)= f (x)+ g(y)

Рис.6

(здесь f и g — произвольные дифференцируемые функции). Так как производная uy = g′(y) должна принимать одинаковые

значения в соответствующих противолежащих точках сторон x = const прямоугольника Q, а производная ux = f ′(x) — в

соответствующих противолежащих точках сторон у = const, то мы не можем произвольно задавать граничные значения.

Значения функции u(x, y) можно задавать произвольно

только на двух смежных сторонах прямоугольника (например, на OA и на OB ), а не на всей его границе Г, так что для гиперболического уравнения поставленная граничная задача оказывается переопределенной.

Замечание 1. Подчеркнем, что волновое уравнение и уравнение Лапласа являются уравнениями разных типов: волновое уравнение имеет гиперболический тип, а уравнение Лапласа — эллиптический.

Замечание 2. Некорректно поставленные задачи часто встречаются в приложениях. К их числу относятся многие хорошо известные математические задачи, в частности, приведенная выше задача Коши для уравнения Лапласа связана с обратной задачей гравиметрии об определении

формы тела по создаваемой им аномалии силы тяжести. Метод Фурье, или метод разделения переменных, является

одним из наиболее распространенных методов решения уравнений с частными производными. Рассмотрим этот метод, обратившись к простейшей задаче о свободных колебаниях однородной струны длины l , закрепленной на концах.

4. Свободные колебания однородной струны, закрепленной на концах

Задача о свободных колебаниях однородной струны с закрепленными концами сводится к решению уравнения

∂2u	= a		2	∂2u		, t > 0 , 0		< x < l ,	(1)
∂t2	= a			∂x2		, t > 0 , 0		< x < l ,	(1)
∂t2				∂x2
при граничных условиях								t ≥ 0
и начальных условиях		u \|x=0 = u \|x=l = 0 ,						t ≥ 0	(2)
и начальных условиях
u \|		=ϕ		0	(x), ∂u		=ϕ (x), 0 < x < l ,		(3)
u \|		=ϕ			(x), ∂u		=ϕ (x), 0 < x < l ,		(3)
t =0						∂t	t =0	1
						∂t	t =0

Задачу (1)-(3) называют смешанной: она содержит и начальные и граничные условия.

Решение задачи начнем с поиска частных решений

уравнения (1) вида
u(x,t)= T (t)X (x).	(4)

При этом будем предполагать, что каждое из них удовлетворяет граничным условиям (2), но не равно нулю тождественно. Подставляя функцию u(x,t) в форме (4) в

уравнение (1) , получаем

T′′(t)X (x)= a2T (t)X ′′(x),

или

′′		′′
T (t)		X (x)
	=		.
a2T (t)		X (x)

Последнее равенство (его левая часть зависит только от t, 36

а правая — только от х) возможно лишь в том случае, если обе его части не зависят ни от t, ни от х, т. е. равны одной и той же

постоянной. Обозначим эту постоянную (разделения) через

(− λ),

(t)

X (x)

′′

= −λ .

(5)

a2T (t)

X (x)

Из

равенства

(5)

получаем

два

обыкновенных

дифференциальных уравнения

′′

(6)

(t)+ λa T (t)= 0 ,

′′

λX (x)= 0 .

(7)

X (x)+

Граничные условия (2) дают

u(0,t)= X

(0)T (t)= 0 , u(l,t)= X (l)T (t)= 0 ,

откуда (T (t)≡ 0)

следует,

что

функция

Х(х) должна

удовлетворять граничным условиям

(0)= 0 , X (l)= 0 .

(8)

Чтобы получить нетривиальные решения u(x,t) вида (4) ,

удовлетворяющие граничным условиям (2), необходимо найти нетривиальные решения уравнения

′′	,	(7)
X (x)+ λX (x)= 0
удовлетворяющие граничным условиям
X (0)= 0 , X (l)= 0 .		(8)

Таким образом, мы приходим к следующей задаче: найти значения параметра λ , при которых существуют нетривиальные решения задачи (7)-(8), а также сами эти решения. Такие значения параметра λ называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями задачи

(7)-(8). Сформулированную таким образом задачу называют задачей Штурма— Лиувилля.

Найдем собственные значения и собственные функции задачи (7)-(8). Рассмотрим отдельно три случая, когда λ < 0 ,

λ = 0 , λ > 0 .

1. При λ < 0 общее решение уравнения (7) имеет вид

X (x)= C1e− −λ x + C2e −λ x .

Потребовав выполнения граничных условий (8), получим

C	+ C		2	= 0,
1								(9)
		− −λ x					−λ x
					+ C2e			= 0.
C1e
Так как определитель системы (9) отличен от нуля, то
C1 = 0 и C2 = 0 . Следовательно,						X (x)		= 0 , т. е. при λ < 0

нетривиальных решений задачи не существует.

2. При λ = 0 общее решение уравнения (7) имеет вид

X (x)= C1x + C2 ,

Граничные условия (8) дают

C1 0 + C2 = 0,C1l + C2 = 0,

откуда C1 = C2 = 0 и, следовательно, X (x)= 0 , т.е. при λ = 0

нетривиальных решений задачи (7)-(8) также не существует. 3. При λ > 0 общее решение уравнения (7) имеет вид

X (x )= C1 cos λ x + C 2 sin λ x .

Потребовав выполнение граничных условий (8), получим

C1 1 + C2 0 = 0,

C1 cos λx + C2 sin λx = 0. (10)

Система (10) имеет нетривиальные решения тогда и только тогда, когда определитель системы равен нулю,

1	0	λl	= 0 ,
cos λl	sin	λl

или sin λl = 0 , откуда λl = πk , где k — любое целое число. Таким образом, нетривиальные решения задачи (7)-(8) возможны лишь при

λk = sin klπ 2 , k =1,2,....

Это — собственные значения задачи (7)-(8).

Из первого уравнения системы (10) получаем, что C1 = 0 и, значит, функции

λk = sin klπ x , k =1,2,...

будут собственными функциями задачи. Собственные функции определены с точностью до постоянного множителя, который мы выбрали равным единице. При λ = λk общее

решение уравнения (6) имеет вид

Tk (t)= Ak cos kπl a t + Bk sin kπl a t ,

где Ak и Bk — произвольные постоянные. Таким образом, функции

uk (x,t)= Xk (x)Tk (t)= Ak cos kπl a t + Bk sin kπl a t sin klπ x

удовлетворяют уравнению (1) и граничным условиям (2)

при любых Ak и Bk , k =1,2,...,n,... .

В силу линейности и однородности уравнения (1) всякая конечная сумма решений будет также решением уравнения (1). То же справедливо и для ряда

∞	kπa		kπa		kπ
u(x,t)= ∑ Ak cos		t + Bk sin		t sin		x , (11)
u(x,t)= ∑ Ak cos	l	t + Bk sin	l	t sin	l	x , (11)
n=1	l		l		l

если он сходится равномерно и его можно дважды почленно дифференцировать по х и по t. Поскольку каждое слагаемое в ряде (11) удовлетворяет граничным условиям (2), то этим условиям будет удовлетворять и сумма u(x,t) этого ряда.

Остается определить в формуле (11) постоянные Ak и Bk так,

чтобы выполнялись и начальные условия (3). Продифференцируем формально ряд (11) по t. Имеем

∂u

∞

kπa

kπ

= ∑

−

Ak cos

+ Bk sin

sin

x .

(12)

∂t

n=1

Полагая в соотношениях (11) и

(12)

t = 0 , в

силу

начальных условий (3) получим

∞

kπ

∞

kπa

kπ

ϕ0 (x)= ∑Ak

sin

x ,

ϕ1(x)= ∑

Bk sin

x .

(13)

n=1

Формулы (13) представляют собой разложения заданных

функций ϕ0 (x)

и ϕ1(x)

в ряд Фурье по синусам в интервале

(0,l).

Коэффициенты разложений (13) вычисляются по

известным формулам

= 2

lϕ

(x)sin

kπ

xdx , B

l ϕ (x)sin

kπ

xdx

(14)

∫0

kπa ∫0

(k =1,2...),

Теорема 2. Если ϕ0 (x) C3[0,l] и удовлетворяет условиям

ϕ0 (0)

′′

=ϕ0 (l)= 0 , ϕ0 (0)=ϕ0

(l)= 0 ,

ϕ (x) C2 [0,l] и удовлетворяет условию

ϕ1(0)=ϕ1(l)= 0

u(x,t)

то

сумма

ряда (11),

где

определяются

формулами (14), имеет в области {0 < x < l,t > 0} непрерывные

частные производные до второго порядка включительно по каждому из аргументов, удовлетворяет уравнению (1), граничным условиям (2) и начальным условиям (3), т.е. является решением задачи (1)—(3).

Пример. Найти закон свободных колебаний однородной струны длины l , закрепленной на концах, если в начальный момент t = 0 струна имеет форму параболы hx(l − x)

(h > 0 − const), а начальная скорость отсутствует. Задача сводится к решению уравнения

∂2u		= a	2 ∂2u	, t	> 0		, 0 < x < l ,	(1)
∂t2		= a	∂x2	, t	> 0		, 0 < x < l ,	(1)
∂t2			∂x2
при граничных условиях
	u \|x=0 = 0 , u \|x=l = 0 , t ≥ 0 ,							(2)
и начальных условиях
u \|	= hx(l − x), ∂u						= 0 , 0 ≤ x ≤ l ,	(3)
u \|	= hx(l − x), ∂u						= 0 , 0 ≤ x ≤ l ,	(3)
t =0				∂t
						t =0
						t =0
Применяя метод Фурье, ищем							нетривиальные	решения

уравнения (1), удовлетворяющие граничным условиям (2) , в виде

u(x,t)= T (t)X (x).

(4)

Подставляя u(x,t) в форме (4) в уравнение (1) и разделяя

переменные, получим

(t)

(x)

′′

= −λ ,

(5)

a2T (t)

X (x)

откуда

′′

(6)

(t)+ λa T (t)= 0 ,

′′

(7)

(x)+ λX (x)= 0 ,

причем в силу (2)

X (l)= 0 .

X (0)= 0 ,

(8)

Как было установлено выше, собственные значения

задачи (7)-(8)

λn

nπ 2

, n =1,2,...

а соответствующие собственные функции

Xn (x)= sin

nπ

x n =1,2,...

Для λ = λn общее решение уравнения (6) имеет вид

T (t)= A

cos nπa t + B sin nπa t .

Будем искать решение исходной задачи в виде ряда

u(x,t)= ∑∞ An cos nπl a t + Bn sin nπl a t sin nπl a x . (9)

n=1

Для определения коэффициентов An и Bn воспользуемся начальными условиями (3). Имеем

u |t =0 = hx(l − x)

∞

nπ

= ∑An sin

x , 0 ≤ x ≤ l ,

(10)

n=1

= 0 = aπ

∞

∂u

∑nBn sin nπ x .

(11)

∂t

t =0

n=1

Из формулы (11) сразу получаем, что Bn = 0

для любого n , а

из (10)

nπ

l x(l − x)sin

xdx ,

l ∫0

откуда, интегрируя по частям дважды, находим

A2m+1 =

8l2h

, A2m+2

= 0 , m =1,2,...

π3 (2m +1)3

Подставляя

найденные

значения

ряд (9),

получим решение поставленной задачи

∞

(2m +1)πa

(2m +1)π

u(x,t)=

∑

cos

t sin

(2m +

m=0

ϕ0 (x)

ϕ1(x) не

Замечание.

Если

начальные функции

удовлетворяют условиям теоремы 2, то дважды непрерывно

дифференцируемого решения смешанной задачи (1)-(3) может
и		не		существовать.	Однако	если	ϕ0 (x) C1[0,l]	и
ϕ	0	(0)=ϕ	0	(l)= 0 , a ϕ (x) C0 [0,l] и ϕ (0)=ϕ (l)= 0 , то ряд (11)
	0		0	1		1	1
сходится равномерно при					0 ≤ x ≤ l	и любом t и определяет

непрерывную функцию u(x,t). В этом случае можно говорить

лишь об обобщенном решении задачи. Каждая из функций

u(x,t)= T (t)X (x).

uk (x,t)= Tk (t)Xk (x)= Ak cos kπl a t + Bk sin kπl a t sin klπ x

определяет так называемые собственные колебания струны, закрепленной на концах. При собственных колебаниях, отвечающих k =1, струна издает основной, самый низкий тон. При колебаниях, соответствующих большим k, она издает более высокие тоны, обертоны. Записав uk (x,t) в виде

uk (x,t)= Hk sin klπ xsin kπl a t +αk ,

заключаем, что собственные колебания струны — стоячие волны, при которых точки струны совершают гармонические

колебания с амплитудой Hk sin	kπ	x , частотой	ωk =	kπa	и
				l
	l

фазой αk .

Мы рассмотрели случай свободных колебаний однородной струны, закрепленной на концах. Рассмотрим


теперь случай других граничных условий. Пусть, например,
левый	конец	струны		закреплен, u(0,t)= 0 ,			а правый конец
x = l	упруго	связан		со своим положением			равновесия,	что
соответствует			условию		ux (l,t)= −hu(l,t)		(h > 0 − const).
Нетривиальное			решение		u(x,t)	уравнения		(1),

удовлетворяющее поставленным граничным условиям, будем опять искать в виде

В результате подстановки u(x,t)= T (t)X (x) в уравнение

(1) приходим к следующей задаче о собственных значениях: найти такие значения параметра λ , для которых дифференциальное уравнение

′′		(15)
X (x)+ λX (x)= 0		(15)
при граничных условиях
X (0)= 0 ,	′	(16)
X (0)= 0 ,	X (l)+ hX (l)= 0	(16)
	43

имеет нетривиальные решения X (x).

Общее решение уравнения (15) имеет вид (λ > 0)

X (x)= C1 cos λx + C2 sin λx .

Первое из граничных условий (16) дает C1 = 0 , так что функциями Х(х) с точностью до постоянного множителя

являются sin λx .
Из второго граничного условия (16) имеем
λ cos λl + hsin λl = 0 .			(17)
Положим λ = v2 . Тогда
tg(vl)= −	v	.	(18)

	h

Рис. 7

Для отыскания v получаем трансцендентное уравнение.

Корни этого уравнения можно найти графически, взяв в
плоскости	(v, z)	сечения последовательных ветвей кривой
z = tg(vl) прямой линией z = −			1 v (рис. 7).
			h
Обе	части	уравнения	(18) — нечетные функции
			44

относительно v, поэтому каждому положительному корню vk

соответствует равный ему по абсолютной величине отрицательный корень. Поскольку изменение знака vk не

влечет за собой появления новых собственных функций (они только изменят знак, что несущественно), достаточно ограничиться положительными корнями уравнения (18). В результате опять получается последовательность собственных значений λ1,λ2 ,...,λn ,... , и отвечающие им последовательности

собственных	функций	sin v1 x, sin v2 x,..., sin vn x,...						и
собственных колебаний
(A1 cos av1t + B1 sin av1t)sin v1x,...(An cos avnt + Bn sin avnt)sin vn x,...
Кстати, для n -ой собственной					частоты	vn	получается
асимптотическое соотношение
		lim	vn	=	π ,
		lim		=	π ,
		n→∞ n			l
в частности, для l = π имеем lim vn					=1.
		n→∞ n					ux (l,t)= 0 , то
Если правый конец струны x = l свободен,							ux (l,t)= 0 , то
из (17) получаем	cos vl = 0 .	Отсюда vl = π				+ nπ , так что в
					2

случае свободного конца собственные значения и собственные функции соответственно равны

vn = (2n2+l1)π , Xn (x)= sin (2n2+l1)π x (n = 0,1,2,...).

5. Вынужденные колебания струны, закрепленной на концах

Рассмотрим колебания однородной струны длины l, закрепленной на концах, под действием внешней силы f (x,t), рассчитанной на единицу длины. Эта задача приводит к

решению уравнения

∂2u = a

2 ∂2u + f (x,t)

(1)

∂t2

∂x2

при граничных условиях

и начальных условиях

u |x=0 = 0 , u |x=l = 0

(2)

u |

=ϕ

(x),

∂u

=ϕ (x),

(3)

∂t

t =0

Будем искать решение u(x,t) этой задачи в виде суммы

u(x,t)= v(x,t)+ w(x,t),

(4)

где v(x, t) — решение неоднородного уравнения

∂2v

= a2 ∂2v

+ f (x,t),

(5)

∂t2

∂x2

удовлетворяющим условиям

и начальным условиям

v |x=0 = 0 , v |x=l = 0

(6)

v |

=ϕ

(x),

∂v

=ϕ

(x),

(7)

∂t

t =0

а w(x,t) — решение однородного уравнения

∂2w

= a

2 ∂2w

(8)

∂t2

∂x2

удовлетворяет граничным условиям

и начальным условиям

w |x=0 = 0 ,

w |x=l = 0

(9)

w |

=ϕ

(x),

∂w

=ϕ (x),

(10)

t =0

∂t

Решение v(x,t)

t =0

представляет вынужденные

колебания

струны, т. е. такие колебания, которые совершаются под действием внешней возмущающей силы f (x,t), когда

начальные возмущения отсутствуют, а решение w(x,t)

представляет свободные колебания струны, т.е. такие колебания, которые происходят только вследствие начальных возмущений.

Метод нахождения свободных колебаний w(x,t) был изложен ранее, так что остается только найти вынужденные колебания v(x,t), т. е. решение неоднородного уравнения

(5)-(7).

Применим метод разложения по собственным функциям, который является одним из мощных методов решения неоднородных линейных уравнений с частными производными. Основная идея метода состоит в разложении внешней силы f (x,t) вряд

∞

f (x,t)= ∑ fk (t)Xk (x)

n=1

по собственным функциям {Xn (x)} соответствующей однородной краевой задачи и нахождении откликов uk (x,t) системы на воздействие каждой компоненты fk (t)Xk (x).

Суммируя все такие отклики, получим решение исходной задачи

∞

u(x,t)= ∑uk (x,t)

n=1

Решение v(x,t) задачи (5)-(7) будем искать в следующем виде:

∞
v(x,t)= ∑Tk (t)sin kπ x .		(11)
n=1	l

Здесь sin klπ x — собственные функции однородной краевой

задачи, и граничные условия (6) выполняются автоматически. Определим функции Tk (t) (k =1,2,...) так, чтобы функция

v(x,t) удовлетворяла уравнению (5) и начальным условиям (7).

Подставив v(x,t) в виде (11) в уравнение (5), получим

∞

k 2π2a2

kπ

′′

Tk (t) sin

x = f (x,t).

(12)

∑ Tk (t)+

n=1

Разложим функцию

f (x,t)

в интервале (0,l) в ряд Фурье по

синусам (собственным функциям)

kπ

∞

f (x,t)

= ∑ fk (t)sin

x ,

(13)

где

n=1

kπ

fk (t)=

l f (ξ,t)sin

ξdξ .

(14)

∫0

Сравнивая разложения (12) и (13) для одной и той же функции
f (x, t), получим дифференциальные уравнения
	k2π 2a2
′′			Tk (t)= fk (t) (k =1,2,...)	(15)

Tk (t)+ l2
для неизвестных функций Tk (t).
Чтобы решение		v(x,t), определяемое рядом		(11),

удовлетворяло нулевым начальным условиям (7), достаточно
подчинить функции Tk (t) условиям
Tk (0)= 0 , Tk′(0)= 0 (k =1,2,...).				(16)
Действительно, полагая в (11) t = 0 , получим
∞		kπ
v(x,0)= 0 = ∑Tk	(0)sin		x Tk (0)= 0 k .

n=1		l
Дифференцируя (11) по t	и полагая t = 0 , найдем,			что
Tk (0)= 0 k .

Пользуясь методом вариации постоянных, получим, что решения уравнений (15) при начальных условиях (16) имеют

вид	l				(τ )sin kπa (t −τ )dτ , (k =1,2,...), (17)
T (t)=	l	l	f	k
T (t)=		l	f
k	kπa ∫0				l
	kπa ∫0				l
					48

где fk (t) определяются по формулам (14).

Подставив найденные выражения для Tk (t) в ряд (11), получим решение v(x,t) задачи (5)-(7), если ряд (11) и ряды,

полученные из него почленным дифференцированием по х и по t дважды, сходятся равномерно.

Как можно показать, такая сходимость рядов будет обеспечена, если функция f (x,t) непрерывна, имеет

непрерывные частные производные по х до второго порядка включительно и для всех значений t выполняется условие f (0,t)= f (l,t)= 0 .

Тогда решение u(x,t) исходной задачи (1)-(3)

представляется в виде

kπa

kπ

∞

kπa

∞

u(x,t)= ∑ Ak cos

t +

Bk sin

t sin

x + ∑Tk

(t)sin

x ,

k =1

где функции Tk (t) определяются по формулам (17), а

A =

l ϕ

(x)sin

kπ

xdx ,

B =

lϕ (x)sin

kπ

xdx , (k =1,2,...)

∫0

kπa

∫0

Пример. Решить смешанную задачу

∂2u

+t sin x , t

> 0 , 0 < x <π ,

(1)

∂t2

∂x

u |x=0 = 0 , u

x=π = 0 , t ≥ 0 ,

(2)

u |

= 0 , ∂u

= 0 ,

0 ≤ x ≤ π ,

(3)

∂t

t =0

Начальные возмущения отсутствуют, так что мы имеем «чистую» задачу на вынужденные колебания однородной струны длины π , закрепленной на концах.

Система функций {sin nx} есть ортогональная на [0,π]

система	собственных	функций	краевой	задачи
′′	λX (x)= 0 , X (0)= X (π )= 0 (здесь λ = π ).
X (x)+	λX (x)= 0 , X (0)= X (π )= 0 (здесь λ = π ).

Ищем решение задачи (1)-(3) в виде

∞
u(x,t)= ∑Tn (t)sin nx ,	(4)

n=1

где Tn (t) — неизвестные функции. Подставляя u(x,t) в форме

(4) в уравнение (1), получим

∞	′′	2				= t sin x .

∑(Tn (t)+ n Tn (t))sin nx
n=1
откуда легко усматриваем, что				(t)= t ,
	′′						(5)
′′	T1	(t)+T1
	2		(t)= 0,		n = 2,3,...		(6)
Tn (t)+ n Tn

Используя формулу (4), в силу начальных условий (3) получаем

	∞			∞
	∞			∞
u(x,t)= 0 = ∑Tn (0)sin nx , ∂u				= 0 = ∑Tn′(0)sin nx ,
откуда	n=1	∂t	t =0	n=1
	n=1	∂t	t =0	n=1
	Tn (0)= Tn′(0)= 0 , (n =1,2,...).				(7)
	Tn (0)= Tn′(0)= 0 , (n =1,2,...).				(7)
Таким образом, для T1(t) имеем
		′′			(8)
		T1 (t)+T1(t)= t ,			(8)
		′			(9)
		T1(0)= T1(0)= 0 .			(9)
Выпишем общее решение уравнения (8)
	T1(t)	= C1 cost + C2 sin t + t .
Потребовав выполнение		начальных		условий (9),	находим
C1 = 0 , C2 = −1, так что
Для n ≥ 2 имеем	T1(t)= t −sin t .
Для n ≥ 2 имеем
′′				′
Tn (t)+ n Tn		(t)= 0, Tn (0)=Tn (0)= 0
	2

откуда Tn (t)≡ 0 (n = 2,3,...).

Пользуясь формулой (4), для решения u(x,t) исходной задачи получаем следующее выражение:

u(x,t)= (t −sin t)sin x . 50

6. Вынужденные колебания струны с подвижными концами

Рассмотрим вынужденные колебания однородной струны длины l под действием внешней силы f (x,t), рассчитанной на единицу длины, причем концы струны не закреплены, а

двигаются по заданному закону.
Эта задача приводится к решению уравнения
∂2u		= a2 ∂2u + f (x,t), t > 0 , 0 < x < l					(1)
∂t2				∂x2
при граничных условиях
u \|x=0 =ψ1					(t),	u \|x=l =ψ2 (t), t ≥ 0	(2)
и начальных условиях
u \|	=ϕ		0	(x),	∂u	=ϕ (x), 0 ≤ x ≤ l .	(3)

t =0					∂t	1
						t =0

К решению этой задачи метод Фурье непосредственно неприменим, т. к. граничные условия (2) неоднородны. Однако эта задача легко сводится к задаче с нулевыми (однородными) граничными условиями.

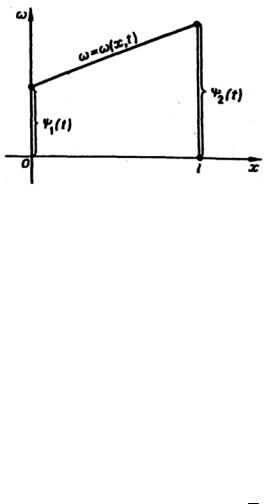
Действительно, введем вспомогательную функцию

ω(x,t)=ψ1(t)+[ψ2 (t)−ψ1(t)]	x	(4)
	l

Легко видеть, что
ω \|x=0 =ψ1(t), ω \|x=l =ψ2 (t),		(5)
Таким образом, функция ω(x,t) на концах		отрезка

0 ≤ x ≤ l удовлетворяет условиям (2), а	внутри этого отрезка
она линейна по x (рис. 8). Говорят,	что функция	ω(x,t)
продолжает граничные условия в интервале 0 < x < l .
Решение задачи (1)-(3) ищем в виде суммы
u(x,t)= v(x,t)+ω(x,t),		(6)

где v(x,t) — новая неизвестная функция. 51

Рис. 8

силу

выбора функции

x(v,t) функция

v = u −ω

удовлетворяет нулевым граничным условиям

v |x=0 = (u −ω)

|x=0 = 0 ,

v |x=l = (u −ω)|x=l = 0

(7)

и начальным условиям

v |t =0 = u |t =0 −ω |t =0 =ϕ0 (x)−ψ1

(0)−[ψ2

(0)

−ψ1(0)]

(x),

=ϕ0

(8)

∂u

∂ω

−[ψ2′(0)−ψ1′(0)]

−

=ϕ1(x)−ψ1′(0)

(x).

ϕ1

∂t

t =0

Подставив u = v +ω в уравнение (1), получим

∂2v

= a2 ∂2v

+ a2 ∂2ω −

∂2ω

+ f (x,t),

∂t2

∂x2

∂t2

где

f1(x,t)= f (x,t)−ψ1′′(t)−[ψ2′′(t)−ψ1′′(t)]xl .

Таким образом, при ψ1(t),ψ2 (t) C2 приходим к смешанной задаче с нулевыми граничными условиями для функции v(x,t): найти решение уравнения

∂2v = a2 ∂2v + f1(x,t),

∂t2 ∂x2

удовлетворяющее граничным условиям v |x=0 = v |x=l = 0 ,

и начальным условиям

∂v

v |t =0 =ϕ0 (x),

∂t

=ϕ1(x).

t =0

Метод решения таких задач был изложен ранее.

Пример. Решить смешанную задачу

∂2u

= a

∂2u

t > 0 ,

0 < x <1 ,

(1)

∂t2

∂x2

u |x=0 = t , u |x=1 = 2t ,

t ≥ 0 ,

(2)

u |

= 0 ,

∂u

=1+ x ,

0 ≤ x ≤1 ,

(3)

t =0

∂t

t =0

Граничные условия неоднородные (концы струны

подвижные).

Здесь

ψ1(t)

= t ,

ψ2 (t)= 2t .

Вводим

вспомогательную функцию

ω(x,t)= t + tx = t(1 + x).

(4)

Решение исходной задачи будем искать в виде

u(x,t)

= v(x,t)+ω(x,t),

(5)

где v(x,t) — новая неизвестная функция.

Для нее получаем уравнение

∂2v

= a

∂2v

t > 0 ,

0 < x <1 ,

(6)

∂t2

∂x2

граничные условия

v |x=0 = v |x=1 = 0 ,

начальные условия

(7)

v |

= 0 ,

∂v

= 0 .

(8)

t =0

∂t

t =0

Задача (6)-(8) имеет очевидное решение v(x,t)= 0 , и, как

ясно из физических

соображений,

это ее единственное

решение. Тогда по формуле (5) получаем решение u(x,t)

исходной задачи

u(x,t)= t(1 + x).

7. Общая схема метода Фурье
Рассмотрим	в			области			Q = {t > 0,0 < x < l}
дифференциальное уравнение
		∂2u			∂		∂u
ρ(x)=		∂t2	=			p(x)	− q(x)u	(1)

					∂x		∂x
(уравнение колебаний		неоднородной					струны длины l ), где
ρ(x)> 0 , p(x)> 0 ,	q(x)≥ 0 для 0 ≤ x ≤ l , так что уравнение (1)

является уравнением гиперболического типа в области Q. Предположим, что

ρ(x) C[0,l], p(x) C1[0,l], q(x) C[0,l],

изаймемся изучением смешанной задачи для уравнения (1)

при однородных граничных условиях

αu(0,t)+ βux (0,t)= 0 , γu(l,t)+δux (l,t)= 0 , t ≥ 0 .

где α, β,γ,δ — некоторые постоянные, причем α2 + β2 ≠ 0 , γ 2 +δ 2 ≠ 0 . (Напомним, что задача называется однородной,

если, наряду с решением u этой задачи, ее решением является также cu , где c — произвольная постоянная.)

Возможны граничные условия следующих типов:

1.u(0,t)= 0 и u(l,t)= 0 (струна с закрепленными концами

(рис. 9 а));

2.ux (0,t)= 0 и ux (l,t)= 0 (струна со свободными концами

(рис. 9 б));

3. ux (0,t)= h0u(0,t) и ux (l,t)− h1u(l,t) (упруго закрепленные концы (рис. 9 в)). Числа h0 , h1 должны быть положительными,

если положение покоя есть положение устойчивого равновесия.

б)

в)

Рис.9 Ограничившись для простоты случаем струны с

закрепленными концами, приходим к следующей задаче: найти решение u(x,t) уравнения

	∂2u		∂		∂u
ρ(x)=	∂t2	=		p(x)	− q(x)u , t > 0	, 0	< x < l ,	(1)
ρ(x)=		=		p(x)	− q(x)u , t > 0	, 0	< x < l ,	(1)
			∂x		∂x
удовлетворяющее граничным условиям
			u \|x=0 = 0 , u \|x=l = 0 , t ≥ 0 ,					(2)
					55

и начальным условиям
u \|	=ϕ	0	(x), ∂u	=ϕ (x), 0 < x < l ,	(3)

t =0			∂t	1
				t =0

Будем решать эту задачу методом Фурье.

1. Ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде

произведения

u(x,t)= T (t)X (x).

(4)

Подставляя u(x,t) в форме (4) в уравнение (1), получим

T (t)

∂

∂X

− q(x)X (x)T (t)= ρ(x)X (x)T

(t)

p(x)

или

∂x

′′

∂

∂X

p(x)

− q(x)X (x)

′′

∂x

T (t) .

(5)

p(x)X (x)

Левая часть последнего

равенства

зависит

только

от

x , а

правая часть — только от t и равенство возможно лишь тогда, когда общая величина отношений (5) будет постоянной. Обозначим эту постоянную через ( − λ ). Тогда из равенства (5) получим два обыкновенных дифференциальных уравнения

		′′		,	(6)
		T	(t)+ λT (t)= 0
∂		∂X
	p(x)		−(λρ(x)− q(x))X (x)= 0 .		(7)

∂x		∂x

Чтобы получить нетривиальные решения уравнения (1) вида (4) , удовлетворяющие граничным условиям (2), необходимо, чтобы функция X (x) была нетривиальным

решением уравнения (7), удовлетворяющим граничным условиям

X (0)= 0 , X (l)= 0 .

(8)

Как мы уже видели, эта задача имеет отличное от тождественного нуля решение не при всяком λ .

Рассмотрим задачу Штурма—Лиувилля о собственных значениях: найти такие значения параметра λ , при которых существуют нетривиальные решения уравнения (7), удовлетворяющие граничным условиям (8), а также сами эти решения.

Те значения параметра λ , при которых задача (7)-(8) имеет нетривиальное решение, называются собственными значениями (числами), а сами эти решения — собственными функциями, отвечающими данному собственному значению. Совокупность всех собственных значений называется спектром данной задачи.

Всилу однородности уравнения (7) и граничных условий

(8)собственные функции определяются с точностью до постоянного множителя. Выберем этот множитель так, чтобы

∫0l ρ(x)Xk2 (x)dx =1.

(9)

Собственные функции, удовлетворяющие условию (9), будем называть нормированными с весом ρ(x).

Установим некоторые общие свойства собственных значений и собственных функций задачи Штурма—Лиувилля.

Теорема 3. Каждому собственному значению с точностью до постоянного множителя отвечает лишь одна собственная функция.

В самом деле, пусть существуют две собственные функции X1(x) и X 2 (x), отвечающие одному и тому же

собственному значению λ0 , т. е. удовлетворяющие

дифференциальному	уравнению (7)		при одном и том				же
λ = λ0 . Так как по предположению			X1(0)= 0 ,		X2 (0)	= 0 ,	то
определитель Вронского				(x)
	W (x)=	X1(x)	X2
		X1(x)	X2
		X1′(x) X2′		(x)
решений X1(x) и	X 2 (x)	уравнения		(7) в	точке	x = 0
	57

обращается в нуль и, следовательно, решения X1(x) и X 2 (x)

линейно зависимы.

Теорема 4. Собственные функции, отвечающие различным

собственным значениям, ортогональны на отрезке [0,l] с весом

ρ(x),

∫0l ρ(x)Xm (x)Xn (x)dx = 0 ,

где Xm (x), Xn (x) — собственные функции, соответствующие различным собственным значениям λm и λn .

Предварительно установим одно предложение, имеющее самостоятельный интерес. Введем так называемый оператор Штурма— Лиувилля

	∂		∂y
Ly ≡		p(x)		− q(x)y	(11)

′	∂x		∂x
					Будем
( p(x), p (x),q(x) C[0,l], p(x)≥ 0,q(x)≥ 0 на [0,l]).

рассматривать этот оператор на множестве C&2 [0,l] функций, дважды непрерывно дифференцируемых на [0,l] и удовлетворяющих граничным условиям y(0)= y(1)= 0 :

C&2 [0,l]= {y(x)| y(x) C2 [0,l]; y(0)= y(l)= 0}.

Лемма. Оператор Штурма— Лиувилля (11) на C&2 [0,l] является симметрическим:

(Lu,v)= (u, Lv) (здесь u(x),v(x) C&2 [0,l]; (f , g) = ∫0l f (x)g(x)dx ).

В самом деле,
l	∂			∂u
(Lu,v)= ∫0		p(x)					− q(x)u v(x)dx =

	∂x			∂x
l			l ∂						∂u
= −∫0 q(x)v(x)udx + ∫0						p(x)			vdx .

					∂x				∂x
Интегрируя		по	частям					последний интеграл справа и

принимая во внимание, что v |x=0 = v |x=l = 0 , найдем

(Lu,v)= −∫0l q(x)uvdx − ∫0l p(x)∂∂ux ∂∂vx dx .

Вновь интегрируя по частям второе слагаемое справа и учитывая, что u |x=0 = u |x=l = 0 , получим

(Lu,v)= −∫0 q(x)uvdx + ∫0

p(x)

udx =

= ∫0 u

p(x)

− q(x)v dx = (u, Lv).

Обратимся к доказательству теоремы. Запишем уравнение

(7) в виде

p(x)

− q(x)X (x)= −λρ(x)X (x)

(12)

и обозначим через L[X

] оператор, стоящий в левой части (12).

Это — оператор Штурма—Лиувилля. На множестве собственных функций Xk (x) задачи (7)-(8) это

симметрический оператор.

Пусть Xm (x) — собственная функция задачи (7)-(8), отвечающая собственному значению λm , а Xn (x) —

собственная функция, отвечающая собственному значению λn ,
(λn ≠ λm ). Тогда имеют место тождества
L[Xm (x)]= −λm ρ(x)Xm (x),						(0 < x	< l).
L[X	n	(x)]= −λ ρ(x)X		n	(x)
		n						Xm (x) и
Умножим первое тождество на			Xn (x), второе — на
проинтегрируем результаты по х от 0 до l. Получим
	(L[Xm ], Xn )= −λm (ρXm , Xn ),							(13)
	(L[Xn ], Xm )= −λn (ρXn , Xm ).							(14)

Замечая, что

(L[Xm ], Xn )= (Xm , L[Xn ])= (L[Xn ], Xm ),

и вычитая равенства (13) и (14) почленно, найдем
			0 = (λn − λm )(ρXm , Xn ),
откуда, при λn ≠ λm , следует, что (ρXm , Xn )= 0 , или, что то же
		∫0l ρ(x)Xm (x)Xn (x)dx = 0 (λm ≠ λn ).
Так,	в	частном		случае		однородной	струны
(ρ = p =1, q = 0),			закрепленной		на	концах, собственные
функции	Xn (x)= sin nπ x			(n =1,2,...) образуют ортогональную
			l
систему функций на отрезке [0,l],
		l	nπ	mπ		= 0 , (m ≠ n)
		∫0 sin l		xsin l	xdx	= 0 , (m ≠ n)
Теорема		5.	Все	собственные значения			(7)-(8)

действительны.

В самом деле, допустим, что существует комплексное

собственное	значение		λ =α + iβ ,		β ≠ 0 ,	которому отвечает
собственная	функция			X (x)= u(x)+ iv(x).		Тогда	комплексно
сопряженное	число			=α −iβ	также	будет	собственным
		λ

значением, а функция X (x), комплексно сопряженная с X (x),

будет соответствующей собственной функцией, поскольку коэффициенты уравнения (7) и граничные условия (8) — действительные. Из условия ортогональности собственных функций, отвечающих различным собственным значениям, следует

∫0l ρ(x)X (x)

(x)dx = ∫0l ρ(x)

X (x)

2 dx = 0 ,

откуда

X (x)≡ 0 ,

т. е. комплексное число

не

является

собственным значением.

ρ(x)> 0 , q(x)≥ 0

Теорема 6. Если p(x)> 0 ,

на отрезке

[0,l],

то все

собственные

значения

задачи

(7)-(8)

положительные.

Всамом деле, пусть λk — собственное значение, a Xk (x)

—соответствующая собственная функция, нормированная с весом ρ(x). Тогда справедливо тождество

ρ(x)

− q(x)X

(x)≡ −λ ρ(x)X

(x).

Умножая обе части тождества на Xk (x), интегрируя результат

по х от 0 до l

и принимая во внимание, что ∫0l ρ(x)Xk2 (x)dx =1,

получим

l d

∫0

q(x)X 2

(x)dx −

ρ(x)

(x)dx .

∫0 dx

Интегрируя по частям второе слагаемое справа, придем к равенству

q(x)X 2

(x)dx +

(15)

∫0

ρ(x)

k dx .

dXk

Производная

≠ 0 , так

как

противном

случае

Xk (x)≡ const

из

граничных

условий

(8)

мы имели бы

Xk (x)≡ 0 , что исключено. Таким образом, правая часть (15)

положительна, откуда следует, что все собственные значения λk задачи (7)-(8) положительны.

Теорема 7. У задачи (7)-(8) существует счетное множество

собственных значений
λ < λ < ... < λ	n	< ...,	lim λ	n	= +∞ ,
1 2	n		n→∞	n

которым отвечают собственные функции

X1(x), X2 (x), …, Xn (x), … .

Продолжим описание метода Фурье.

2. Обратимся к дифференциальному уравнению (6). Его общее решение при λ = λk > 0 имеет вид

Tk (t)= Ak cos λk t + Bk sin λk t ,

где Ak , Bk — произвольные постоянные. Каждая функция

uk (x,t)=Tk (t)Xk (x)= (Ak cos λk t + Bk sin λk t)Xk (x)

будет решением уравнения (1), удовлетворяющим граничным условиям (2).

3. Составим формальный ряд

u(x,t)= ∑∞ (Tk (t)+ Ak cos λk t + Bk sin λk t)Xk (x). (16)

k =1

Если этот ряд, вместе с рядами, полученными из него двукратным почленным дифференцированием по x и по t , сходится равномерно, то его сумма u(x,t) будет решением

уравнения (1), удовлетворяющим граничным условиям (2). Для выполнения начальных условий (3) необходимо,

чтобы

			∞
	u \|t =0 =ϕ0 (x)= ∑Ak Xk (x),			(17)
			k =1
∂u			∞
			∞
			=ϕ1(x)= ∑Bk λk Xk (x).	(18)
∂t		t =0	k =1
∂t		t =0	k =1

Таким образом, мы пришли к задаче о разложении произвольной функции в ряд Фурье по собственным функциям Xk (x) граничной задачи (7)-(8). Предполагая, что ряды (17) и

(18) сходятся равномерно, можно найти коэффициенты Ak и Bk , умножив обе части равенства (17) и (18) на ρ(x)Xn (x) и

проинтегрировав по x в пределах от 0 до l. Считая функции Xk (x) ортонормированными с весом ρ(x) на отрезке [0,l],

получим для коэффициентов Фурье функций ϕ0 (x) и ϕ1(x) по системе {Xk (x)} следующие выражения:

An = ∫0l ρ(x)ϕ0 (x)Xn (x)dx , Bn = 1λ	∫0l ρ(x)ϕ1(x)Xn (x)dx
	n

(n =1,2,...).

При нахождении коэффициентов An и Bn мы опираемся на

теорему разложения Стеклова.

Теорема 8. Всякая дважды непрерывно дифференцируемая функция F(x), удовлетворяющая граничным условиям

задачи, может быть разложена в абсолютно и равномерно
сходящийся ряд по собственным функциям Xk (x)	этой задачи,
∞
F(x)= ∑cn Xn (x),
n=1
где
cn = ∫0l ρ(x)F(x)Xn (x)dx ,
а Xn (x) (n =1,2,...) — нормированные с	весом	ρ(x)
собственные функции.
Подставим найденные значения коэффициентов An		и Bn в

ряд (16) и, если ряд (16) и ряды, полученные из него двукратным почленным дифференцированием по х и по t, сходятся равномерно, получим решение u(x,t) смешанной

задачи (1)-(3).

Замечание. Мы рассмотрели случай простейших граничных условий u(0,t)= u(l,t)= 0 . Несколько изменяя

приведенные выше рассуждения, можно доказать аналогичные свойства собственных значений и собственных функций более общей однородной краевой задачи

αu(0,t)+ βux (0,t)= 0 , γu(l,t)+δux (l,t)= 0

(α2 + β2 ≠ 0,γ 2 +δ 2 ≠ 0).

8. Единственность решения смешанной задачи

Теорема 9. Решение смешанной задачи для вынужденных

колебаний однородной струны:
∂2u	= a2 ∂2u				+ f (x,t), t > 0 , 0 < x < l ,
∂t2			∂x2
u(0,t)=ψ1(t), u(l,t)=ψ2 (t), t ≥ 0 ,
u \|	=0	=ϕ	0	(x), ∂u			=ϕ (x), 0 < x < l ,

t					∂t		1
единственно.						t =0


Допустим, что существуют два решения u1(x,t) и
задачи (1)-(3). Тогда				разность			v(x,t)= u1(x,t)−u2 (x,t

решений будет удовлетворять однородному уравнению

∂2u = a2 ∂2u , t > 0 , 0 < x < l ,

∂t2 ∂x2

нулевым граничным условиям

v(0,t) = 0 , v(l,t)= 0 , t ≥ 0 ,

и нулевым начальным условиям

v(x,0)= 0 , vt (x,0)= 0 , 0 ≤ x ≤ l .

(1)

(2)

(3)

u2 (x,t) ) этих

(4)

(5)

(6)

Покажем, что соотношениям (4)-(6) удовлетворяет лишь функция, тождественно равная нулю.

Рассмотрим функцию

	1	l	∂v	2		2	∂v	2
E(t)=	1		∂v		+ a	2	∂v		dx	(7)
E(t)=	2				+ a				dx	(7)
	2	∫0	∂t				∂x

и покажем, что при условиях (4)-(6) она не зависит от времени t. Взяв производную по t, получаем

dE(t)

∂v ∂

v2 + a2 ∂v

∂

∫0

∂t ∂t

∂x ∂x∂t

∂v ∂2v

+ a

∂v ∂v

x=l

= −a

l ∂v ∂2v

dx =

= ∫0

∂t ∂t

∫0

∂t

x=0

l	∂v	∂	2	v2	− a2 ∂	2	v2
= ∫0	∂v	∂		v2	− a2 ∂		v2	dx ≡ 0	,
	∂t	∂t			∂x

так как внеинтегральное слагаемое обращается в нуль в силу

условий (5),

∂2v

− a2 ∂2v

≡ 0 ,

так

как

v(x,t)

—

решение

уравнения (4).

∂t2

∂x2

Итак,

dE(t)

≡ 0 , т.е.

E(t)≡ const .

Учитывая

начальные

условия (6), получаем

∂v

(0)=

− a

dx = 0 ,

∂t

∂x

∫0

t =0

и,

следовательно,

E(t)≡ 0 .

Из того, что интеграл от

непрерывной неотрицательно функции равен нулю,

∂v

∫0

+ a

= 0 ,

∂t

∂x

следует, что

∂v 2

+ a

∂v

≡ 0

∂t

откуда ∂v

∂v

∂x

≡ 0

≡ 0 , так что v(x,t)≡ const . В силу первого

∂t

∂x

v(x,0)= 0 ,

значит, v(x,t)≡ 0 , т. е.

из

начальных условий

u1(x,t)≡ u2 (x,t).

Интеграл (7) можно переписать в виде a

∂v

+ a

dx =

ρt

Tvx

dx .

2 ∫0

∂t

∂x

ρ ∫0

Величина

∫0l 12 ρvt2dx

является кинетической энергией струны в момент времени t , а

∫0l 12 Tvx2dx

— ее потенциальная энергия, так что функция E(t) с точностью до постоянного множителя ρ−1 = const выражает полную энергию струны. Равенство E(t)≡ 0 является

математическим выражением закона сохранения энергии для свободных колебаний любой физической природы при нулевых граничных условиях, т. е. когда нет притока или рассеивания энергии в процессе колебаний. Неоднородность в граничных условиях и неоднородность в уравнении означает наличие постоянно действующих факторов, подводящих или рассеивающих энергию. Неоднородность в начальных условиях означает, что в начальный момент процесс обладал некоторым запасом энергии, который он и сохраняет в течение всего колебания.

Изложенный метод доказательства единственности решения смешанной задачи называется энергетическим и широко используется при установлении различных теорем единственности.

9. Колебания круглой мембраны

Метод Фурье разделения переменных применяется также при изучении колебаний ограниченных тел, плоских или объемных. Рассмотрим в качестве примера задачу о свободных колебаниях под действием начальных возмущений однородной круглой мембраны радиуса r0 с центром в начале

координат, закрепленной по краю.

Уравнение колебаний мембраны имеет вид

∂2u			2	∂2u		∂2u
	2	= a			2 +		2
∂t				∂x		∂y

Введем полярные координаты r , ϕ . Тогда отклонение точек мембраны будет функцией полярных координат r , ϕ и времени t , u = u(r,ϕ,t). Пользуясь выражением для оператора

Лапласа u ≡ ∂2u + ∂2u в полярных координатах,

∂x2 ∂y2

u ≡	∂2u	+	1 ∂u	+	1 ∂2u	,

	∂r2		r ∂r		r2 ∂ϕ2

запишем уравнение колебаний мембраны в следующем виде:

∂2u

∂2u 1

∂u 1

∂2u

= a

∂t

∂r

∂ϕ

Таким образом, задача о колебаниях мембраны ставится так: найти функцию u(r,ϕ,t), удовлетворяющую уравнению

∂2u

∂2u 1 ∂u 1 ∂2u

= a

(1)

∂t

∂r

r ∂r

∂ϕ

граничным условиям

u |r =r = 0

(2)

(мембрана закреплена по краю) и начальным условиям

u |

= f (r,ϕ), ∂u

= F(r,ϕ).

(3)

t =0

∂t

t =0

Ограничимся важным частным случаем осесимметричных

колебаний, когда начальные функции

и F

не зависят от ϕ .

Ясно, что тогда в любой момент времени t > 0 величина отклонения мембраны не будет зависеть от полярного угла ϕ ,

а будет только функцией r и t , u = u(r,t). Это означает, что

при любом фиксированном t форма колеблющейся мембраны будет описываться поверхностью вращения.

При этом предположении задача сводится к отысканию решения u(r,t) уравнения

∂2u

∂u

= a

(4)

∂t

∂r

r ∂r

при граничном условии

u |r =r

= 0

(5)

и начальных условиях

u |

= f (r),

∂u

= F(r).

(6)

t =0

∂t

t =0

Применяя метод разделения переменных, будем искать нетривиальные решения уравнения (4), удовлетворяющие

граничному условию (5), в виде
u(r,t)= T (t)R(r).	(7)

Подставляя функцию u(r,t) в форме (7) в уравнение (4) и разделяя переменные, получим

′′

′

(t)

R (r)+

(r)

′′

= −λ . (λ > 0).

(8)

a2T (t)

R(r)

Равенства

(8)

приводят

двум

обыкновенным

дифференциальным уравнениям

′′

(9)

T (t)+ λa T (t)= 0 ,

R′′(r)+

r R′(r)+ λR(r)= 0 ,

(10)

R(r0 )

= 0 ,

R(0)

< +∞

(11)

(условие

R(0) < +∞ выражает

естественное требование

ограниченности решения u(r,t) в центре мембраны, т.е. при r = 0 ). Задача (10)-(11) имеет очевидное тривиальное решение R(r)≡ 0 , которое нас не устраивает.

Итак, мы пришли к задаче на собственные значения: найти

те значения параметра λ , при которых существуют нетривиальные решения задачи (10)-(11), и отыскать эти решения.

Запишем уравнение (10) в следующем виде: r2 R′′(r)+ rR′(r)+ (λr2 − 0)R(r)= 0 .

Это дифференциальное уравнение Бесселя с v = 0 . Его общее решение

R(r)= C1g0 ( λr)+ C2 N0 ( λr).

Из условия R(0) < +∞ следует, что C2 = 0 (функция

Неймана N0	( λr) → ∞). Таким образом,
	r →+0

R(r)= g0 ( λr).

Граничное условие R(r0 )= 0 дает

f0 ( λr0 )= 0 ,

откуда следует, что число λr0 должно быть одним из нулей функции Бесселя g0 (x), т.е.

λr = μk ,
где μk — нуль функции g0 (x).	Известно, что функция

g0 (x) имеет бесконечное множество положительных нулей

0 < μ1 < μ2 < ... < μn < ... ,

откуда получаем собственные значения

λn = μr0n 2 , n =1,2,...,

и соответствующие собственные функции

Rn (r)= g0 μr0n r , r =1,2,...,

задачи (10)-(11).

При λ = λn общее решение уравнения (9) имеет вид

Tn (t)= An cos arμ0 n t + Bn sin arμ0 n t .

Функция

un (r,t)= An cos arμ0 n t + Bn sin arμ0 n t g0 μr0n r

будет решением уравнения (4), удовлетворяющим граничному

условию (5). Она определяет стоячие осесимметричные волны

круглой мембраны.

Решение u(r,t) исходной задачи (4)-(6) ищем в виде

формального ряда

∞

aμn

μn

t +

Bn sin

(12)

un (r,t)= ∑ An cos

t g0

r ,

n=1

коэффициенты An и Bn

которого определяются из начальных

условий

∞

aμn

u(r,0)= f (r)= ∑An g0

r ,

(13)

n=1

∂u

= F(r)

∞

aμn

μn

∂t

= ∑

Bn g0

r ,

(14)

t =0

n=1

f (r)

и F(r)

т. е. мы приходим к разложению данных функций

в ряды по функциям Бесселя.

aμm

Нетрудно проверить, что при m ≠ n функции g0

r и

aμn

[0,r0

] с весом

r .

Известно,

что

r ортогональны на

всякая функция Ф(r) C2 (0, r0 ), удовлетворяющая граничным

условиям задачи, может быть разложена в абсолютно и равномерно сходящийся ряд Фурье—Бесселя

∞

Ф(r)= ∑cn g0

n=1

где

∫0 rФ(r)g0

r dr

cn =

(r =1,2,...).

∫0 rg0

Пользуясь этим, при достаточно гладких начальных

условиях f (r)

и F(r)

получаем для коэффициентов Фурье—

Бесселя функций f (r) и F(r) следующие формулы:

∫0 rf (r)g0

r dr

∫0 rФ(r)g0

r dr

, B =

aμ

∫0

rg0

∫0 rg0

(n =1,2,...).

Подставим найденные значения An и Bn в формулу (12).

Если при этом ряд (12) сходится равномерно, так же как и ряды, получаемые из него двукратным почленным дифференцированием по каждому из аргументов t и r , то мы получаем решение задачи (4)-(6).

10. Применение преобразований Лапласа к решению смешанной задачи

Пусть требуется найти решение u(x,t) уравнения

∂2u		= a2 ∂2u	, t > 0 , 0 < x < l ,		(1)
∂t2		∂x2
удовлетворяющее начальным условиям
u(x,0)=ϕ	0	(x), ∂u(x,0)		=ϕ (x), 0 ≤ x ≤ l ,	(2)
u(x,0)=ϕ		(x), ∂u(x,0)		=ϕ (x), 0 ≤ x ≤ l ,	(2)
		∂t		1
			71	t =0
				t =0

и граничным условиям
u(0,t)= μ1(t), u(l,t)= μ2 (t), t ≥ 0 .	(3)

Независимая переменная t изменяется от 0 до + ∞ . Применяя преобразование Лапласа по t, предположим, что

u(x,t), ∂u и

∂2u

, рассматриваемые как функции t ,

являются

∂x

∂x2

функциями-оригиналами. Пусть U (x, p) есть изображение

функции u(x,t) по Лапласу,

U (x, p)= ∫0+∞u(x,t)e− pt dt .

Так как операция дифференцирования по х и операция

интегрирования

по

преобразовании

Лапласа

перестановочны, получим

∂u

∂

∫0+∞ u(x,t)e− pt dt = ∫0+∞ ∂u e− pt dt = dU (x, p) ,

∂x

∂2u

∂2

+∞

(x,t)e

− pt

+∞ ∂2u

− pt

d 2U (x, p)

∂x2 =

∫0

= ∫0 ∂x2 e

dx2

∂x2

(здесь величина

рассматривается как параметр,

и вместо

частных производных

∂k

пишут обычные производные

d k

∂xk

d xk

k =1,2 ).

По правилу дифференцирования оригиналов имеем

∂u

= pU −u(x,0),

∂t

∂u(x,0)

∂2u

∂t2

= p U − pu(x,0)−

∂t

Отсюда, учитывая начальные условия (2) , получаем

∂u

= pU −ϕ

(x),

∂2u

(x)−ϕ

(x).

∂t

∂t2

= p U − pϕ

Пусть функции μ1(t)

и μ2 (t), фигурирующие в граничных

условиях

(3),

являются

функциями-оригиналами

μ1(t)= M1(p), μ2 (t)= M2 (p). Тогда граничные условия (3) дают

U (0, p)= ∫0+∞u(0,t)e− pt dt = M1(p), U (l, p)= ∫0+∞ u(l,t)e− pt dt =M2 (p).

Переходя к изображениям, сводим задачу (1)-(3) для уравнения с частными производными к граничной задаче для обыкновенного дифференциального уравнения:

найти решение U (x, p) уравнения

d 2U −	p2	U = −	p	ϕ		(x)−	1	ϕ (x)	(4)
							a2
dx2	a2		a2		0			1
при граничных условиях
U (0, p)= M1(p), U (l, p)= M2 (p).									(5)
Пусть U (x, p) — решение задачи (4)-(5). Тогда функция

u(x,t) (оригинал для U (x, p)) будет решением исходной

задачи (1)-(3).
Пример. Струна l закреплена на концах x = 0 и x = l .
Начальное отклонение струны определяется формулой
u(x,0)= Asin πx , A − const .
				l
Начальные скорости		отсутствуют.			Найти отклонение
u(x,t) струны при t > 0 .
Задача сводится к отысканию решения u(x,t) уравнения
∂2u	= a2 ∂2u		,	t > 0 , 0 < x < l ,		(6)
∂t2	∂x2
при начальных условиях		πx		∂u(x,0) = 0
u(x,0)= Asin		πx	,	∂u(x,0) = 0	, 0 ≤ x ≤ l ,	(7)
и граничных условиях		l		∂t
и граничных условиях				u(l,t)= 0 , t ≥ 0 .
	u(0,t)= 0 ,			u(l,t)= 0 , t ≥ 0 .		(8)
				73

Применим преобразование Лапласа по t . Пусть U (x, p) — изображение функции u(x,t),

U (x, p)= ∫0+∞u(x,t)e− pt dt .

Тогда
	∂u =	∂U	,	∂2u	= ∂2U .
	∂x	∂x		∂x2	∂x2
По правилу дифференцирования оригиналов с учетом
начальных условий (7) получаем
∂u		πx		∂2u	2	πx
∂t	= pU − Asin	l	,	∂t2	= p U − pAsin	l .

Граничные условия (8) в свою очередь дают

U (0, p)= ∫0+∞u(0,t)e− pt dt = 0 , U (l, p)= ∫0+∞ u(l,t)e− pt dt = 0 .

Таким образом, в пространстве изображений мы приходим к граничной задаче для обыкновенного дифференциального уравнения:

∂2U	−	p2		U =	Ap sin	πx	,	(9)
∂x2		a2				l
					a2
U (0, p)			=U (l, p)= 0 .					(10)

Решая уравнение (9) как линейное с постоянными коэффициентами, найдем

(x, p)= C e

e−

πx .

+ C

sin

a2π 2

Из условий (10) получаем C1 = C2 = 0 , так что

U (x, p)=

sin πx .

p2 +

a π

Оригиналом для U (x, p) является функция

u(x,t)= Acos πatl sin πlx ,

которая будет решением задачи (6) -(8).

Аналогичным приемом решаются смешанные задачи для более общих уравнений гиперболического (и параболического) типа.

Ход решения уравнения с частными производными при помощи преобразования Лапласа можно представить в виде следующей схемы (число независимых переменных n = 2 ).

В пространстве оригиналов уравнение с частными производными

+начальные условия +граничные условия

В пространстве изображений обыкновенное дифференциальное уравнение

+граничные условия

Решение в пространстве изображений

α−1

Решение исходной задачи

Рис. 10. Блок-схема метода решения уравнения с частными производными при помощи преобразования Лапласа

Упражнения

Найдите решение следующих начальных задач:

1. ∂2u = a2 ∂2u , t > 0 , − ∞ < x < +∞, u |

= e−x2 , ∂u

= cos x .

∂t2

∂x2

t =0

∂t

t =0

2. ∂2u = a

2 ∂2u , t > 0 , − ∞ < x < +∞, u |

= 0 , ∂u

∂t2

∂x2

t =

∂t

t =0

1 + x2

3. Однородная бесконечная струна возбуждена начальным отклонением, имеющим форму полуокружности:

u(x,0)= 1 − x2 , −1 ≤ x ≤1 . Начальные скорости отсутствуют.

Начертите

положение

струны

для

моментов

времени

t =

1 , t =1, t = 2 , считая для простоты а = 1.

Применяя метод Фурье разделения переменных, решите

следующие смешанные задачи:

∂2u

= a2 ∂2u

t > 0 ,

0 < x < l ,

u |x=0 = u |x=l = 0 ,

∂t2

∂x2

u |

= sin 3π x , ∂u

= 0 .

∂t

t =0

5. ∂2u = a2 ∂2u ,

t > 0 , 0 < x < l , u |

x=0

= u |

x=l

= 0 , u |

= 0 ,

∂t2

∂x2

t =0

∂u

= sin

π x .

∂t

t =0

∂2u

, t > 0 , 0 < x < π , u |

= u |

= 0 , u |

= 0 ,

∂t

∂x2

x=0

=π

t =0

∂u

= sin x .

∂t

t =0

7. ∂2u = a2 ∂2u ,

t > 0 , 0 < x < l , u |

x=0

= u

x=l

= 0 ,

u |

= 0 ,

∂t2

∂x2

t =0

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.57 Mб12903.pdf
#
15.11.20222.57 Mб12904.pdf
#
15.11.20222.57 Mб02905.pdf
#
15.11.20222.58 Mб02906.pdf
#
15.11.20222.58 Mб72909.pdf
#
15.11.20222.58 Mб102910.pdf
#
15.11.20222.59 Mб02912.pdf
#
15.11.20222.59 Mб02914.pdf
#
15.11.20222.59 Mб12915.pdf
#
15.11.20222.6 Mб22916.pdf
#
15.11.20222.6 Mб02917.pdf