
- •Упражнения
- •Ответы
- •Приведем пример Адамара некорректно поставленной задачи. Рассмотрим задачу Коши: найти решение уравнения Лапласа
- •III. Уравнения параболического типа
- •Примеры библиографического описания
- •Описание изданий под редакцией
- •Описание статьи из газеты
- •Описание стандартов
- •III. Уравнения параболического типа ..........................

И.Н. Пантелеев
ОСНОВЫ МАТЕМАТИЧЕСКИХ МЕТОДОВ РЕШЕНИЯ ПРИКЛАДНЫХ ЗАДАЧ
Учебное пособие
∂2u |
|
2 |
|
∂2u |
∂2u ∂2u |
|
|||||||
|
|
= a |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 + |
|
2 + |
|
2 |
|||||
∂t |
|
|
∂ x |
∂ y |
∂ z |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
Воронеж 2005
Воронежский государственный технический университет
И.Н. Пантелеев
ОСНОВЫ МАТЕМАТИЧЕСКИХ МЕТОДОВ РЕШЕНИЯ ПРИКЛАДНЫХ ЗАДАЧ
Утверждено редакционно-издательским советом университета
в качестве учебного пособия
Воронеж 2005
УДК 681.3.06(075)
Пантелеев И.Н. Основы математических методов решения прикладных задач: Учеб. пособие. Воронеж: Воронеж. гос.
техн. ун-т, 2005. 310 с.
Учебное пособие подготовлено как справочное руководство для выполнения курсовой работы и ориентировано на самостоятельное изучение методов решения дифференциальных уравнений с частными производными. Рассмотрены основные дифференциальные уравнения гиперболического, параболического и эллиптического типа. Приведены примеры решения уравнений Лапласа, Гельмгольца, Пуассона для различной геометрии. Отмечены особенности использования MatLab для численного решения дифференциальных уравнений с частными производными.
Издание предназначено для студентов инженерных специальностей вузов при изучении раздела «Уравнения матфизики» в курсе «Высшая математика».
Учебное пособие подготовлено на магнитном носителе в редакторе Adobe Acrobat и содержится в файле
"VM_UrMat.pdf".
Табл. 2. Ил. 39. Библиогр.: 28 назв.
Рецензенты: кафедра математики и физики Воронежского Военного института радиоэлектроники (зав. кафедрой канд. физ.-мат.наук, проф. А.В. Паршин);
канд. физ.-мат. наук, доц. В.И. Ковалевский
©Пантелеев И.Н., 2005
©Оформление. ГОУВПО «Воронежский государственный технический университет», 2005
Введение
Наиболее важным результатом изучения курса ″Высшая математика″ для студентов технических специальностей является умение формулировать математические модели реальных объектов и решать прикладные задачи с использованием, например, уравнений математической физики. Это служит необходимым условием успешной профессиональной работы выпускников, выбравших для себя в дальнейшем участие в научно-исследовательских и проектно-конструкторских разработках.
Выполнение курсовой работы по высшей математике, предусмотренное учебным планом для специальностей ЧС и БЖ, нацелено на усиление связи обучения студентов с практической деятельностью, направленной на совершенствование и создание новых методов и систем защиты человека и среды обитания, проведение анализа негативных факторов и техногенного риска современного производства и технических систем, участие в исследованиях по воздействию антропогенных факторов и стихийных явлений на промышленные объекты, осуществление развития новых методов повышения надежности и устойчивости технических объектов, локализации и ликвидации последствий аварий и катастроф. В процессе работы над курсовой работой студент не только закрепляет и углубляет теоретические знания, полученные на лекциях и на практических занятиях, но и учится применять их при постановке и решении конкретных прикладных задач. Цель курсовой работы - подготовить студента к самостоятельному проведению операционного исследования, основными этапами которого являются построение математической модели, решение задачи с использованием как аналитических, так и численных методов, а также проведение анализа полученных результатов.
Данное учебное пособие подготовлено как справочное руководство для выполнения курсовой работы и ориентировано на самостоятельное изучение методов решения дифференциальных уравнений с частными производными. В пособии рассмотрены физические задачи, приводящие к дифференциальным уравнениям в частных производных, колебательные процессы, теплопроводность и диффузия, стационарные процессы. Первые четыре главы посвящены общим сведениям о дифференциальных уравнениях с частными производными. Рассмотрены особенности решения дифференциальных уравнений гиперболического, параболического и эллиптического типа. Пятая глава посвящена методам решения уравнений математической физики. Приведены примеры решения уравнений Лапласа, Гельмгольца, Пуассона для различной геометрии. Шестая глава отражает особенности использования MatLab для численного решения дифференциальных уравнений с частными производными. Рассмотрены явные и неявные разностные схемы для уравнений параболического и эллиптического типов, а также метод Монте-Карло. Проведен анализ численных методов решения интегральных уравнений Фредгольма и Вольтерра. В приложении даются рекомендации по оформлению курсовой работы.
4
3
I. Общие сведения о дифференциальных уравнениях с частными производными 1. Основные понятия. Примеры
Дифференциальным уравнением с частными производными называются уравнения вида
|
|
|
∂u |
|
∂u |
|
|
∂mu |
|
|
|
|
|
|
, x2 |
,..., xn ,u, |
|
|
|
|
|
|
|
|
|
= 0, |
(1) |
∂x |
,..., ∂x |
,..., ∂xk1 |
∂xk2 |
|
|
||||||||
F x1 |
...∂xkn |
||||||||||||
|
|
|
1 |
|
n |
1 |
2 |
|
n |
|
|
|
|
связывающее независимые переменные x1, x2 ,..., xn , искомую функцию u = u(x1, x2 ,..., xn ) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь k1, k2 ,..., kn —
неотрицательные целые числа, такие, что k1 + k2 +... + kn = m .
Порядком дифференциального уравнения называется наивысший порядок входящих в уравнение частных производных. Так, если x, y — независимые переменные, u = u(x, y) — искомая функция, то
|
|
y ∂u |
− x |
∂u |
= 0 |
|
|
||
|
|
∂x |
|
∂y |
|
|
|
|
|
—дифференциальное уравнение 1-го порядка; |
|
||||||||
∂2u |
− |
∂2u |
= 0 , |
∂u |
− |
∂2u |
= e |
u |
|
∂x2 |
∂y2 |
∂x |
∂y2 |
|
|||||
|
|
|
|
|
|
||||
—дифференциальные уравнения 2-го порядка.
Для упрощения записи пользуются также следующими
обозначениями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u |
x |
≡ |
∂u |
, |
u |
y |
≡ |
∂u |
, u |
xx |
≡ |
∂2u |
, |
u |
xy |
≡ |
∂2u |
,.... |
|
∂x |
∂y |
∂x2 |
∂x∂y |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пусть имеем дифференциальное уравнение с частными производными (1) порядка m. Обозначим через Cm (D)
множество функций, непрерывных в области D вместе со всеми производнымидопорядкаm включительно.
Определение. Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных
x1, x2 ,..., xn |
называется |
всякая |
функция |
u = u(x1, x2 ,...xn ) Cm (D), такая, что подстановка этой функции
и ее производных в уравнение (1) обращает последнее в тождество по x1, x2 ,..., xn в области D.
Пример 1. Найти решение u = u(x, y) уравнения
∂u = 0 . |
(2) |
∂x |
|
Равенство (2) означает, что искомая функция u не зависит |
|
от x , но может быть любой функцией от у, |
|
u =ϕ(y). |
(3) |
Таким образом, решение (3) уравнения (2) содержит одну
произвольную функцию. Это — общее решение уравнения (2). |
||||||
Пример 2. Найти решение u = u(x, y) уравнения |
|
|
||||
|
|
|
∂2u |
= 0 . |
|
(4) |
|
|
|
∂x∂y |
|
||
|
|
|
|
|
|
|
Положим |
∂u |
=υ . Тогда уравнение (4) примет вид |
∂υ |
= 0 . |
||
|
∂y |
|
|
|
∂x |
|
Его общим решением будет произвольная функция υ = ω(y).
Поскольку |
υ = ∂u , приходим к уравнению |
∂u |
= ω(y). |
|
∂y |
∂y |
|
Интегрируя по у (считая х параметром), получим |
|
|
|
где g(x) |
u(x, y)= ∫ ω(y)dy + g(x), |
ω(y) — |
|
— произвольная функция. Так как |
|||
произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f (y). В результате получим решение уравнения (4) в виде
u(x, y)= f (y)+ g(x) (5) ( f (y), g(x) — произвольные дифференцируемые функции).
6
5
Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g .
Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, даже пусты.
Пример 3. Множество действительных решений уравнения
|
|
∂u 2 |
|
∂u 2 |
||
|
|
|
+ |
|
= 0 |
|
|
|
∂x |
|
|
∂y |
|
исчерпывается функцией u(x, y) |
= const , а уравнение |
|||||
∂u 2 |
|
∂u 2 |
+1 = 0 |
|||
|
|
|
+ |
|
|
|
|
∂x |
|
∂y |
|
||
вовсе не имеет действительных решений.
Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т. е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.
2. Линейные дифференциальные уравнения с частными производными. Свойства их решений
Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.
7
Пример 1.
∂2u = x2 ∂2u + e−x2 ∂x2 ∂y2
— линейное уравнение; уравнения
y |
∂u |
− x |
∂u |
+ u |
2 |
= 0 , u |
∂2u |
+ |
∂u |
= x |
2 |
y |
∂x |
∂y |
|
∂x2 |
∂y |
|
|||||||
|
|
|
|
|
|
|
|
|
— нелинейные.
Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных x, y в общем случае
имеет вид |
|
|
|
|
|
A(x, y)∂2u |
+ 2B(x, y) |
∂2u |
+ C(x, y)∂2u |
+ |
|
∂x∂y |
|||||
∂x2 |
|
∂y2 |
(1) |
||
+ a(x, y)∂u |
|
|
|
||
+ b(x, y)∂u + c(x, y)u = f (x, y), |
|||||
∂x |
∂y |
|
|
||
где A(x, y), B(x, y),...,c(x, y), f (x, y) |
— функции |
переменных |
|||
(x, y), заданные в некоторой области D плоскости xOy . Если f (x, y)≡ 0 в D, то уравнение (1) называется однородным, в
противном случае — неоднородным. |
|
Обозначив левую часть уравнения (1) через L[u], запишем |
|
(1) в виде |
|
L[u]= f (x, y). |
(2) |
Соответствующее однородное уравнение запишется так: |
|
L[u]= 0 . |
(3) |
Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C2 (D) функций u = u(x, y).
Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.
8
Теорема 1. Если u(x, y) есть решение линейного однородного уравнения (3), то cu(x, y), где c — любая постоянная, есть также решение уравнения (3).
Теорема 2. Если u1 (x, y) и u2 (x, y) — решения линейного однородного уравнения (3), то сумма u1(x, y)+u2 (x, y) есть также решение этого уравнения.
Следствие. Если каждая из функций u1(x, y),u2 (x, y),...,uk (x, y) является решением уравнения (3), то
линейная комбинация
c1u1(x, y)+ c2u2 (x, y)+... + ckuk (x, y),
где c1,c2 ,...,ck — произвольные постоянные, также является
решением этого уравнения.
В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.
Пример 2. Уравнение
∂∂uy = 0
имеет общее решение u =ϕ(x), так что решениями его будут, например, функции 1, x,..., xn ,... .
Всоответствии с этим в линейных задачах для уравнений
счастными производными нам придется иметь дело не только
слинейными комбинациями конечного числа решений, но и с
∞
рядами ∑cnun (x, y), членами которых являются произведения
n=1
постоянных cn на частные решения un (x, y) дифференциального уравнения.
Возможны случаи, когда функция u(x, y,λ) при всех значениях параметра λ из некоторого интервала (λ0 ,λ1 ),
конечного или бесконечного, является решением уравнения
(3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ . Если теперь взять функцию C(λ) такую, что первые и вторые производные интеграла
U (x, y)= ∫λλ01 C(λ)u(x, y,λ)dλ
по x и по y могут быть получены с помощью
дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения
L[u]= f |
(4) |
|
справедливы следующие предложения. |
|
|
Теорема 3. Если u(x, y) |
есть решение |
линейного |
неоднородного уравнения (4), a υ(x, y) — решение
соответствующего однородного уравнения (3), то сумма u +υ есть решение неоднородного уравнения (4).
Теорема 4. (принцип суперпозиции). Если u1(x, y) — решение уравнения L[u]= f1 , a u2 (x, y) — решение уравнения L[u]= f2 , то u1 + u2 — решение уравнения L[u]= f1 + f2 .
3. Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными
Определение. Линейное дифференциальное уравнение второго порядка
10
9

A(x, y)∂2u |
+ 2B(x, y) |
|
∂2u |
+ C(x, y)∂2u |
+ |
||
∂x∂y |
|||||||
∂x2 |
|
|
∂y2 |
(1) |
|||
+ a(x, y)∂u |
|
|
|
|
|
||
+ b(x, y)∂u + c(x, y)u = f (x, y) |
|||||||
∂x |
|
∂y |
|
|
|||
в некоторой области Ω на плоскости xOy называется |
|||||||
1) гиперболическим в Ω, если |
|
|
|
||||
|
= B2 − AC > 0 в Ω ; |
|
|||||
2) параболическим в Ω , если |
|
|
|
||||
|
= B2 − AC ≡ 0 в Ω; |
|
|||||
3) эллиптическим в Ω , если |
|
|
|
|
|
||
|
= B2 − AC < 0 в Ω . |
|
|||||
Пользуясь этим определением, легко проверить, что |
|||||||
уравнения |
|
|
|
|
|
|
|
|
∂2u |
= |
∂2u |
|
|
||
|
∂x2 |
∂y2 |
|
|
|||
|
|
|
|
|
|||
и
∂2u = 0 ∂x∂y
— гиперболические при всех x и у, уравнение
∂u = ∂2u ∂x ∂y2
— параболическое при всех х и у, а уравнение
∂2u + ∂2u = 0 ∂x2 ∂y2
— эллиптическое при всех х и у. Уравнение
y∂2u + ∂2u = 0 ∂x2 ∂y2
—эллиптическое при y > 0 , параболическое на линии y = 0 и гиперболическое в полуплоскости y < 0 .
Можно показать, что при определенных условиях на коэффициенты уравнения (1) существует не особая замена независимых переменных
ξ =ϕ(x, y), η =ψ (x, y) (ϕ,ψ C2 ),
с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.
Уравнение гиперболического типа ( |
|
|
> 0) преобразуется к |
||||||||||||||||||||||||||
виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∂2u |
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
|
∂u |
|
|
|
|||||||||
|
|
|
|
|
|
|
= F ξ ,η, u, |
|
|
|
|
|
|
, |
|
|
|
|
|
|
, |
||||||||
|
∂ξ∂η |
|
∂ |
ξ |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂η |
|||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∂2u |
|
∂2u |
|
|
|
|
|
|
|
∂u |
|
|
|
∂u |
|
|
|||||||||||
|
|
|
|
|
− |
|
|
|
|
= |
Ф ξ,η |
,u, |
|
|
|
|
|
, |
|
|
|
|
|
||||||
|
|
∂ξ |
2 |
|
∂η |
2 |
∂ξ |
|
|
∂η |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(два канонических вида уравнений гиперболического |
|||||||||||||||||||||||||||||
типа). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≡ 0) преобразуется к |
|||||||||||
Уравнение параболического типа ( |
|
|
|||||||||||||||||||||||||||
виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∂2u |
|
|
|
|
∂u |
|
∂u |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
= Ф |
ξ,η,u, |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∂η |
2 |
∂ξ |
∂η |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(канонический вид уравнения параболического типа). |
|||||||||||||||||||||||||||||
Уравнение эллиптического типа |
|
( |
|
|
< 0) преобразуется к |
||||||||||||||||||||||||
виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∂2u |
|
∂2u |
|
|
|
|
|
|
|
∂u |
|
|
|
∂u |
|
|
|||||||||||
|
|
|
|
+ |
|
|
|
|
|
= |
Ф ξ,η,u, |
|
|
|
|
|
, |
|
|
|
|
||||||||
|
|
∂ξ |
2 |
|
∂η |
2 |
|
∂ξ |
|
∂η |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции
u , ее первых производных |
∂u |
, |
∂u |
и независимых |
|
∂ξ |
∂η |
||||
|
|
|
|||
12 |
|
|
|
|
11
переменных ξ , η . Вид функций F и Ф определяется исходным
уравнением (1).
В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.
Как правило, приведение уравнения (1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки M0 (x0 , y0 ).
Когда число n независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при n = 4 простейшая каноническая форма таких уравнений имеет вид
∂2u − ∂2u − ∂2u − ∂2u = 0 (гиперболический тип),
∂t2 ∂x2 ∂y2 ∂z2
∂2u − ∂2u − ∂2u − ∂2u = 0 (параболический тип),
∂t ∂x2 ∂y2 ∂z2
∂2u + ∂2u + ∂2u + ∂2u = 0 (эллиптический тип).
∂t2 ∂x2 ∂y2 ∂z2
Здесь u = u(x, y, z,t).
Замечание. В общем случае, когда число независимых переменных больше двух, приведение линейного уравнения с переменными коэффициентами
∞ |
∂2u |
|
∞ |
∂2u |
|
|
∑aij (x1, x2 ,..., xn ) |
|
|
|
+ ∑bi (x1, x2 ,..., xn ) |
∂x |
+ |
∂x |
∂x |
j |
||||
ij =1 |
i |
|
i =1 |
i |
|
|
+ c(x1, x2 ,..., xn )u = f (x1, x2 ,..., xn )
к каноническому виду возможно только в данной точке M0 (x10 , x20 ,..., xn0 ) и невозможно в любой сколь угодно малой
окрестности этой точки.
Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким
уравнениям приводит большое количество различных физических задач.
Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение):
|
|
|
∂2u |
= a2 ∂2u |
, u = u(x,t) |
(2) |
|
|
|
∂t2 |
∂x2 |
|
|
|
Здесь х |
— пространственная координата, t |
— время, |
|||
a2 = |
T |
, где |
Т — натяжение |
струны, ρ — ее |
линейная |
|
|
ρ |
|
|
|
|
|
плотность.
Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
|
|
|
∂u |
= a2 ∂2u |
, u = u(x,t) |
(3) |
|
|
|
k |
∂t |
∂x2 |
|
|
|
Здесь |
a2 = |
, где ρ |
— плотность среды, с |
— удельная |
|||
cρ |
|||||||
|
|
|
|
|
|
||
теплоемкость, k — коэффициент теплопроводности. Наконец, установившиеся процессы, когда искомая
функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
u = |
∂2u |
+ |
∂2u |
= 0 , u = u(x,t). |
(4) |
|
∂x2 |
|
∂y2 |
|
|
Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция u(x,t) вида
u(x,t)=ϕ(x − at)+ψ (x + at), 14
13

где ϕ(ξ),ψ (η) C2 .
Можно показать, что решениями уравнения (3) являются функции вида
u(x,t,λ)= Ae−a2 λ2t sin(λx + a)
(А, а — произвольные постоянные, λ — числовой параметр).
Интегрируя решение |
u(x,t, λ)= e−a2λ2t cos λx уравнения (3) |
по |
|||||||
параметру λ |
в пределах от |
− ∞ |
до |
+ ∞ , |
получим |
так |
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
U (x, t)= |
π e− |
π |
|
|||
называемое |
фундаментальное |
решение |
4a2t |
||||||
уравнения теплопроводности. |
|
|
|
|
t |
|
|
||
|
|
|
|
|
|
|
|||
Наконец, |
|
нетрудно |
убедиться, |
|
что |
||||
действительнозначные |
функции |
Pn (x, y) |
и |
Qn (x, y), |
|||||
определяемые из соотношения
(x + iy)n = Pn (x, y)+ iQn (x, y),
являются решениями уравнения Лапласа (3.4) для n = 0,1,2....
Этот последний результат есть частный случай общего утверждения, что и действительная и мнимая части аналитической функции
f (z)= u(x, y)+ iυ(x, y)
комплексного переменного z = x + iy являются решениями
уравнения Лапласа (4).
∞
В силу линейности уравнения (4) ряды ∑αn Pn (x, y) и
n=0
∞
∑βnQn (x, y) тоже будут решениями уравнения (4) , если они
n=0
сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов x, y . Таким образом, для простейшей —
канонической — формы уравнений гиперболического,
15
параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.
4. Постановка основных задач для линейных дифференциальных уравнений второго порядка
Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω , в которой процесс происходит (граничные условия). Это обусловлено не единственностью решения дифференциальных уравнений.
Пример. Общее решение уравнения
∂2u = 0 ∂x∂y
имеет вид u(x, y)= f (x)+ g(y), где f (x) и g(y) —
произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.
Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно n ):
а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область
Ω совпадает со всем пространством Rn , граничные условия отсутствуют;
б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω , начальные условия отсутствуют;
в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ Rn .
16

Упражнения
Найдите общее решение уравнения (u = u(x, y)):
1. ∂2u = ∂u .
∂y2 ∂y
2. |
∂2u |
= 2 y |
∂u |
. |
|
∂x∂y |
∂x |
||||
|
|
|
3.∂2u = ex+ y .
∂y2
4.∂2u = x + y . ∂y2
5.∂2u + 1 ∂u = 0 .
∂x∂y x ∂y
6.∂nu = 0 . ∂yn
7.Считая u = u(x, y, z), решите уравнение
∂3u |
= 0 . |
|
∂x∂y∂z |
||
|
Найдите области гиперболичности, параболичности и эллиптичности следующих уравнений:
8. ∂2u + 2 ∂2u −3 ∂2u = 0 . ∂x2 ∂x∂y ∂y2
9. ∂2u − 2x ∂2u + y ∂2u = u +1 . ∂x2 ∂x∂y ∂y2
Ответы
1. u(x, y)= Ф1(x)+Ф2 (x)ey . 2. u(x, y)= Ф1(x)ey +Ф2 (x).
3. u(x, y)= ex+ y +Ф1(x)y +Ф2 (x).
17
4. |
u(x, y)= xy2 |
+ |
y3 |
|
+Ф (x)y +Ф (x). |
|
|
||||||
|
2 |
|
x |
1 |
2 |
|
5. |
u(x, y)= Ф1(y) +Ф (x). |
|
||||
|
x |
|
|
|
2 |
|
6. |
u(x, y)=Ф (x)yn−1 |
+Ф (x)yn−2 |
+... +Ф (x). |
|||
|
1 |
|
|
|
2 |
n |
7. u(x, y, z)=Ф1(x, y)+Ф2 (x, z)+Ф3 (y, z).
8. Уравнение всюду гиперболическое.
9. В области x2 − y > 0 уравнение гиперболическое, в области x2 − y < 0 уравнение эллиптическое, кривая y = x2 состоит из точек параболичности.
II.Уравнения гиперболического типа
Куравнениям гиперболического типа приводят задачи, связанные с процессами колебаний (задача о колебаниях струны, мембраны, электромагнитных колебаниях и т. д.). Характерной особенностью процессов, описываемых гиперболическими уравнениями, является конечная скорость распространения возмущений.
Рассмотрим, например, уравнения электромагнитного поля. Законы классической теории электромагнетизма определяются системой уравнений Максвелла. В простейшем случае непроводящей, однородной и изотропной среды при отсутствии зарядов и токов эта система имеет вид
rot H = ε ∂E , |
|
(1) |
|
c ∂t |
|
|
|
rot E = − μ |
∂H |
, |
(2) |
|
|||
c ∂t |
|
|
|
div H = 0 , |
|
(3) |
|
div E = 0 . |
|
(4) |
|
Здесь E и H — векторы напряженности электрического и |
|||
магнитного полей; ε, μ — коэффициенты |
электрической и |
||
18 |
|
|
|

магнитной проницаемости ( ε, μ = const ; c — скорость света в
вакууме). |
|
|
|
|
|
|
|
|
|
|
||
Дифференцируя (1) по t , получим |
|
|
||||||||||
|
|
ε |
= |
∂2E |
= rot |
∂H |
. |
|
||||
|
|
c |
|
∂t2 |
∂t |
|
||||||
|
∂H |
|
|
|
|
|
|
|||||
Заменяя |
из (2) , найдем |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
εμ ∂2E |
= −rot rotE . |
(5) |
||||||||
|
|
c2 |
∂t2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Известно, что |
|
|
|
|
|
|
|
|
|
|
||
rot rotE = [ ,[ ,E]]= ( ,E)− 2E = grad divE − |
E . |
|||||||||||
Так как divE = 0 , то из (5) имеем |
|
|
|
|
|
|||||||
|
|
|
εμ ∂2E |
= |
E . |
|
|
|||||
|
|
|
c2 |
|
∂t2 |
|
|
|||||
|
|
|
|
|
|
|
|
|||||
Итак, для векторного поля Е получаем уравнение |
|
|||||||||||
|
|
∂2E |
|
= |
|
c |
2 |
E . |
|
|
||
|
|
∂t2 |
|
|
εμ |
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
Это одно из основных уравнений математической физики. Оно называется волновым.
Нетрудно убедиться, что векторное поле Н удовлетворяет точно такому же уравнению
∂2H = c2 H .
∂t2 εμ
Таким образом, каждая из координат Ex , Ey , Ez и Hx , H y , Hz
векторов E и H удовлетворяет в рассматриваемом простейшем случае волновому уравнению
∂2u |
|
2 |
|
∂2u |
∂2u |
∂2u |
|
|||||
|
2 |
= a |
|
|
|
2 + |
|
2 + |
|
2 |
|
(6) |
∂t |
|
|
∂x |
∂y |
∂z |
. |
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
Это уравнение гиперболического типа. Здесь a = |
c |
— |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εμ |
|
скорость, |
так |
что |
|
электромагнитные |
процессы |
|||||||||||||
распространяются в |
непроводящей |
среде |
со |
скоростью |
||||||||||||||
a = |
c |
, в частности, в вакууме (ε = μ =1) |
— со скоростью |
|||||||||||||||
|
εμ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
света с. Если u = u(x, y,t), то уравнение (6) принимает вид |
|
|||||||||||||||||
|
|
|
|
|
∂2u |
|
2 |
|
∂2u |
∂2u |
|
|
|
|
||||
|
|
|
|
|
|
2 |
= a |
|
|
|
2 + |
|
2 |
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
∂x |
∂y |
; |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в случае, когда |
u = u(x,t), получаем одномерное |
волновое |
||||||||||||||||
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
∂2u |
= a2 ∂2u |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
∂t2 |
|
|
|
∂x2 |
|
|
|
|
|
|
|
|
Именно |
с |
этого |
одномерного |
волнового |
уравнения |
||||||||||||
(уравнения колебаний струны) мы и начнем изучение гиперболических уравнений.
Струной мы называем идеально гибкую, тонкую нить, упругую лишь тогда, когда она натянута, и оказывающую сопротивление растяжению.
Пусть струна колеблется в плоскости xOu и пусть вектор смещения и в любой момент t времени перпендикулярен оси Ox . Тогда процесс колебания можно описать одной функцией u(x,t), характеризующей вертикальное перемещение струны.
Будем рассматривать малые колебания струны и пренебрегать величиной (ux )2 по сравнению с единицей. Тогда, если линейная плотность струны ρ = const и внешние силы
отсутствуют, уравнение свободных колебаний однородной струны принимает вид
∂2u |
= a2 ∂2u |
, |
∂t2 |
∂x2 |
|
20

где a2 = Tρ , а T — натяжение струны.
1. Решение задачи Коши (начальной задачи) для неограниченной струны
1.1. Метод бегущих волн. Решение Даламбера
Займемся интегрированием уравнения свободных колебаний однородной струны
∂2u |
= a2 ∂2u |
, |
(1) |
∂t2 |
∂x2 |
|
|
Здесь u(x,t) — смещение точек струны в момент времени
t от положения равновесия. При каждом фиксированном значении t график функции u = u(x,t) дает форму струны в
момент времени t.
Введем новые независимые переменные ξ,η по формулам
|
ξ = x − at , η = x + at , |
|
|
|
|
(2) |
||||||||
В переменных ξ,η уравнение (1) будет иметь вид |
|
|
|
|||||||||||
|
|
|
∂2u |
= 0 . |
|
|
|
|
|
|
|
|||
|
|
|
∂ξ∂η |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
В этом легко убедиться, вычислив производные |
∂2u |
и |
∂2u |
, |
||||||||||
∂t2 |
∂x2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
∂u ∂u ∂ξ |
∂u ∂η ∂u |
∂u |
|
|
|
|||||||||
∂x = |
|
∂x + |
|
∂x = |
|
+ |
|
, |
|
|
|
|||
∂ξ |
∂η |
∂ξ |
∂η |
|
|
|
||||||||
∂2u |
= |
∂ |
∂u |
= |
|
∂x2 |
|
|
|
||
|
|||||
|
∂x |
∂x |
|
||
∂∂ut =
|
∂2u ∂ξ |
+ |
|
∂2u |
|
∂η |
+ |
|
∂2u |
|
∂ξ |
+ |
∂u |
∂η |
= |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂ξ2 ∂x |
|
∂ξ∂η |
|
∂x |
∂η∂ξ ∂x |
∂η ∂x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= |
|
∂2u |
+ 2 |
∂2u |
|
+ |
|
∂2u |
, |
|
|
|
|
|
|
|
|
|
|||||||||
∂ξ2 |
∂η∂ξ |
|
∂η2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∂u |
∂ξ |
|
|
∂u ∂η |
|
|
|
|
∂u |
|
|
∂u |
|
|
|
|
|||||||||||
|
|
|
|
|
+ |
|
|
|
|
|
= a |
|
|
|
|
− |
|
|
|
, |
|
|
|
|
|||
∂ξ ∂t |
|
∂η ∂t |
∂η |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
∂ξ |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∂2u |
= |
∂ |
∂u |
= a |
2 |
∂2u |
− 2a |
2 |
∂2u |
+ a |
2 |
∂2u |
, |
|
|
|
|
|
|
|
|
|
|
||||||
∂t2 |
|
|
∂ξ2 |
|
∂ξ∂η |
|
∂η2 |
|||||||
|
∂t |
∂t |
|
|
|
|
|
|
|
|||||
и подставив полученные выражения в уравнение (1). Уравнение
∂2u = 0 ∂ξ∂η
интегрируется весьма просто. Записав его в виде
∂ ∂u = 0 , ∂η ∂ξ
будем иметь ∂∂ξu , где ω(ξ) — произвольная функция.
Интегрируя полученное уравнение по ξ (η рассматривается как параметр), найдем, что
u = ∫ ω(ξ)dξ +θ2 (η),
где θ2 (η) — произвольная функция аргумента η . Полагая ∫ ω(ξ)dξ =θ1(ξ), получим
u =θ1(ξ)+θ2 (η).
Возвращаясь к исходным переменным x,t , получим
u(x,t)=θ1(x − at)+θ2 (x + at). |
(3) |
Непосредственной проверкой убеждаемся, что функция u(x,t), |
|
определяемая формулой (3), где θ1 и θ2 — |
произвольные |
дважды непрерывно дифференцируемые функции своих аргументов, есть решение уравнения (1). Это общее решение (решение Даламбера) волнового уравнения (1): всякое решение уравнения (1) может быть представлено в виде (3) при соответствующем выборе функций θ1 и θ2 . В частности,
каждое слагаемое в формуле (3) также является решением уравнения (1).
Физический смысл решения
22
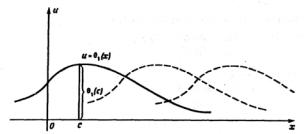
u =θ1(x − at) |
(4) |
таков. При t = 0 имеем u =θ1(x) (рис. |
1). Если наблюдатель, |
выйдя в начальный момент t = 0 из |
точки x = c оси Ox , |
передвигается по этой оси в положительном направлении со
скоростью a , так что для |
абсциссы |
его положение |
имеем |
|
dx = a , откуда x = at + c |
и x − at = c , то |
для |
него |
|
dt |
|
|
|
|
u =θ1(x − at)=θ1(c)= const . |
Иными |
словами, |
для |
такого |
наблюдателя смещение и струны, определяемое формулой (4), будет все время постоянным и равным θ1(c).
Рис. 1 Тем самым, решение (4) представляет прямую волну,
которая распространяется в положительном направлении оси Ox со скоростью a . Если за θ1(ξ) взять sinξ , то будем иметь
синусоидальную волну. Решение
u =θ2 (x + at)
представляет обратную волну, которая распространяется со скоростью a в отрицательном направлении оси Ox .
Таким образом, решение (3) является суммой прямой и обратной волн.
Это приводит к следующему графическому способу построения формы струны в любой момент времени t: сначала строим кривые u =θ1(x) и u =θ2 (x), изображающие прямую и
обратную волны в начальный момент времени t = 0 , а затем, 23
не изменяя их формы, передвигаем их одновременно на величину at > 0 в разные стороны, кривую u =θ1(x) — вправо,
u =θ2 (x) — влево. Чтобы получить график струны, достаточно
построить алгебраическую сумму ординат передвинутых кривых.
1.2. Решение задачи Коши для неограниченной струны
Задача Коши для неограниченной струны состоит в следующем: найти функцию u(x,t) C2 , удовлетворяющую уравнению
|
∂2u |
= a2 ∂2u |
, t > 0 , − ∞ < x < +∞ |
|
||||
|
∂t2 |
|
∂x2 |
|
|
|||
и начальным условиям |
|
|
|
|
|
|
||
u | |
=ϕ |
(x), |
|
∂u |
|
|
=ϕ (x), − ∞ < x < +∞, |
(5) |
|
|
|||||||
t =0 |
0 |
|
|
∂t |
|
|
1 |
|
|
|
|
|
|
t =0 |
|
||
где ϕ0 (x) C2 (R1 ), ϕ1(x) C1(R1 ). В начальный момент |
t = 0 |
|||||||
функция ϕ0 (x) определяет форму струны, а функция ϕ1(x) |
||||||||
задает распределение скоростей ∂u вдоль струны. |
|
|||||||
|
|
|
|
|
|
|
∂t |
|
Допустим, что решение рассматриваемой задачи |
||||||||
существует; тогда оно дается формулой |
|
|||||||
|
u(x,t)=θ1(x − at)+θ2 (x + at). |
(3) |
||||||
Определим функции θ1 и θ2 таким образом, чтобы |
||||||||
удовлетворялись начальные условия (5). Имеем |
|
|||||||
|
u(x,o) |
=θ1(x)+θ2 (x)=ϕ0 (x), |
(6) |
|||||
|
ut (x,0)= −a[θ1′(x)−θ2′(x)]=ϕ1(x). |
(7) |
||||||
Интегрируя второе равенство, получим |
|
|||||||
|
θ (x)−θ |
2 |
(x) |
= − 1 xϕ (α)dα + C , |
|
|||
|
1 |
|
|
|
|
1 |
|
|
a ∫0
где С — произвольная постоянная. Из равенств
24

θ (x)+θ (x)=ϕ (x), θ (x)−θ (x)= − |
1 |
|
xϕ (α)dα + C |
|
|||||||||||||||||||||||
1 |
2 |
|
|
|
0 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
a |
∫0 |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
находим |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||
|
|
|
θ1(x)= |
2 |
ϕ0 |
(x)− |
|
|
|
∫0ϕ1(α)dα |
+ |
2 |
, |
|
|||||||||||||
|
|
2a |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
|
C |
|
|||
|
|
|
θ2 (x)= |
2 |
ϕ0 |
(x)− |
|
|
∫0 |
ϕ1(α)dα |
− |
2 . |
|
||||||||||||||
|
|
2a |
|
||||||||||||||||||||||||
Подставляя найденные выражения для θ1 |
и θ2 в формулу (3), |
||||||||||||||||||||||||||
получим |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x,t) |
|
ϕ0 (x − at)− |
|
|
|
x−at |
ϕ1(α)dα + |
|
|||||||||||||||||
|
|
= |
|
|
∫0 |
|
|
||||||||||||||||||||
|
|
2 |
2a |
|
|
||||||||||||||||||||||
|
|
1 |
|
(x + at) |
1 |
|
x+at |
ϕ1(α)dα, |
|
|
|
|
|||||||||||||||
|
|
+ |
|
ϕ0 |
+ |
|
|
∫0 |
|
|
|
|
|
||||||||||||||
или |
|
2 |
2a |
|
|
|
|
|
|||||||||||||||||||
u(x,t)= ϕ0 (x − at)+ϕ0 (x + at) + |
1 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
x+atϕ (α)dα |
(8) |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2a ∫x−at |
1 |
|
|||||
— формулу Даламбера. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ0 (x) C2 (R1 ), |
|||||||||
Нетрудно |
|
проверить, |
что |
|
|
|
если |
|
|||||||||||||||||||
ϕ1(x) C1(R1 ), |
то функция |
u = (x,t), |
|
определяемая формулой |
|||||||||||||||||||||||
(8), удовлетворяет уравнению (1) и начальным условиям (5), т. е. решает поставленную задачу.
Полученное решение единственно. В самом деле, если бы существовало другое решение задачи (1), (5), то оно также представлялось бы формулой (8) и, значит, совпадало с построенным решением.
Задача. Пользуясь формулой Даламбера для решения задачи Коши
∂2u |
= a2 ∂2u , t > 0 , − ∞ < x < +∞, |
||
∂t2 |
|
∂x2 |
|
u(x,0)=ϕ(x), |
∂u(x,0) |
=ψ (x), − ∞ < x < +∞, |
|
|
|
∂t |
|
|
|
25 |
|
показать, что u x=0 = 0 в случае нечетности обеих функций
ϕ(x) и ψ (x), а в случае их четности |
∂u |
|
|
|
= 0 . |
||
|
∂t |
|
x=0 |
|
|
||
1.3. Область зависимости
Из формулы Даламбера (8) видно, что значение решения u(x,t) в точке Р с координатами (x,t) зависит только от
значений функций ϕ0 и ϕ1 в точках отрезка γP = [x − at, x + at] оси Ox .
Отрезок γP оси Ox называют областью зависимости для точки Р (рис. 2).
Фактически значения ϕ0 входят в решение только в концах этого отрезка, в то время, как значения ϕ1 берутся на всем отрезке γP .
Говорят также, что решение u(P) «не замечает» данных задачи вне γP .
Рис.2
2. Исследование формулы Даламбера
Рассмотрим два частных случая, которые дают представление о поведении решения уравнения
∂2u |
= a |
2 |
∂2u |
(1) |
∂t2 |
|
∂x2 |
||
|
|
|
||
|
26 |
|
|
|
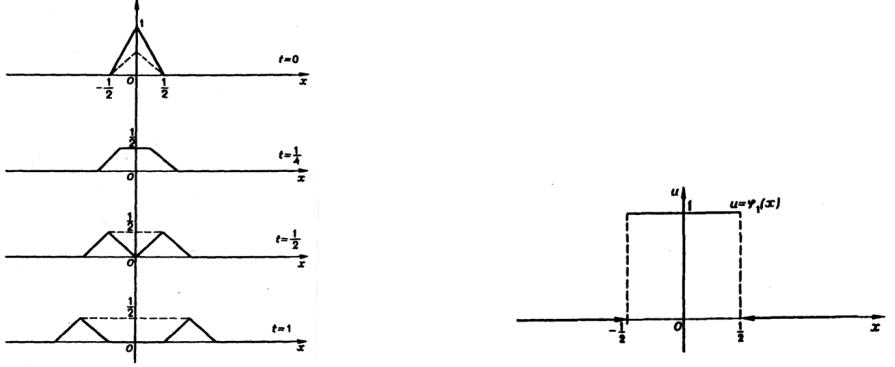
Случай 1. Пусть ϕ1(x)≡ 0 , а график функции ϕ0 (x) имеет
вид, изображенный на рис. 3 а. Будем считать для простоты, что a =1. Тогда формула Даламбера примет вид
u(x,t)= ϕ0 (x − at)+ϕ0 (x + at) . 2
Чтобы получить график решения u(x,t) рассматриваемого
как функция от х при каком-нибудь фиксированном положительном t, поступаем так: сначала начертим два одинаковых совпадающих графика, которые получаются из графика ϕ0 (x)
уменьшением вдвое каждой ординаты (пунктир на верхнем рисунке).
a)
б)
в)
г)
Рис.3 27
Потом один из этих графиков передвинем, как целое, на t вправо по направлению положительной полуоси Ox , а другой
— на t влево. После этого построим новый график, у которого ордината при каждом значении х равна сумме ординат двух передвинутых графиков. На рис. 3 б, 3 в и 3 г этим способом
|
1 |
|
1 |
|
|
построены графики u x, |
4 |
|
, u x, |
2 |
, u(x,1) соответственно. |
|
|
|
|
||
Мы видим, что при выбранных начальных условиях в каждой точке струны после прохождения обеих волн (для точек, лежащих вне области начального смещения, — после
прохождения только одной) наступает покой. |
||||||||||
Случай 2. Пусть ϕ0 (x)≡ 0 , а |
|
|
|
|
|
|
|
|
|
|
|
|
при |
|
x |
|
|
≤ |
1 |
, |
|
|
|
|
|
|||||||
|
1 |
|
|
|
2 |
|||||
ϕ1 |
(x)= |
|
|
|
|
|
|
|
|
|
|
0 |
при |
|
|
x |
|
> 1 |
|||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
(рис.4).
В этом случае говорят, что струна имеет только начальный импульс. Решение (8) принимает вид (для простоты считаем a =1):
Рис.4
28
|
u(x,t)= |
1 |
∫xx−+ttϕ1(α)dα. |
|
|
||||
|
2 |
u = (x,t) |
|
||||||
Для каждого фиксированного х решение |
будет |
||||||||
равно нулю до тех пор, |
|
пока пересечение интервала |
|||||||
(x −t, x + t) |
|
− |
1 |
, |
1 |
|
, пусто; |
u(x,t) |
|
с интервалом |
2 |
2 |
, где ϕ1(t)≠ 0 |
||||||
|
|
|
|
|
|
|
|||
будет изменяться в течение того промежутка времени, пока
увеличивающийся интервал |
(x −t, x + t) будет накрывать все |
|||||||||||
|
|
1 |
1 |
|
|
|
|
|
||||
большую часть интервала − |
2 |
, 2 |
. После того, как интервал |
|||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
(x −t, x + t) заключит внутрь себя интервал |
− |
2 , |
2 |
величина |
||||||||
u(x,t) будет оставаться неизменной и равной |
|
|
|
|
||||||||
1 |
|
|
1 |
|
ϕ (α)dα. |
|
|
|
(9) |
|||
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
1 |
1 |
|
|
|
|
|
|||
|
2 ∫− |
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|||||
Чтобы получить график, представляющий форму струны при различных t, поступаем следующим образом. Обозначим через Ф(z) какую-нибудь первообразную функцию для ϕ1(z).
Тогда
u(x,t)= 12 [Ф(x + t)−Ф(x −t)].
29
a)
б)
в)
г)
Рис.5
Для построения графика u(x,t) вычерчиваем графики функций 12 Ф(x) и − 12 Ф(x), а затем каждый из этих графиков
передвигаем, как целое, на расстояние t вдоль оси Ох, первый график влево, а второй — вправо. Сложив ординаты передвинутых графиков, получим график функции u(x,t)
(рис. 5).
По истечении достаточно большого промежутка времени
30
каждая точка струны переместится и получит стационарное отклонение uст , определяемое интегралом (9). В этом случае
мы имеем, следовательно, остаточную деформацию (гистерезис).
3. Корректность постановки задачи Пример Адамара некорректно поставленной задачи
В связи с изучением физически детерминированных явлений вводится понятие корректности задачи.
Определение. Говорят, что математическая задача поставлена корректно, если
1)решение задачи существует в каком-то классе M1 функций;
2)решение задачи единственно в некотором классе M2
функций; 3) решение задачи непрерывно зависит от данных задачи
(начальных и граничных условий, коэффициентов уравнения и т. д.).
Множеством M1 ∩ M2 функций называется классом
корректности рассматриваемой математической задачи.
В теории обыкновенных дифференциальных уравнений доказывается, что задача Коши
∂∂yx = f (x, y), y(x0 )= y0
поставлена корректно, если функция f (x, y) непрерывна по совокупности аргументов и имеет ограниченную производную
∂∂fy в некоторой области, содержащей точку (x0 , y0 ).
Рассмотрим задачу Коши для неограниченной струны
∂2u |
= a |
2 |
∂2u |
, t > 0 |
, − ∞ < x < +∞, |
(1) |
∂t2 |
|
∂x2 |
||||
|
|
|
|
|
||
|
|
|
31 |
|
|
|
u | |
=ϕ |
(x), ∂u |
|
=ϕ (x), − ∞ < x < +∞, |
(2) |
|
|||||
t =0 |
0 |
∂t |
|
1 |
|
|
|
|
t =0 |
|
|
ϕ0 (x) C2 (R1 ), ϕ1(x) C1(R1 ). |
|
||||
Выше мы установили, что решение задачи (1)-(2)
1)существует и
2)единственно.
Покажем, что при непрерывном изменении начальных условий это решение изменяется непрерывно.
Теорема 1. Каков бы ни был отрезок [0,t0 ] изменения
времени t и |
каково бы |
|
ни было ε > 0 , найдется |
такое |
||||||||||||
δ = δ(ε,t0 )> 0 , |
что для любых двух решений u(x,t) и |
~ |
(x,t) |
|||||||||||||
u |
||||||||||||||||
уравнения (1), отвечающих начальным условиям |
|
|
||||||||||||||
|
|
u(x,0)=ϕ |
0 |
(x), |
∂u(x,0) |
=ϕ (x), |
|
|
||||||||
|
|
|
|
|
|
|
|
|
∂t |
1 |
|
|
||||
|
|
~ |
|
|
|
|
~ |
|
~ |
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
∂u (x,0) |
|
|
|||||||
|
|
u (x,0)=ϕ(x), |
∂t |
=ϕ1(x), |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
для 0 ≤ t ≤ t0 , − ∞ < x < +∞, выполняется неравенство |
|
|
||||||||||||||
|
|
|
|
|
|
~ |
|
|
|
|
|
|
< ε , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
u (x,t)−u(x,t) |
|
|
|
|
||||||
если только |
~ |
|
|
|
|
|
|
|
~ |
|
< δ , − ∞ < x < +∞ |
|
|
|||
|
|
|
< δ , |
|
|
|
|
|
(3) |
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
ϕ0 (x)−ϕ0 (x) |
|
ϕ1(x)−ϕ1(x) |
|
|
|||||||||||
(малое изменение начальных условий влечет за собой малое изменение решений).
Функции u(x,t) и u~(x,t) связаны со своими начальными
условиями формулой Даламбера, так что |
|
|
|
|
||||||||
~ |
|
|
|
~ |
(x − at) |
−ϕ0 (x − at) |
|
|
|
|
||
(x,t)−u(x,t) |
= |
ϕ0 |
+ |
|
|
|||||||
u |
|
|
2 |
|
|
|
|
|||||
|
|
~ |
|
|
~ |
|
1 |
|
x+at ~ |
|
|
|
|
|
ϕ0 (x + at)−ϕ0 |
(x + at) |
|
|
|
|
|||||
|
+ |
|
|
|
2 |
|
+ |
|
|
(ϕ1 |
(α)−ϕ1 |
(α))dα , |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2a ∫x−at |
|
|
|||
откуда
32
