
2875
.pdf
Рие. IV.15. Поверхность, задаваемая функцией Розенброка
Рис. IV.16. Карта линий уровня функции Розенброка
Листинг IV.22. Файл R_y.m function z=R_y(x,y) N=length(x);
Z=zeros(N); for i=l:N
for j=l:N z(I,j)=200*(y(j)-x(i).^2);
end;
end;
7.Создайте файл R_xx.m (листинг IV.23), содержащий описа- ние функции, возвращающей значение второй производной по переменной х.
Листинг IV.23. Файл R_xx.m function z=R_xx(x,y) N=length(x);
Z=zeros(N); for i=l:N for j=l:N
z(i,j)=1200*x(i).^2-400*y(j)+2; end;
end;
8.Создайте файл R_yy.m (листинг IV.24), содержащий описа- ние функции, возвращающей значение второй производной по переменной у.
Листинг IV.24. Файл R_yy.m function z=R_yy(x,y) N=length(x);
z=zeros (N); for i=l:N
for j=l:N z(i,j)=200;
end;
end;
9. Создайте файл R_xy.m (листинг IV.25), содержащий описа- |
B(2,l)=R_y(x,y); |
ние функции, возвращающей значение смешанной производной |
z=A^-l*B; |
по переменным х, у. |
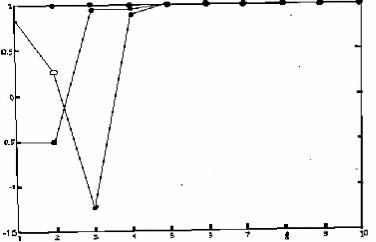
12.Визуализируйте итерационный процесс (рис. IV.17-IV.19). |
Листинг IV.25. Файл R_xy.m |
» plot(x,'-x'); |
function z=R_xy(x,y) |
» hold on |
N=length(x); |
» plot(у,'-о'); |
z=zeros(N); |
» hold off |
for i=l:N |
» plot(z,'-o') |
for j=l:N |
» plot3(x,y,z,'-o'); grid on |
z(i,j)=-400*x(i); |
|
end; |
|
end; |
|
10. Создайте файл Rg.m (листинг IV.26), содержащий описание |
|
функции, возвращающей значения обратной матрицы вторых |
|
производных на вектор-градиент. |
|
Листинг IV.26. Файл Rg.m |
|
function z=Rg(x,y) |
|
A(l,l)=R_xx(x,y); |
|
A(l,2)=R_xy(x,y); |
|
A(2,l)=R_xy(x,y); |
|
A(2,2)=R_yy(x,y); |
|
B(l,l)=R_x(x,y); |
|
B(2,l)=R_y(x,y); |
|
z=А^-1*В; |
Рис. IV.17. Зависимость значений координат решения уравне- |
11.Создайте файл RnO.m (листинг IV.27), содержащий описа- |
ния от номера итерации |
ние функции, возвращающей значения переменных и соответ- |
|
ствующих значений функции Розенброка. |
|
Листинг IV.27. Файл RnO.m |
|
function z=Rg(x,y) |
|
A(l,l)=R_xx(x,y); |
|
A(l,2)=R_xy(x,y); |
|
A(2,l)=R_xy(x,y); |
|
A(2,2)=R_yy(x,y); |
|
B(l,l)=R_x(x,y); |
|
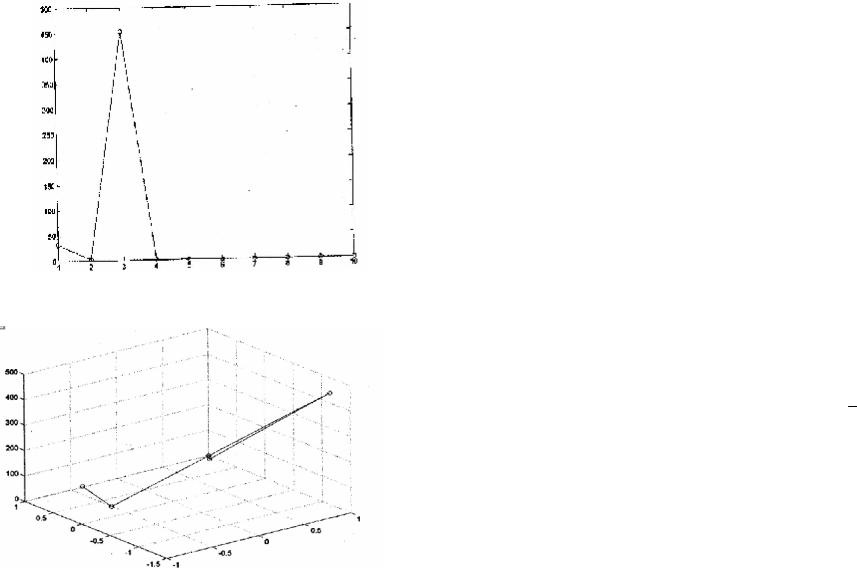
Рис. IV.18. Зависимость значения исследуемой функции от но-
мера итерации
Рис. IV.19. Траектория итерационного процесса в пространстве
4.5. Решение систем нелинейных уравнений средствами пакета MATLAB
Средствами пакета MATLAB найдем решение системы не-
линейных уравнений
ìïx2 + y2 - 4 = 0
í
ïy - x2 -1 = 0
î
которая может быть записана в векторном виде
|
|
|
|
(x) = 0, |
|
|
|||
F |
|
|
|||||||
где |
|
|
|
|
|
||||
|
|
æ |
2 |
+ x |
2 |
- 4 |
ö |
||
|
|
|
ç x1 |
2 |
÷ |
||||
F (x) = ç x |
2 |
- x |
2 |
-1 |
÷, |
||||
è |
1 |
|
ø |
||||||
æ x ö
x= ç 1 ÷. çè x2 ÷ø
Для этого необходимо выполнить следующую последова- тельность действий:
1. Создать файл fm.m (листинг IV.28), содержащий описание функции, возвращающей значения функции F (x).
Листинг IV.28. Файл fm.m function z=fm(x) z(l,l)=x(l).^2+х(2)^2-4; z(2,l)=x(2)-x(l)^2-l;
2. Задать вектор начального приближения.
»z(1,1)=1;
»z(2,1)=1;
3.Обратиться к встроенной функции fsolve(), возвращающей решение системы линейных уравнений.
» х = fsolve ( 'fm' ,z,optimset( 'f solve' ) ) Optimization terminated successfully:

Relative function value changing by less than OPTIONS . TolFun
%Процесс оптимизации завершен
%Относительная величина изменения функции меньше чем
%переменная OPTIONS . TolFun
х = 0.8895 1.7913
4.Проверить полученное решение.
»fm(x) ans =
l.0e-008 * 0.5162 -0.4888
Для одновременного вывода координат вектора решения уравнения и соответствующего значения вектор-функции сле- дует выполнить команду:
»[х fval] = f solve ( 'fm' ,z,optimset('f solve'))
Optimization terminated successfully:
Relative function value changing by less than OPTIONS . TolFun x =
0.8895
1.7913
fval = l.0e-008 * 0.5162 -0.4888
Для вывода на экран монитора значений вектора-решения и соответствующего значения функции F (x) следует выполнить
команду:
» [х fval exitflag] = fsolve('fm',z,optimset('Display','Iter'));
|
|
Norm of |
|
First-order |
|
|
Iteration |
Func-count f(x) step |
optimality |
CG-iterations |
|||
1 |
4 |
5 |
1 |
|
5 |
0 |
2 |
7 |
1 |
1 |
|
4 |
1 |
3 |
10 |
0.0026 |
0.223607 |
0.17 |
1 |
|
4 |
13 |
4.53078e-008 |
0.013546 |
0.00055 |
1 |
|
5 |
16 |
5.05378e-017 |
7.18274e-005 1.79e-008 |
1 |
||
Optimization terminated successfully:
Relative function value changing by less than OPTIONS.TolFun
В ряде случаев более удобным оказывается метод Ньюто- на, при использовании которого (как описано в разделе 4.2) необходимо знать в данной точке и значения функции, и зна- чения якобиана, что позволяет реализовать итерационный про- цесс. Метод Ньютона в пакете MATLAB реализуется сле- дующей последовательностью действий:
1. Создайте файл Fml.m (листинг IV.29), содержащий описание функции, возвращающей одновременно значения функции
F (x)и значения якобиана.
Листинг IV.29. Файл Fml.m function [z,J]=fm(x) z(l,l)=x(l).^2+х(2)^2-4; z(2,l)=x(2)-x(l)^2-l; J(l,l)=2*x(l);
J(l,2)=2*x(2);
J(2,l)=-2*x(l); J(2,2)=l;
2.Включите режим использования метода Ньютона и отобра- жения итерационного процесса на экране.
» options=optimset('Jacobian','on','Display','Iter');
3.Обратитесь к встроенной функции fsolve(), возвращающей
решение системы линейных уравнений. |
|
|
|
|||||
» [х fval exitflag] = fsolve('fml',z,options); |
|
|
|
|||||
|
|
Normof First-order |
|
|
|
|
||
Iteration |
Func-count |
f(x) |
step |
optimality |
CG-iterations |
|||
1 |
2 |
|
5 |
1 |
|
5 |
|
0 |
2 |
3 |
|
1 |
1 |
|
4 |
|
1 |
3 |
4 |
|
0.0026 |
0.223607 |
|
0.17 |
|
1 |
4 |
5 |
4.53076e-008 |
0.013546 |
|
0.00055 |
1 |
||
5 |
6 |
5.04984e-017 |
7.18272e-005 |
1.79e-008 |
1 |
|||
Optimization terminated successfully:
Relative function value changing by less than OPTIONS.TolFun
Рассмотрим реализацию метода спуска средствами пакета MATLAB на примере системы нелинейных уравнений, который был разобран ранее в настоящем разделе. Напомним, что для этого (следуя подходу, описанному в разделе 4.3) нужно из уравнений исходной системы создать новую положительно оп- ределенную функцию, минимум которой и будет искомым ре- шением системы нелинейных уравнений. Следовательно, для
нахождения решения рассматриваемой системы нелинейных уравнений необходимо выполнить следующую последователь- ность действий:
1. Создать файл F_sq.m (листинг IV.29), содержащий описание функции, возвращающей значения суммы квадратов функций f(x, у) = х2 + у2 -4 и g(x,y)=y-x2-1.
Листинг IV.30. Файл F_sq.m function z=F_sq(x)
s=fm(x); z=s(1,1).^2+s(2,1).^2;
Здесь мы предполагаем, что ранее файл fm.m, содержащий описание функции, возвращающей значения функций f (x,y) и g(х, у), уже создан.
2.Задать начальное приближение, в окрестности которого бу- дет находиться минимум функции f(х, у)2 + g(x, у)2 .
» x=[1;1];
3.Обратиться к встроенной функции fminsearch ()
» fminsearch ('f_sq',х) ans =
0.8896
1.7913
Способы обращения к функции fminsearch( ) и список ее
формальных параметров аналогичны способам обращения к функции fsolve () и списку ее формальных параметров.

V.Интерполированиефункций
Вданном рассмотрим основные методы решения задачи об интерполяции функции, заданной таблично (интерполяционный полином, полином Лагранжа, полином Ньютона, сплайн-интерполяция) и опишем соответствующие алгоритмы и их программные реализации, а также обсудим использование соответствующих функций пакета MATLAB.
5.1. Постановка задачи
Пусть известные значения некоторой функции f(х) образуют следующую таблицу:
Таблица V.1 Исходные данные в задаче интерполяции
X |
Хо |
Х 1 |
. . . |
Хп |
f(x) |
Уо |
У1 |
. . . |
Уп |
|
|
|
|
|
Требуется получить значение функции f(x) для значения аргумента xє [ x0, xn ], несовпадающего ни с одним из значений хi (i = 0, 1, ..., n).
Решение задачи сводится к поиску некоторой приближающей функции F(х), близкой в определенном смысле к функции f(x), для которой известно аналитическое выражение.
Классический подход к решению задачи построения приближающей функции основан на требовании строгого совпадения значений функций f(x) и F(x) в точках x,(i = 0, 1,...,n)
F(x0) = y0,F(x1) = y1 ,..., F(xn) = yn. |
(V.1) |
В данном случае нахождение приближенной функции называется интерполированием, а точки х0, x1 ,..., хn называются узлами интерполяции.
Будем искать интерполирующую функцию F(x) |
в виде |
||
многочлена степени n: |
|
|
|
|
n |
n−k |
|
Pn (x) = a0xn + a1xn -1 |
+ … an -1x + an = åak n |
|
(V.2) |
k =0
Условия (V.1), наложенные на многочлен, позволяют однозначно определить его коэффициенты. Действительно, требуя для Рn(х) выполнения условий (V.1), получаем линейную систему, состоящую из (n + 1) уравнения:
n |
|
åak xi n−k yi , i = 0, 1, K , n. |
(V.3) |
k =0
Решив систему (V.3) относительно неизвестных а0, а1, … , аn , находим значения этих неизвестных и, подставив в (V.2), находим аналитическое выражение аппроксимирующей функции.
Система (V.4) всегда имеет единственное решение, т. к. ее определитель
x0n |
x0n−1 |
K |
1 |
|
|
|
|
||||
x1n |
x1n−1 |
K |
1 |
, |
(V.4) |
M |
M |
K |
M |
||
xnn |
xnn−1 |
K |
1 |
|
|
|
|
|
|
известный в алгебре как определитель Вандермонда, отличен от нуля. Следовательно, интерполяционный многочлен Рn(х) существует и единственен.
Пример V.1. Решить, используя пакет MATLAB, задачу интерполяции с помощью полинома n-ой степени для функции f (х) = sin (x), заданной таблично в восьми точках на интервале [0, 2π].
1.Задайте табличные значения интерполируемой функции.
»N = 8;
»1=1: N;
»x(i)=2*pi/(N-l)*(i-l);
»y=sin(x);
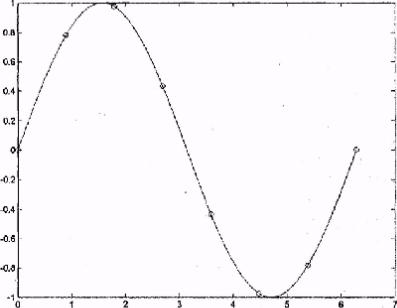
2. Визуализируйте табличную зависимость и истинные значения функции (рис. V.1).
Рис. V.1. График функции f (x) = sin (x) и табличных значений, используемых для решения задачи интерполяции
»М=1000;
»j=l:M;
»X(j)=2*pi/(M-l)*(j-1);
»Y=sin(X) ,
»plot(x,y, ' о');
»hold on
»plot (x,y)
3. Создайте файл Pol.m (листингV.1), содержащий описание функции, возвращающей значения полинома (V.2).
Листинг V.1. Файл Pol. M function z=Pol (x,a)
N = length(a); M= length(x); for j=l:M s=0;
for i=l:N
s= s+a(i)*x(j).^(N-i); end;
z(j)=s;
end;
4. Создайте файл Vandermortd.m (листинг V.2), содержащий описание функции, возвращающей значения элементов матрицы Вандермонда.
Листинг V.2. Файл Vandermond. m function z = Vandermond (x)
N = length(x);
z = ones (N,N) ; for i = 1:N
z(i,j) = x(i). ^(N-j); end;
end;
5.Вычислите значения элементов матрицы Вандермонда. » M=Vandennond(x) ;
6.Вычислите значения коэффициентов полинома.
» а = М^ - 1*у'; 7. Вычислите значения полинома в заданных
промежуточных точках
» Y1=Pol (X,a);
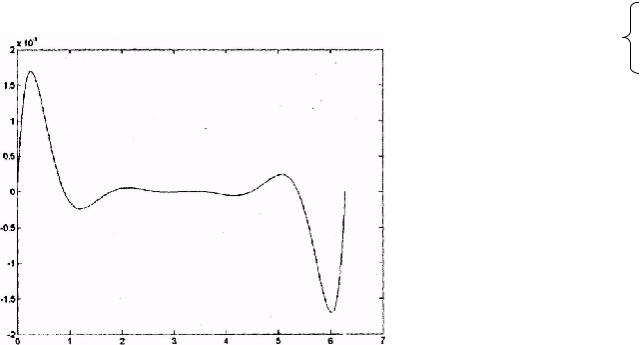
8. Постройте разность между точными и интерполированными значениями функции (рис. V.2).
Рис. V.2. Погрешность аппроксимации функции f (x) = sin (x) полиномом 8-й степени.
5.2. Интерполяционный полином Лагранжа
Для функции, заданной табл. V.1, построим интерполяционный многочлен Ln(x), степень которого не выше п и выполнены условия (V.1).
Будем искать Ln (x) в виде
Ln(x) = lo(x) + l1(x) + … + ln (x) , |
(V.5) |
|
где li – многочлен степени n, причем |
|
|
li (xk) = |
yi , если i = к |
|
. |
(V.6) |
|
0, если i ≠ к
Очевидно, что требование (V.6) с учетом (V.5) обеспечивают выполнение условий (V.1).
Многочлены li ,(x) составим следующим образом:
li (x)=ci (x –x0)(x - xi) · …· (x – xi-1)(x – xi+1)· …·(x - xn), (V.7)
где сi— постоянный коэффициент, значение которого находится из первой части условия (V.6):
сi |
= |
|
|
|
yi |
|
|
|
|
|
, |
(V.8) |
||
(xi |
- x0 ) × K ×(xi |
- xi−1)(xi - xi+1) × K × (xi - xn ) |
||||||||||||
|
|
|
|
|
||||||||||
Подставив с, в (V.7) и далее в (V.5), окончательно получим: |
||||||||||||||
|
|
|
n |
(x - x0 ) × K × (x - xi−1) × (x - xi +1) × K × (x - xn ) |
||||||||||
Ln (x) = å yi |
|
|
|
|
|
|
. (V.9) |
|||||||
(x - x ) × K ×(x - x |
− |
)(x - x |
+ |
|
) × K × (x - x ) |
|||||||||
|
|
|
i =0 |
i 0 |
|
i i |
1 |
|
i |
n |
||||
|
|
|
i i 1 |
|
|
|||||||||
Формула (V.9) решает поставленную задачу.
Пример V.2. Решить, используя пакет MATLAB, задачу интерполяции с помощью многочлена Лагранжа для функции f(x) = sin(x), заданной таблично в восьми точках на интервале [0, 2π].
1. Задайте табличные значения интерполируемой функции.
»N=8;
»i = 1:N;
»x(i)= 2*pi/(N-1)*(i-1);
»y=sin(x);
2. Создайте файл Lagrange.m (листинг V.3), содержащий описание функции возвращающей значение многочлена
li ,(x).
function z=Lagrange (x, i , X, Y)
%x - абсцисса точки интерполяции
%I - номер полинома Лагранжа
%X - вектор, содержащий абсциссы узлов интерполяции
%Y - вектор, содержащий ординаты точек интерполяции
N=length(X);
L=l;
for j=l:N
if not(j==i)
L=L*(x-X(j)) / (X(i)-X(j)); end;
end; z=L*Y(i);
3. Создайте файл Pol_Lagr.m (листинг V.4), содержащий описание функции, возвращающей значения полинома Лагранжа.
Листинг V.4 . Файл Lagr. m function z=Pol_I<agr(x,X,Y)
%x - абсцисса точки интерполяции
%i - номер полинома Лагранжа
%X - вектор, содержащий абсциссы узлов интерполяции
%Y - вектор, содержащий ординаты точек интерполяции
N=length(X); s=0,-
for i=l:N
s=s+Lagrange (x , i , X, Y ); end;
z=s;
4.Задайте число промежуточных точек, вычислите их координаты и точные значения интерполируемой функции.
» М=1000; » j=1:M;
» X(j) =2*pi / (M-1) * (j -1); » Y = sin (X)
5.Вычислите значения полинома Лагранжа в промежуточных точках.
» for j=l:M
Y2 ( j) =Pol_Lagr (X ( j) , x, у) ; end;
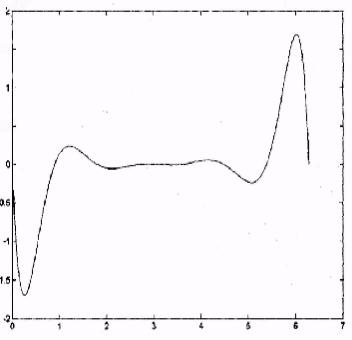
6.Постройте разность между точными и интерполированными значениями функции (рис. V.3).
Рис. V.3. Погрешность аппроксимации функции f (х) = sin (х) полиномом Лагранжа
5.3. Интерполяционный полином Ньютона для равноотстоящих узлов
Интерполяционные формулы Ньютона строятся для функций, заданных таблицами с равноотстоящими значениями аргумента h:
h = xi +1 – xi (i =1, 2, … , n ) |
(V.10) |
5.3.1 . Конечныеразности
Для функции, заданной табл. V.1 с постоянным шагом (V.10), определим разности между значениями функции в соседних узлах интерполяции:
yi = yi +1 – yi . (V.11)
Такое выражение называют конечными разностями первого порядка. Из конечных разностей первого порядка можно образовать конечные разности второго порядка:
2yi = yi +1– yi=(yi +2–yi +1)–(yi +1–yi)=yi +2– 2yi +1+yi. (V.12)
Аналогично получают выражение для конечных разностей третьего порядка:
3yi = 2yi +1 – 2yi = (yi +3 – 2yi +2 + yi +1) – (yi +2 – 2yi +1 + yi) =
|
|
|
= yi +3 – 3yi +2 + 3yi +1 – yi . |
(V.13) |
|
Методом математической индукции можно доказать, что |
|||||
Dk yi = yi+k |
- kyi+k −1 |
+ |
k(k -1) |
yi +k −2 -K + (-1)k yi . |
(V.14) |
|
|||||
|
|
2! |
|
|
|
5.3.2. Первая интерполяционная формула Ньютона
Будем искать интерполяционный полином в виде:
Pn (x) = a0 |
+ a1(x - x0 ) + a2 |
(x - x0 )(x - x1) +K+ |
(V.15) |
|
+K+ an (x - x0 ) ×K× (x - xn−1) |
||||
|
||||
Значения коэффициентов a0, a1, … , an найдем из условия совпадения значений исходной функции и многочлена в узлах. Полагая х = х0 , из (V.15) найдем у0 = P0(x0) = a0 , откуда а0 = у0. Далее, последовательно придавая х значения x1, и х2, получаем:
|
yi = Pn (x1 ) = a0 + a1 (x1 - x0 ) = a0 + a1h, |
|
|
|
|||||||||||||||
откуда |
|
|
|
|
|
|
a |
= |
Dy0 |
|
, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y2 = Pn (x2 ) = a0 + a1 (x2 - x0 ) + a2 (x2 - x0 )(x2 - x1 ) = |
|
||||||||||||||||||
|
|
= a |
0 |
+ a 2h + a |
2 |
2h2 . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. |
|
|
|
|
2h2 = y |
|
|
|
|
|
|
|
|
|
|
||||
|
|
a |
2 |
2 |
- a 2h - a |
0 |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
или 2ha |
= y |
-2Dy - y |
0 |
= y -2(y - y )- y |
= y |
-2y + y |
0 |
=D2 y |
, |
||||||||||
2 |
2 |
0 |
|
|
|
|
2 |
|
|
1 |
0 |
0 |
2 |
1 |
0 |
||||
откуда |
|
|
|
|
|
|
|
a2 |
= |
D2 y0 . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2!h2 |
|
|
|
|
|
|
|
Затем, проведя аналогичные действия, можно получить
a3 = D3 y0
3!h2
В общем случае выражение для ак будет иметь вид
an = Dn y0 . (V.16) n!h2
