
2875
.pdf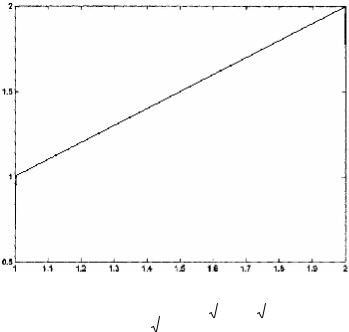
поэтому на практике используют менее строгий метод контроля точности численного решения — принцип Рунге. Данный принцип заключается в сравнении численных решений, полученных на временных сетках с шагом 2h и h, в одних и тех же узлах временной сетки. Абсолютное значение разности этих
решений характеризует величину погрешности численного решения. Недостаток настоящего подхода состоит в том, что
при данном способе контроля приходится ограничиваться квадратурными формулами, пригодными только для сеток с равномерным шагом.
Рис. X.2. Численное решение интегрального
2 |
x(s)ds |
|
|
|
|
|
|
||
уравнения x(t) = ò |
|
+ t + 1 − t + 4 + t. |
|||||||
|
|
|
|
||||||
|
t + s |
2 |
|||||||
1 |
|
|
|
|
|
|
|
|
|
Важно понимать, что необходимо согласовывать выбор конкретной квадратурной формулы (порядок ее точности) со степенью гладкости ядра интегрального уравнения. Если ядро и свободный член оказываются недостаточно гладкими, то для
вычисления интеграла не следует применять высокоточные
квадратуры, а лучше ограничится такими формулами, как формулы трапеций и прямоугольников.
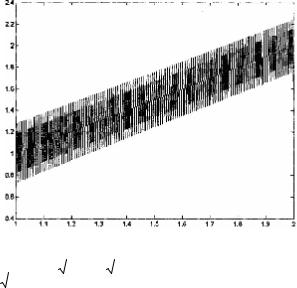
Это замечание иллюстрирует рис. X.3, на котором представлено решение уравнения из примера X.1, полученное при использовании квадратурной формулы Симпсона. Далее приведен листинг файла Solve2_g11.m (листинг X.4), содержащего описание соответствующей функции.
Листинг X.4. Файл Solve2_g11.m function [X,Y]=solve2_g11(x1,x2,N,Lambda) % задание временной сетки h=(x2-x1)/(N-1);
i=1:N; t(i)=x1+h*(i-1); s=t;
%задание коэффициентов квадратурной формулы метода Симпсона
A(1)=1/3;
A(N)=1/3;
k=0;
for i=2:N-1 if k==0
A(i)=4/3;
k=1; else
A(i)=2/3;
k=0;
end;
end;
%вычисление значений функции Q(t,s) в узлах сетки
for i=1:N for j=1:N
q(i,j)=Q11(t(i),s(j));
end;
end;
% вычисление значений функции f(t) в узлах временной сетки
F=f11(t); for i=1:N
for j=1:N if i==j
M(i,j)=1-Lambda*A(i)*q(i,j)*h; else
M(i,j)=-Lambda*A(i)*q(i,j)*h; end;
end;
end;
X=t;
Y=M^-1*F'; % нахождение решения интегрального уравнения
Для получения численного решения интегрального уравнения следует создать файлы q11.m, f11.m, Solve1_g11 и затем выполнить следующую последовательность команд:
>>x1=1; % левая граница отрезка поиска решения
>>x2=2; % правая граница отрезка поиска решения
>>Lambda=1;
>>N=300; % число узлов разбиения отрезка
>>[X,Y]=solve2_g11(x1,x2,N,Lambda);
>>plot(X,Y) % визуализация решения интегрального уравнения
%(рис. X.3)
Рис. X.3. Численное решение интегрального уравнения
2 |
x(s)ds |
|
|
|
|
|
|
||
x(t) = ò |
|
+ t + 1 − t + 4 + t. при использовании формулы |
|||||||
|
|
|
|
||||||
|
t + s |
2 |
|||||||
1 |
|
|
|
|
|
|
|
|
|
Симпсона
10.3. Квадратурный метод решения интегральных уравнений Вольтера
Так как линейные интегральные уравнения Вольтерра в отличие от уравнения Фредгольма имеют единственное непрерывное решение при любых значениях параметра λ, при нахождении
численного решения уравнения
x(t) = òt |
Q(t, s)x(s)ds + f (t), |
(X.19) |
a |
|
|
где t [а, b], можно положить λ = 1.
Учитывая, что уравнение Вольтерра формально можно считать
уравнением Фредгольма вида
x(t) = òt |
Q(t, s)x(s)ds + f (t) |
|
(X.20) |
|
a |
|
|
|
|
с ядром |
|
|
|
|
ìQ(t, s) ïðè |
a £ s £ t £ b |
, |
(X.21) |
|
K(t, s) = í |
|
|
||
î0 ïðè a £ t £ s £ b |
|
|
||
для нахождения решения рассматриваемого уравнения воспользуемся результатами предыдущего раздела.
Введем в рассмотрение временную сетку s j Î[a, b] , состоящую
из п узлов, и выберем конкретную квадратурную формулу с весами Аj, тогда приближенное решение интегрального уравнения принимает вид (X.17). Составим систему линейных алгебраических уравнений, аналогичную системе (X.18), которая в силу свойств ядра интегрального уравнения (X.21) вырождается в треугольную:
ì |
|
|
|
|
(1 - A1Q11 )x1 = f1 |
|
|
|
|
|
|
||||
ï |
|
|
- A1Q21 x1 + (1 - A2Q22 )x2 = f2 |
|
|
|
|
|
|||||||
ï |
|
|
|
|
|
|
(X.22) |
||||||||
í |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï- A Q |
n1 |
x |
1 |
- A Q |
n2 |
x |
2 |
-K + (1 - A Q |
nn |
)x |
n |
= f |
n |
. |
|
î |
1 |
|
2 |
|
n |
|
|
|
|||||||
Из (X.22) видно, что искомые значения x1, x2,…,хп находятся последовательными вычислениями по следующим формулам:
|
x1 = |
f1 |
|
, |
|
|
|
|
(X.23) |
|
|
1 − A Q |
|
|
|
|
|||||
|
|
|
1 |
11 |
|
|
|
|
|
|
|
|
|
i−1 |
|
|
|
|
|
|
|
|
|
fi + å Aj Qij x j |
|
|||||||
xi |
= |
|
j=1 |
|
|
|
|
, |
(X.24) |
|
|
1 − Ai Qii |
|
|
|||||||
|
|
|
|
|
|
|
|
|||
Пример X.2. Решение в пакете МАТLАВ интегрального |
||||||||||
уравнения |
|
|
|
|
|
|
|
|
|
|
x(t) = òt cos2 (ts3 )x(s)ds + t2 |
− |
1 |
tg(t 4 ). |
|
||||||
|
|
|||||||||
3 |
|
|
|
|
|
3 |
|
|||
(Точное решение уравнения х = t2.)
1.Создайте файл q11_2.m (листингX.5), содержащий описание функции, возвращающей значения подынтегральной функции. Листинг X.5. Файл q11_2.m
function z=Q11_2(t,s) z=t*cos(t*s.^3).^2;
2.Создайте файл F11_2.m (листинг X.6), содержащий описание функции, возвращающей значения функции f(t).
Листинг X.6. Файл F11_2.m function z=f11_2(t) z=t.^2-1/3*tan(t.^4);
3.Создайте файл Solve3_g11.m (листинг X.7), содержащий описание функции, возвращающей решение интегрального уравнения.
Листинг X.7. Файл Solve3_g11.m function [T,Y]=Solve3_g11(t1,t2,N) % задание временной сетки h=(t2-t1)/(N-1);
i=1:N; t(i)=t1+h*(i-1);
s=t;
% задание коэффициентов квадратурной формулы метода трапеций
A(1)=0.5; m=2:N-1; A(m)=1; A(N)=0.5;
%вычисление значений функции Q(t,s) в узлах сетки for i=1:N
for j=1:N Q(i,j)=Q11_2(t(i),s(j));
end;
end;
%вычисление значений функции f(t) в узлах временной сетки
F=f11_2(t);
%вычисление решения интегрального уравнения
x(1)=F(1)./(1-A(1)*Q(1,1)); for m=2:N
S=0;
for j=1:m-1 S=S+h.*A(j).*Q(m,j).*x(j);
end; x(m)=(F(m)+S)./(1-h.*A(m).*Q(m,m));
end;
T=t;
Y=x;
4. Выполните следующую последовательность команд:
>>t1=0; % левая граница отрезка поиска решения
>>t2=0.5; % правая граница отрезка поиска решения
>>N=300; % число узлов разбиения отрезка
>>[X,Y]=solve3_g11(x1,x2,N,Lambda);
>>plot(X,Y) % визуализация решения интегрального уравнения
%(рис. X.4)
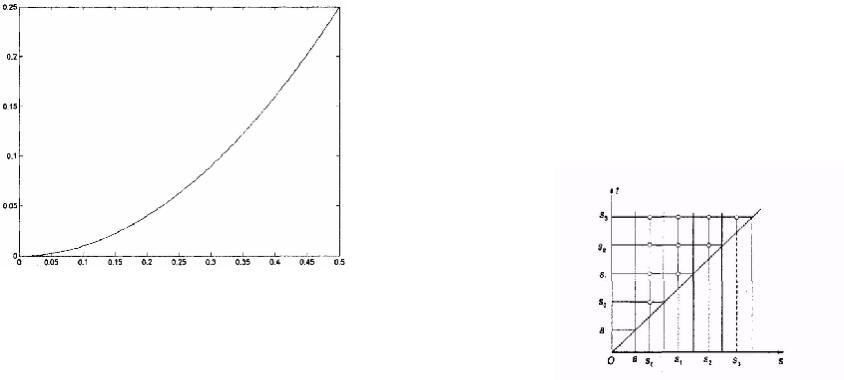
Рис. X.4. Численное решение интегрального уравнения
t |
1 |
|
|
x(t) = òt cos2 (ts3 )x(s)ds + t 2 − |
tg(t 4 ). |
||
3 |
|||
0 |
|
||
|
|
%оценка параметров решения интегрального уравнения
%методом наименьших квадратов
>>Z=[ones(size(X'))X'X'.^2];
>>a=Z\Y'
a=
-0.0000 -0.0000 1.0003
>>format long
>>a
a=
1.0е+002*
-0.00000187595514 -0.00000470664690 1.00030838604155
Получим расчетные формулы для решения уравнения Вольтерра первого рода (X.5) при использовании метода средних прямоугольников. Решения уравнения будем находить
в узлах временной сетки
t1 = a + h, t2 = t1 + h,K, ti = ti−1 + h. |
(X.25) |
Подставляя (X.25) в (X.4), получаем равенства |
|
ti |
|
òQ(TI , s)x(s)ds = f (ti ). |
(X.26) |
a
Рис. X.5. Пространственно-временная сетка, используемая для
решения уравнения Вольтерра
Из (X.26) видно, что в данном случае условие совпадения узлов квадратур si с узлами временной сетки ti не является обязательным, поэтому их можно выбрать посередине элементарных промежутков интегрирования [ti-1, ti] (рис. X.5). Выбор данной сетки означает, что
x1 ≈ x(s1 ), x2 ≈ x(s2 ),K, xn ≈ x(sn ). |
(X.27) |
Учитывая выбор квадратурной формулы и условия (X.27), запишем (X.26) в следующем виде:
hQ(t1 , s1 )x1 = f (t1 ),
hQ(t2 , s1 )x1 + hQ(t2 , s2 )x2 = f (t2 ),

hQ(t3 , s1 )x1 + hQ(t3 , s2 )x2 |
+ hQ(t3 , s3 )x3 = f (t3 ), |
(X.28) |
|||||||||||
где |
|
|
|
|
si |
= ti |
− |
h |
. |
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из равенств (X.28) последовательно находим: |
|
|
|||||||||||
|
|
x1 |
= |
|
f (t1 ) |
|
|
, |
|
|
|
(X.29) |
|
|
|
|
hQ(t1 , s1 ) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
i −1 |
|
|
|
|
|
|
|
|
|
= |
f (ti ) − håQ(ti , s j )x j |
|
|
|||||||||
xi |
|
|
|
i =1 |
|
|
|
|
|
, |
(X.30) |
||
|
|
hQ(ti , si ) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
где i = 2, 3,
Пример X.4. Найти в пакете МАТЬАВ решение интегрального
уравнения
òt |
(t2 + s2 + 1)x(s)ds = t2 − |
1 |
, |
|
|
t |
|||
1 |
|
|
|
|
используя систему узлов координатно-временной стеки, представленную на рис. X.5.
(Точное решение уравнения x(t) = t12 . )
1.Создайте файл F11_4.m (листинг X.8), содержащий описание функции, возвращающей значения функции f(t).
Листинг X.8. Файл F11_4.m function z=F11_4(t) z=t.^2-1./t;
2.Создайте файл Q11_4.m (листинг X.9), содержащий описание функции, возвращающей значения функции Q(t,s).
Листинг X.9. Файл Q11_4.m function z=Q11_4(t,s)
z=t.^2+s.^2+1;
3. Создайте файл УоИеггаП.т (листинг X.10), содержащий описание функции, возвращающей решения интегрального уравнения Вольтерра.
Листинг X.10. Файл Volterra11.m function [T,Z]=Volterra11(t1,t2,N)
%задание временной сетки h=(t2-t1)/(N-1);
i=1:N;
t(i)=t1+h*i;
s=t+h/2;
%вычисление значений ядра интегрального уравнения
%в узлах временной сетки
fоr i=1:N fоr j=1:N
q(i+1,j+1)=Q11_4(t(i),s(j)); end;
end;
%вычисление значений функции F(t) в узлах временной сетки
F(1)=F11_4(t(1)); F(i+1)=F11_4(t(1));
%Вычисление значений решения интегрального уравнения в соответствие с (X.29),(X.30)
х(1)=F(1)/(h*q(1,1)); for m=2:N
s=0;
fоr j=2:m-1 s=s+q(m,j)*m(j);
еnd;
х(m) = (F(m) -h*s)/( h*q(m,m)); end;
Т=t; Z=х;
4. Выполните следующую последовательность команд:
>>t1=1; % левая граница интервала поиска решения
>>t2=1.3;%правая граница интервала поиска решения
>>N=300; % число интервалов разбиения отрезка
%[t1,t2]
>>[Т,Z]=Voltегга11(t1,t2,N); % численного решения
% интегрального уравнения Вольтерра
>>рlоt(Т,Z); % визуализация решения уравнения
%Вольтерра (рис. X.6)
|
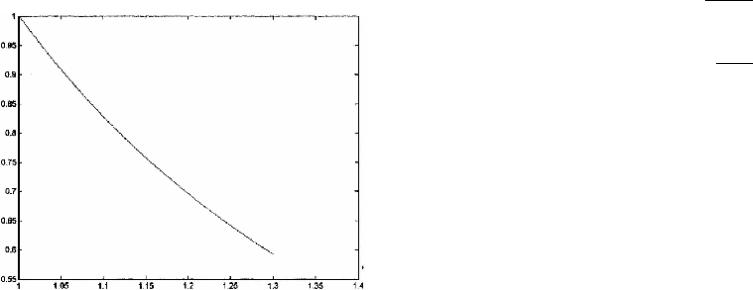
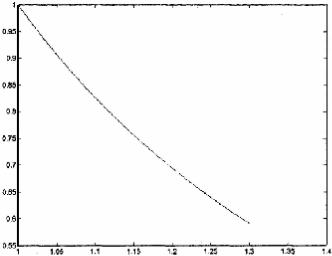
Рис. X.6. Численное решение интегрального уравнения |
||
t |
|
1 |
, полученное на пространственно-временной |
ò(t 2 |
+ s2 + 1)x(s)ds = t2 − |
||
1 |
|
t |
|
|
сетке, представленной на рис X.5. |
||
При использовании квадратурных формул замкнутого типа и совпадающей системы узлов возникает проблема вычисления значения x1=x(t1)=x(s1)=x(a), которая не возникала при решении уравнений Вольтерра второго рода. Действительно, при i=1 равенство (X.25) теряет всякий смысл.
Для нахождения начального значения x1 продифференцируем уравнение (X.5) по t.
Q(t,t)x(t) + òt |
Q¢(t, s)x(s)ds = f ¢(t). |
(X.31) |
a |
|
|
Положив в (X.31) t= а, получим |
|
|
Q(a, a)x(a) = f ′(a). |
(X.32) |
|
x(a) + f ′(a) Q(a, a)
следовательно,
x1 = fQ′(a)
11
,
. (X.33)
При использовании квадратурной формулы трапеций далее получаем:
|
|
|
h |
|
h |
|
|
|
|
|
|
|
|
f |
2 |
|
h |
|
Q |
|
|
x |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
Q21 x1 |
+ |
|
|
Q22 x2 |
= f2 |
Þ x2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||||||||
|
|
|
2 |
2 |
|
|
h |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q22 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
h |
|
h |
|
|
h |
|
|
|
|
|
|
|
|
f |
3 |
|
h |
Q |
31 |
x |
1 |
- hQ |
32 |
x |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Q31 x1 + |
|
|
Q32 x2 |
+ |
|
|
Q33 x3 |
= f3 |
Þ x3 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q33 |
|
|
|
|
||||
т. е. в общем случае при любому j= 2, 3, |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
j−1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
f j - |
Q j1 x1 - håQ jk xk |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x(s j ) » x j = |
|
2 |
|
|
|
|
|
|
k =2 |
|
|
|
|
|
. |
|
(X.34) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
h |
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
jj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример X.4. Найти в пакете МАТ1АВ решение интегрального |
|||||||||||||||||||||||||||||||||||||||
уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
òt |
(t2 + s2 + 1)x(s)ds = t2 - |
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||||||
используя замкнутые квадратурные формулы.
1. Создайте файл F11_4.m (листинг X.11), содержащий описание функции, возвращающей значения функции f(t). Листинг X.11. Файл F11_4.m
function z=F11_4(t) z=t.^2-1./t;
Откуда следует, что
2.Создайте файл dF11_4.m (листинг X.12), содержащий описание функции, возвращающей значения производной функции f(t).
Листинг X.12. Файл dF11_4.m function z=dF11_4(t) z=2*t+1/t.^2;
3.Создайте файл Q11_4.m (листинг X.13), содержащий описание функции, возвращающей значения функции Q(t,s). Листинг X.13. Файл Q11_4.m
function z=Q11_4(t)
z=t.^2+s.^2+1;
4. Создайте |
файл |
Volterra11_2.m |
(листинг X.14), |
содержащий |
описание |
функции, возвращающей решения |
|
интегрального уравнения Вольтерра на совпадающей сетке.
Листинг X.14. Файл Volterra11_2.m function [T,Z]=Volterra11(t1,t2,N)
%задание временной сетки h=(t2-t1)/(N-1);
i=1:N; t(i)=t1+h*(i-1); s=t;
%вычисление значений ядра интегрального уравнения
%в узлах временной сетки
fоr i=1:N fоr j=1:N
q(i,j)=Q11_4(t(i),s(j)); end;
end;
%вычисление значений решения интегрального
%уравнения в соответствие с (X.33), (X.34) F=F11_4(t);
F(1)=dF11_4(t(1)); х(1)=F(1)/(h*q(1,1)); for m=2:N
s=0;
fоr j=2:m-1 s=s+q(m,j)*m(j);
еnd;
х(m) = (F(m) -h*s)/( h*q(m,m));
end; Т=t; Z=х;
5. Выполните следующую последовательность команд:
>>t1=1; % левая граница интервала поиска решения
>>t2=1.3;%правая граница интервала поиска решения
>>N=300; % число интервалов разбиения отрезка
%[t1,t2]
>>[Т 2]=Vо1tеrrа11_2 (t1,t2,N) ; % численного
% решения интегрального уравнения Вольтерра
>> рlо1; (Т,Z); % визуализация решения уравнения % Вольтерра (рис. X.7)
|
Рис. X.7. Численное решение интегрального уравнения |
||
t |
+ s2 + 1)x(s)ds = t2 − |
1 |
, полученное при использовании замкнутых |
ò(t 2 |
|||
1 |
|
t |
|
|
квадратурных формул |
||
Приложение
Примеры программ MatLab для численных методов
Программа P1 (итерация неподвижной точки). Получить приближенное решение уравнения х = g(х), начав с предположительно угаданного значения Ро и итерационного правиларп+1 = g(рп)
function [k,p,err,P]=fixpt(g,p0,tol,maxl)
%Вход - g - итерационная функция, вводимая как строка 'g'
%- рО - начальное угаданное значение неподвижной точки
%- tol - допустимое отклонение
%- maxl - максимальный член итерации
%Выход - k - число произведенных итераций
%- р - приближение для неподвижной точки
%- err - ошибка приближения
%- Р - содержит последовательность {рп}
Р(1)= рО; for k=2:maxl
P(k)=feval(g,P(k-l)); err=abs(P(k)-P(k-1); relerr=err/(abs(P(k))+eps); P=P(k);
if (err<tol) I (relerr<tol),break;end end
if k == maxl
disp('максимально допустимое число итераций')
end
Р=Р;
Замечание. Если использовать строго определенную функцию fixpt, то необходимо вводить М-файл g.m в виде строки: 'g' .
Программа P2 (метод деления пополам). Приближенное нахождение корня уравнения f(x) = 0 на интервале [а;b]. Применять только для случая, когда функция f(x) непрерывна и f(a) и f(b) имеют различные знаки.
function [c,err,yc]=bisect(f,a,b,delta)
%Ввод - f - функция вводится как строка 'f'
%- а и b - левая и правая крайние точки
%- дельта - допустимое отклонение
%Выход - с - нуль
%- yc=f(c)
%- err - ошибка вычисления с
ya=feval(f,а); yb=feval(f,b);
if ya*yb>0, break, end maxl=l+round((log(b-a)-log(delta))/log(2)); for k=l:maxl
c=(a+b)/2;
yc=feval(f,c); if yc==0
a=c;
b=c; elseif yb*yc>0
b=c;
yb=yc; else
a=c;
ya=yc; end
if b-a < delta, break, end
end c=(a+b)/2; err=abs(b-a); yc=feval(f,c);
Программа P3 (метод ложного положения или метод regula falsi).
Приближенное нахождение корня уравнения f(x) = 0 на интервале [a; b]. Только для случая, когда функция f(x) непрерывна и f(a) и f(b) имеют различные знаки.
function [c,err,yc]=regula(f,a,b,delta,epsilon,maxl)
%Ввод - f - функция вводится как строка 'f'
%- а и b - левая и правая крайние точки
%- delta - допустимое отклонение для нуля
%- epsilon -допустимое отклонение для значения f в нуле
%- maxl - максимальное число итераций
%Вывод - с - нуль
%- yc=f(c)
%- err - ошибка вычисления для с
ya=feval(f,а); yb=feval(f,b); if ya*yb>0
disp(' Замечание: f(a)*f(b)>0'), break,
end
for k=l: maxl dx=yb*(b-a)/(yb-ya); c=b-dx;
ac=c-a; yc=feval(f,c); if yc==0,break; elseif yb*yc>0
b=c;
yb=yc; else
a=c;
ya=yc; end
dx=min(abs(dx), ac);
if abs(dx)<delta, break, end if abs(yc)<epsilon, break, end
end err=abs(b-a)/2; yc=feval(f,c);
Программа P4 (приближенное нахождение места расположения корней). Найти приблизительное место расположения корней уравнения f(x) = 0 на интервале [а; b] используя точки (xk; f(xk) ) следующий критерий:
(i) (yk-1)(yk) < 0, или
(ii) |yk |< ε и (yk - yk-1)(yk+1 - yk) < 0.
Иначе говоря , либо f(xk-1) и /(xk) имеют различные знаки, либо |f(xk)| мал и тангенс угла наклона кривой у = f(x) меняет знак около (хk , f(xk))
function R = approot (X,epsilon)
%Вход - f - функция записанная как М-файл под именем f .m
%- X - вектор абсцисс
%- epsilon - допустимое отклонение
%Выход - R - вектор приближений корней
Y=f(X);
yrange = max(Y)-min(Y); epsilon2 = yrange*epsilon; n=length(X);
m=0;
X(n+l)=X(n);
Y(n+l)=Y(n);
for k=2:n,
if Y(k-l)*Y(k)<=0, m=m+l;
R(m)=(X(k- 1)+X(k))/2;
end s=(Y(k)-Y(k-l))*(Y(k+l)-Y(k)).;
if (abs(YCk)) < epsilon2) & (s<=0) m=m+l;
R(m)=(k);
end
end
Программа P5 (итерация Ньютона-Рафсона). Найти корень функции f(х) = 0 с одним заданным начальным приближением р0, используяитерацию
pk |
= |
pk −1 |
− |
f ( pk −1 ) |
для k=1,2,3 … |
|
f |
′ |
|||||
|
|
|
|
( pk −1 ) |
|
|
function [p0, err, k, y]=newton(f, df, p0, delta, epsilon, maxl)
%Вход- f - функция, вводимая как строка'f'’
%- df - производная f, вводимая как строка 'df’
%- р0 - начальное приближение функции f к нулю
%- delta - допустимое отклонение для р0
%- epsilon - допустимое отклонение для значений функции у
%- maxl - максимальное число итераций
%- Выход– р0 - приближениеНьютона-Рафсонакнулю
%- err - ошибка вычисления для р0
%- k - число итераций
%- у - значение функции f (р0)
for k=l:maxl
pl=p0-feval(f, р0)/feval(df, p0); err=abs(p1-p0); relerr=2*err/(abs(p1)+delta); p0=p1;
y=feval(f, p0);
if (err<delta)|(relerr<delta)|(abs(y)<epsilon), break, end
end
Программа P6 (метод секущих). Найти корень уравнения f(x) = 0 с двумя заданными начальными приближениями ро, р1 и используя итерацию
pk +1 = pk − |
f ( pk )( pk − pk−1) |
для k=1,2, … |
|
f ( pk ) − f ( pk−1) |
|||
|
|
function [pl,err,k,y]=secant(f, p0, pl, delta, epsilon, maxl)
%Ввод - f - функция, вводимая как строка 'f'
%- р0 и р1 - начальные приближения к нулю
%- delta - допустимое отклонение для р1
%- epsilon - допустимое отклонение для значений функции у
%- maxl - максимальное число итераций
%Выходр1 - приближениекнулюдляметодасекущих
%- err - ошибка вычисления для р1
%- k - число итераций
%- у - значение функции f (p1)
for k=1: maxl;
p2=pl-feval(f, pl)*(pl-p0)/(feval(f, pl)-feval(f, p0)); err=abs(p2-pl);
relerr=2*err/(abs(p2)+delta);
p0=pl;
pl=p2; y=feval(f, pl);
if (err<delta)|(relerr<delta)|(abs(y)<epsilon), break, end
end
Программа P7 (ускоренный метод Стеффенсена). Быстрое нахождение решения уравнения неподвижной точки х = g(х) с заданным начальным приближением р0. Предполагается, что и g(х), и g'(х) непрерывны, |g'(х)| < 1 и обычная итерация неподвижной точки медленно (линейно) сходится кр.
function [p,Q]=steff(f,df,p0,delta,epsilon,maxl)
%Вход - f - функция, вводимая как строка 'f'
%- df - производная, вводимая как строка 'df'
%- р0 - начальное приближение х нулю функции f
