
2790
.pdf
ности и изотропности) пространства. Для незамкнутой системы трансляционные и угловые координаты могут быть циклическими в силу определенной симметрии внешних силовых полей. Например, при движении в центральном (сферическисимметричном) поле, зависящем только от расстояния до некоторого центра, система инвариантна относительно поворота вокруг любой оси, проходящей через этот центр. Угловые обобщенные координаты, описывающие повороты системы вокруг таких осей, будут циклическими, а проекции момента импульса системы на эти оси – интегралами движения (при этом момент импульса, разумеется, должен быть определен относительно начала координат, совпадающем с центром поля).
5.5. Закон сохранения энергии и однородность времени
В общем случае функция Лагранжа может явно зависеть от обобщенных координат, обобщенных скоростей и времени, поэтому ее полная производная по времени имеет вид
Заменяя |
|
|
согласно уравнениям Лагранжа на |
|
|
|
|
, получим |
||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или
71

Величину
называют энергией системы. Согласно соотношению (5.22) мы имеем следующую теорему об изменении энергии:
Покажем, что если наложенные на систему связи голономные и стационарные, а потенциальная энергия U зависит только от координат частиц и возможно времени, то функция E равна сумме кинетической и потенциальной энергий (т.е. совпадает с определением полной механической энергии сис-
темы, данном в п. 1.7.). В указанном случае |
|
|
|
, а кинети- |
|
|
ческая энергия является однородной квадратичной функцией обобщенных скоростей и выражается формулой (3.30). Согласно теореме Эйлера об однородных функциях сумма частных производных такой функции, умноженных на соответствующие переменные, равна самой функции, умноженной на показатель однородности (в нашем случае он равен 2), таким образом
Подставляя (5.26) в (5.24) и учитывая, что |
– , |
получим |
|
72 |
|

Из свойства однородности времени следует, что функция Лагранжа замкнутой системы со стационарными связями не
зависит явно от времени и |
|
Если внешнее поле является |
|
||
стационарным, то функция |
|
также не зависит от времени. По- |
этому из соотношения (5.25) следует закон сохранения энер-
гии: если наложенные на систему связи стационарные и система является замкнутой или движется в постоянном внешнем поле, то функция Лагранжа не зависит от времени явно и энергия системы E является интегралом движения.
Если внешнее поле или связи зависят от времени, то энергия системы не сохраняется: либо совершается работа над системой, либо сама система совершает работу над внешними объектами. Механическая энергия не сохраняется также при наличии трения.
Задачи
5.1Какие проекции импульса и момента импульса будут сохраняться при движении:
а) в поле бесконечной однородной плоскости; б) в поле бесконечной однородной полуплоскости; в) в поле бесконечного однородного цилиндра; г) в поле однородного конуса.
5.2Показать, что при движении частицы в поле цилиндрической однородной винтовой линии, интегралом движения будет величина
где h – шаг винта, и – проекции момента импульса и импульса на ось винта z (см. [2], § 9, задача 3).
73

Часть II. ПРИМЕРЫ ИНТЕГРИРОВАНИЯ УРАВНЕНИЙ ЛАГРАНЖА
§6. Одномерное движение. Задача двух тел
6.1.Движение с одной степенью свободы
Рассмотрим одномерное движение консервативной системы, т.е. движение с одной степенью свободы. В этом случае имеется одна обобщенная координата q, и скорости материальных точек можно записать в виде
Запишем функцию Лагранжа
где
некоторая функция обобщенной координаты, a(q) > 0. В частности, если обобщенной координатой является декартова координата x, то и
Для нахождения закона движения системы с функцией Лагранжа (6.4) достаточно воспользоваться законом сохране-
74

ния энергии E:
Выразим из последнего выражения :
Разделяя переменные и интегрируя, получим
или
где – начальное время, , . Итак, определение закона движения q(t) свелось к квадратуре, т.е. к вычислению интеграла.
В выражении (6.7) можно было оставить интегралы неопределенными, а общее решение записать в виде
где постоянная C |
определяется из начального |
условия |
. Выбор знака перед интегралом, как следует из |
||
(6.6), определяется знаком обобщенной скорости |
в началь- |
|
ный момент времени |
. |
|
75
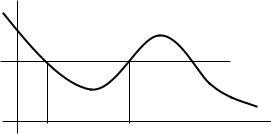
Поскольку и , а величина под корнем в (6.6) должна быть положительной, то движение возможно
только в области пространства, в которой |
(на рис. |
|||
6.1 |
это области между точками A и B и область справа от точки |
|||
C). |
Границы движения |
и |
определяются условием |
|
они называются точками остановки, поскольку обобщенная скорость в них обращается в нуль. Очевидно, при прохождении через точки остановки меняет знак.
Рис. 6.1
Движение, которое происходит в ограниченной области пространства, называют финитным (на рис. 6.1 это движение между точками A и B). Если область, в которой возможно движение, неограниченная или ограничена только с одной стороны, то такое движение называют инфинитным.
Одномерное финитное движение является колебательным
– система совершает периодическое движение между точками остановки и , которые являются корнями уравнения (6.10). В силу обратимости времени движение от точки
до точки |
должно занимать то же время, что и обратное |
|||||
движение от точки |
до точки . Следовательно, период ко- |
|||||
лебаний T будет равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76
6.2. Задача двух тел
Задача о движении системы, состоящей из двух взаимодействующих материальных точек, может быть существенно упрощена путем разложения движения системы на движение ее центра инерции и движения точек относительно последнего.
Потенциальная энергия такой системы зависит только от расстояния между точками, и функция Лагранжа имеет вид
Введем вектор
и поместим начало координат в центре инерции, тогда
Из двух последних равенств получим
Тогда функция Лагранжа может быть записана в виде, аналогичном функции Лагранжа системы из одной точки, движущейся во внешнем потенциальном поле U(r):
где величина , равная
называется приведенной массой. Соотношение (6.16) можно также записать в виде
77

Таким образом, задача о движении двух взаимодействующих точек сводится к задаче о движении одной точки массой во внешнем поле U(r), зависящем только от расстояния r до центра инерции. Решение задач о движении частицы в подобных полях, называемых центральными, рассматривается далее.
Заметим, что задача о движении трех взаимодействующих тел в общем случае не может быть решена аналитически.
Задачи
6.1. Найти закон движения частицы в потенциальном поле
(потенциал Морзе, рис. 6.2, а)
([12], задача 1.1, а).
6.2. Найти закон движения частицы в потенциальном поле
, см. рис. 6.2, б ([12], задача 1.1, в).
а |
б |
|
Рис. 6.2 |
6.3. Найти закон движения плоского маятника массы m и длины l в поле силы тяжести, если в нижней точке его кинетическая
энергия равна |
([12], задача 1.6). |
|
78 |

§ 7. Движение в центральном поле
7.1. Движение частицы в центральном поле
Рассмотрим задачу о движении одной частицы в центральном поле – т.е. в таком поле, в котором потенциальная энергия частицы зависит только от расстояния r до некоторой точки (центра поля). При этом на частицу будет действовать центральная сила, направленная вдоль радиус-вектора r, проведенного из центра, ее модуль зависит только от расстояния r до центра:
здесь отношение , очевидно, представляет собой единичный вектор, направленный вдоль .
Центральное поле обладает сферической симметрией, поэтому, как было показано ранее (см. п. 5.4), момент импульса , определенный относительно центра поля, будет сохраняющейся величиной. Это легко видеть также из уравнения
моментов (1.31). Так как для центрального поля векторы и
коллинеарны, то момент силы |
и |
. |
|
Так как вектора |
и всегда взаимно перпендикулярны, |
||
постоянство вектора |
будет означать, что вектор |
(а следова- |
|
тельно и траектория движения частицы) всегда будет оставаться в одной плоскости, перпендикулярной . Если в этой плоскости ввести полярные координаты , , функция Лагранжа запишется в виде (см. формулу (3.36)):
Координата вполне ожидаемо является циклической. Соответствующее ей уравнение Лагранжа будет иметь вид
79
откуда следует, что обобщенный импульс будет интегралом движения. Согласно формуле (5.20), этот обобщенный импульс представляет собой ни что иное, как проекцию момента импульса на ось поворота . Мы выбрали полярную систему координат таким образом, что ось z направле-
на вдоль L, поэтому проекция |
равна модулю момента им- |
пульса : |
|
|
|
|
|
. |
|
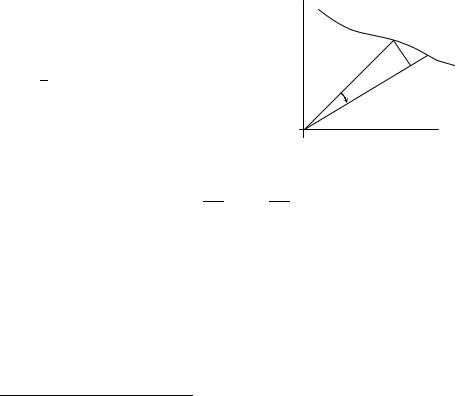
В рассматриваемой задаче закон со- |
|
||||
хранения момента импульса |
допускает |
|
|||
следующую геометрическую |
интерпре- |
|
|||
тацию. Как видно из рис. 7.1, |
величина |
|
|||
представляет |
собой |
пло- |
|
||
щадь сектора, образованного двумя бес- |
|||||
|
|||||
конечно близкими радиус-векторами и |
|
||||
элементом дуги траектории. Перепишем |
|
||||
выражение (7.4) в виде |
|
|
|
Рис. 7.1 |
|
Из соотношения (7.5) заключаем, |
что постоянство эк- |
|
вивалентно постоянству величины |
|
, называемой сек- |
|
||
ториальной скоростью. Таким образом мы пришли к хорошо известному второму закону Кеплера (интегралу площадей)1: при движении точки в центральном поле ее радиус-вектор за равные промежутки времени описывает равные площади.
Запишем теперь второе уравнение Лагранжа, соответст-
1 Три закона Кеплера представляют собой эмпирические соотношения, сформулированные Иоганном Кеплером в начале XVII в. на основе анализа астрономических наблюдений Тихо Браге за движением планет. Позднее И. Ньютон математически показал, что законы Кеплера напрямую следуют из закона всемирного тяготения и основных законов механики.
80
