
2790
.pdf
Общее решение линейного неоднородного дифференциального уравнения (8.18) есть сумма , где - общее решение соответствующего однородного уравнения, а
– любое частное решение неоднородного уравнения. В дан-
ном случае |
- свободные колебания. |
|
Рассмотрим важный частный случай внешней силы |
, |
|
когда она является периодической функции времени, изменяющейся с частотой :
Частное решение уравнения (8.18) будем искать в виде периодической функции , в результате подстановки которой в уравнение получим Итак, общим решением уравнения (8.18) будет функция
представляющая собой сумму двух колебаний: с собственной частотой и частотой вынуждающей силы . Отметим, что при наличии малого трения в системе первое слагаемое со временем исчезнет (установившиеся колебания). Постоянные и определяются из начальных условий.
Когда колебания происходят в фазе с вынуждаю-
щей силой |
(т.к. |
|
), а |
|
при |
– в |
противофазе |
|
|
. На рис. 8.1 показана |
|
|||
зависимость |
амплитуды |
вынуж- |
|
|
денных колебаний b |
от |
частоты |
Рис. 8.1 |
|
|
|
|
101 |
|
вынуждающей силы . |
|
|
Решение (8.20) не применимо в случае |
. При |
|
амплитуда |
. Явление резкого возрастания |
амплитуды |
вынужденных колебаний при совпадении частоты вынуждающей силы с собственной частотой колебаний системы называют резонансом. На практике беспредельному возрастанию амплитуды при резонансе препятствуют нелинейные эффекты, не учитываемые в рамках рассматриваемой нами теории малых гармонических колебаний, а также имеющиеся в любой в реальной системе силы сопротивления.
Чтобы выяснить характер колебаний системы при при-
ближении к резонансу, положим, что |
|
, где – малая |
|
величина, и запишем общее решение в комплексной форме: |
|||
Поскольку |
величина |
слабо изменяется в те- |
|
чение периода |
колебаний множителя |
. Следовательно, |
|
движение вблизи резонанса можно считать малыми колебаниями с переменной амплитудой, равной
Записав комплексные амплитуды и в виде
получим
102

Из последнего выражения следу- |
|
|
ет, что амплитуда |
будет совер- |
|
шать колебания с |
частотой в |
|
пределах |
|
|
(рис. 8.2). Данное явление назы- |
|
|
вают биениями. |
|
|
Найдем теперь общее реше- |
Рис. 8.2 |
|
ние уравнения (8.18) в случае |
|
|
произвольной силы |
. Перепишем его в виде |
|
Введя комплексную функцию
вместо уравнения второго порядка (8.18) получим комплексное уравнение первого порядка
Решением |
соответствующего однородного |
уравнения |
(когда правая часть в (8.27) равна нулю) будет |
, где |
|
постоянная. Решение неоднородного уравнения будем ис- |
||
кать в виде |
(метод вариации произвольной посто- |
|
янной). Тогда получим |
|
|
Функция находится интегрированием этого уравнения от 0 до t. Общее решение уравнения (8.27) запишется в виде
103

где |
|
Из соотношения (8.26) следует, |
||||
что искомая функция |
|
|
|
таким образом |
||
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь первые два слагаемых описывают свободные колебания,
атретье – вынужденные.
8.3.Затухающие колебания
Влюбой реальной системе, совершающей колебания, присутствуют силы сопротивления, приводящие к диссипации энергии и постепенному уменьшению амплитуды (затуханию) колебаний. Мы ограничимся рассмотрением силы трения, имеющей вид
т.е. пропорциональной обобщенной скорости . Такой характер носит сила трения, действующая на движущееся с невысокой скоростью тело в газе или жидкости.
Рассмотрим сначала случай свободных затухающих колебаний. Сила (8.31) не является потенциальной, соответственно уравнением движения будет уравнение Лагранжа для неконсервативной системы (3.12). В нашем случае оно запишется в виде
104

или
где |
|
|
|
– частота свободных колебаний без трения, |
|
|
– коэффициент затухания. |
||
|
|
|||
|
Частное решение уравнения (8.33) будем искать в виде |
|||
|
|
, тогда получим для характеристическое уравнение |
||
корни которого
Если |
, то корни |
оказываются комплексными: |
|||
|
|
|
|
|
|
и, как известно из курса высшей математики, общее решение уравнения (8.33) запишется в виде
Происходящее по |
такому |
|
||
закону движение, называе- |
|
|||
мое |
затухающими |
колеба- |
|
|
ниями, можно рассматривать |
|
|||
как |
гармонические |
колеба- |
|
|
ния, |
амплитуда |
которых |
|
|
экспоненциально убывает со |
|
|||
временем (рис. 8.3). Отме- |
|
|||
тим, что «частота» затухаю- |
|
|||
щих |
колебаний |
меньше |
Рис. 8.3 |
|
частоты |
гармонических ко- |
|
||
лебаний |
в отсутствии трения. |
|
||
105

Помимо коэффициента затухания , используют и некоторые другие характеристики затухающих колебаний. Величину называют временем релаксации, она представляет собой время, в течение которого амплитуда колебаний уменьшится в e раз. За это время система совершает колебаний.
Декрементом затухания называется отношение двух соседних амплитуд, равное
где |
период колебаний. |
|
Величину |
называют логарифмическим декрементом затухания.
Добротностью колебательной системы называют отношение энергии колебаний к потерям энергии за период, умноженное на . Так как энергия пропорциональна квадрату амплитуды, получим
В случае слабого затухания (высокой добротности), когда
, |
|
и добротность будет равна |
|
Если |
, то корни |
оказываются действительны- |
106
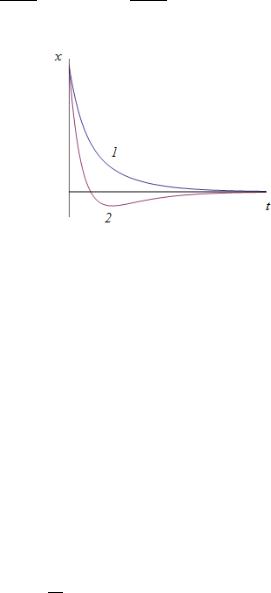
ми и общее решение имеет вид
где |
и |
– действительные |
|
|||
постоянные, определяемые из |
|
|||||
начальных |
|
условий. |
График |
|
||
функции |
|
в зависимости |
|
|||
от соотношения между коэф- |
|
|||||
фициентами |
и |
может |
|
|||
иметь |
несколько различный |
|
||||
вид (см. кривые 1 и 2 на рис. |
|
|||||
8.4.). Таким образом, при |
|
|||||
достаточно |
большом |
трении |
Рис. 8.4 |
|||
( |
) колебания возникать |
|||||
|
||||||
не будут, |
выведенная из по- |
|
||||
ложения равновесия система будет асимптотически возвра-
щаться в это положение ( |
). Такое движение называют |
||
апериодическим затуханием. |
|
|
|
Наконец, в предельном случае |
корни характери- |
||
стического |
уравнения вещественны и |
равны друг другу |
|
( |
), и общее решение будет иметь вид |
||
Эта функция также описывает апериодическое затухание.
8.4. Вынужденные колебания при наличии трения
Рассмотрим малые одномерные колебания под действием вынуждающей силы вида (8.19) при наличии трения. Уравнение движения будет иметь вид
107

Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его об-
щим решением будет сумма |
, где |
- общее решение |
|
соответствующего однородного уравнения, а |
– любое част- |
||
ное решение неоднородного уравнения. Функция |
есть об- |
||
щее решение уравнения (8.33) свободных (в отсутствии вынуждающей силы) затухающих колебаний, т.е. она определяется выражением (8.37), (8.42) или (8.43). Функция будет описывать вынужденные колебания.
Решение уравнения (8.44) удобно искать в комплексном виде. Для этого заменим уравнение (8.44) уравнением
Поскольку данное уравнение линейно и , действительная часть его решения будет решени-
ем исходного уравнения (8.44). |
|
Будем искать частное решение в виде |
, где |
– комплексная амплитуда. После его подстановки
получим
Преобразовав это комплексное число к показательной форме, найдем
Заметим, что мнимая часть числа B всегда отрицательна, а действительная часть изменяет знак с плюса на минус (при
108
увеличении от 0 до ) в точке . Поэтому угол
отрицателен и лежит в пределах от 0 до – .
Итак, частным решением уравнения (8.44) будет функция
Добавляя общее решение соответствующего однородного уравнения (выберем решение (8.37) для случая ) получим общее решение
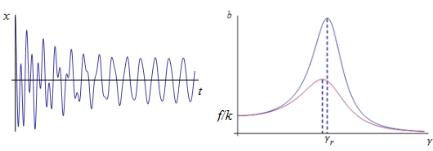
Первое слагаемое (затухающие колебания) экспоненциально убывает со временем и через некоторый период остаются только вынужденные колебания, происходящие по гармоническому закону (8.46). Такие колебания называют установивши-
мися (см. рис. 8.5).
Рис. 8.5 Рис. 8.6
Зависимость амплитуды вынужденных колебаний b частоты вынуждающей силы (резонансная кривая) при различных значениях коэффициента затухания представлена на рис. 8.6. Резонансная частота , соответствующая максимуму амплитуды b, находится путем приравнивания нулю произ-
109
водной от подкоренного выражения в соотношении (8.47):
Если затухание мало ( ), то . Максимальное значение амплитуды вынужденных колебаний равно
Так как |
|
|
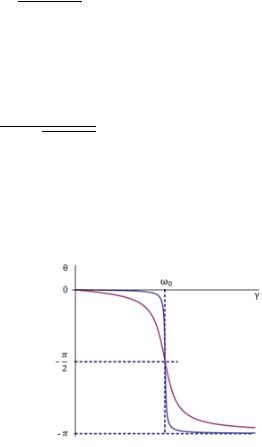
вынужденные колебания отстают по фазе |
|||
от вынуждающей силы на угол |
, который зависит от соот- |
|||||
ношения между частотой собственных колебаний |
и часто- |
|||||
ты колебаний вынуждающей силы |
(см. рис. 8.7). При |
|||||
сдвиг фаз |
, |
а при |
|
|
||
сдвиг |
фаз |
|
. |
В первом |
|
|
случае |
колебания |
происходят |
|
|
||
почти в фазе с вынуждающей |
|
|
||||
силой, а во втором – почти в |
|
|
||||
противофазе. Сдвиг фаз скач- |
|
|
||||
ком изменяется |
на величину |
|
|
|||
при |
|
(вблизи резо- |
|
|
||
нанса), чем выше коэффициент |
|
|
||||
затухания , |
тем |
более «раз- |
|
|
||
мыт» такой переход. |
Рис. 8.7 |
|
||||
8.5. Малые колебания системы с многими степенями свободы
Рассмотрим консервативную систему с s степенями сво-
боды, потенциальная энергия которой |
имеет |
|
минимум при |
. Условия минимума |
|
110
