
2790
.pdfДанные соотношения можно записать в матричной форме:
или, сокращенно,
Запишем аналогичные соотношения для обратного преобразования из «штрихованной» системы в «нештрихованную»:
где – транспонированная матрица A. |
|
|||
|
Элементы |
не являются независимыми друг от друга. |
||
Каждая строка матрицы A есть совокупность направляющих |
||||
косинусов прямой линии (одной из осей |
) относительно |
|||
осей |
, |
, |
. Как известно, в ортогональной системе ко- |
|
ординат для любого вектора сумма квадратов направляющих косинусов равна единице, поэтому
141
Каждая пара строк матрицы A содержит направляющие косинусы двух взаимно-перпендикулярных осей «штрихованной» системы относительно осей , , . Поэтому, приравнивая нулю скалярные произведения соответствующих векторов, получим еще три условия
Соотношения (11.15) и (11.16) можно объединить в одно выражение
где – символ Кронекера:
Соотношение (11.17) называют соотношением ортогональности, а удовлетворяющие этому условию линейные преобразования координат (11.12) называют ортогональными. Условия ортогональности (11.17) содержат шесть соотноше-
ний, |
соответствующих |
различным |
значениям индексов |
||
|
. Поэтому, из девяти элементов , как и следова- |
||||
ло ожидать, независимыми остаются лишь три. |
|||||
|
Каждый столбец матрицы A содержит направляющие ко- |
||||
синусы одной |
из осей |
, |
, |
относительно осей |
|
, |
, |
. Повторяя те же рассуждения, что и для строк |
|||
матрицы A, можно прийти к условию ортогональности
которое, однако, не является независимым от (11.17). Рассмотрим теперь матрицу , обратную к матрице
преобразования A. По определению,
142
где – единичная матрица:
Вычисляя произведение матриц |
, получим |
где через обозначены элементы матрицы . Для выполнения условия ортогональности (11.17) следует положить
. Таким образом, условие ортогональности преобразования (ортогональности матрицы A) может быть записано в виде
или
Используя свойства определителя матрицы, в соответствии с (11.24) получим
следовательно, определитель ортогональной матрицы может принимать только два значения: +1 и –1. Чтобы выяснить геометрический смысл этих значений, рассмотрим две матрицы преобразования:
Очевидно, , . Первая матрица задает
тождественное преобразование, которое оставляет оси неиз-
менными. Вторая матрица изменяет направление оси |
на |
143 |
|
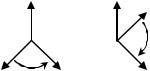
противоположное ( , остальные оси не изменяются. Напомним, что координатная система называется правой, если из конца третьей оси кратчайший поворот от первой оси ко второй виден совершающимся против часовой стрелки. В противном случае система координат называется левой. При преобразовании, соответствующем матрице , происходит изменение правой системы коорди-
нат на левую и наоборот (рис. |
|
|
11.3). Подобное изменение сис- |
|
|
темы координат может проис- |
|
|
ходить только в результате |
|
|
операции отражения или ин- |
|
|
версии, его невозможно дос- |
|
|
тичь непрерывными поворота- |
Рис. 11.3 |
|
ми координатной системы. |
|
|
Итак, ортогональное преобразование при |
озна- |
|
чает непрерывные повороты системы координат (оси при этом остаются взаимно перпендикулярными). Именно такие преобразования соответствуют изменению ориентации твердого тела. При преобразование, помимо поворота системы, включает операцию отражения или инверсии, при этом правая координатная система преобразуется в левую, а левая – в правую. Такие преобразования не могут соответствовать реальному движению твердого тела.
11.2.Углы Эйлера
Вкачестве трех независимых параметров, которые однозначно определяют ориентацию твердого тела и могут быть выбраны в качестве обобщенных координат, чаще всего ис-
пользуют углы Эйлера , и . Рассмотрим, как они определяются.
Пусть в начальный момент времени оси неподвижной (K) и подвижной (K') систем координат совпадают. Начала координат будем полагать всегда совпадающими, поскольку мы сейчас рассматриваем только взаимную ориентацию осей (т.е.
144
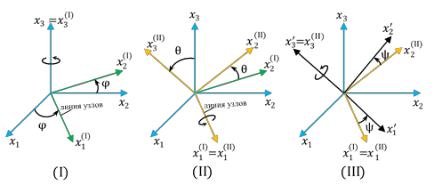
будем считать, что тело имеет одну фиксированную точку, совпадающую с началом O' подвижной системы). Произвольный поворот твердого тела и жестко связанной с ним системы координат K' можно представить как результат трех последовательных плоских поворотов вокруг координатных осей (при этом два последовательных поворота должны осуществляться вокруг разных осей). Обычно используют следующую последовательность поворотов (рис. 11.4):
1) поворот против часовой стрелки вокруг оси на угол , оси координат системы K' после этого поворота обозначим
как |
, |
, |
|
; |
|
|
|
2) поворот против часовой стрелки вокруг оси |
на |
||||
угол , оси координат системы K' после этого поворота обо- |
||||||
значим как |
|
, |
, |
; |
|
|
|
3) поворот против часовой стрелки вокруг оси |
на |
||||
угол . |
|
|
|
|
|
|
|
Рис. 11.4 |
|
|
Линию пересечения координатных плоскостей |
и |
||
систем K и K' называют линией узлов, эта линия совпадает |
|||
с осью |
(промежуточным положением оси |
после первого |
|
поворота). |
|
|
|
Итак, |
угол есть угол между осью |
и линией узлов, |
|
145
угол – угол между осями |
и , и угол |
– угол между ли- |
||
нией узлов и осью . Углы |
и |
|
|
представляют собой |
|
||||
сферические координаты (полярный и азимутальный углы) оси
относительно неподвижных осей |
, |
, , угол опреде- |
ляет положение двух других осей: |
и |
. Чтобы повороту со- |
ответствовала однозначная совокупность значений эйлеровых углов, принимается, что значения углов и лежат в пределах от 0 до , а угла – от 0 до .
Составим матрицы преобразования для каждого из трех поворотов указанной последовательности:
Преобразования координат после каждого из поворотов можно записать в матричной форме следующим образом:
Результирующий поворот
соответствует матрице A, равной произведению матриц трех последовательных поворотов:
146
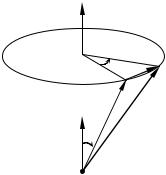
11.3. Бесконечно малый поворот. Теорема Эйлера
|
Рассмотрим |
поворот радиус- |
|
|
||||
вектора |
на бесконечно малый угол |
|
|
|||||
d |
вокруг некоторой оси, направлен- |
|
|
|||||
ной |
вдоль |
единичного вектора |
и |
|
|
|||
проходящей через начало координат |
|
|
||||||
. |
Пусть |
поворот |
осуществляется |
|
|
|||
против часовой стрелки, если смот- |
|
|
||||||
реть с конца вектора |
(рис. 11.5). |
|
|
|
||||
|
Вектор |
|
перпендику- |
|
|
|||
лярен векторам |
и |
и направлен со- |
|
|
||||
ответствии с правилом правого винта |
Рис. 11.5. |
|||||||
при повороте от |
к |
, а его модуль |
||||||
|
|
|||||||
равен
Поэтому, в соответствии с определением векторного произведения векторов, мы можем записать
где вектор |
определяется как |
При повороте вектора его компоненты изменяются таким же образом, как они изменялись бы при повороте системы координат (сам вектор при этом не изменяется) вокруг
147
той же оси, но в противоположном направлении. Поэтому,
формула (11.32) соответствует повороту координатной системы вокруг оси n по часовой стрелке. При повороте системы координат против часовой стрелки получим
В координатной форме записи это соотношение примет вид
Отсюда можно получить матрицу бесконечно малого поворота:
где E – единичная матрица (11.21), а – антисимметричная матрица, содержащая три независимых бесконечно малых па-
раметра |
, полностью определяющих беско- |
нечно малый поворот: |
|
Конечным поворотам, в отличие от бесконечно малых, нельзя поставить в соответствие некоторый вектор. Действительно, если двум конечным поворотам можно было бы поставить в соответствие два вектора и , то результат этих поворотов не зависел бы от той последовательности, в которой они осуществляются, поскольку сумма векторов коммутативна:
. Но, как мы выяснили ранее, результат двух поворотов описывается произведением соответствующих матриц
148

поворота и , и при этом в общем случае , т.е. данный результат зависит от последовательности, в которой осуществлялись эти два поворота.
Покажем теперь, что матрицей вида (11.36) можно описать произвольное бесконечно малое собственное ортогональное преобразование. Так как при таком преобразовании координаты изменяются бесконечно мало, мы можем представить
соответствующую матрицу перехода в виде |
, где |
матрица содержит девять бесконечно малых элементов |
: |
Далее, ограничиваясь членами первого порядка малости, мы можем записать
откуда следует, что |
. Отсюда |
видно, что |
матрица должна быть антисимметрична ( |
, т.е. в |
|
общем случае она может быть записана в виде (11.37).
Итак, произвольное бесконечно малое ортогональное преобразование представляет собой бесконечно малый поворот вокруг некоторой оси n. Поскольку любое конечное преобразование может быть представлено как совокупность одинаковых последовательных бесконечно малых преобразований, оно также будет являться поворотом вокруг некоторой оси. На основании этих рассуждений мы приходим к одной из важных теорем кинематики твердого тела – теореме Эйлера о вращении1: если твердое тело имеет одну неподвижную точку, то его произвольное перемещение можно осуществить единственным поворотом вокруг некоторой подходящей оси, проходящей через данную точку.
Если тело не имеет фиксированной точки, появляются
1 Строгое доказательство этой теоремы приведено в [1], п. 4.6.
149
три дополнительные степени свободы, соответствующие поступательному движению твердого тела (движению начала O' подвижной системы координат K' относительно неподвижной системы K). Таким образом, произвольное перемещение твердого тела может быть представлено как совокупность параллельного переноса и поворота вокруг некоторой оси.
11.4. Угловая скорость
Рассмотрим произвольное бесконечно малое перемещение твердого тела, произошедшее за промежуток времени .
Приращение |
радиус-вектора произвольной точки P твер- |
|
дого тела будет складываться из перемещения dR начала |
||
подвижной системы координат и перемещения |
, пред- |
|
ставляющего собой бесконечно малый поворот вокруг некото-
рой оси, проходящей через точку : |
|
||
Разделив это равенство на |
, получим |
|
|
где |
есть скорость рассматриваемой точки P относитель- |
||
но внешней неподвижной системы координат, |
– ско- |
||
рость точки и |
– угловая скорость твердого тела. |
||
|
Рассмотрим также связь между скоростями изменения |
||
произвольного вектора |
, которые наблюдаются в подвиж- |
||
ной и неподвижной системах координат. Изменение |
этого |
||
вектора за время , наблюдаемое в неподвижной системе координат , будет равно сумме изменения этого вектора за тоже время, наблюдаемого в движущейся вместе с телом сис-
теме координат , и изменения |
, обусловленного по- |
|
воротом тела на угол |
: |
|
150
