Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Интегральное исчисление: практикум. Пантелеев И.Н

.pdf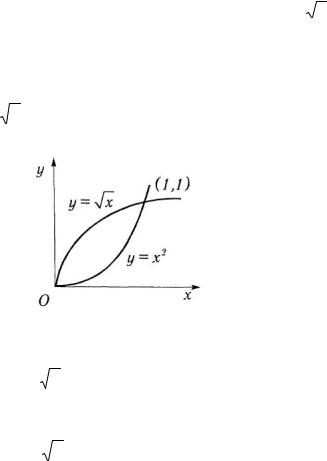

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2416 17 18 19 20 21 22 23 24 > Следующая >>>

a 4

11 ö

a 4

Il = Il

+ Il

		6.6. Найти		статический момент			и	момент		инерции
фигуры,			ограниченной			линиями y = x 2		и	y =	x
относительно оси абсцисс.
		Решение. Плоская фигура, ограниченная заданными
линиями,			показана		на	рис. 3.44. Ширина		сечения		на
расстоянии			y	по	оси x	определяется	разностью		абсцисс
x	2	(y)- x (y)= y - y 2 .
		1

Статический момент определяем по формуле

Рис.3.44

1	2	æ	2		5		y 4	ö	1	3


mx = ò0 y(	y - y )dy =	ç		y	2			÷
		ç				-		÷		= .
		è	5				4	ø	0	20

Момент инерции находим по первой из формул (10)

1 2	2	æ	7		7		y 5 ö		1	3


I x = ò0 y (	y - y )dy =	ç		y	2			÷
		ç				-		÷		= .
		è	2				5	ø	0	35

6.7. Найти статический момент относительно основания: а) кругового конуса; б) полусферы; в) поверхности

кругового конуса; г) поверхности полусферы.

Решения. а) Расположим оси координат относительно конуса, как показано на рис. 3.45. Из подобия треугольников

151

		H			R		æ		x ö
OAB и	MNB имеем			=		, y =	Rç1	-		÷	. Статический
					y
		H - x					è		H ø
момент	относительно		плоскости				основания находим по
формуле (5)

Рис. 3.45

myz = p ò0

dx = pR

ò0

ç x

÷dx =

æ x 2

x 4

pR 2 H 2

= pR

- 2

б) Расположим оси координат относительно полусферы, как показано на рис. 3.46. Из треугольника OMN имеем y 2 = R 2 - x 2 . Статический момент относительно плоскости основания вычисляем по формуле (5)

Рис. 3.46

152

2 x 2

x 4 ö

pR 2

myz = p ò0

xy dx = p ò0

x(R - x )dx = p ç R

в) Поскольку поверхность кругового конуса представляет

поверхность	вращения	вокруг осиOx	(рис. 3.45), то
статический	момент	относительно	плоскости	основания
вычисляем по формуле (6)

H myz = 2p ò0

= 2pR H

xy 1 + y¢2 dx = 2p ò0H

2		2	æ x 2			x 3
H	+ R		ç		-
H	+ R		ç	2	-	3H
			è	2		3H

	æ	-	x	ö	1	æ	R ö	2
xRç1		-	H	÷	1	+ ç ÷		dx =
	è		H	ø		è	H ø
ö H		pRH				2	2
÷	=				h	+ R .
÷	=		3		h	+ R .
ø 0			3

г) Статический момент поверхности полусферы (рис. 3.46)

относительно плоскости основания вычисляем по формуле (6)

myz = 2p ò0R xy 1 + y¢2 dx .

Производную y¢ находим из дифференцирования выражения

y 2 = R 2		- x 2 : 2 yy¢ = -2x ,				y¢ = -	x	. Радикал под
знаком интеграла примет вид							R 2 - x 2
знаком интеграла примет вид
1 + y	¢2			x 2		R
1 + y		=	1 +	R 2 - x 2 =		R2 - x 2 .
Таким образом,
	myz		= 2p	R x R 2 - x 2			R	dx = 2pR R 2	= pR 3 .
				ò0		R 2 - x 2		2
6.8.		Найти.			Заданная		цилиндрическая			поверхность
показана на рис. 3.47.

Статические моменты находим по формулам(7), учитывая, что

153

	z = y, x 2 + y 2 = R 2 , y¢ = -						x		,
						R 2 - x 2
		dl =	1 + y¢2 dx =			Rdx .
						R2 - x 2
myz	=	R		R	Rdx	=	R	R	xdx = 0 .
myz	=	xzdl =		xy		=	R		xdx = 0 .
		ò-R		ò-R	R2 - x 2			ò-R
mzx =	R	yzdl =	R	y 2	Rdx	= R	R		R 2 - x 2 dx .
	ò-R		ò-R		R 2 - x 2		ò-R

Рис. 3.47

Интегрируя по частям, будем иметь

R æ

mzx

+ R ò-R

ç x R - x

- x

R æ

- x

+ R

arcsin

x ö R

ç x

R ø -R

1 R

Rdx

mxy

2 ò-R

R 2 - x2

ò-R

Используя вычисления предыдущего интеграла, получим

mxy = p R 3

154

6.9. Найти			x 2	y 2
	момент	инерции	эллипса+		= 1
	момент	инерции	эллипса+	b 2	= 1
			a 2	b 2

относительно его осей.

Решение. Поскольку эллипс симметричен относительно координатных осей, то достаточно найти момент инерции части эллипса, расположенной в первом квадрате, и умножить

результат

на 4.

Согласно

формулам (10)

будем

иметь

a b 2

I y

= 4

ò0

- x x dx .

Делаем

замену x

= a sin t ,

тогда

dx = a cos tdt

I y

2 a cos ta2 sin2 ta cos tdt =

ò0

p 2

a3b

p 2

(1- cos 4t )dt

a3b

= a

bò0

sin

2tdt =

ò0

p .

Аналогично находим момент инерции относительно оси x

b a

I x

= 4

ò0

- y

y dy .

Делаем

замену y

= b sin t ,

тогда

dy = b costdt

I x

b cos tb

sin

tb costdt

p .

b ò0

6.10. Найти момент инерции: а) цилиндра; б) конуса относительно его оси, высота которого H, а радиус основания

R .

Решение.		) а Разобьём	цилиндр				на	элементарные
цилиндрические трубки параллельно оси цилиндра (рис. 3.48).
Объём	такой	элементарной		трубкиV = 2pyHdy ,					где
y - радиус трубки толщиной dy и высотой H .
Момент инерции элементарной трубки относительно оси
равен dI x	= 2pHy 3 dy .
Суммируя,		получим	момент				инерции		цилиндра
относительно его оси					1
	I x	= ò0R dlx = 2pH ò0R y 3dy =			1	pHR 4 .
	I x	= ò0R dlx = 2pH ò0R y 3dy =				pHR 4 .
				2

155

		Рис. 3.48
б)	Разобьём конус на		элементарные							цилиндрические
трубки	параллельно	оси		конуса(рис. 3.49). Объём
элементарной трубки		равенdV = 2pyhdy ,							где	y - радиус
трубки толщиной dy и высотой h . Из подобия треугольников
				æ		y ö
OAB и	MNB находим,	что h =	H ç1 -					÷ .	Момент инерции
OAB и	MNB находим,	что h =	H ç1 -					÷ .	Момент инерции
элементарно трубки				è		R ø
элементарно трубки				y ö
		æ		y ö		3
	dlx	= 2pH ç1	-		÷y		dy .
	dlx	= 2pH ç1	-		÷y		dy .
		è		R ø

Рис. 3.49

Суммируя, получим момент инерции конуса относительно его оси

R æ

y 4 ö

y 4

y5 ö

= 2pH

ò0

ç y

÷dy = 2pH ç

pHR

ò0

5R ø

6.11. Найти момент инерции боковой поверхности: а) цилиндра, высота которого H , а радиус основанияR ,

156

относительно его оси; б) шара радиуса R относительно его диаметра.

Решение. )а Масса элементарной полости боковой поверхности цилиндра (рис. 3.50) на расстоянии R от оси вращения есть d 2pRdx .

Рис. 3.50

Момент инерции элементарной плоскости относительно

оси Ox равен dlx = R 2d 2pRdx .

Суммируя, получим момент инерции цилиндрической поверхности, высота которой H

H H

I x = ò0 dI x = 2pdR3 ò0 dx = 2pdR3 H = mR 2 ,

где m = 2pdRH - масса боковой поверхности цилиндра.

б) Рассечём поверхность шара двумя параллельными плоскостями, отстоящими друг от друга на расстоянии dx , и параллельными плоскостями Oyz (рис. 3.51).

Масса	элементарной	плоскости боковой	поверхности
шара на	расстоянии y от	диаметра, расположенного	по оси
Ox , есть d 2pydl .

157

Рис.3.51

Момент инерции элементарной полоски относительно

диаметра равен dI x = y 2d 2pydl . Суммируя,

получим

момент

инерции поверхности шара относительно его диаметра

I x = ò-RR dI x = 2pd ò-RR y 3 dl .

Учитывая,

что

x 2 + y 2

= R 2 ,

y =

R 2 - x 2 ,

¢2

Rdx

= -

r 2 - x 2 ,

dl = 1 + y

dx = R 2 - x 2 ,

находим

2pdR

ò-R

(R 2

- x 2 )dx = 2pdRçR 2 x

pdR 4 =

mR 2 ,

-R

где m = 4pdR2 - масса поверхности шара.

3.7. Координаты центра тяжести

Точка C , являющаяся центром параллельных сил тяжести частиц, называется центром данного тела.

1°. Для материальной дугиAB плоской кривой прямоугольные координаты центра тяжести определяются по формулам

158

òd (M )xdl

òd (M ) ydl

x =

; y =

;

(1)

òd (M )xdl

где т — масса

АВ;

mx, my -

дуги

статические

моменты

этой дуги относительно осей х, y; δ(М) —линейная плотность

распределения

массы

в точкеМ(х,

у); dl

— дифференциал

дуги.

Декартовы координаты центра тяжести дуги кривойL,

уравнение	которой задано в			полярной				системе	координат,
d = d (j) , определяются по формулам
	x =	1	j2 r cosj dL;	y =	1	j2	r sin j dL;		(2)
	x =		j2 r cosj dL;	y =		j2	r sin j dL;		(2)
	c	L jò		c	L jò
	c			c
		1			1
								j2
где dL =	r2 + r¢2 dj - дифференциал дуги;							dL = òdL - длина
								j1

дуги. Здесь плотность дуги принята равной единице.

2°. Координаты центра тяжести криволинейной трапеции, прилежащей к оси Ох, определяются по формулам

òd (M )xydx

òd (M ) y2dx

x =

;

(3)

òd (M ) ydx

где m — масса плоской

фигуры; mx, mу — статические

моменты этой фигуры относительно осей х, у.

3°. Если плоская фигура

ограничена

линиями у1 = f1(x);

у2 =f2(x); x=a; x=b, то координаты центра тяжести

определяются по формулам

òd (M )x( f2 (x) - f1 (x))dx

òd (M )( f2 2 (x) - f12 (x))dx

xc =

(4)

òd (M )x( f2 (x) - f1 (x))dx

159

Здесь δ(М) — поверхностная плотность, т. е. масса единицы площади поверхности фигуры.

Если плотность δ(М) постоянна, то в предыдущих формулах δ может быть вынесена за знак интегралов и на ее величину можно сократить.

Если однородная материальная линия или фигура имеет ось симметрии, то центр тяжести лежит на этой оси.

Координаты центра тяжести криволинейного сектора,

ограниченного				двумя полярными		радиусами и			кривойr =
δ(φ), определяются по формулам
		x =	1	j2	r3 cosj dj , y =	1	j2	r3 sinj dj ,	(5)
			1			1
			3S jò			3S jò
		c			c

				1		1
	1	j2
где S =	1	ò p2dj - площадь сектора.
где S =		ò p2dj - площадь сектора.
	2 j
		1

4°. Расстояние xc центра тяжести тела от данной плоскости находится по формуле

		b		b
	xc = ò xSdx / òSdx ,						(6)
		a		a
где S(x)dx — объем элементарного слоя тела на расстояниих
от плоскости; S(x) — площадь сечения						тела	плоскостью
параллельной данной плоскости и отстоящей от								нее на
расстоянии х.						кривой y = f(x)
Для	тела, образованного			вращением		кривой y = f(x)
(a £ x £ b)	вокруг оси х,	расстояние хC центра					тяжести	от
плоскости yOz определяется по формуле
			b
			ò xy2dx
	x	=	a		.		(7)
	x	=	b		.		(7)
	c		b

ò y2dx

Расстояние хC центра тяжести поверхности вращения от плоскости, перпендикулярной оси x, опредляется по формуле

160

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2416 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]