
2595
.pdf
датчика равномерно распределенных случайных чисел.
2.Перечислите наиболее часто встречающиеся на практике законы распределения дискретных случайных величин. В каких задачах они используются?
3.Как может быть реализовано моделирование дискретной случайной величины на основе датчика равномерно распределенных случайных чисел?
4.Как программно моделируются дискретные случайные величины с бесконечным числом исходов?
5.В каком случае и каким образом реализуется совместное моделирование дискретной и непрерывной случайных величин?
6.Какова структура алгоритма моделирования гауссовского вектора с заданными корреляционными свойствами?
3.5. Задачи
Смоделировать последовательность из 500 случайных чисел с заданным законом распределения. Вычислить теоретически и экспериментально их математическое ожидание
идисперсию. Построить ряд распределения.
1.Распределение Пуассона
|
P k k exp |
k!, 0,4;1;8. |
|
2. |
Биномиальное распределение |
|
|
|
P k,n Cnkpk 1 p n k, |
p 0,4, n 4,20,100. |
|
3. |
Геометрическое распределение |
|
|
|
P k p 1 p k, k 0,1, , p 0,05,0,2. |
||
4. |
Гипергеометрическое распределение |
|
|
P m CMmCnN mM CnN , m 0,1, ,M; n 12, N 20, M 8. |
|||
5. |
Выполнить моделирование случайного события A, |
||
для которого P A p, p 0,01;0,1;0,5. Оценить |
вероятность |
||
события по выборке объема N 100,1000,10000. |
|
||
6. |
Разыграть 10 значений |
дискретной |
случайной |
61
величины X, закон распределения которой имеет следующий вид
|
|
X |
2 |
3 |
|
6 |
|
8 |
|
|
|
|
|
|
p |
0,1 |
0,3 |
|
0,5 |
|
0,1 |
|
|
|
|
|
7. Известно число событий, зарегистрированных в |
|||||||||||
течение последних 100 часов: |
|
|
|
|
|
|
|
|||||
|
Число событий в час |
4 |
5 |
6 |
|
7 |
8 |
|
|
|||
|
Частота (час.) |
|
5 |
11 |
16 |
|
23 |
45 |
|
|
||
Смоделировать регистрацию событий в течение 6 часов.
8.Смоделировать n 10 отсчетов гауссовского
случайного процесса x t с корреляционной |
функцией |
|||||
K 2 exp |
|
|
|
, взятых с шагом |
t 1 200 , |
при 2 4, |
|
|
|||||
0,1. |
|
|
||||
62
4. ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ
4.1. Выборочные моменты, расчет погрешностей
4.1.1. Общие соотношения
Набор значений x x1,x2, ,xn измеряемой величины
ξ, полученный при n-кратном повторении эксперимента, называется реализацией выборки. Можно считать, что все
возможные реализации |
составляют случайную выборку |
X X1, X2 , , Xn . Оценкой |
m m x параметра Θ называется |
некоторая статистика (функция выборки), приближенно соответствующая его истинному значению при конечном объеме выборки n ( m ) и сходящаяся к нему (в
вероятностном смысле) при неограниченном возрастании числа
выборок ( ). Случайная оценка |
|
m |
обычно |
m n |
|
|
характеризуется следующими числовыми значениями [1,16]: 1) средним значением оценки:
m  m
m u w u du;
u w u du;
2)смещением оценки: b m ;
3)дисперсией оценки:
D  m m 2
m m 2 u m 2 w u du
u m 2 w u du
или рассеянием оценки:
V  m 2
m 2 u 2w u du D b2 ;
u 2w u du D b2 ;
4) доверительной вероятностью P0 или доверительным интервалом Δ:
P P |
|
|
|
|
|
|
|
|
u du. |
|
|
|
m |
|
|
|
w |
|
|||
|
|
|||||||||
0 |
|
|
|
|
|
|
|
|||
63
Здесь w u – плотность вероятности оценки m .
4.1.2. Основные параметры и характеристики оценок
В дальнейшем будем считать, что выборка x подчиняется гауссовскому закону распределения, причем ее значения xi, xj, i,j 1,n являются некоррелированными (а,
следовательно, и статистически независимыми) при i j:
 xi
xi  xi
xi  xj
xj  xj
xj
 0.
0.
Тогда для наиболее часто используемых на практике параметров можно записать следующие соотношения.
Параметр m – математическое ожидание.
Оценка |
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
xi |
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Смещение оценки |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсия оценки |
2 n |
|
|
|
|
|
|
|
|
|
|
|||||
Распределение |
нормальное |
|
|
|
2 |
n |
|
|
||||||||
|
|
|
|
|
||||||||||||
оценки |
|
|
|
|
|
|
|
|
~ N |
, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доверительный |
|
|
z |
|
|
, где |
|
z |
|
|
1 1 P |
2 |
||||
|
p |
n |
|
p |
||||||||||||
интервал |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметр 2 – дисперсия:
а) математическое ожидание m известно
Оценка |
|
1 |
n |
|
|
s2 |
xi m |
2 |
|
|
n |
|||
|
|
i 1 |
|
|
|
|
|
|
|
Смещение оценки |
0 |
|
|
|
Дисперсия оценки |
2 4 |
n 2s4 n |
|
|
|
|
|
||
Распределение |
n2 |
(при n 100 – асимптотически |
||
оценки |
нормальное) |
|
||
64
|
|
Асимптотический |
zp |
|
|
, где zp 1 1 P0 2 |
||||||||||||
|
|
|
2 n |
|||||||||||||||
|
|
доверительный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интервал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) математическое |
ожидание неизвестно |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Оценка |
|
|
|
|
1 |
|
|
n |
|
|
|
|
||||
|
|
|
|
s2 |
|
|
xi |
x |
2 |
|
||||||||
|
|
|
|
n 1 |
||||||||||||||
|
|
|
|
|
|
i 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Смещение оценки |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Дисперсия оценки |
|
2 4 |
|
n 1 2s4 |
n 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Распределение |
|
n2 |
1 |
(при n 100 |
|
– асимптотически |
|
|||||||||
|
|
оценки |
|
нормальное) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||
Параметр mk – начальный момент k-го порядка |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Оценка |
|
~ |
|
|
1 |
n |
|
k |
|
|
|
|
||||
|
|
|
|
mk |
|
|
xi |
|
|
|
|
|||||||
|
|
|
|
|
n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Смещение оценки |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсия оценки |
|
m2k |
mk2 n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметр k – центральный момент k-го порядка
а) математическое ожидание m известно
Оценка |
|
~ |
|
1 |
n |
k |
|
|
|
k |
|
|
xi m |
|
|
|
n |
||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
Смещение |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсия |
2k |
n |
|
|
|
|
|
65

б) математическое ожидание неизвестно
|
Оценка |
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
k |
|
|
|
|
|
|
xi |
x |
k |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
n 1i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Смещение |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При n 1 |
оценки |
~ |
|
|
k для |
k 2,3,4 связаны |
||||||||||||||||||||||
|
|
mk и |
|||||||||||||||||||||||||||
соотношениями |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
||||||||||
|
2 m2 |
|
x |
|
, |
|
3 |
m3 |
3m2x 2 x , |
||||||||||||||||||||
|
|
~ |
|
|
|
|
~ |
|
|
|
|
~ |
|
|
2 |
|
|
|
|
4 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3 |
m4 |
4m3x 6m2 x 3 x . |
||||||||||||||||||||||||||
|
Параметр p – вероятность события |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка |
|
|
|
|
|
k |
, |
k – |
число |
положительных |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
исходов, n – число испытаний |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Смещение оценки |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Дисперсия оценки |
|
p 1 p |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Асимптотический |
|
zp |
|
|
|
|
|
|
, где |
|
||||||||||||||||||
|
|
|
p 1 p n |
||||||||||||||||||||||||||
|
доверительный |
|
|
zp 1 1 P0 2 |
|
|
|
|
|
|
|||||||||||||||||||
|
интервал |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2. Выборочные распределения
4.2.1. Общие соотношения
Теоретическими вероятностными характеристиками для непрерывной случайной величины ξ, полностью характеризующими ее в статистическом смысле, являются плотность вероятности w x и функция распределения
66
x
F x w u du.
Для дискретной случайной величины ξ такими характеристиками являются распределение вероятностей Pk P xk и функция распределения
F x |
xkPk . |
|
k:xk x |
При проведении эксперимента теоретическое распределение F x может быть:
а) частично известно с точностью до некоторых неизвестных параметров;
б) полностью неизвестным.
В первом случае экспериментальное определение w x , F x , Pk сводится к оценке параметров распределения,
|
|
|
|
2 |
|
~ |
|
которые находятся из выборочных моментов x, s |
, |
||||||
|
mk . |
||||||
Во втором случае производится непараметрическая |
|||||||
оценка распределения на основе |
|
|
|
||||
1) |
эмпирической функции распределения; |
|
|
|
|||
2) |
гистограммы; |
|
|
|
|||
3) |
полигона накопленных частот. |
|
|
|
|||
Эмпирической функцией распределения называется оценка F x по несгруппированной выборке. Гистограммой
называется оценка плотности вероятности w x по
сгруппированным данным.
Полигоном накопленных частот называется оценка функции распределения F x по сгруппированным данным.
Правило построения эмпирической функции распределения:
1) берется выборка x x1,x2, ,xn объемом n 100 и производится ее упорядочивание: x 1 x 2 x n .
67

2) строится функция
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
Fn u,x |
u x i , |
|
|
||||
|
|
|
|
|
|
|||||
где u 0 |
|
|
и u 1 |
|
|
ni 1 |
|
|
||
при u 0 |
при u 0 – функция Хевисайда. |
|||||||||
Для |
примера |
на рис. |
|
4.1 приведены |
теоретические |
|||||
(сплошными |
линиями) |
F |
u u и |
эмпирические |
||||||
|
|
|
|
|
|
|
|
|
|
|
(ступеньками) |
Fn u,x функции распределения стандартной |
|||||||||
гауссовской |
величины |
ξ. |
|
|
Эмпирические |
функции |
||||
распределения построены |
при |
|
n 200 (рис. 4.1а) |
и n 1000 |
||||||
(рис. 4.1б). Видно, что с ростом объема выборки n эмпирическая функция распределения сходится к теоретической.
Рис. 4.1
4.2.2. Правило построения гистограмм
1) Берется выборка x x1,x2, ,xn объемом n 100,
как правило, n ~ 2 20 102 .
2) Определяется число интервалов группировки r одним из возможных способов, например: r 0,55 1,25 n0,4 или r 4 5 lnn. При этом обычно число интервалов группировки
68

9 r 21. |
Если распределение предполагается симметричным, |
||||
то r целесообразно выбирать нечетным. |
aj,bj , |
|
|
|
|
3) |
Определяются длина x и границы |
j |
|
|
|
1,r |
|||||
интервалов группировки для всех xi:
x d r, |
d 1,02 xmax |
xmin |
, |
aj 1,02xmin j 1 x, |
bj 1,02xmin |
|
(4.1) |
j x. |
|||
Здесь xmin и xmax – минимальное и максимальное значение
выборки x. Для односторонних распределений (экспоненциального, релеевского, хи-квадрат и др.) полагается a1 0.
4) Подсчитывается количество kj элементов, попавших в интервал группировки aj,bj . При этом kj должно быть не менее 5 10. Если kj 5 10, то разбиение на интервалы
aj,bj необходимо произвести другим способом. |
|
5) Определяются относительные частоты |
|
j kj n или j kj n x |
(4.2) |
попадания значения случайной величины ξ в j-ый интервал и строится диаграмма столбцов высотой j или j, j 1,r.
В идеальном случае гистограмма меньше всего отличается от теоретической плотности вероятности в центре интервала группировки aj bj  2.
2.
Для примера на рис. 4.2 приведена теоретическая плотность вероятности (сплошной линией) w u стандартной
гауссовской случайной величины ξ и ее гистограмма (столбиками)
wg u j, |
aj u bj. |
(4.3) |
При построении гистограммы использовались объем выборки n 1000 и число интервалов r 10000,4 15.
69
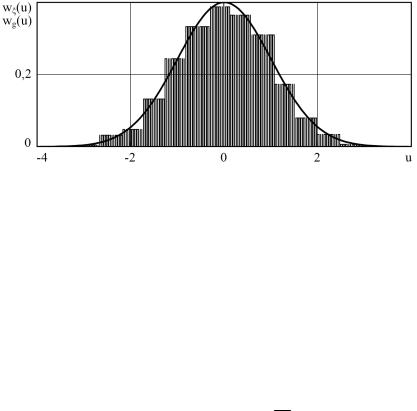
Рис. 4.2
4.2.3. Правило построения полигона накопленных
частот
Берется выборка x x1,x2, ,xn и определяется число
интервалов группировки так же, как и при построении гистограммы (пункты 1, 2, 3). Далее выполняются следующие действия:
4)подсчитывается количество Kq элементов выборки
x, попавших в интервал a1,a1 q x :
q
Kq kj , q 1,r ;
j 1
5) определяются выборочные вероятности
q
Fq Kq  n j
n j
j 1
и строится ступенчатая диаграмма, высота которой равна Fq на
интервале a0 q 1 x,a0 q x .
В идеальном случае полигон накопленных частот меньше всего отличается от теоретической функции распределения в конце интервала группировки.
Для примера на рис. 4.3 изображены теоретическая
функция распределения (сплошной линией) F u стандартной
70
