
2595
.pdf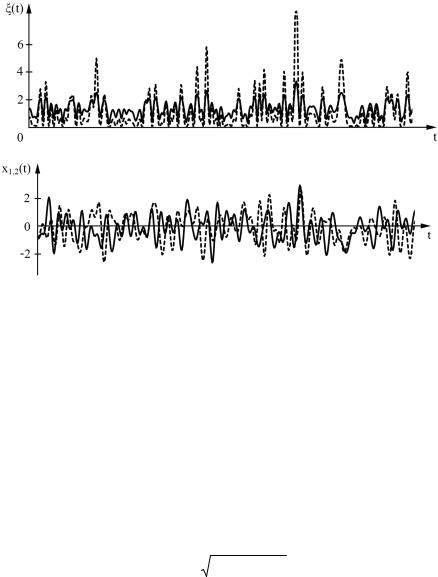
а)
б)
Рис. 7.3
7.4. Моделирование типовых негауссовских случайных процессов
Рассмотрим методы формирования типовых радиотехнических процессов с негауссовской статистикой, основанные на преобразовании гауссовских процессов.
Релеевский процесс
Одномерное распределение релеевского процесса имеет вид (2.5). Алгоритм формирования использует преобразование
|
t x2 t x2 t , |
|
|
где xi t , |
1 |
2 |
|
i 1,2 – независимые |
стандартные гауссовские |
||
случайные |
процессы с нулевыми |
математическими |
|
ожиданиями, |
|
|
|
|
131 |
|
|

единичными дисперсиями и корреляционными функциями
Rx  xi t xi t
xi t xi t  .
.
Первые моменты и корреляционная функция процесса
t равны
m |
2 |
, |
m 2 2 |
, |
D 2 2 , |
|
2 |
|
|
||
(7.16)
R 0,921Rx2 0,058Rx4 .
Для задач, не требующих высокой точности решения, в ряде (7.16) в силу его быстрой сходимости можно ограничиться первым членом разложения:
R 0,921Rx2 Rx2 .
Таким образом, формирование отсчета релеевского случайного процесса с корреляционной функцией R
сводится к формированию отсчетов двух независимых гауссовских случайных процессов с корреляционными функциями
Rx 
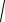 R . (7.17)
R . (7.17)
Пример 7.4. Пусть для моделирования задан релеевский случайный процесс, корреляционная функция которого может быть представлена в виде R exp 
 . Используя (7.17),
. Используя (7.17),
для корреляционных функций квадратур x1,2 t имеем:
Rx exp 
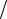 2 .
2 .
Используя готовый алгоритм (6.2) для моделирования гауссовского случайного процесса с экспоненциальной корреляционной функцией, получим следующий алгоритм для моделирования заданного релеевского случайного процесса:
j 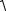
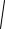

 1 2 1 j x1 j 1 2
1 2 1 j x1 j 1 2 
 1 2 2 j x2 j 1 2 ,
1 2 2 j x2 j 1 2 ,
где exp 0 t |
2 , |
1 j , |
2 j – последовательности |
независимых гауссовских чисел с параметрами ~ N 0,1 .
132
Процесс Релея-Райса (обобщенный релеевский процесс)
Распределение этого процесса описывается выражением
w y |
|
|
y |
|
|
A2 y2 |
|
Ay |
y 0, . |
|||||||||
|
|
|
|
exp |
|
|
|
I |
0 |
|
|
|
|
, |
||||
|
|
2 |
|
2 |
|
2 |
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Алгоритм |
|
|
моделирования |
|
|
осуществляется через |
||||||||||||
преобразование |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t |
|
|
|
, |
||||||||||||||
A x1 t 2 x2 t 2 |
z x1 t 2 x22 t |
|||||||||||||||||
где z A , |
а |
|
|
xi t , |
|
i 1,2 |
– |
|
независимые стандартные |
|||||||||
гауссовские случайные процессы с корреляционными
функциями Rx  xi t xi t
xi t xi t  .
.
Первые моменты и корреляционная функция процессаt связаны достаточно сложной зависимостью с параметрами
процессов x1 t и x2 t |
[10]. Однако для двух предельных |
|||||||
случаев эта связь упрощается: |
|
|
|
|||||
|
а) если z 1, то |
2 2 1 0,25z2 2, |
|
|
||||
m |
|
|
1 0,25z2 , D |
R Rx2 ; |
||||
|
2 |
|||||||
|
б) если z 3, то |
|
|
|
|
|||
|
|
|
|
|
R R |
. |
||
|
|
m A 1 1 2z2 |
, D 2 , |
|||||
|
|
|
|
|
x |
|
||
Процесс типа χn2
Такой процесс имеет одномерную плотность вероятности вида
w y |
|
|
|
1 |
|
|
n |
1 |
|
|
y |
|
|
, |
y 0, . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
y2 |
exp |
|
|
|
|
|||||
2 |
n 2 |
|
n |
n 2 |
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Процесс типа |
n2 |
по определению связан с n стандартными |
||||||||||||||
133

независимыми гауссовскими процессами xi t , |
i |
1,n |
с |
одинаковыми корреляционными функциями Rx  xi t xi t
xi t xi t 
соотношением
n
t n2 t 2 xi2 t .
i 1
При этом m n 2 , D 2n 4 , R Rx2 .
Квадратичная сумма величин с распределением Релея-Райса (нецентральное χn2 -распределение)
Рассмотрим случайный процесс вида
|
t 1 |
N |
x1i t zi 2 x22i t , |
|
||
|
2 |
(7.18) |
||||
|
|
i 1 |
|
|
|
|
где x1i t , |
x2i t , |
i |
|
– независимые |
стандартные |
|
1,n |
||||||
гауссовские процессы с одинаковыми корреляционными
функциями Rx |
x1i t x1i t x2i t x2i t . |
|||||
Одномерное распределение и первые два момента |
||||||
процесса (7.18) запишутся как |
|
|
|
|||
|
n 1 2 |
|
|
|
||
w y y |
In 1 2Z |
y , |
||||
Z2 |
exp y Z2 |
|||||
|
m |
Z2 n , |
|
|
|
|
|
D |
2Z2 n, |
|
|
|
|
n
где Z2 zi2 . Если же, кроме того, Z 3 5, то R Rx .
i 1
134

7.5. Контрольные вопросы
1.Назовите способы моделирования квазигармонических случайных процессов и условия целесообразности их применения.
2.Из каких соображений выбирается шаг дискретизации несущих гармоник и низкочастотных квадратур при моделировании квазигармонического процесса методом с квадратурными компонентами?
3.Какую интерполяционную формулу целесообразно применять при моделировании отсчетов квадратурных компонент квазигармонического процесса?
4.Как выглядит схема моделирования случайного процесса с произвольным законом распределения на основе гауссовского процесса? Каким образом могут быть найдены моменты и корреляционная функция моделируемого процесса?
5.В чем состоит суть трехэтапной схемы формирования негауссовского случайного процесса с заданным законом распределения?
6.В чем отличие модифицированного трехэтапного метода формирования негауссовского случайного процесса от стандартной трехэтапной схемы?
7.Каким образом может быть сформирован негауссовский случайный процесс с заданной корреляционной функцией?
8.Приведите алгоритмы формирования на ЭВМ типовых негауссовских случайных процессов.
7.6. Задачи
1.Сформировать узкополосный процесс с
корреляционной |
функцией |
R exp |
|
|
|
cos 0 , |
|
|
используя представление
R exp j 0 exp 
 j 0
j 0 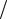 2.
2.
2. Сформировать узкополосный случайный процесс с
135

корреляционной функцией R exp 2 2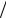 2 cos 0 .
2 cos 0 .
Примечание: |
использовать |
представление |
|
узкополосного случайного процесса x t |
в виде |
||
где X t , |
x t X t cos 0t Y t sin 0t , |
||
Y t – |
независимые квадратурные процессы с |
||
корреляционными функциями RX RY exp 2 2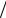 2 . 3. Сформировать узкополосный случайный процесс со
2 . 3. Сформировать узкополосный случайный процесс со
спектральной плотностью G 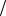 при 0
при 0 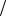 2.
2.
4. Сформировать узкополосный случайный процесс со спектральной плотностью
G G0 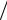 2 0 2 2 0 2
2 0 2 2 0 2
5.Сформировать равномерно распределенный процесс с корреляционной функцией R exp 

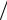 кор .
кор .
6.Сформировать релеевский процесс с корреляционной
функцией R exp 2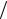 02 .
02 .
7. Сформировать обобщенный релеевский процесс (Релея-Райса) с корреляционной функцией квадратур
R exp 2

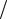 0 .
0 .
8.Сформировать релеевский процесс с корреляционной функцией R sin 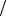 2 , 4.
2 , 4.
9.Сформировать хи-квадрат процесс с 6 степенями свободы и корреляционной функцией R exp 2 02 .
02 .
136
8. МОДЕЛИРОВАНИЕ ПУАССОНОВСКИХ
ПРОЦЕССОВ (СЛУЧАЙНЫХ ПОТОКОВ)
8.1. Моделирование пуассоновских процессов (случайных потоков)
8.1.1. Моделирование однородных пуассоновских случайных процессов
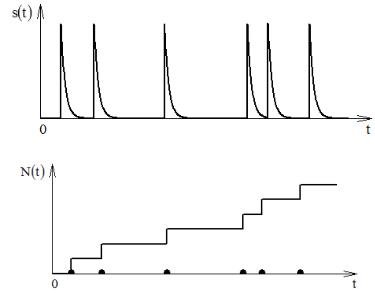
Дискретные (пуассоновские) случайные процессы могут возникать в самых различных приложениях физики, радиотехники, теории массового обслуживания и др. Одним из примеров может служить схема, приведенная на рис. 3.1. Здесь на выходе фотодетектора имеем последовательность импульсов (рис. 8.1а), которая преобразуется счетчиком в дискретный случайный процесс.
а)
б)
Рис. 8.1
137

Графическая иллюстрация дискретного случайного процесса показана на рис. 8.1б. Здесь точками показаны моменты появления событий (импульсов), а сплошной линией
– изменение числа событий с течением времени.
Другой пример (ядерная физика): пусть имеется источник ионизирующего излучения, частицы которого поступают на счетчик Гейгера, соединенного с пересчетным устройством (рис. 8.2). Тогда процесс на выходе пересчетного устройства также можно представить дискретным случайным процессом, аналогичным показанному на рис. 8.1б.
Рис. 8.2
Как видно из рис. 8.1б, дискретный случайный процесс представляет собой число событий из случайного потока, наступивших к моменту времени t, и может быть представлен двумя моделями:
1)последовательностью точек на оси времени (координатной оси, оси частот и т.д.), т.е. моментами времени появления событий из потока;
2)в виде ступенчатой функции N t непрерывного
времени.
Эти два описания во многом совпадают, но не во всех случаях являются эквивалентными.
Дискретный случайный процесс может обладать следующими свойствами.
Ординарность |
|
P N t t N t 1 t , |
(8.1) |
т.е. вероятность наступления более одного события на малом интервале t имеет более высокий порядок малости, чем t ;
138

Стационарность
Введем неперекрывающиеся интервалы на оси времени:
a1,b1 T1 , a2,b2 T2 |
, …, an,bn Tn и интервалы со сдвигом |
|
a1 ,b1 T1 , |
a2 ,b2 T2 , |
an ,bn Tn . |
Пуассоновский процесс называется стационарным, если его вероятностные свойства не изменяются при сдвиге во времени, т.е.
|
|
|
. (8.2) |
Pn k1,T1;k2,T2; ;kn,Tn Pn k1,T1;k2 |
,T2; ;kn |
,Tn |
Здесь ki , i 1,n – число точек (скачков) в i-ом интервале.
Для одномерной вероятности свойство стационарности пуассоновского процесса согласно (8.2) означает, что
P1 k,a,b P1 k,b a .
Независимость приращений
n |
|
Pn k1,T1;k2,T2; ;kn,Tn Pi ki,Ti , |
(8.3) |
i 1
т.е. процесс имеет независимые приращения значений на неперекрывающихся интервалах времени (отсутствие последействия).
Дискретный случайный процесс, удовлетворяющий свойствам (8.1)-(8.3), называется однородным пуассоновским процессом. Полное описание такого процесса достигается
заданием вероятностей P k,t Pk t появления k |
событий на |
интервале времени 0,t : |
|
Pk t t k exp t k!. |
(8.4) |
Здесь t – среднее число скачков процесса N t на интервале
0,t , λ – интенсивность пуассоновского потока (среднее число
точек в единицу времени).
Существует однозначное соответствие между значениями реализаций случайного процесса N t и
моментами наступления событий, образующих пуассоновский процесс. А именно: длительности интервалов τ между
139
соседними событиями, образующими пуассоновский процесс, есть независимые одинаково распределенные величины с экспоненциальной плотностью вероятности (2.8). При этом параметр λ будет иметь тот же самый смысл, что и в законе Пуассона. Таким образом, формируя случайную величину τ с экспоненциальным законом распределения, можно получить пуассоновский случайный процесс (и наоборот).
Если представляет интерес обрабатывать только каждую m-ую точку, то случайная величина
m
i ,
i 1
характеризующая длительность временного интервала между i- ой и i m -ой точками описывается законом распределения
Эрланга: |
m 1 |
|
|
|
w exp |
. |
(8.5) |
||
|
||||
m |
m 1 ! |
|
||
|
|
|||
При m 1 из (8.5) получаем экспоненциальный |
закон |
|||
распределения.
Для пуассоновских процессов имеют место следующие свойства:
1)свойство инвариантности к линейным
преобразованиям: |
сумма пуассоновских |
потоков si t с |
интенсивностями i |
представляет собой также пуассоновский |
|
поток с суммарной интенсивностью i |
; |
|
|
i |
|
2) свойство случайного прореживания точек: если текущая точка пуассоновского точечного потока интенсивности λ отбрасывается с вероятностью γ (оставляется
впотоке с вероятностью 1 ), то получающийся
разреженный поток также является пуассоновским с интенсивностью
1 . |
(8.6) |
140
