2551

58

Вычислив I 6 , из (3.19) найдем I5 , из (3.17) вычислим I4 , а затем из уравнений подстановки найдем токи I1 , I2 , I3 .

Как видно, аналитические вычисления достаточно громоздки, и для численных расчетов целесообразней использовать современные программные пакеты, например, MathCAD2001. Пример программы показан на рис. 3.3.

59

I1 2,75А, I2 1,366А, I3 1,384 А. Вычисленные значения

токов совпадают с полученными по приведенным выше формулам.

Общий метод расчета цепи по уравнениям Кирхгофа приводит к необходимости решения p линейных алгебраиче-

ских уравнений. При большом числе ветвей p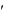 возникают ма-

тематические и вычислительные трудности. Это означает, что целесообразно искать методы расчета, требующие составления

ирешения меньшего числа уравнений.

3.4.Метод контурных токов

Метод контурных токов базируется на уравнениях второго закона Кирхгофа и приводит к необходимости решения p q 1 уравнений, p - число всех ветвей, в том числе и содержащих идеальные источники тока.

В цепи выбираются p q 1 независимых контуров и для каждого k -го из них вводится кольцевой (замкнутый) контурный ток Ikk (двойная индексация позволяет отличать кон-

турные токи от токов ветвей). Через контурные токи можно выразить все токи ветвей и для каждого независимого контура записать уравнения второго закона Кирхгофа. Система уравнений содержит p q 1 уравнений, из которых определяются

все контурные токи. По найденным контурным токам находятся токи или напряжения ветвей (элементов).

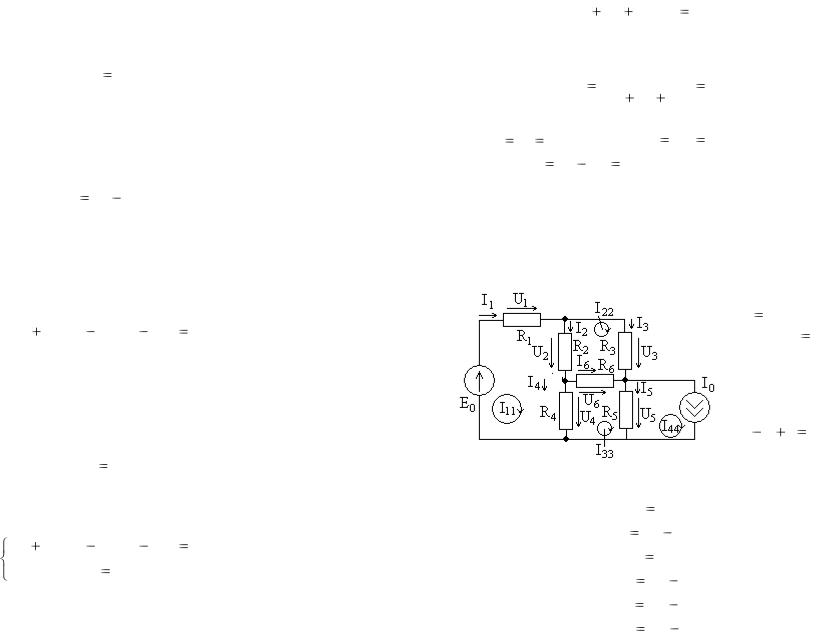
кает только контурный ток I22 и его направление совпадает с I1 , поэтому ток ветви I1 равен

Для контуров, не содержащих идеальные источники тока, составляем уравнения второго закона Кирхгофа с использованием закона Ома, в данном примере записывается одно уравнение

Если в контур включен идеальный источник тока, то для него уравнение второго закона Кирхгофа не составляется, а его контурный ток равен току источника с учетом их положительных направлений, в рассматриваемом случае

Тогда система уравнений принимает вид

В результате подстановки второго уравнения в первое получим

61

ветственно I2 I11 I22 0,714А, что полностью совпадает с

полученными ранее результатами. При необходимости по найденным значениям токов ветвей по закону Ома можно вычислить напряжения на элементах цепи.

Рассмотрим более сложный пример цепи на рис. 3.2, схема которой с заданными контурными токами показана на рис. 3.4. В этом случае число ветвей p 7 , количество

Первые три контура не содержат идеальных источников тока, тогда с учетом (3.28) и использованием закона Ома для них можно записать уравнения второго закона Кирхгофа,

В четвертом контуре присутствует идеальный источник тока, поэтому для него уравнение второго закона Кирхгофа не составляется, а контурный ток равен току источника (они совпадают по направлению),

Подставляя (3.30) в систему (3.29), после преобразования получим три уравнения для контурных токов в виде

Систему уравнений (3.31) можно решить аналитически (например, методом подстановки – проделайте это), получив формулы для контурных токов, а затем из (3.28) определить токи ветвей. Для численных расчетов удобно использовать пакет программ MathCAD, пример программы показан на рис. 3.5. Результаты вычислений совпадают с расчетами, приведенными на рис. 3.3.

Как видно, метод контурных токов требует составления и решения меньшего числа уравнений по сравнению с общим методом расчета по уравнениям Кирхгофа.

63

Рис. 3.5

3.5. Метод узловых напряжений

Метод узловых напряжений базируется на первом за-

коне Кирхгофа, при этом число уравнений равно q 1.

В цепи выделяются все q узлов и один из них выбирается в качестве базисного, которому присваивается нулевой потенциал. Потенциалы (напряжения) U11,U22 … U(q 1)( q 1) остальных q 1 узлов отсчитываются от базисного, их положи-

тельные направления обычно выбираются стрелкой в базисный узел. Через узловые напряжения с использованием закона Ома и первого закона Кирхгофа выражаются токи всех ветвей

64

и для q 1 узлов записываются уравнения первого закона

Кирхгофа.

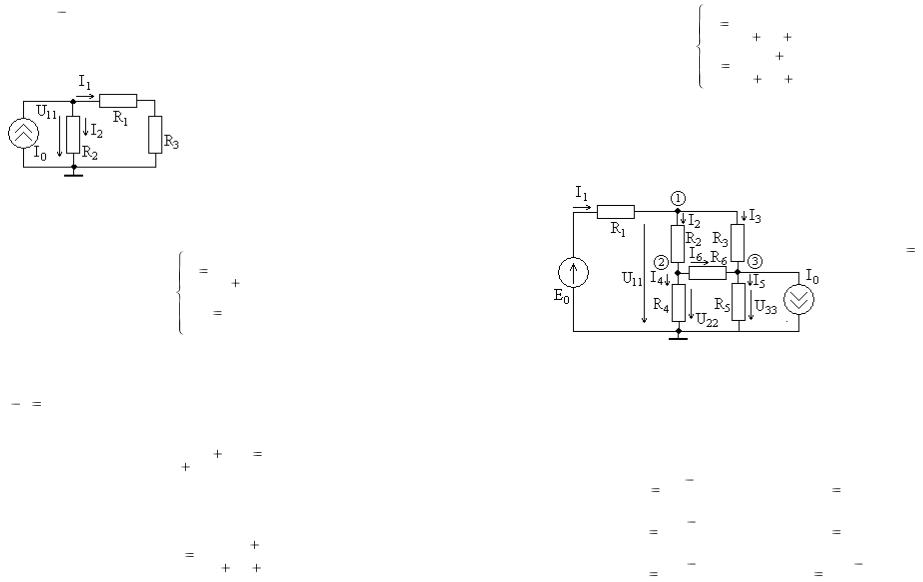
Рассмотрим пример цепи, показанной на рис. 3.1, для метода узловых напряжений ее схема показана на рис. 3.6. Нижний узел обозначен как базисный (для этого используется символ «земля» - точка нулевого потенциала), напряжение верхнего узла относительно базисного обо-

Рис. 3.6 значено как U11 . Выразим через него токи ветвей

По первому закону Кирхгофа с учетом (3.32) запишем единственное уравнение метода узловых напряжений

( q 1 1),

Решая уравнение, получим

а из (3.32) определим токи ветвей

65

Полученные результаты совпадают с полученными рассмотренными ранее методами.

Рассмотрим более сложный пример цепи, показанной на рис. 3.2 при тех же исходных данных, ее схема показана на рис. 3.7. В цепи q 4 узла,

нижний выбран базисным, а три остальные обозначены номерами в кружках. Введены

Рис. 3.7. положительные направления и обо-

значения узловых напряжений U11 , U22 и U 33 .

По Закону Ома с использованием второго закона Кирхгофа определим токи ветвей,

По первому закону Кирхгофа для узлов с номерами 1, 2 и 3 необходимо составить три уравнения,

I1 I2 I3 0,

I3 I6 I5 I0 .

Подставляя (3.36) в (3.37), получим систему уравнений метода узловых напряжений,

После преобразования и приведения подобных получим

Программа расчета узловых напряжений и токов ветвей приведена на рис. 3.8. Как видно, полученные результаты совпадают с полученными ранее другими методами расчета.

Проведите аналитический расчет узловых напряжений, получите формулы для токов ветвей и вычислите их значения.

67

Рис. 3.8

3.6. Метод наложения

Метод наложения заключается в следующем.

Реакция цепи (ток или напряжение) на воздействие нескольких источников равна сумме реакций на действие каждого из них в отдельности, при этом остальные источники должны быть выключены

68

Выключение идеальных источников означает замену:

-идеального источника напряжения коротким замыканием, так как его внутреннее сопротивление равно нулю;

-идеального источника тока холостым ходом (разрывом цепи) так как его внутреннее сопротивление

стремится к бесконечности.

Расчет проводится следующим образом. В цепи, содержащей несколько источников, поочередно выбирается каждый из них, а остальные отключаются. При этом образуются цепи с одним источником, число которых равно количеству источников в исходной цепи. В каждой из них проводится расчет искомого сигнала, а результирующий сигнал определяется их суммой.

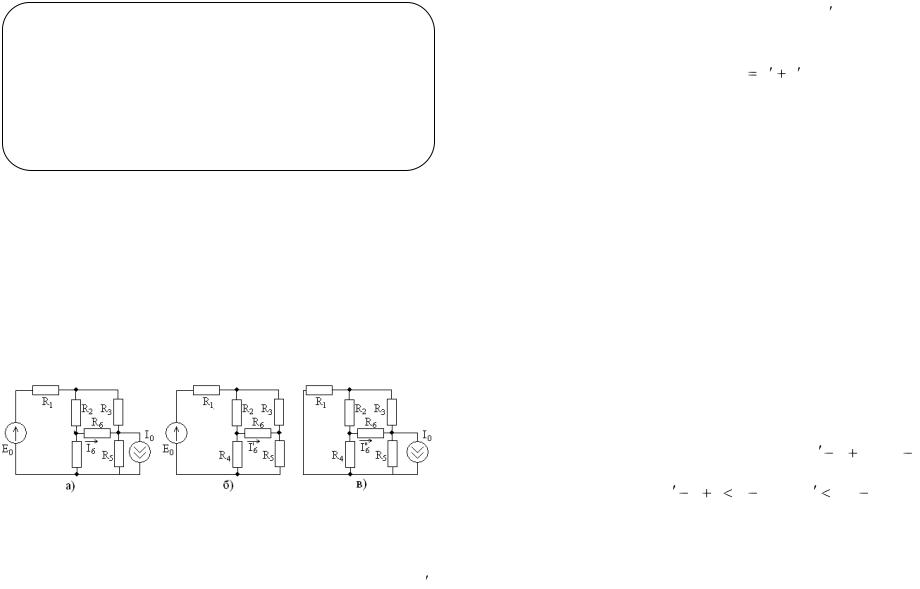
В качестве примера рассмотрим расчет тока I6 в цепи, показанной на рис. 3.2, ее схема показана на рис. 3.9а.

Рис. 3.9.

При выключении идеального источника тока (его цепь разрывается) получается цепь, показанная на рис. 3.9б, в которой любым из рассмотренных методов определяется ток I6 .

Затем выключается идеальный источник напряжения (он заменяется коротким замыканием) и получается цепь, показанная

69

на рис. 3.9а, в которой находится ток I6. Искомый ток I6 равен

I6 I6 I6.

Проведите аналитические и численные расчеты самостоятельно, сравните с полученными ранее результатами, на-

пример, (3.20).

3.7. Сравнительный анализ методов расчета

Метод расчета, основанный на законе Ома, пригоден для расчета сравнительно простых цепей с одним источником. Его нельзя использовать для анализа цепей сложной структуры, например, мостового типа вида рис.3.9.

Общий метод расчета цепи на основе уравнений законов Ома и Кирхгофа универсален, но требует составления и решения системы из 2 p уравнений, которая легко преобразу-

ется в систему из p уравнений. При большом числе ветвей

резко возрастают вычислительные затраты, особенно при необходимости аналитических расчетов.

Методы контурных токов и узловых напряжений более эффективны, так как приводят к системам с меньшим числом

метод контурных токов эффективнее, а иначе целесообразно применять метод узловых напряжений.

Метод наложения удобен, когда при отключении источников происходит резкое упрощение цепи.

В системах схемотехнического моделирования цепей, например, MicroCAP или OrCAD в основном применяют метод узловых напряжений

3.8. Задания для самостоятельного решения

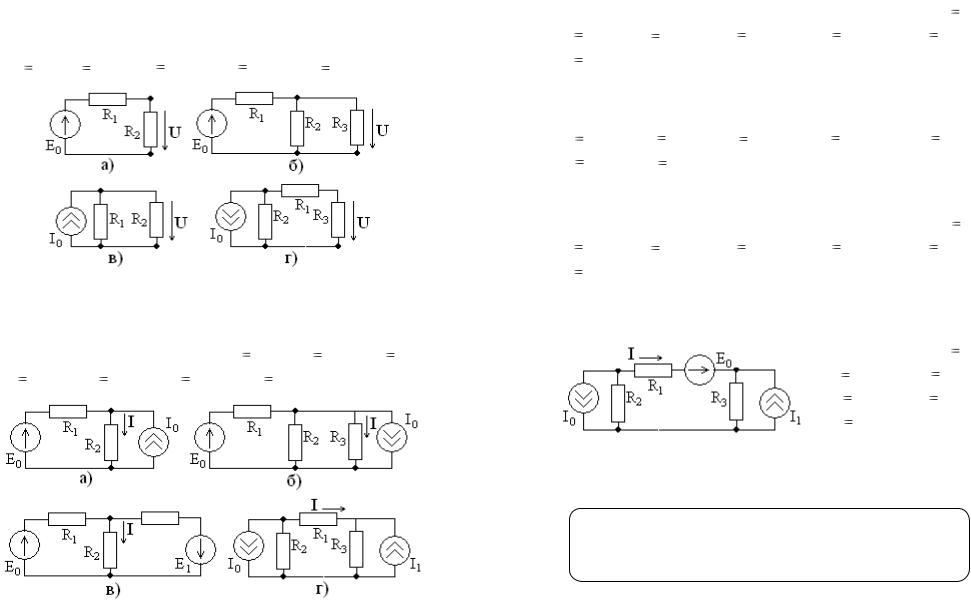
Задание 3.1 С помощью закона Ома определите напряжение U в цепях, схемы которых показаны на рис. 3.10 при E0 1В, I0 5 мА, R1 1 кОм, R2 5 кОм, R3 10 кОм.

Рис. 3.19

Задание 3.2 Общим методом расчета на основе законов

Рис. 3.11

71

Проведите сравнительный анализ эффективности рассмотренных методов расчета цепей постоянного тока

72

4.ГАРМОНИЧЕСКИЕ ТОКИ И НАПРЯЖЕНИЯ

ВЛИНЕЙНЫХ ЦЕПЯХ

4.1. Гармонические ток и напряжение в элементах цепи

В элементах цепи R, L, и C взаимосвязь мгновенных значений тока и напряжения определяется законом Ома, необходимые соотношения приведены в табл. 1.1.

Рассмотрим гармонические ток и напряжение на элементе Э (рис. 4.1) в виде

Рис. 4.1

Рассмотрим сопротивление R, для которого можно за-

писать

Сравнивая полученный результат с выражением для напряжения из (4.1), получим выражение закона Ома для амплитуд тока и напряжения.

и соотношение для начальных фаз

Как видно из (4.3), амплитуды (и действующие значения) гармонических тока и напряжения в сопротивлении связаны законом Ома в классической формулировке прямой пропорциональности.

73

лении одинаковы, сдвиг фаз 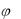между напряжением и током равен нулю,

Мгновенная мощность (1.6) гармонических сигналов в сопротивлении равна

положительна, то есть сопротивление только потребляет мощность от источника сигнала. Это гармоническая функция времени с периодом

Рис. 4.2 повторения в два раза меньше периода сигнала.

Средняя мощность (1.8) гармонических сигналов в сопротивлении определяется выражением

где I Д иU Д - действующие значения тока и напряжения,

Это значение показано пунктирной линией на временной диаграмме рис. 4.2.

В емкости C мгновенные значения тока и напряжения связаны соотношением (табл.1.1)

После преобразования тригонометрической функции к канонической форме гармонического сигнала получим

где xC - модуль реактивного сопротивления емкости (Ом), а bC - реактивная проводимость емкости (Сим=1/Ом).

Позднее увидим, что реактивное сопротивление емкости отрицательно.

Из (4.11) получим уравнения связи амплитуд (и действующих значений) гармонического тока и напряжения в емкости

75

которые представляют собой выражение закона Ома для емкости в классической формулировке прямой пропорциональности.

Из (4.12) следует, что гармонический ток в емкости опережает по фазе приложенное к ней напряжение (напряжение отстает по фазе от тока) на угол / 2 радиан или 900. Сдвиг фаз между напряжением и током в емкости равен

u i 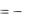/ 2 . (4.16)

На рис. 4.3 показаны временные диаграммы тока и напряжения в емкости. Ток i(t) опережает

по фазе напряжение на 900, что отражается на временной диаграмме сме-

Рис. 4.3 щением кривой тока влево на четверть периода.

Мгновенная мощность в емкости из (4.1) и (4.9) равна

а после тригонометрических преобразований получим

Временная диаграмма мгновенной мощности показана на рис. 4.4

76

Мгновенная мощность электрических сигналов в емкости может быть положительной (емкость накапливает энергию электрического поля) и отрицательной (емкость отдает во внешнюю цепь ранее накопленную энергию). Средняя мощность гармонических сигналов в емкости равна нулю, то

Рис. 4.4. есть емкость не потребляет мощность от гармонического источника.

Для индуктивности L мгновенные значения тока и напряжения связаны соотношением закона Ома из табл.1.1, тогда с учетом выражения для тока из (4.1) получим

а после преобразований

Сравнивая (4.18) с выражением для напряжения (4.1), получим уравнения связи для амплитуд (действующих значений) тока и напряжения

и их начальных фаз

Введем обозначения

77

где xL - реактивное сопротивление индуктивности (Ом), а bC - модуль реактивной проводимости индуктивности

(Сим=1/Ом). Позднее увидим, что реактивная проводимость индуктивности отрицательна.

Тогда получим выражения закона Ома для амплитуд (действующих значений) тока и напряжения в индуктивности

Согласно (4.20) гармонический ток в индуктивности отстает по фазе от напряжения (напряжение опережает по фазе тока) на угол / 2 радиан или 900. Сдвиг фаз между напряжением и током в индуктивности равен

u i 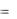/ 2 . (4.24)

Временные диаграммы тока и напряжения в индуктивности показаны на рис. 4.5. В отличие от аналогичных графиков для емкости на рис. 4.3 ток и напряжение меняются

Рис. 4.5. местами, кривая напряжения смещена вправо относительно тока на четверть периода, что соответствует опере-

жению по фазе на 900.

78