
2551
.pdf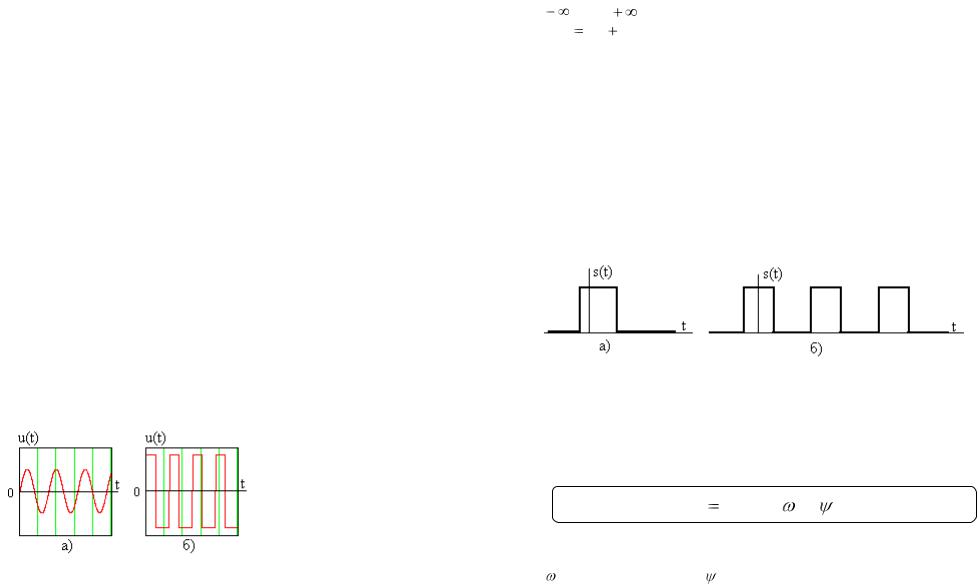
38
2. ЭЛЕКТРИЧЕСКИЕ СИГНАЛЫ
2.1. Информационные сигналы
В информационных системах сигнал является материальным носителем информации. В качестве сигналов могут использоваться различные физические процессы, например, звуковые колебания, световые импульсы, намагниченность ленты в магнитофоне, электромагнитные волны и т.д. В электротехнике в качестве сигналов используются изменяющиеся во времени токи или напряжения.
Сигналы можно разделить на детерминированные и случайные. Детерминированными называют сигналы, для которых заранее известны вид функции времени и ее параметры. Для случайных сигналов либо функция времени, либо ее параметры неизвестны и могут принимать случайные значения, известны лишь распределения их вероятностей. Строго говоря, информационные сигналы всегда являются случайными функциями времени. Их анализ выходит за рамки изучаемого курса.
Детерминированные сигналы различной формы широко используются, например, как управляющие воздействия в различных электронных системах и устройствах, при измерении их характеристик. Промышленность выпускает формирователи (генераторы) таких сигналов и измерители их параметров. В частном случае в качестве сигналов рассматриваются постоянные (не меняющиеся во времени) токи и напряжения.
Примеры временных диаграмм сигналов (гармонического и последовательности прямоугольных импульсов) показаны на рис. 2.1.
Рис. 2.1
39
Переменные (меняющиеся во времени) сигналы делятся на периодические и непериодические. Периодические сигналы
повторяются через промежуток времени T |
на интервале от |
||
до |
, математически это можно |
записать в |
виде |
s(t) s(t |
kT) , где k - любое целое число. Величину T |
назы- |
|
вают периодом сигнала, который измеряется в единицах времени. Примером являются сигналы, показанные на рис. 1.39.
Непериодические сигналы не повторяются во времени. Это могут быть случайные процессы (например, речевой сигнал с выхода микрофона), или одиночные импульсы. Одиночный импульсный сигнал появляется на ограниченном интервале времени, ни до этого, ни после сигнал не возникает. Примером может служить одиночный импульс (рис. 2.2а) или пачка импульсов (рис.2.2б), их форма может быть разнообразной. Одиночные сигналы можно рассматривать как периодические с бесконечно большим периодом.
Рис. 2.2
2.2. Гармонический сигнал
Гармонический сигнал s(t) традиционно записывают в
виде
s(t) Sm cos( t 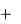 ) , (2.1)
) , (2.1)
где Sm - амплитуда сигнала (индекс m от слова «максимум»), - круговая частота, а - начальная фаза.
40
Временная диаграмма гармонического сигнала s(t) показана на рис. 2.3.
Рис. 2.3.
Амплитуда гармонического сигнала – это его максимальное значение, она измеряется в единицах сигнала (вольтах
для напряжения и амперах для тока). |
|
||
Период T определяет циклическую частоту f |
повто- |
||
рения сигнала, |
|
|
|
f |
1 |
, |
(2.2) |
|
|||
|
T |
|
|
измеряемую в герцах (Гц). Ее физический смысл – число периодов колебаний в секунду.
Аргумент косинуса в (2.1) вида
(t) |
t |
(2.3) |
называют полной фазой колебания, она пропорциональна текущему времени и измеряется в радианах или градусах.
Круговая частота 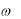 равна
равна
2 |
2 f |
(2.4) |
|
|
|||
T |
|||
|
|
41
и представляет собой число радиан, на которое изменяется
полная фаза колебания в единицу времени (1 с). |
|
|
При t 0 полная фаза равна (0) |
, |
поэтому пара- |
метр 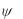 называют начальной фазой гармонического сигнала. Она измеряется в радианах или градусах. Так как период функции cos( ) равен 2
называют начальной фазой гармонического сигнала. Она измеряется в радианах или градусах. Так как период функции cos( ) равен 2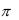 или 3600, то начальная фаза оказы-
или 3600, то начальная фаза оказы-
вается многозначной величиной. Например, значения началь-
ной фазы 300 и (300+3600)=3900, а также (300-3600)=-3300 ока-
зываются эквивалентными. В общем случае можно записать 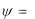
 k
k  3600 или
3600 или 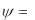
 k
k  2 , где k - целое число. Для
2 , где k - целое число. Для
устранения неоднозначности договариваются, что значения начальной фазы должны находиться, например, в интервале от
0 до 2 , или от |
|
до |
(аналогичные границы могут быть |
|||||||||||||||
заданы в градусах). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
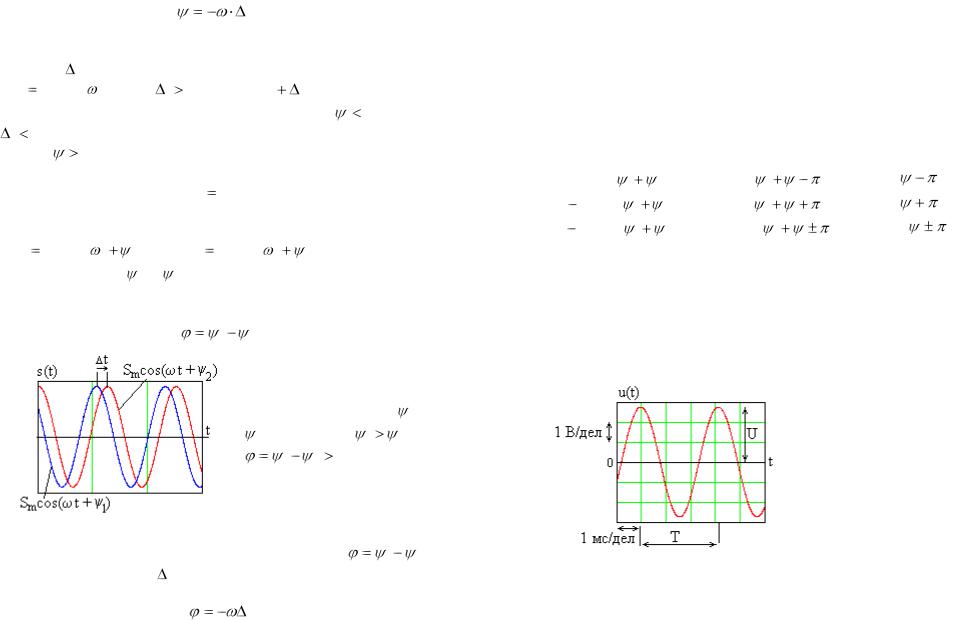
Начальная фаза связана со смещением гармонического |
|||||||||||||||||
сигнала во времени на величину |
|
t относительно функции |
||||||||||||||||
s(t) |
Sm cos( t) , как показано на рис. 2.3. Функция s(t |
|
t |
|
) |
|||||||||||||
|
|
|||||||||||||||||
смещена влево относительно s(t) , |
а s(t |
|
t |
|
) - вправо. Поло- |
|||||||||||||
|
|
|||||||||||||||||
жительные значения |
t отсчитываются в сторону увеличения |
|||||||||||||||||
t , а отрицательные – наоборот. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Из (2.1) можно записать |
|
|
|
|
|
|
|
|
|
|
|
||||||
s(t) |
Sm cos( t |
) |
Sm cos |
t |
|
|
|
Sm cos (t |
t) , (2.5) |
|||||||||
|
|
|
||||||||||||||||
где смещение во времени |
t |
равно |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
t |
|
|
|
. |
|
|
|
|
|
|
(2.6) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда для начальной фазы получим |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
42 |
|
|
t . |
(2.7) |
Как видно, начальная фаза определяется временным |
||
сдвигом t |
гармонического сигнала относительно функции |
|
s(t) Sm cos( |
t) . При t 0 сигнал s(t t) смещается впра- |
|
во по оси времени, при этом начальная фаза |
0 , а если |
|
t 0 , то временная диаграмма смещается влево по оси вре-
мени, а |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
Величина начальной фазы зависит от начала отсчета |
|||||||||||||
времени (положения точки t |
0 ). При смещении начала от- |
||||||||||||
счета времени изменяется и начальная фаза. |
|
|
|
|
|
||||||||
Применительно |
к |
двум |
гармоническим |
сигналам |
|||||||||
s1 (t) Sm cos( t |
1 ) |
и |
s2 (t) |
Sm cos( t |
|
2 ) |
с разными на- |
||||||
чальными фазами |
1 |
и |
2 |
вводится в рассмотрение сдвиг фаз |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
между первым и вторым сигналами, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
2 . |
|
|
|
|
(2.8) |
|
|
|
|
|
|
|
|
На рис. 2.4 показаны два |
||||||
|
|
|
|
|
|
|
гармонических |
сигнала |
с |
||||
|
|
|
|
|
|
|
начальными |
фазами |
1 |
и |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 , |
причем |
1 |
2 |
и |
||
|
|
|
|
|
|
|
|
1 |
2 |
0 . |
В |
этом |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
случае говорят, что первый |
||||||
|
|
|
|
|
|
|
сигнал опережает по фазе |
||||||
|
|
|
|
|
|
|
второй или второй сигнал |
||||||
|
Рис. 2.4 |
|
|
|
|
отстает по фазе от перво- |
|||||||
|
|
|
|
|
|
|
го. Сдвиг фаз |
1 |
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
связан со смещением |
t |
сигналов во времени, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
t , |
|
|
|
|
(2.9) |
|
43
положительные значения временного сдвига отсчитываются в направлении оси времени. Гармоническое колебание может быть задано в нетипичной форме, которую необходимо преобразовать к виду (2.1), иначе начальная фаза оказывается неопределенной. Примеры преобразования показаны в табл. 2.1.
Таблица 2.1.
Исходный сиг- |
Преобразованный сигнал |
Начальная |
||||
нал |
|
|
|
|
фаза |
|
Sm sin( |
t |
) |
Sm cos( |
t |
/ 2) |
/ 2 |
|
|
|
|
|
|
|
Sm sin( |
t |
) |
Sm cos( |
t |
/ 2) |
/ 2 |
|
|
|
|
|
|
|
Sm cos( |
t |
) |
Sm cos( t |
) |
|
|
|
|
|
|
|
|
|
2.3. Измерение параметров гармонического сигнала с помощью электронного осциллографа
Параметры гармонического сигнала можно определить экспериментально с помощью электронного осциллографа. На рис. 2.5 показан пример наблюдаемой на экране осциллограммы, на которой отображается временная диаграмма наблюдаемого сигнала и задана координатная сетка.
Шаг сетки по вертикали равен 1 В на деление, а амплитуда составляет 2,7 деления, следовательно, ее величина равна U=2,7 В. По горизонтали на оси времени шаг сетки 1 мс на
Рис. 2.5 одно деление, период сигнала равен 3,1 деления, то есть T=3,1 мс. При измеренном периоде нетрудно определить
циклическую частоту сигнала

|
|
|
|
|
|
|
44 |
|
|
|
|
||
|
f |
1 |
|
|
1 |
|
323 |
Гц |
|||||
|
|
|
|
|
|
|
|
||||||
T |
3,1 |
10 3 |
|||||||||||
|
|
|
|
|
|
||||||||
и круговую частоту |
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
2 |
|
|
2,03 103 |
рад/с. |
|||||
|
|
|
|
|
|
|
|
|
|||||
|
T |
3,1 10 |
3 |
|
|||||||||
|
|
|
|
|
|
||||||||
При определении |
амплитуды необходимо устанавли- |
||||||||||||
вать нулевой уровень напряжения. Удобнее измерять расстояние по вертикали между максимальным и минимальным значениями сигнала, которое называют размахом. Для гармонического сигнала размах равен удвоенной амплитуде.
Начальная фаза сигнала может быть определена только при условии задания начала отсчета времени – точки t 0 . Однако это начало отсчета условно (может быть задано в любой момент времени), поэтому осциллографическое измерение начальной фазы гармонического сигнала практически не имеет смысла.
Совершенно иная ситуация возникает при измерении сдвига фаз между двумя гармоническими сигналами с одинаковой частотой. При этом на экране осциллографа должны наблюдаться две временных диаграммы измеряемых гармониче-
|
ских |
напряжений, |
как |
|
|
показано на рис. 2.6. |
|||
|
Взаимное смещение |
t |
||
|
сигналов на экране ос- |
|||
|
циллографа |
не зависит |
||
|
от начала отсчета вре- |
|||
|
мени. |
Это |
позволяет |
|
|
экспериментально |
оп- |
||
|
ределить фазовый сдвиг |
|||
|
одного сигнала отно- |
|||
Рис.2.6 |
сительно другого, кото- |
|||
|
|
45 |
|
|
|
рый выбран в качестве опорного. |
|
|
|
||
Если необходимо определить |
сдвиг |
фаз |
напряжения |
||
u1 (t) Um1 cos( t |
1 ) |
относительно |
выбранного |
в качестве |
|
опорного напряжения |
u2 (t) Um2 cos( t |
2 ) , то по времен- |
|||
ной диаграмме рис. 2.6 получим, что смещение во времени сигнала u1(t) равно t  0.5 деления или t
0.5 деления или t 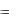 1 мкс (знак
1 мкс (знак
минус означает, что сигнал смещен относительно опорного влево, то есть раньше во времени).
Период T гармонических колебаний на рис. 2.6 равен
6,28 мкс, а круговая частота соответственно |
|
|
|||||||||
|
|
2 |
|
2 |
1 106 рад/с, |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
T |
6,28 10 6 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
тогда |
из |
(2.9) |
|
получим |
величину |
сдвига |
фаз |
||||
1 |
2 |
t 1 |
рад. Как видно, напряжение u1(t) опе- |
||||||||
режает по фазе опорное напряжение u |
2 |
(t) на 1 рад или 570. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Если в качестве опорного напряжения выбрать u1(t) , то временной сдвиг от него второго сигнала u2 (t) будет равен
t 1мкс, а сдвиг фаз |
2 |
1 |
1 рад или -570. Это озна- |
|
|
чает, что напряжение u2 (t) отстает по фазе от u1(t) на 1 рад. Временной сдвиг напряжения u1(t) относительно u2 (t)
на рис. 2.6 можно оценивать и так, как показано на рис. 2.7,
при этом |
t 2,64 деления или 5,28 мкс. При этом новое зна- |
||||
чение t |
оказывается больше полученного ранее на величину |
||||
периода T , а сдвиг фаз равен |
1 |
2 |
t |
5,28 рад. |
|
|
|
|
|
||
В результате оказывается, что напряжение u1(t) отстает |
|||||
по фазе от опорного сигнала u2 (t) |
на угол 5,28 рад, что экви- |
||||
валентно полученному ранее результату, так как отличается от него на величину 2 .
46
Для обеспечения однозначности фазового сдвига его величину обычно выбирают в интервале от  до
до  или
или
3600 .
Рис. 2.7
2.4. Последовательность прямоугольных импульсов
В электронной технике широкое распространение получили последовательности импульсов прямоугольной формы. На рис.2.8 показаны примеры однополярных (рис. 2.8а) и двухполярных (рис. 2.8б) прямоугольных импульсов.
Рис. 2.8
Сигнал в виде последовательности прямоугольных импульсов характеризуется тремя основными параметрами:
амплитудой Sm , измеряемой в вольтах или амперах;
длительностью 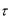 ; периодом повторения T .
; периодом повторения T .
47
На практике часто используется частота повторения импульсов f 1/T , измеряемая в герцах (Гц).
Переход сигнала от нижнего уровня к верхнему называют фронтом, а от верхнего уровня к нижнему – срезом.
|
|
У |
прямо- |
|
|
угольных |
импуль- |
||
|
сов |
длительности |
||
|
фронта |
tФР и сре- |
||
|
за |
tСР равны |
ну- |
|
|
лю. На практике их |
|||
|
длительность |
ко- |
||
|
нечна, как показа- |
|||
Рис. 2.9 |
но на рис. 2.9. |
|
||
2.5. Числовые характеристики (значения) сигналов
Детерминированный периодический сигнал s(t) - ток i(t) или напряжение u(t) - полностью описывается соответствующей функцией времени. Значения s(t) называют мгновенными. Например, мгновенные значения гармонического тока i(t) 5cos(106 t 300 ) мА.
В инженерной практике широко используются различные его числовые характеристики.
Частота повторения (циклическая) f 1/T , измеряет-
ся в герцах.
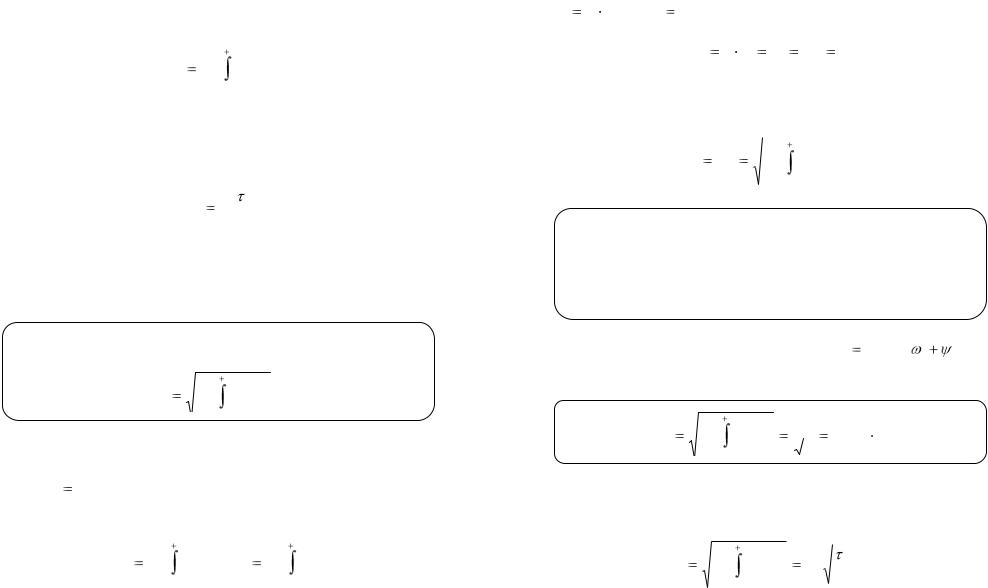
Амплитуда (измеряется в единицах сигнала - вольтах или амперах):
 для гармонического сигнала – его максимальное значение или половина размаха (разности между максимальным и минимальным значениями;
для гармонического сигнала – его максимальное значение или половина размаха (разности между максимальным и минимальным значениями;  для импульсного сигнала амплитуда обычно определя-
для импульсного сигнала амплитуда обычно определя-
ется как разность между максимальным и минимальным значениями (амплитуда равна размаху).
48
Среднее значение (постоянная составляющая) сиг-
нала SСР определяется выражением
|
1 t 0 T |
(2.10) |
||
SСР |
|
s(t)dt. |
||
T |
||||
|
t 0 |
|
||
Для гармонического сигнала среднее значение равно нулю и не является информативным, а для последовательности прямоугольных импульсов, показанных на рис. 2.8а, из (2.10) получим
SСР |
S m |
. |
(2.11) |
|
T |
||||
|
|
|
Среднее значение сигнала характеризует постоянную компоненту, которая может присутствовать в произвольном переменном сигнале.
Действующее значение сигнала равно
|
|
1 t 0 |
T |
|
||
S |
Д |
|
|
s2 (t)dt. |
(2.12) |
|
T |
||||||
|
|
|
||||
|
|
|
|
|||
Оно определяется из энергетических соображений. Если сопротивление цепи активно и равно R=1 Ом, то напряжение u(t) Ri(t) равно току i(t) , а средняя мощность PСР периодического сигнала согласно (1.8) определяется выражением
|
1 t 0 T |
1 t 0 T |
|
||
P |
|
Ri(t)u(t)dt |
|
s2 (t)dt , |
(2.13) |
|
|
||||
СР |
T |
|
T t 0 |
|
|
|
t 0 |
|
|||
то есть соответствует среднему квадрату сигнала.
|
|
|
|
49 |
|
|
|
||
|
Согласно (1.9) |
для постоянных тока I |
и напряжения |
||||||
U |
R I при R 1 Ом мощность P равна |
|
|||||||
|
P |
I U I 2 |
U 2 S2 , |
(2.14) |
|||||
где |
S - значение тока или напряжения. Приравнивая (2.13) и |
||||||||
(2.14), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 0 |
T |
|
||
|
S |
S |
Д |
|
|
|
s2 (t)dt . |
(2.15) |
|
|
|
T t 0 |
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Из (2.15) следует, что действующее значение переменного сигнала – это такое эквивалентное значение постоянного тока или напряжения, которое выделяет в нагрузке (сопротивлении R ) ту же мощность, что и исходный переменный сигнал.
Для гармонического сигнала s(t) Sm cos( t |
) из |
(2.15) получим
|
|
1 t 0 |
T 2 |
|
Sm |
|
|
|
. |
(2.16) |
|||
S |
Д |
|
|
s |
(t)dt |
|
|
|
0,707 S |
m |
|||
T t 0 |
|
|
|
||||||||||
2 |
|||||||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
Для последовательности прямоугольных импульсов, показанной на рис. 2.8а нетрудно показать, что
|
|
1 t 0 |
T |
|
|
|
|
|
|
S |
Д |
|
|
s2 (t)dt Sm |
|
. |
(2.17) |
||
|
|
|
|||||||
|
|
T t 0 |
|
|
T |
|
|||
Эти расчеты проведите самостоятельно.

50
Действующие значения переменных сигналов различной формы являются их энергетическим эквивалентом. Они широко распространены в инженерной практике. Шкалы практически всех амперметров и вольтметров переменного тока градуируются в действующих значениях гармонического сигнала. Напряжение электрической сети дома в розетке или в лаборатории, равное 220 В – это действующее значение гармонического напряжения с частотой 50 Гц, а его амплитуда Um
согласно (2.16) равна Um 220
 2 311В.
2 311В.
Необходимо иметь в виду, что если с помощью амперметра или вольтметра переменного тока (например, тестера) измеряется негармонический сигнал (последовательность прямоугольных импульсов), то показания прибора (действующее значение напряжения) будут ошибочными.
3. РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
3.1. Модель цепи постоянного тока
Если в электрической цепи действуют постоянные напряжения и протекают постоянные токи, то модели реактив-
ных элементов L и C существенно упрощаются. |
|
|
Модель сопротивления R |
остается прежней |
и связь |
между напряжением U и током I |
определяется законом Ома |
|
в виде |
|
|
U RI или |
I U / R . |
(3.1) |
В идеальной индуктивности мгновенные значения напряжения и тока связаны соотношением
u(t) L |
di(t) |
. |
(3.2) |
|
|||
|
dt |
|
|
51
Для постоянного тока i(t) I const его производная по времени равна нулю, следовательно постоянное напряжение на индуктивности равно нулю и ее можно за-
менить коротким замыканием (проводником).
Аналогично в емкости связь между мгновенными значениями напряжения и тока определяется в виде
i(t) C |
du(t) |
. |
(3.3) |
|
|||
|
dt |
|
|
Для постоянного напряжения u(t) U |
const его |
||
производная по времени равна нулю, следовательно постоянный ток через емкость равен нулю и ее можно заменить холостым ходом (разрывом цепи).
Таким образом, в модели цепи постоянного тока присутствуют только сопротивления (модели резисторов) и источники сигнала, а реактивные элементы (индуктивности и емкости) отсутствуют.
3.2. Расчет цепи на основе закона Ома
Этот метод удобен для расчета сравнительно простых цепей с одним источником сигнала. Он предполагает вычисление сопротивлений участков цепи, для которых известна величина тока (или напряжения), с последующим определением неизвестного напряжения (или тока).
Рассмотрим пример расчета цепи, схема которой приведена на рис. 3.1, при токе идеального источника I 1 А и со-
противлениях R1 5 Ом, |
R2 10 Ом, R3 20 Ом. Необходимо |
определить токи ветвей I1 |
и I2 , а также напряжения на сопро- |

|
|
|
|
|
|
|
|
|
|
52 |
|
|
|
|
|
|
|
|
||
тивлениях U1 , U 2 |
и U 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Известен ток источни- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
ка I0 , тогда можно вычислить |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
сопротивление цепи |
RОБЩ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
относительно зажимов источ- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ника тока (параллельного со- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
единения сопротивления R2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
и последовательно соединен- |
||||||||
Рис. 3.1. |
|
|
|
|
|
|
|
|
|
|
|
ных сопротивлений R1 |
и R3 ), |
|||||||
RОБЩ |
|
|
R2 (R1 |
R3 ) |
|
10(5 |
|
20) |
|
7,14Ом . |
|
|||||||||
|
R1 |
R2 |
R3 |
5 |
10 |
20 |
|
|||||||||||||
|
|
|
|
|||||||||||||||||
Тогда напряжение U 2 |
|
на источнике тока (на сопротивлении |
||||||||||||||||||
R2 ) равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U2 |
|
RОБЩ I0 |
7,143 1 |
7,14 В. |
|
||||||||||||||
Затем можно найти токи ветвей |
|
|
|
|
||||||||||||||||
|
I1 |
|
|
U2 |
|
|
|
|
7,143 |
|
|
0,286 А, |
|
|||||||
|
|
R1 R3 |
5 |
|
20 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
I2 |
U2 |
7,143 |
|
0,714А. |
|
|
|||||||||||
|
|
|
|
R2 |
|
|
|
10 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Полученные результаты можно проверить с помощью первого
закона Кирхгофа в виде I1 |
I2 |
I0 . Подставляя вычисленные |
значения, получим I1 I2 |
0,286 |
0,714 1А, что совпадает с |
величиной тока источника. |
|
|
Зная токи ветвей, нетрудно найти напряжения на сопротивлениях (величина U 2 уже найдена)
|
|
53 |
|
|
U1 |
R1I1 |
5 0,286 1,43В, |
||
U3 |
R3 I1 |
20 0,286 |
5,72 |
В. |
По второму закону Кирхгофа U2 U1 |
U3 |
. Складывая полу- |
||
ченные результаты, убеждаемся в его выполнении.
3.3. Общий метод расчета цепи на основе законов Ома и Кирхгофа
Общий метод расчета токов и напряжений в электрической цепи на основе законов Ома и Кирхгофа пригоден для расчета сложных цепей с несколькими источниками сигнала.
Расчет начинается с задания обозначений и положительных направлений токов и напряжений для каждого элемента (сопротивления) цепи.
Система уравнений включает в себя подсистему компонентных уравнений, связывающих по закону Ома токи и напряжения в каждом элементе (сопротивлении) и подсистему топологических уравнений, построенную на основе первого и второго законов Кирхгофа.
Рассмотрим расчет простой цепи из предыдущего примера, показанной на рис. 3.1, при тех же исходных данных.
Подсистема компонентных уравнений имеет вид
U1 |
R1I1, |
|
U2 |
R2 I2 , |
(3.4) |
U3 |
R3I1. |
|
В цепи имеется два узла ( q 2 ) и две ветви, не содер- |
||
жащие идеальных источников тока ( p |
2). Следовательно, |
|
необходимо записать одно уравнение ( q |
1 1) по первому |
|
закону Кирхгофа, |
|
|

|
54 |
|
|
I1 |
I2 |
I0 , |
(3.5) |
и одно уравнение второго закона Кирхгофа ( p |
q 1 1), |
||
U1 |
U3 |
U2 0 , |
(3.6) |
которые и образуют подсистему топологических уравнений. Уравнения (3.4)-(3.6) являются полной системой урав-
нений цепи. Подставляя (3.4) в (3.6), получим
R1I1 R3I1 R2 I2 0 , |
(3.7) |
а, объединив (3.5) и (3.7), получим два уравнения с двумя неизвестными токами ветвей,
|
|
|
I1 |
I2 |
I0 |
, |
|
|
|
(3.8) |
||
|
|
R1I1 |
|
R3I1 |
R2 I |
2 0. |
|
|||||
|
|
|
|
|
||||||||
Выражая из первого уравнения (3.8) ток I2 I0 |
I1 и |
|||||||||||
подставляя его во второе, найдем значение тока I1 , |
|
|
||||||||||
I1 |
|
R2 I0 |
|
|
|
|
10 1 |
|
0,286 |
А, |
(3.9) |
|
|
|
|
|
|
|
|
|
|
||||
|
R1 |
R2 |
R3 |
5 |
10 |
|
20 |
|
|
|||
а затем найдем I2 |
|
I0 I1 |
1 |
0,286 |
|
0,714А. По вычислен- |
||||||
ным токам ветвей из компонентных уравнений (3.4) определим напряжения. Результаты расчета совпадают с полученными ранее в подразделе 3.2.
|
Рассмотрим более сложный пример расчета цепи в схе- |
||||||
ме, |
показанной |
на |
рис. |
3.2, с |
параметрами |
R1 |
1 Ом, |
R2 |
2 Ом, R3 |
3 Ом, |
R4 |
4 Ом, |
R5 5 Ом, |
R6 |
6 Ом, |
55
Рис. 3.2
U1 |
R1 I1 , |
U 4 |
U 2 |
R2 I 2 , |
U 5 |
U 3 |
R3 I3 , |
U 6 |
E0 |
10 В, |
I0 |
1А. |
||
|
Цепь |
содер- |
|||
жит |
q |
4 |
узла |
(их |
|
номера |
указаны |
в |
|||
кружках) |
|
и |
p |
6 |
|
ветвей, не содержащих идеальные источники тока.
Система компонентных уравнений цепи имеет вид
R4 I 4 , |
|
R5 I5 , |
(3.10) |
R6 I 6 . |
|
По первому закону |
Кирхгофа |
необходимо |
записать |
||
q 1 3 уравнения (узел 0 не используется), |
|
||||
узел1 : |
I1 |
I 2 |
I3 |
0, |
|
узел2 : |
I 2 |
I 4 |
I 6 |
0, |
(3.11) |
узел3 : |
I3 |
I 6 |
I5 |
I 0 . |
|
По второму закону Кирхгофа составляется p |
q 1 3 |
||||
уравнения для трех независимых контуров, отмеченных на схеме окружностями со стрелками (внутри указаны номера контуров),
контур1 : U1 |
U2 |
U4 |
E0 , |
|
|
контур2 : |
U3 |
U6 |
U2 |
0, |
(3.12) |
контур3 : |
U6 |
U5 |
U4 |
0. |
|

56
Подставляя (3.11) в (3.13), совместно с (3.12) получим
систему шести ( p |
6) уравнений вида |
|
|
|
|
||||||||
|
|
|
I1 |
I2 |
|
I3 |
0, |
|
|
|
|
|
|
|
|
|
I2 |
I4 |
|
I6 |
0, |
|
|
|
|
(3.13) |
|
|
|
|
I3 |
I6 |
|
I5 |
I0 , |
|
|
|
|
|
|
|
|
|
R1 I1 |
R2 I 2 |
R4 I 4 |
|
E0 , |
|
|
|
|||
|
|
|
R3 I3 |
R6 I 6 |
|
R2 I 2 |
0, |
|
|
|
|||
|
|
|
R6 I 6 |
R5 I5 |
|
R4 I 4 |
0. |
|
|
|
|||
Из второго и третьего уравнений выразим |
|
|
|
||||||||||
|
|
|
|
I 2 |
I 4 |
I6 , |
|
|
|
(3.14) |
|||
|
|
|
|
I3 |
|
I0 |
I5 |
I6 , |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
а из первого |
I1 |
I 2 |
I3 , |
тогда подставив |
I 2 |
и |
I3 , получим |
||||||
I1 I 0 I 4 |
I5 . Подставляя токи I1 , |
I 2 |
и I3 в уравнения вто- |
||||||||||
рого закона Кирхгофа, запишем систему из трех уравнений |
|||||||||||||
|
R1 (I 0 |
I 4 |
I5 ) |
|
R2 (I 4 |
I 6 ) |
R4 I 4 |
E0 , |
|||||
|
R3 (I 0 |
I5 |
I 6 ) R6 I 6 |
R2 (I 4 |
I 6 ) |
|
0, |
||||||
|
|
|
R6 I 6 |
R5 I5 |
|
R4 I 4 |
0, |
|
|
|
|||
которую после приведения подобных запишем в виде |
|||||||||||||
(R1 |
R2 |
R4 )I 4 R1 I5 |
R2 I 6 |
E0 |
R1 I 0 , |
|
|||||||
R2 I 4 |
R3 I5 |
(R2 |
R3 |
|
R6 )I 6 |
R3 I 0 , |
(3.15) |
||||||
|
|
|
R4 I 4 |
R5 I5 |
R6 I 6 |
0. |
|
|
|
|
|||
57
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
R1 |
|
|
R2 |
R4 , |
|
|
|
|
|
|
|
|
|
(3.16) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
R2 |
|
|
R3 |
R6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и из третьего уравнения системы (3.15) запишем |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
R5 I5 |
R6 I 6 |
. |
|
|
|
|
|
|
|
|
|
|
(3.17) |
||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя полученное значение |
I 4 в первые два уравнения |
||||||||||||||||||||||||||||||||||||||
(3.15), получим систему из двух уравнений вида |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
R |
|
|
RR5 |
I |
|
|
|
|
|
R |
|
|
|
AR6 |
I |
|
|
|
|
E |
|
|
R I |
|
, |
|
||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
2 |
|
|
|
|
6 |
|
|
0 |
0 |
||||||||||||||||||
|
|
|
|
1 |
|
|
|
R4 |
|
|
|
|
|
|
R4 |
|
|
|
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.18) |
|||||||||||
|
|
|
|
|
|
|
|
|
R2 R5 |
|
|
|
|
|
|
|
R2 R6 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
R |
|
|
|
I |
|
|
|
|
B |
|
|
I |
|
|
|
R I |
|
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
0 |
|
|
|
||||||||||||
|
|
|
|
|
3 |
|
|
|
|
R4 |
|
|
|
|
|
|
|
|
|
R4 |
|
|
|
|
|
|
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из второго уравнения (3.18) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
I |
|
|
|
|
|
BR4 |
|
|
R2 R4 |
I 6 |
|
|
R3 R4 I 0 |
, |
|
|
|
|
(3.19) |
||||||||||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
R3 R4 |
|
R2 R5 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
тогда из первого уравнения найдем ток I 6 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
R R |
|
|
R R (E |
|
|
|
R I |
|
) |
|
R |
|
|
AR5 |
|
|
R R |
|
I |
|
|
|||||||||||||||||
4 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
4 |
0 |
|
||||||||||||||||||||||||
3 |
|
|
|
2 |
5 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
R4 |
|
|
3 |
|
|
|
|||||||||||||
I 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. (3.20) |
||
|
|
|
|
|
|
|
|
|
|
|
AR5 |
|
|
|
|
|
AR6 |
|
|
|
|
|
|
|
|
||||||||||||||
|
BR4 |
R2 R6 |
|
|
R1 |
|
|
R2 |
|
R3 R4 |
|
R2 R5 |
|||||||||||||||||||||||||||
|
|
|
|
|
R4 |
|
|
|
|
|
|
R4 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
