
Начала математического анализа. Часть 3. Горбунов В.В., Соколова О.А
.pdf
3. Корни k1 и k2 характеристического уравнения являются
комплексными: |
|
|
k1 |
|
i , |
|
k2 |
i |
|||||
|
p 2 |
p |
|
|
|
|
p 2 |
|
|
||||
D |
|
g 0, |
|
, |
|
g |
|
|
0 |
. В этом случае ча- |
|||
4 |
2 |
4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
стными решениями дифференциального уравнения является функ-
ции y |
e i x и y |
2 |
e i x , которые образуют фундаменталь- |
1 |
|
|
ную систему решений дифференциального уравнения, но не удобны для конкретного использования.
|
|
Применяя |
|
|
формулы |
Эйлера |
ei |
cos |
|
i sin |
, |
|||||||||||||
e i |
|
cos |
|
i sin |
можно получить два действительных частных |
|||||||||||||||||||
линейно независимых решения дифференциального уравнения |
~ |
и |
||||||||||||||||||||||
y1 |
||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
y1 |
y2 |
e x i x |
e x i x |
|
x ei x |
e i x |
|
x |
|
|
|
|
||||||||||
y1 |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
e |
|
cos |
x , |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
~ |
|
|
y1 |
y2 |
|
e |
x i x |
e x i x |
|
|
x ei x |
e i x |
|
|
x |
|
|
|
||||||
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
e |
|
sin |
x . |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Функции |
~ |
|
~ |
являются решениями дифференциального |
||||||||||||||||||
|
|
y1 |
и y2 |
|||||||||||||||||||||
уравнения по теореме о свойстве решений этого уравнения и обра-
зуют фундаментальную систему решений, так как W x |
0 . Поэто- |
||||||||||
му |
общее |
решение |
дифференциального |
уравнения |
|||||||
y |
py |
qy |
0 |
|
в |
|
третьем |
случае запишется |
в |
виде |
|
y |
e x |
c cos |
x c |
2 |
sin |
x . |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Пример. 12. Найти общее решение дифференциального урав- |
||||||||||
нения y |
4y |
13y |
|
0 . |
|
|
|
|
|
||
|
Решение: |
Составим |
|
характеристическое |
уравнение |
||||||
k 2 |
4k |
13 |
0 , которое имеет два комплексных корня k |
2 |
3i и |
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
k2 |
2 |
3i . Запишем общее решение дифференциального уравнения в |
|||||||||
виде y |
e2x c sin3x |
c |
2 |
cos3x . |
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
||
21

1.11. Линейные неоднородные дифференциальные уравнения второго порядка
Рассмотрим линейные неоднородные дифференциальные уравнения второго порядка
|
y |
a1 x y a2 x y f x , |
где a1 x , a2 |
x , f x - |
заданные, непрерывные на (a,b) функции. |
Уравнение y |
a1 x y |
a2 x y 0 , называется соответствующим |
ему однородным уравнением.
Теорема 1. (Теорема о структуре общего решения линейного неоднородного дифференциального уравнения второго порядка).
Общим решением yон уравнения y a1 x y a2 |
x y |
f x яв- |
||
ляется сумма его произвольного частного решения |
yчн |
и общего |
||
решения yoo |
c1 y1 |
c2 y2 соответствующего однородного уравне- |
||
ния, т.е. yон |
yоо |
yчн . |
|
|
Доказательство. Убедимся при помощи подстановки, что |
||||
функция yон |
yоо |
yчн - решение уравнения |
|
|
|
y |
a1 x y a2 x y f x . |
|
|||||
Так как yoo есть решение уравнения |
|
|
||||||
|
|
y a1 x y a2 x y 0 , |
|
|||||
а yчн |
- решение уравнения |
|
|
|
|
|||
|
y |
a1 x y a2 x y f x , |
|
|||||
то |
|
|
|
|
|
|
|
|
yoo |
yчн |
a1 |
x |
yоо |
yчн |
a2 |
x yоо |
yчн |
yоо |
a1 x yоо |
a2 x yоо |
yчн |
a1 x yчн |
a2 x yчн |
|||
|
|
|
0 |
f |
x |
f x . |
|
|
Это означает, что функция |
yоо |
yчн |
является решением ис- |
|||||
ходного дифференциального уравнения. Для доказательства того,
что функция |
yон |
yчн |
c1 y1 |
c2 y2 |
является общим решением |
|
уравнения y |
a1 |
x y |
a2 x y |
f |
x |
надо доказать, что из ре- |
шения yон |
yчн |
c1 y1 |
c2 y2 |
можно |
выделить единственное |
|
22

частное решение, удовлетворяющее заданным начальным услови-
ям y x0 |
y0 , y x0 |
y0 . |
Это означает, |
что функция yоо yчн является решением ис- |
|
ходного дифференциального уравнения. Для доказательства того,
что функция |
yон |
yчн |
c1 y1 |
c2 y2 |
является общим решением |
|
уравнения y |
a1 |
x y |
a2 x y |
f |
x |
надо доказать, что из ре- |
шения yон |
yчн |
c1 y1 |
c2 y2 |
можно |
выделить единственное |
|
частное решение, удовлетворяющее заданным начальным услови-
ям y x0 |
y0 , y x0 |
|
y0 . |
|
|
|
|
|
Продифференцировав |
функцию |
yон |
yчн c1 y1 c2 y2 и |
|||||
подставив |
yон и yон |
в начальные условия получим систему уравне- |
||||||
ний относительно с1 |
и с2 : |
|
|
|
|
|
||
|
c1 y1 |
x0 |
c2 y2 |
x0 |
y0 |
yчн x0 |
, |
|
|
c1 y1 |
x0 |
c2 y2 |
x0 |
y0 |
yчн x0 |
, |
|
где y0 |
yон x0 , y0 |
|
yон |
x0 . Определителем этой системы явля- |
||||
ется определитель Вронского W x0 |
для функции y1 x |
и y2 x в |
точке x x0 . Функции y1 x и y2 x |
линейно независимы и обра- |
|
зуют фундаментальную систему решений, т. е. W x0 |
0 . Следова- |
|
тельно, система имеет единственное решение для c1 и c2 . Поэтому решение y yчн c1 y1 x c2 y2 x является частным решением
уравнения y a1 x y
a1 x y a2 x y
a2 x y 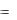 f x , удовлетворяющим задан-
f x , удовлетворяющим задан-
ным начальным условиям, что и требовалось доказать.
При нахождении частных решений линейных неоднородных дифференциальных уравнений используется следующая теорема.
Теорема 2. (Теорема о наложении решений). Если правая
часть уравнения |
y |
a1 |
x y |
|
a2 |
x y |
f1 x |
f2 |
x представляет |
|||
собой сумму двух функций: |
f1 |
x |
и f2 |
x , а y1чн |
и y2чн - частные |
|||||||
решения |
|
уравнений |
|
|
y |
a1 |
x y |
a2 |
x y f1 x |
|||
и y |
a1 x y |
a2 |
x y |
f2 |
x |
|
соответственно, |
то |
функция |
|||
yчн |
y1чн |
y2чн |
является решением данного уравнения. |
|||||||||
23

Действительно,
y1чн |
y2чн |
a1 x y1чн |
y2чн |
a2 x y1чн |
y2чн |
y1чн |
a1 x y1чн |
a2 x y1чн |
y2чн |
a1 x y2чн |
a2 x y2чн |
|
|
f1 x |
f2 x |
f x . |
|
1.12. Интегрирование линейного неоднородного дифференциального уравнения второго порядка с постоянными коэф-
фициентами и правой частью специального вида
Рассмотрим неоднородное линейное дифференциальное урав-
нение |
y |
|
py |
|
qy |
e x |
P |
|
|
x cos x |
Q |
x sin x |
с |
правой |
|||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
m |
|
|
|
|
|
|
частью |
специального |
вида, |
|
где |
|
, |
, p, q |
– |
некоторые числа, |
||||||||||
P x |
a |
n |
xn |
a |
n 1 |
xn 1 |
... |
a |
0 |
, Q |
m |
x |
b xm |
b |
|
xm 1 |
... |
b . |
|
n |
|
|
|
|
|
|
|
|
m |
m 1 |
|
|
0 |
||||||
Общее решение уравнения представляет собой сумму общего |
|||||||||||||||||||
решения соответствующего однородного уравнения yoo |
и частного |
||||||||||||||||||
решения yчн |
неоднородного уравнения. Частное решение уравнения |
||||||||||||||||||
со специальной правой частью может быть найдено методом неопределенных коэффициентов, состоящим в том, что по виду правой
части |
f x e x P |
x cos x |
Q |
m |
x sin |
x |
неоднородного урав- |
||
|
n |
|
|
|
|
|
|
|
|
нения записывают ожидаемую форму частного решения |
|||||||||
|
y |
xl e x |
P |
x cos x |
Q |
N |
x sin x . |
||
|
|
|
N |
|
|
|
|
|
|
Здесь многочлены PN |
x , |
QN |
x |
с коэффициентами, подлежащими |
|||||
определению, имеют одинаковую степень, равную большему из значений чисел m и n . Число l равно кратности совпадения параметра 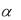 i
i с корнями характеристического уравнения. Если параметр
с корнями характеристического уравнения. Если параметр
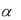 i
i не совпадает с корнями характеристического уравнения, то
не совпадает с корнями характеристического уравнения, то
l 0 . Если параметр оказывается равным одному из действительных корней характеристического уравнения, или совпадает с одним из комплексных корней характеристического уравнения, то l 1. Если параметр совпадает с двукратным корнем характеристического уравнения, то l 2 .
Рассмотрим несколько частных случаев.
24

1. Пусть правая часть неоднородного уравнения имеет вид
f x |
P ( x)e x , |
где P (x) - многочлен |
n –ой |
степени. Параметр |
|||
|
n |
|
n |
|
|
|
|
правой части |
i |
совпадает с |
, а число |
не является кор- |
|||
нем |
характеристического уравнения |
k 2 |
pk |
q 0. В этом слу- |
|||
чае частное решение ищется в виде |
|
|
|
||||
|
|
y |
( A xn |
A xn 1 |
... A )e x , |
||
|
|
|
0 |
1 |
|
n |
|
где коэффициенты A0 , |
A1 ,…, An |
подлежат определению. |
|||||
|
Если же число |
совпадает с одним из действительных корней |
|||||
характеристического уравнения, то частное решение ищется в виде
y |
x( A xn |
A xn 1 ... |
A )e x . |
|
0 |
1 |
n |
Если же число |
совпадает с двукратным действительным кор- |
||
нем характеристического уравнения, то частное решение ищется в виде
y |
x2 ( A xn |
|
A xn 1 ... |
A )e x . |
||
|
|
0 |
|
|
1 |
n |
Пример 13. Найти общее решение уравнения |
||||||
|
|
y 4y |
|
3y x 2 . |
|
|
Решение: Общее решение соответствующего однородного |
||||||
уравнения имеет вид |
|
|
|
|
|
|
y |
оо |
C e x |
C |
2 |
e3x . |
|
|
1 |
|
|
|
||
Так как правая часть данного неоднородного уравнения имеет вид
x 2 e0x , где параметр правой части |
i =0 и не совпадает с |
||||||||||
корнями характеристического уравнения k1 |
1 и |
|
k2 |
3 , то част- |
|||||||
ное решение ищется в виде |
y |
чн |
Q (x)e0 x |
Ax |
B . |
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
Подставляя это выражение в заданное уравнение, имеем |
|||||||||||
|
4A 3(Ax B) x |
2 . |
|
|
|
|
|
|
|||
Приравнивая коэффициенты при одинаковых степенях х, по- |
|||||||||||
лучим |
|
|
|
|
|
|
|
|
|
|
|
3A |
1, |
|
4A |
3B 2 , |
|
|
|
|
|
|
|
откуда A 1/ 3, B |
10 / 9. Следовательно, |
yчн |
|
1 |
x |
|
10 |
. |
|||
|
|
9 |
|||||||||
|
|
|
|
|
|
3 |
|
||||
Общее решение дифференциального уравнения равно
25

y C1e x C2e3x 13 x 109 .
Пример 14. Найти общее решение дифференциального урав-
нения
y 5y
5y 4y (x 2)ex .
4y (x 2)ex .
Решение: Общее решение соответствующего однородного уравнения имеет вид
yоо C1e x C2e4 x .
Так как правая часть данного неоднородного уравнения имеет вид
x 2 ex , где параметр правой части |
i =1 и совпадает с корнем |
|||||||||||
характеристического уравнения k1 |
1 , |
то частное решение ищется |
||||||||||
в виде |
y |
чн |
xQ (x)e x |
( Ax 2 |
Bx)e x . |
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Найдя первую производную |
y |
Ax2 |
2A |
B x |
B ex и |
|||||||
вторую производную y |
|
|
Ax2 |
|
4A |
B x |
2A |
2B ex и под- |
||||
ставляя это выражение в заданное уравнение, имеем |
|
|
||||||||||
Ax 2 |
4A B x 2A 2B e x |
5 Ax 2 |
2A B x B e x 4 Ax 2 |
Bx e x |
||||||||
x |
2 e x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6Ax 4A 3B ex |
x 2 ex . |
|
|
||||||
Приравнивая коэффициенты при одинаковых функциях xex , |
||||||||||||
e x получим |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
6A |
1, |
2A |
3B |
2 , |
|
|
|
||
откуда |
|
|
A |
1/ 6, B |
5 / 9. |
|
|
Следовательно, |
||||
yчн |
|
x 2 / 6 5x / 9 e x . |
|
|
|
|
|
|
|
|
||
Общее решение дифференциального уравнения равно |
|
|||||||||||
|
|
|
y C ex |
C |
2 |
e4x |
( x2 / 6 5x / 9)ex . |
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Пример 15. Найти общее решение уравнения y 4 y xex .
4 y xex .
Решение: Найдем общее решение однородного уравнения, предварительно записав его характеристическое уравнение
26

k 2 4 |
0, |
k |
2i . |
Общее решение |
соответствующего |
одно- |
|
|
|
1,2 |
|
|
|
|
|
родного уравнения |
|
|
|
|
|||
|
|
|
yоо |
C1 cos2x |
C2 sin 2x . |
|
|
Правая |
часть |
данного неоднородного |
уравнения xex |
имеет |
|||
вид P (x)e x . Так как коэффициент |
i |
1 в показателе степени |
|||||
1 |
|
|
|
|
|
|
|
не является корнем характеристического уравнения, то частное ре-
шение ищется в виде |
yчн |
( Ax |
B)e x . Подставляя это выражение |
|||||||||||||
в заданное уравнение, будем иметь |
|
|
|
|
|
|
||||||||||
|
|
|
|
(Ax 2A B)ex |
4(Ax B)ex |
xex . |
|
|
||||||||
Приравнивая коэффициенты при одинаковых функциях, получим |
||||||||||||||||
|
|
|
|
|
5A |
1, |
2A |
5B |
0, |
|
|
|
|
|
||
откуда |
A |
1/ 5, |
|
B |
2 / 25. |
Следовательно, частное |
решение |
|||||||||
равно yчн |
(x / 5 |
|
2 / 25)e x . |
|
|
|
|
|
|
|
|
|||||
Общее решение равно |
|
|
|
|
|
|
|
|
|
|
||||||
y |
C cos2x |
C |
2 |
sin 2x |
x / 5 |
2 / 25 e x . |
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Правая часть неоднородного уравнения имеет вид |
|
|
|||||||||||||
|
|
|
|
f x |
x |
P x cos x |
Q |
m |
x sin x , |
|
|
|||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
где Рп(х) и Qm(x) - многочлены степени п и т соответственно, |
и |
|||||||||||||||
|
- действительные числа. |
|
|
|
|
|
|
|
|
|||||||
|
В |
этом |
случае |
частное |
решение |
|
следует искать в |
виде |
||||||||
y |
xl x |
M s |
x cos |
x |
N s |
x sin x , где l - |
число, равное крат- |
|||||||||
ности |
|
|
i |
|
как |
корня |
характеристического |
уравнения |
||||||||
k 2 |
pk |
|
g |
0 , M s |
x и N s |
x |
- многочлены степени s |
с неопре- |
||||||||
деленными коэффициентами, |
s |
- наивысшая степень многочленов |
||||||||||||||
Рп(х) и Qm(x), т. е. s |
= max(n, m). |
|
|
|
|
|
|
|
||||||||
|
Следует отметить, что указанные формы частных решений со- |
|||||||||||||||
храняются и в том случае, когда правая часть дифференциального
уравнения имеет вид |
P (x)e |
x cos x или |
Q |
m |
(x)e x sin x . |
|
n |
|
|
|
|
Если же правая часть линейного уравнения второго порядка |
|||||
имеет вид: |
|
|
|
|
|
|
f (x) |
M cos x |
N sin |
x , |
|
27

где M и N – постоянные числа, а i не является корнем характери-
не является корнем характери-
стического уравнения, то частное решение уравнения следует искать в виде
yчн A cos x B sin x .
Если i является корнем характеристического уравнения, то частное решение уравнения следует искать в виде
является корнем характеристического уравнения, то частное решение уравнения следует искать в виде
|
|
|
|
yчн |
x( A cos |
x |
B sin |
x) . |
||
Пример 16. Найти общее решение линейного неоднородного |
||||||||||
уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 y |
5y |
2 cos x. |
|
||
Решение: Общее решение будет иметь вид |
y yoo yчн . Со- |
|||||||||
ставим характеристическое уравнение и найдем его корни |
||||||||||
k 2 |
2k 5 0, |
k1 |
1 2i, |
|
k2 |
1 2i. |
||||
Тогда общее решение соответствующего однородного уравнения |
||||||||||
|
|
y |
oo |
e |
x (C cos2x |
C |
2 |
sin 2x).. |
||
|
|
|
|
1 |
|
|
|
|
||
Поскольку параметр правой части данного неоднородного |
||||||||||
уравнения |
i |
|
i |
не |
является |
корнем характеристического |
||||
уравнения, частное решение будем искать в форме |
||||||||||
|
yчн |
A cos x |
B sin x , |
|
|
|
|
|||
где А и В – постоянные коэффициенты, подлежащие определению. Находя производные и подставляя их в заданное уравнение,
будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Acosx Bsin x |
2( |
Asin x |
Bcosx) 5(Acosx |
|
Bsin x) |
2cosx . |
||||||||||||
Приравнивая коэффициенты при cos x и sin x , получим: |
||||||||||||||||||
|
|
|
|
|
|
A 2B 5A 2, |
B 2 A 5B 0 , |
|
||||||||||
откуда |
|
A |
2 / 5, |
B |
1 / 5. |
Следовательно, |
частное |
решение |
||||||||||
yчн |
2 |
cos x |
|
1 |
sin x . |
Общее решение |
y yoo |
|
yчн будет иметь |
|||||||||
5 |
5 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
e x (C cos2x |
C |
|
sin 2x) + |
2 |
cos x |
|
1 |
sin x . |
||||||
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
|
|
5 |
|
|
5 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|

Пример 17. Найти общее решение линейного неоднородного уравнения y  4 y cos 2x.
4 y cos 2x.
Решение: Найдем общее решение соответствующего однородного уравнения. Составим характеристическое уравнение и найдем его корни
k 2 4 0, |
k1 |
2i, |
k2 |
2i. |
Тогда общее решение соответствующего однородного уравнения yoo C1 cos2x C2 sin 2x. .
Поскольку параметр правой части  i
i 2i совпадает с
2i совпадает с
корнем характеристического уравнения, частное решение будем искать в форме
yчн x( A cos x B sin x),
где А и В – постоянные коэффициенты, подлежащие определению.
|
Подставляя производные |
|
|
|
|
|
|
|
|
|
|
||||||||
|
yчн |
2x( |
Asin 2x |
B cos2x) |
( A cos2x |
B sin 2x), |
|
||||||||||||
|
yчн |
4x( A cos2x |
B sin 2x) |
4( |
Asin 2x |
B cos2x) |
|
||||||||||||
в исходное уравнение, и приравнивая коэффициенты при |
cos 2x |
и |
|||||||||||||||||
sin 2x , |
получим |
|
два |
уравнения |
|
для |
определения |
А и |
В: |
||||||||||
4B |
1, |
4A |
0 . |
|
Откуда |
A |
0, |
|
B |
1 / 4. Следовательно, част- |
|||||||||
ное решение yчн |
|
1 |
x sin x . Общее решение будет иметь вид |
|
|||||||||||||||
4 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y |
C cos 2x |
C |
|
sin 2x + |
1 |
x sin x . |
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 18. Найти частное решение линейного неоднородного |
||||||||||||||||||
уравнения, |
|
удовлетворяющее |
|
|
начальным |
условиям. |
|||||||||||||
y(0) |
1, |
|
y (0) |
2. . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
y |
y |
2 y |
cos x |
3sin x. |
|
|
|
|||||
|
Решение: Найдем общее решение дифференциального уравне- |
||||||||||||||||||
ния y |
yoo |
yчн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Составим характеристическое уравнение и найдем его корни:
k 2 k 2 0, |
k1 1, |
k2 |
2. |
Общее решение соответствующего однородного уравнения имеет вид
29

|
y |
oo |
C e x |
C |
2 |
e 2 x . |
|
|
1 |
|
|
||
Правая часть данного неоднородного уравнения имеет вид |
||||||
|
f ( x) |
e x (M cos x N sin x) . |
||||
Так как число |
i |
i |
не является корнем характеристиче- |
|||
ского уравнения, то частное решение будем искать в форме |
||||||
|
yчн |
( A cos x |
B sin x), |
|||
Находя производные и подставляя в исходное уравнение, получим
(B 3A) cos x ( A 3B) sin x cos x 3sin x.
Приравняем коэффициенты при cos x и sin x , получим уравнения для определения A и В:
|
|
B |
3A 1, |
3B A 3., |
|
||||
откуда A |
0, |
B |
1. |
Следовательно, частное решение yчн sin x . |
|||||
Общее решение будет иметь вид |
|
|
|
||||||
|
y |
C1e x |
C2 e 2 x |
sin x . |
|
||||
Найдем С1, С2, используя начальные условия |
|||||||||
C1e0 |
C2 e0 |
sin 0 |
1; |
или |
C1 |
C2 |
1; |
||
C1e0 2C2 e0 |
cos 0 |
2, |
C1 |
2C2 1 |
2. |
||||
|
|||||||||
Отсюда С1=1, С2=0. Искомое частное решение будет иметь вид
ye x  sin x .
sin x .
1.13.Метод вариации произвольных постоянных
Частное решение yчн .уравнения y a1 x y
a1 x y a2 x y
a2 x y  f x
f x
с правой частью произвольного вида можно найти, если известно общее решение yoo соответствующего однородного уравнения мето-
дом вариации произвольных постоянных.
За основу берется общее решение однородного дифференциального уравнения yoo c1 y1 x c2 y2 x . Заменим в общем ре-
шений постоянные c1 и c2 неизвестными функциями c1 x и c2 x и подберем их так, чтобы функция
30
