
2258
.pdf
где a |
C |
, |
b |
C |
. Числа a |
и b равны величинам отрезков, |
|
A |
B |
||||||
|
|
|
|
|
|||
которые отсекает прямая на осях |
Ox и O у от начала координат, |
||||||
соответственно.
Выбирая в уравнении прямой общего вида нормальный вектор единичной длины, получим нормальное уравнение прямой на
плоскости |
|
|
|
|
|
|
|
|
||||
|
Ax |
By C |
0 или |
x cos y cos 0 . |
(7.4) |
|||||||
|
|
|
|
|||||||||
|
||||||||||||
|
|
A2 B2 |
|
|
|
|
|
|
|
|
||
Расстояние d от произвольной точки М0 (x0;y0) до прямой (7.2) |
||||||||||||
определяется формулой |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
d |
|
Axo |
Byo C |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
A2 B2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Пример 7.1. Даны вершины треугольника A(5;1) , |
B(3; 2) , |
|||||||||||
C( 1;1) . Составить уравнение высоты AD.
Решение. Так как высота AD перпендикулярна стороне BC , то
|
|
вектор BC 4;3 является вектором нормали для прямой |
AD . |
Тогда общее уравнение прямой AD имеет вид |
|
4(x 5) 3( y 1) 0 или 4x 3y 17 0. |
|
7.2. Каноническое уравнение прямой
Если ориентацию прямой на плоскости описывать с помощью
|
l; m и ввести точку |
направляющего вектора прямой q = |
M1 ( x1 , y1 ), принадлежащую прямой, то из условия параллельности |
|||||||
|
|
x x1; y y1 легко получить каноническое |
|||||
векторов q |
и М1М = |
||||||
уравнение прямой |
|
|
|
|
|
|
|
|
|
|
x x1 |
|
y y1 |
. |
(7.5) |
|
|
|
|
|
|||
|
|
|
l |
m |
|
||
60
Если в качестве направляющего вектора взять вектор
|
|
y1 , |
|
|
|
|
|
|
|
|
|
||
М1М 2 = x2 |
x1 ; y2 |
то |
можно |
получить |
уравнение прямой, |
||||||||
проходящей через две данные точки M1 (х1, у1), |
M 2 (х2,у2): |
||||||||||||
|
|
|
х х1 |
|
|
у у1 |
. |
(7.6) |
|||||
|
|
|
|
|
х |
|
|
||||||
|
|
|
х |
2 |
|
|
у |
2 |
у |
|
|||
|
|
|
|
1 |
|
|
|
1 |
|
|
|||
Пример 7.2. Составить каноническое уравнение медианы АЕ треугольника c вершинами A(1;3); B( 2; 4);C(5;2).
Решение. Медиана АЕ делит сторону ВС пополам. Тогда, используя формулу для нахождения координат точки, делящей отрезок в заданном соотношении (4.8), найдем координаты точки Е.
x |
|
|
xB xC |
2 5 |
3 |
; |
E |
|
|
||||
|
2 |
2 |
2 |
|
||
|
|
|
||||
|
|
|
y |
|
|
|
|
yB yC |
4 2 1. |
|
|
||||||||||
E |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Зная координаты |
|
точки |
|
Е( |
3 |
; 1) |
и |
А(1;3) , |
составим |
||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
каноническое уравнение прямой, проходящей через две точки |
|||||||||||||||||||||
|
|
x 1 |
|
|
|
y 3 |
|
или |
x 1 |
|
y 3 |
. |
|
|
|||||||
|
3 |
1 |
|
|
1 3 |
|
1 |
|
|
4 |
|
|
|||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
Пример 7.3. Даны вершины треугольника: |
А(1;1) , |
B(10;13) , |
|||||||||||||||||||
C(13;6) . Составить уравнение биссектрисы угла А.
Решение. Пусть точка D – точка пересечения биссектрисы со стороной ВС. Из свойства биссектрисы внутреннего угла
треугольника |
следует, |
|
|
|
|
что |
|
|
|
BD |
|
|
|
|
|
|
|
AB |
|
|
|
|
. |
Но |
|||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
DC |
|
|
|
|
|
|
AC |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
AB |
|
(10 1)2 |
(13 1)2 15 , |
|
AC |
|
|
(13 1)2 |
|
(6 1)2 |
13. |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
Следовательно, DCBD 1513.
61

Так как известно отношение, в котором точка D делит отрезок ВС , то координаты точки D определятся по формулам
10 (15 |
)13 |
13 (15 |
)6 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
13 |
|
, y |
|
|
|
13 |
, |
|
т.е. |
D(325 |
|
; 259 |
) . |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 15 |
|
|
|
|
|
|
1 15 |
|
|
|
|
|
|
|
|
|
28 |
|
28 |
||
|
|
13 |
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|||
Задача сводится |
к составлению |
уравнения |
прямой, |
проходящей |
||||||||||||||||||
|
|
|
|
|
y 1 |
x 1 |
|
|
|
|
7x 9y 2 0. |
|
||||||||||
через точки А и D : |
|
|
|
, т.е. |
|
|||||||||||||||||
25928 1 |
32528 1 |
|
||||||||||||||||||||
|
7.3. Параметрические уравнения прямой |
|
|
|
||||||||||||||||||
Примем |
за |
|
параметр t |
величину |
|
х х1 |
|
у у1 |
= t, |
где |
||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
m |
|
|
|
t . |
Тогда, |
|
находя |
выражения |
для |
x |
и |
y, |
получим |
|||||||||||||
параметрические уравнения прямой на плоскости: |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x lt x1 , |
|
|
|
|
|
|
|
|
(7.7) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y mt y1 . |
|
|
|
|
|
|
|
|
|
||||
7.4. Уравнения прямой с угловым коэффициентом |
|
|||||||||||||||||||||
Уравнение |
прямой |
с угловым |
коэффициентом |
y kx b |
||||||||||||||||||
(школьное уравнение) является отражением того, что прямая является единственным геометрическим объектом на плоскости, описывающим линейную зависимость между переменными x и y .
Если же имеется точка M1 (x1 , y1 ) , принадлежащая прямой, и угловой коэффициент k tg , то можно заметить, что независимо от положения текущей точки прямой M (x, y) будет выполняться
соотношение, |
называемое уравнением |
прямой с |
угловым |
|||
|
|
|
|
|
||
коэффициентом, проходящей через заданную точку: |
|
|||||
|
|
k |
y y1 |
. |
|
(7.8) |
|
|
|
|
|||
|
|
|
x x |
|
|
|
|
1 |
|
|
|
||
7.5. Угол между двумя прямыми.
Условие параллельности и перпендикулярности двух прямых
62

Пусть прямые L1 |
и L2 заданы общими уравнениями |
|
|||||||||||||||||||||||||
A1 x B1 y C1 0 и |
A2 x B2 y C2 |
0. |
|
Задача об определении |
|||||||||||||||||||||||
угла между |
прямыми |
сводится |
|
к |
определению угла |
между |
|||||||||||||||||||||
|
|
|
|
|
|
|
A1 ; B1 |
|
|
|
= A2 ; B2 по известной |
||||||||||||||||
нормальными векторами |
n1 = |
и n2 |
|||||||||||||||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
A1 A2 B1 B2 |
|
|
, |
(7.9) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A2 B 2 |
|
A2 |
B 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
2 |
|
2 |
|
|
|
||||
где угол между прямыми. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Условие |
|
параллельности |
|
|
|
эквивалентно |
условию |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
коллинеарности векторов |
n1 и |
n2 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
A1 |
|
|
B1 |
|
. |
|
|
|
|
|
|
|
|
|
(7.10) |
||||
|
|
|
|
|
|
|
|
A2 |
|
B2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Условие |
|
перпендикулярности |
|
|
|
прямых |
|
|
соответствует |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
перпендикулярности векторов |
n1 |
и |
|
n2 : |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
A1 A2 B1B2 0 . |
|
|
|
|
(7.11) |
||||||||||||||||
Если прямые L1 и L2 |
заданы каноническими уравнениями: |
||||||||||||||||||||||||||
|
|
х х1 |
|
|
у у1 |
|
|
|
х х2 |
|
|
у у2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
l1 |
|
|
m1 |
, |
|
|
|
|
l2 |
|
|
|
|
|
m2 |
, |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где направляющие векторы q1 = {l1, m1} |
|
и |
q2 |
= {l2, m2}, тогда |
|||||||||||||||||||||||
косинус угла между прямыми вычисляется по формуле:
cos = |
|
|
l1l2 |
m1m2 |
|
, |
(7.12) |
||||
|
|
|
|
|
|
|
|
||||
l 2 |
m |
2 l |
2 m 2 |
||||||||
|
|
|
|
|
|||||||
1 |
1 |
2 |
2 |
|
|
|
|||||
а условия параллельности и перпендикулярности прямых принимают вид
|
l1 |
|
m1 |
, |
(7.13) |
|
|
l2 |
m2 |
||||
|
|
|
|
|
||
l1l2 m1m2 |
0 . |
(7.14) |
||||
63
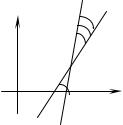
Если прямые |
L1 и L2 |
заданы уравнениями |
с угловыми |
коэффициентами |
y k1 x b1 |
и y k2 x b2 , то |
может быть |
вычислен тангенс угла между прямыми по формуле |
|
||
|
tg tg ( |
|
|
|
) |
tg 2 tg 1 |
|
k2 k1 |
, |
(7.15) |
|
1 |
2 |
|
|
||||||
|
|
|
1 tg 1tg 2 |
1 k1k2 |
|
|||||
|
|
|
|
|
|
|||||
где 1 |
и 2 - углы наклона прямых. |
|
|
|
|
|||||
у
0 1  2 x
2 x
Рис. 13
Условие параллельности прямых определяется как случай tg 0 , т.е.
|
k1 k2 |
(7.16) |
|||
Условие перпендикулярности – это условие того, что tg не |
|||||
существует, т.е. k1k2 1 0 или |
|
|
|
||
k |
|
|
1 |
(7.17) |
|
2 |
k1 |
||||
|
|
|
|||
|
|
|
|
||
Вопросы для самопроверки
1.Как записывается общее уравнение прямой на плоскости?
2.Как записываются параметрические уравнения прямой на плоскости?
64
3.Что называется угловым коэффициентом прямой на плоскости и каков его геометрический смысл в декартовой прямоугольной системе координат?
4.Как записывается уравнение прямой, проходящей через две точки на плоскости?
5.Как вычисляются углы между двумя прямыми на плоскости? Каковы условия параллельности и перпендикулярности двух прямых на плоскости?
8.КРИВЫЕ ВТОРОГО ПОРЯДКА
Впрямоугольной системе координат, в плоскости Oxy уравнение второй степени
Ах2 + 2Вху +Су2 +2Dх + 2Еу +F = 0 |
(8.1) |
определяет кривую второго порядка, где А, В, С, D, E, F заданные действительные числа. При этом А,В,С одновременно не равны нулю.
Известный частный случай дает уравнение окружности:
x2 y 2 |
a2 , |
a 0 . |
(8.2) |
8.1. Каноническое уравнение эллипса
Эллипсом называется геометрическое место точек плоскости, для каждой из которых суммы расстояний до двух фиксированных
точек F1 ( с, о) и F2 (с, о) , называемых фокусами, есть величина постоянная 2a , большая, чем расстояние между фокусами .
65
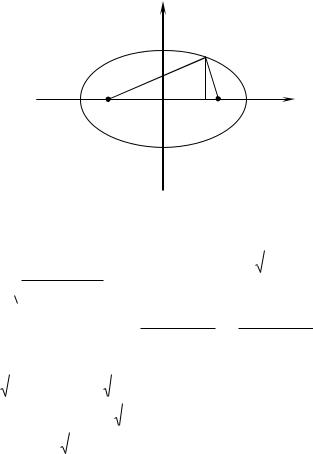
Y |
|
|
|
|
|
B |
M(x,y) |
|
|
|
|
|
||
r1 |
|
r2 |
|
X |
|
|
|
||
|
|
|
|
|
F1(-C,0) |
|
F2(C,0) |
A |
|
|
|
|
|
|
Рис.14 |
|
|
|
Пусть расстояния от текущей |
точки эллипса M (x, y) |
до |
|
|
|
|
|
фокусов F1 ( с, о) и F2 (с, о) равны |
r1 F1M |
x c 2 y 2 |
и |
r2 F2 M 
 x c 2 y 2 , соответственно (рис. 18). Тогда уравнение эллипса имеет вид
x c 2 y 2 , соответственно (рис. 18). Тогда уравнение эллипса имеет вид
F1M F2 M 2a или 
 x c 2 y2
x c 2 y2 
 x c 2 y2 2a .
x c 2 y2 2a .
Преобразуем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a x c 2 y2 x c 2 y2 ; |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
4a2 x c 2 y2 4a x c 2 y2 x c 2 y2 ; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
4a2 4cx 4a x c 2 y2 ; |
|
|
|
||||||||||||
a4 2a2cx c2 x2 a2 x2 2cx c2 y2 |
; |
|
|||||||||||||
a4 a2c2 c2 x2 a2 x2 a2 y2 . |
|
|
|
||||||||||||
Обозначая b2 a2 c2 , имеем a2b2 |
b2 x2 a2 y2 или |
|
|||||||||||||
|
|
|
|
|
|
х 2 |
|
|
у 2 |
1 |
, |
а b |
(8.3) |
||
|
|
|
|
|
|
а 2 |
|
|
|||||||
|
|
|
|
|
|
|
|
b2 |
|
|
|
||||
- каноническое уравнение эллипса.
66
Если в уравнении заменить х на – х, у на – у, то уравнение не изменится. Это значит, что эллипс - кривая симметричная относительно осей Ох и Оу.
Величины а и b называются большой и малой полуосями
эллипса, т.к. а b . Эллипс проходит через точки (0, b ) и (а,0) или (0, - b ) и (- а,0), которые называются вершинами эллипса.. Эллипс - непрерывная замкнутая кривая, которая находится внутри
прямоугольника x а; у b .
Эксцентриситетом эллипса называется величина
e |
с |
|
1 |
b2 |
(8.4) |
|
а |
a 2 |
|||||
|
|
|
|
Таким образом, эксцентриситет эллипса меньше 1, а эксцентриситет окружности равен 0 (т.к. b = а).
Эксцентриситет эллипса можно рассматривать как меру его
«вытянутости». Если полуоси эллипса а = |
b ( e 1) |
, то эллипс |
||||||||
трансформируется в окружность радиуса R = а = b |
с центром в |
|||||||||
начале координат. В другом предельном |
случае e 0 эллипс |
|||||||||
настолько вытянут, что напоминает отрезок. |
|
|
|
|||||||
Пример 8.1. Привести уравнение кривой к каноническому |
||||||||||
виду и построить линию, определяемую уравнением |
|
|||||||||
x2 4y2 4x 8y 4 0 . |
|
|||||||||
Решение. Выделяя полные квадраты , преобразуем левую |
||||||||||
часть уравнения. Имеем |
|
|
|
|
|
|
|
|
|
|
(x2 2 2x 4 4) 4( y2 2y 1 1) 4 0 ; |
|
|||||||||
(x 2)2 4( y 1)2 4 ; |
|
(x 2)2 |
|
( y 1)2 |
1 . |
|
||||
|
|
|
|
|
|
|||||
|
|
|
4 |
|
|
|
1 |
|
|
|
Вводя новые координаты X x 2,Y y 1, получаем |
||||||||||
|
X 2 |
|
Y 2 |
1. |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
4 |
1 |
|
|
|
|
|
|
||
67
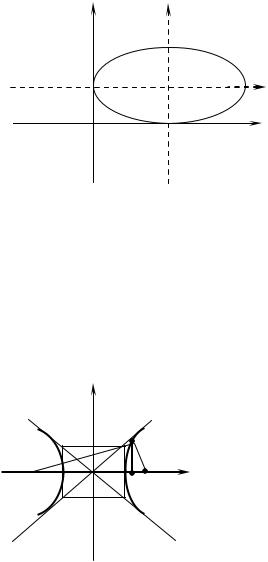
Таким образом получено уравнение эллипса с центром в точке О1 2;1 .
y Y
1 |
O1 |
X |
O |
2 |
x |
Рис. 15
8.2. Каноническое уравнение гиперболы
Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний
до двух фиксированных точек F1 ( с, о) и F2 (с, о) , называемых фокусами, есть величина постоянная 2a , меньшая, чем расстояние
между |
|
|
фокусами. |
|
Y |
|
|
|
|
M(x;y) |
|
r1 |
|
r2 |
X |
|
y |
||
|
|
|
|
F1(-c;0) |
0 |
x F2(c;0) |
|
Рис. 16
68

Согласно определению гиперболы можем записать для любой
точки гиперболы M (x, y) равенство |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(х с)2 у 2 |
|
(х с)2 у 2 |
2а; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a или 4cx 4a2 4a |
|
|
|
||||||||||
|
x c 2 y2 |
|
x c 2 |
y2 |
x c 2 |
y2 . |
||||||||||||
|
Обозначая b2 c2 |
a2 , имеем a2b2 |
b2 x2 |
a2 y 2 или |
|
|
||||||||||||
|
|
|
|
|
|
|
х2 |
|
|
у 2 |
1 |
, а b |
(8.5) |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
а 2 |
b2 |
|
|
|
|
|
|||||
- каноническое уравнение гиперболы.
Величины a и b называются соответственно действительной и мнимой полуосями гиперболы.
Так как x и y в уравнении в четных степенях, то график
гиперболы симметричен относительно координатных осей. Таким образом, гипербола обладает центром симметрии (как и эллипс).
Точки А(-а,0) и В(а, 0) называются вершины гиперболы и являются точками пересечения кривой с ось 0х . Фокусы гиперболы располагаются на действительной оси. Гипербола не пересекается с осью Oy .
Вводится основной прямоугольник гиперболы, образованный пересекающимися прямыми y b , y b , x a , x a . Диагонали основного прямоугольника гиперболы определяются
уравнениями |
y |
b |
x |
и |
y |
b x |
и являются асимптотами |
|
||||||
|
|
|||||||||||||
|
|
a |
|
|
|
a |
|
|
|
|
|
|
||
гиперболы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эксцентриситетом гиперболы называется величина |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
с |
|
|
1 |
b2 |
|
|
(8.6) |
|
|
|
|
|
|
|
a 2 |
|||||||
|
|
|
|
|
|
|
а |
|
|
|
||||
Таким образом, эксцентриситет гиперболы больше 1. Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины раствора угла между её асимптотами: чем
69
