
Курс лекций по линейной алгебре и аналитической геометрии. Горбунов В.В., Соколова О.А
.pdf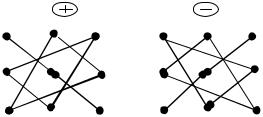
a |
a |
|
А= 11 |
12 |
|
|
|
|
a21 |
a22 |
|
ее определитель второго порядка вычисляется по формуле
det A= |
a11 |
a12 |
= |
a11a22 a12a21 , |
(2.1) |
a21 |
a22 |
т.е. из произведения элементов на главной диагонали вычитается произведение элементов на побочной диагонали.
Определитель третьего порядка вычисляется по формуле
|
a11 a12 a13 |
|
|
|
|
|
|
|
|
a21 |
a22 a23 |
a11 |
a22 |
a33 a21 a32 a13 a12 |
a23 |
a31 |
|
|
a31 |
a32 a33 |
|
|
|
|
|
(2.2) |
|
|
|
|
|
|
|
||
a13 a22 a31 a11 a23 |
a32 |
a12 a21 a33., |
|
|
|
|||
т.е. определитель третьего порядка равен алгебраической сумме шести тройных произведений элементов, стоящих в разных строках и разных столбцах; со знаком “плюс” берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников со стороной, параллельной главной диагонали; со знаком “минус” – произведения, сомножители которых стоят на побочной диагонали и в вершинах треугольников со сторонами, параллельными побочной диагонали (рис. 1).
а11 |
a12 |
а13 |
а11 |
|
а12 а13 |
а21 |
а22 |
а23 |
а21 |
а22 |
а23 |
а31 |
а32 |
а33 |
а31 |
а32 |
а33 |
Рис. 1
10
2.2.Основные свойства определителя
1.Величина определителя не меняется при транспонировании, т. е.
a11 a12 a13 |
|
a11 a21 a31 |
|
a21 a22 a23 |
= |
a12 a22 a32 |
. |
a31 a32 a33 |
|
a13 a23 a33 |
|
2.Перестановка двух строк (или двух столбцов) определителя равносильна умножению его на число (-1).
3.Если определитель имеет две одинаковые строки (или столбца), то он равен нулю.
4.Умножение всех элементов некоторой строки (столбца)
определителя на число равносильно умножению определителя на это число , т. е. общий множитель всех элементов некоторой строки (столбца) определителя можно выносить за знак определителя:
|
a11 a12 |
|
|
|
a11 |
a12 |
|
= |
|
a11 a12 |
|
. |
|
|
|
|
|
|
|||||||
|
a21 a22 |
|
|
|
a21 |
a22 |
|
|
|
a21 a22 |
|
|
5.Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.
6.Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.
7.Если каждый элемент n-ой строки (столбца) представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы определителей, первый из которых имеет в n-ой строке (столбце) первые из упомянутых слагаемых ), а второй определитель имеет в n-ой строке (столбце) вторые из упомянутых слагаемых. Остальные строки (столбцы) в исходном и полученных определителях не претерпели изменения:
|
a |
a |
... a |
a |
|
|
|
a |
... |
a |
|
|
|
a |
... a |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
11 |
11 |
|
1n |
1n |
|
|
|
11 |
|
1n |
|
|
|
11 |
1n |
|
|
|
|
a21 |
... |
a2n |
|
|
= |
|
a21 ... a2n |
|
+ |
|
a21 ... a2n |
|
. |
|||
|
|
an1 |
... |
ann |
|
|
|
|
an1 |
... |
ann |
|
|
|
an1 |
... ann |
|
|
8. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки
11

(столбца), умноженные на произвольный множитель , то величина определителя не изменится.
|
a11 a21 ... a1n a2n |
|
a11 ... a1n |
|
a21 |
... a2n |
|
|
|
|
|
||||
|
a21 ... a2n |
= |
a21 ... a2n |
+ |
a21 |
... a2n |
, |
|
an1 ... ann |
|
an1 ... ann |
|
an1 |
... ann |
|
a21 ... a2n
a21 ... a2n =0.
an1 ... ann
Минором элемента aij определителя n-го порядка называется определитель (n-1)-го порядка M ij , получаемый из данного определителя путем вычеркивания тех строки и столбца, на пересечении которых стоит aij .
Алгебраическим дополнением любого элемента аij
определителя называется число Аij , равное минору этого элемента,
взятому со знаком (+), если сумма номеров строки и столбца элемента есть число четное, и со знаком (-) – в противном случае
A ( 1)i j M |
ij |
, |
(2.3) |
ij |
|
|
|
например, |
|
|
|
|
1 |
0 |
3 |
|
|
|
|
|
|
|
|
|
2 4 1 |
; |
A |
4 |
1 |
; A |
2 1 |
. |
|||
|
|
|
|
|
11 |
2 |
7 |
12 |
5 |
7 |
|
|
5 |
2 |
7 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
9. Разложение определителя по строке (столбцу). (Один из способов вычисления определителя) Сумма произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения элементов этой строки (столбца) равна величине этого определителя.
Определитель 3-го порядка разложим по первой строке
a11 a12 a13 |
|
|
a22 a23 |
|
|
a21 a23 |
|
|
a21 a22 |
|
|||||
|
|
|
|
|
|
|
|||||||||
a |
|
a |
|
a |
|
= |
a |
- |
a |
+ |
a |
; |
|||
21 |
22 |
23 |
|
|
|
||||||||||
|
|
|
|
11 |
a32 a33 |
|
12 |
a31 a33 |
|
13 |
a31 a32 |
|
|||
a31 a32 a33 |
|
|
|
|
|
|
|
|
|
|
|||||
12
Пример 2.1. Вычислить определитель четвертого порядка
|
1 |
2 |
4 |
7 |
|
|
0 |
3 |
0 |
2 |
. |
|
2 |
4 |
3 |
2 |
|
|
6 |
3 |
1 |
1 |
|
|
|
|
|
|
|
Разложить определитель можно по любой строке (столбцу). Однако объем вычислений можно существенно уменьшить, если выбрать такую строку (столбец), в которой больше элементов, равных нулю. Наиболее подходящей в нашем случае является вторая строка. Разложение по ней определителя имеет вид
|
|
|
|
1 |
4 |
7 |
|
1 |
2 |
4 |
|
0A 3A 0A 2A 3( 1)4 |
2 |
3 |
2 |
2( 1)6 |
2 |
4 3 |
= |
||||
21 |
22 |
23 |
24 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
1 |
1 |
|
6 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
=3(3 +14 + 48 – 126 – 2 - 8) + 2(4 + 24 + 36 - 48 - 9 - 4)= -207.
10. Свойство ортогональности: сумма произведений
элементов aij некоторой |
|
строки |
(столбца) |
определителя на |
|
соответствующее алгебраическое |
дополнение |
другой строки |
|||
(столбца) равна нулю. |
|
|
|
|
|
2.3. Ранг матрицы |
|
||||
Пусть дана матрица, содержащая m строк и n столбцов |
|||||
|
a |
a ... a |
|
|
|
|
11 12 |
1n |
|
|
|
А = |
a |
21 a22 ... a2n |
|
(2.4) |
|
|
|
|
. |
||
|
... ... ... ... |
|
|
||
|
|
|
|
|
|
|
am1 am2 |
... amn |
|
||
Выделим в ней произвольным образом k строк и k столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка; определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что в общем случае таких миноров k-го порядка может быть несколько. При этом максимальный порядок миноров равен минимальному из чисел m и n, т. е.
max k = min(m,n).
13
Из всех возможных миноров матрицы А выделим те из них, которые отличны от нуля. В свою очередь, среди этих миноров можно найти, по крайней мере, один минор наибольшего порядка. Наибольший порядок минора, отличного от нуля, называется
рангом матрицы (2.4).
2.4.Вычисление ранга матрицы приведением
еек ступенчатому виду
Ранг матрицы А удобно вычислять с помощью элементарных преобразований:
Прибавление к одной строке другой строки, умноженной на число.
Перемена местами строк, столбцов.
Умножение всех элементов какой-либо строки (столбца) на число 0 .
При выполнении элементарных преобразований на каждом этапе происходит переход к новой матрице, однако, у всей цепочке матриц ранг матрицы одинаков. При выполнении элементарных преобразований нельзя пользоваться знаком равенства.
В результате элементарных преобразований получается ступенчатая матрица. Ранг ступенчатой матрицы равен числу ненулевых строк. Приведение матрицы к ступенчатому виду начинается с получения нулей в первом столбце под элементом
a11 . Для получения этого, если |
a11 0 , |
то |
умножаем первую |
|||
строку на число ( a21 / a11 ) |
и |
прибавляем ее ко 2-ой строке, |
||||
умножаем первую строку на число ( a31 / a11) |
и прибавляем ее к |
|||||
3-ей строке, и т.д. Тогда матрица примет вид: |
|
|||||
a |
a |
a |
a |
|
||
|
11 |
12 |
13 |
14 |
|
|
|
0 |
b22 |
b23 |
b24 |
|
|
|
0 |
b |
b |
b |
. |
|
|
|
|||||
|
32 |
33 |
34 |
|||
|
0 |
b42 |
b43 |
b44 |
|
|
|
|
|||||
Рассмотрим матрицу B 
 bij
bij 
 , образованную из полученной
, образованную из полученной
матрицы вычеркиванием первого столбца и первой строки элементами 2-й, ..., n-й строк и столбцов. Добьемся того, чтобы
14
b11 0 , переставляя местами строки. Если этого сделать нельзя, то
матрица уже имеет ступенчатый вид. Проделаем те же операции, что и с матрицей А, и так до тех пор, пока матрица не примет вид
a |
a |
a |
a |
... a |
|
|
|
|
11 12 13 |
14 |
1n |
|
|
||
0 |
a22 a23 |
a24 |
... a2n |
|
|||
|
|
|
|
|
|
|
|
|
0 |
0 |
a33 |
a34 ... a3n |
(2.5) |
||
... ... ... |
... ... ... |
|
|
||||
|
0 |
0 |
0 |
0 |
... 0 |
|
|
|
|
|
|||||
Пример 2.2. Найти ранг матрицы
1 |
3 |
2 |
|
|
А= |
2 |
1 |
0 |
. |
|
4 |
- 1 |
5 |
|
|
|
|||
Решение. Приведем матрицу к ступенчатому виду:
1 |
1 1 |
1 |
3 2 |
|
1 |
3 2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
- 3 4 |
|
|
0 - 5 2 |
|
|
0 |
- 5 |
2 |
. |
|
|
|
|
|
|
0 -15 6 |
|
|
0 |
0 |
0 |
|
|
|
4 -11 10 |
|
|
|
|
|||||||
1.Умножим каждый элемент 1-ой строки на (-2) и сложим со второй строкой; на (-4) и сложим с третьей строкой .
2.Умножим каждый элемент 2-ой строки на (-3) и сложим
с3-ей строкой.
3.Нетрудно увидеть, что максимальный порядок миноров этой матрицы отличных от нуля равен двум, поскольку минор третьего порядка содержит элементы 3-ей строки, которые равны нулю, следовательно, определитель третьего порядка равен нулю, таким образом r(A) = 2.
2.5. Вычисление обратной матрицы
Пусть дана невырожденная матрица n-го порядка
15
a |
a |
... a |
|
|
|
11 |
12 |
1n |
|
|
|
a21 a22 |
... a2n |
, |
(2.6) |
||
А = |
|
|
|
||
... ... ... ... |
|
|
|
||
|
|
|
|
|
|
an1 an2 |
... ann |
|
|
||
т. е. ее определитель |
не равен |
нулю. Рассмотрим |
~ |
составленную |
из алгебраических |
присоединенную матрицу A , |
||
дополнений к элементам матрицы А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
A |
|
... A |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
12 |
1n |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
~ A21 A22 ... A2n |
|
|
|
|
|
|
|
(2.7) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
А = |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
... ... ... ... |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
An2 ... Ann |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
An1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
После |
|
|
транспонирования |
|
присоединенной |
|
|
|
|
~ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
матрицы A |
|||||||||||||||||||||||||
вычисляем обратную матрицу A 1 по формуле |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
~ T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A 1 |
|
|
|
|
|
|
A . |
|
|
|
|
|
|
|
(2.8) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 2.3. |
Дана |
матрица |
|
А |
4 |
1 |
2 |
. |
Вычислить |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
8 |
6 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
обратную матрицу А 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Решение. Вычислим определитель матрицы |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
3 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
4 |
|
|
1 |
|
2 |
2 10 3 14 0 22 0. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
5 |
|
|
8 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Найдем алгебраические дополнения матрицы: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
А |
|
|
1 |
2 |
|
10; |
А |
|
|
4 |
2 |
|
14; |
|
А |
|
|
|
3 |
0 |
|
6; |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
11 |
|
|
|
8 |
6 |
|
|
|
|
12 |
|
|
|
5 |
6 |
|
|
|
|
|
13 |
|
|
|
1 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
2 |
0 |
|
|
|
|
|
|
2 |
0 |
|
|||||||||||||||
А |
|
3 |
|
|
18; |
А |
|
|
12; |
|
А |
|
|
4; |
|||||||||||||||||||
21 |
|
|
|
|
8 |
|
6 |
|
|
22 |
|
5 |
6 |
|
|
|
|
|
|
23 |
|
|
|
4 |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
3 |
|
|
0 |
6; |
А |
|
2 |
|
0 |
|
4; А |
|
|
|
2 |
3 |
14. |
||||||||||||||
|
31 |
|
1 |
|
2 |
|
32 |
|
4 |
|
2 |
|
|
|
|
|
33 |
|
|
|
|
4 |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
9 |
|
|
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
10 18 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
11 |
11 |
|
|
|
11 |
|
|
||||||||||||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
6 |
|
|
|
2 |
|
|
|
|
|
|||||
А |
|
|
|
|
|
14 12 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||
|
22 |
11 |
11 |
|
11 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
6 |
4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
14 |
|
|
|
3 |
|
|
2 |
|
|
|
|
7 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
11 |
|
|
11 |
|
|
|||||||||||
Вопросы для самопроверки
1.Что называется определителем? Каковы основные свойства определителя?
2.Что называется минором и алгебраическим дополнением? Приведите примеры.
3.Каковы способы вычисления определителей? Приведите
примеры.
4.Что называется рангом матрицы? Как его можно найти?
5.Какая матрица называется обратной для данной матрицы? Как можно найти обратную матрицу?
3.СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ
УРАВНЕНИЙ
3.1. Матричная форма системы уравнений
Система m линейных уравнений с n неизвестными (переменными) x1, x2 , ..., xn имеет вид
a11 x1 a12 x2 ... |
a1n xn b1 , |
|
|
||||||||||
|
|
|
|
|
|
|
a2n xn b2 |
|
|
||||
a21 x1 a22 x2 |
, |
(3.1) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
......... |
|
......... |
|
......... |
|
|
......... |
. |
...... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
m1 |
x a |
m2 |
x |
2 |
... |
a |
mn |
x |
n |
b |
m |
. |
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
Здесь aij - коэффициенты при неизвестных, и b j - свободные
члены системы уравнений (3.1).
Решением системы уравнений (3.1) называется набор n чисел x1 1, x2 2 , ..., xn n , при подстановке которых в эту систему
каждое уравнение данной системы превращается в верное равенство.
Система уравнений(3.1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной. Совместная система уравнений имеет либо одно решение, и в таком случае она называется определенной, либо, если у нее больше одного решения, она называется
неопределенной.
Системы уравнений вида (3.1) называются эквивалентными, если они имеют одно и то же множество решений.
Введем матрицу коэффициенты при неизвестных
a |
a |
... a |
|
|
|
11 |
12 |
1n |
|
|
|
a21 |
a22 ... a2n |
|
, |
(3.2) |
|
А = |
|
|
|
||
... |
... ... ... |
|
|
|
|
|
|
|
|
|
|
am1 |
am2 ... amn |
|
|
||
которая называется матрицей системы, а также матрицу-столбец неизвестных Х и матрицу свободных членов В:
x |
|
|
b |
|
|
|||
|
1 |
|
|
|
1 |
|
|
|
x2 |
|
|
b2 |
|
|
|||
A= |
|
|
, B= |
|
. |
(3.3) |
||
|
|
|
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
xn |
|
|
bm |
|
||||
Тогда систему линейных уравнений (3.1) можно записать в |
||||||||
матричной форме: |
|
|
|
|
|
|
|
|
АХ=В. |
|
|
|
(3.4) |
||||
Введем в рассмотрение |
|
расширенную матрицу |
системы |
|||||
A / B , дополним матрицу системы А столбцом свободных:
18
|
a |
a |
... |
a |
b |
|
|
|
11 |
12 |
|
1n |
1 |
|
|
|
a21 |
a22 |
... |
a2n |
b2 |
|
|
A / B |
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
... ... ... ... |
|
|
||||
|
|
|
|
|
|
|
|
|
am1 |
am2 |
... |
amn |
bm |
. |
|
|
|
|
|
|
|
|
|
Теорема 3.2. |
(теорема Кронекера-Капелли; критерий |
||||||
совместности системы). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.
3.2.Матричный метод решения системы уравнений
Рассмотрим систему вида
a11x1 a12 x2 |
... a1n xn |
b1 , |
|
||||||||||||
|
|
|
a22 x2 |
... a2n xn |
b2 , |
|
|||||||||
a21x1 |
|
||||||||||||||
..............................................., . |
(3.5) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
n1 |
x |
a |
n2 |
x |
2 |
... a |
nn |
x |
n |
b . |
|
|||
|
1 |
|
|
|
|
|
|
n |
|
||||||
В матричной форме система уравнений (3.5) имеет вид : |
|
||||||||||||||
|
|
|
|
|
|
АХ=В, |
|
|
|
|
|
|
|||
причем матрица системы |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
a |
|
a |
... a |
|
|
|
|
|
|||
|
|
|
|
|
11 |
|
12 |
1n |
|
|
|
|
|
||
|
|
A |
a21 |
a22 ... a2n |
|
|
|
(3.6) |
|||||||
|
|
|
|
|
... ... ... |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
... |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1 |
an2 ... ann |
|
|
|
|||||||
должна быть невырожденной, т.е. иметь определитель, отличный от руля. Умножив обе части матричного уравнения слева на A 1 ,
получаем решение системы (3.5) в матричной форме: |
|
X A 1B. |
(3.7) |
Вычисление обратной матрицы по заданной матрице А |
|
производится по формулам (2.3) и (2.8). |
|
Пример 3.1. Решить систему уравнений |
с помощью |
обратной матрицы |
|
19 |
|
