
2190
.pdfV abh max;
2k (ab (a b)h ) C зад ; a, b, h 0.
В этой постановке требуется определить размеры бака a,b,h, стоимость которого не должна превышать Cзад, чтобы его объем V был максимальным. Для решения задачи принимаем следующие значения:
K= 10 т. р/м2, Сзад=100 т.р.
Тогда математическая модель примет вид:
V |
abh |
|
max; |
|
|
20 |
(ab |
|
(a |
b ) h ) |
100 ; |
a , b , h |
0 . |
|
|
||
Решим данную задачу с использованием средств
EXCEL.
Решение задачи нелинейного программирования отличается от решения задачи линейного программирования следующим:
- назначаются начальные значения искомых перемен-
ных xj0
- в окне Параметры поиска решения не надо вводить Линейная модель.
Начальные значения xj0 желательно назначать близкими к ожидаемым оптимальным значениям, что ускорит решение задачи. Обязательным является требование к целевой функции которая в начальной точке должна быть не равна нулю (иначе возможно деление на ноль при вычислении Fk).
Необходимо сделать форму для ввода условий задачи (рис. 49), в которую далее вводятся
-зависимости для объема и стоимости (ячейки С8, С9);
-начальные значения xj0 (ячейки В3, С3, D3). В данном случае в качестве начальных значений выбираются единичные;
140
-значение правой части ограничения (ячейка E9).
Вячейках, в которых будет представлен результат (B3:D3), перед решением задачи надо назначить число знаков после запятой. В нашем примере назначаем в ячейках 2 знака после запятой.
|
|
ПЕРЕМЕННЫЕ |
|
|
|
a |
b |
h |
|
значения |
1 |
1 |
|
1 |
нижн. гр |
|
ЗАВИСИМОСТИ |
|
|
|
|
|
|
|
|
обозначение |
величина |
знак |
правая часть |
объем |
V |
=B3^C3^D3 |
макс |
|
стоимость C |
=20^(B3^C3+(B3+C3)^D3) |
<= |
100 |
|
Рис. 49
Далее вызывается программа Поиск решения и в появившемся диалоговом окне вводится ячейка для целевой функции (С8), направление поиска (максимизация), изменяемые ячейки (B3:D3). Затем выбирается пункт Добавить и в появившемся окне Добавление ограничений вводятся огра-
ничения B3>=B4; C3>=C4; D3>=D4, C9<=E9. После ввода всех ограничений в окне поиска решения выбирается команда Параметры и осуществляется переход в диалоговое окно Параметры поиска решения. В нем назначаются параметры поиска решения.
Следует отметить, что при поиске оптимального решения смысл этих параметров знать необязательно, так как их значения, применяемые по умолчанию, обеспечивают нормальное решение практических задач. В противном случае все сведения можно получить вызвав Справку.
После ввода всех исходных данных и параметров производится решение задачи. Результаты решения представлены на рис. 50.
141
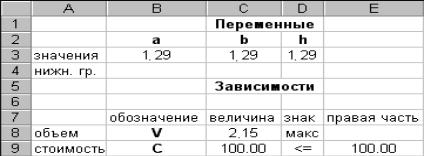
Рис. 50 После успешного завершения поиска оптимального ре-
шения на экране появляется диалоговое окно Результаты поиска решения. С помощью этого диалогового окна можно вы-
звать отчеты трех типов: результаты, устойчивость и преде-
лы. Отчеты анализа по результатам и пределам аналогичны таким же отчетам для задач линейного программирования. Отчет по устойчивости представлен на рис. 51. и состоит из двух таблиц.
Изменяемые ячейки |
Результат |
Нормир. |
|
|
|
||
Ячейка |
Имя |
значение |
градиент |
$B$4 |
значения а 1.29 |
0.00 |
|
$C$4 |
значения b 1.29 |
0.00 |
|
$D$4 |
значения h 1.29 |
0.00 |
|
Ограничения |
Результ. |
Лагранжа |
|
|
|
||
Ячейка |
Имя |
значение |
Множитель |
$C$10 |
С величина 100.00 |
0.03 |
|
|
|
Рис. 51 |
|
В первой таблице приводятся значения для перемен-
ных:
результат решения задачи; 142

-нормированный градиент - величина, приводимая при выборе некоторых методов в диалоговом окне Параметры поиска решения;
Во второй таблице приводятся значения для ограниче-
ний:
-величина стоимости;
-множитель Лагранжа, показывающий, как изменится целевая функция при изменении правой части в ограничении на единицу.
Для задач линейного программирования можно произвести также параметрический анализ, решая их при различных значениях параметров. Алгоритм выполнения параметрических расчетов аналогичен схеме, рассмотренной при решении задач линейного программирования, поэтому в данном разделе разбираться не будет. На рис. 52. приведен итоговый сценарий, построенный в результате решения рассматриваемой задачи нелинейного программирования при различных значениях стоимости: 100, 200, 300, 400, 500 [4].
ИТОГОВЫЙ СЦЕНАРИЙ |
|
|
|
|
|
|
|
Текущие значения с=100 |
с=200 |
с=300 |
с=400 |
с=500 |
|
Изменяемые ячейки |
|
|
|
|
|
|
$B$4 |
2.89 |
1.29 |
1.83 |
2.24 |
2.58 |
2.89 |
$C$4 |
2.89 |
1.29 |
1.83 |
2.24 |
2.58 |
2.89 |
$D$4 |
2.89 |
1.29 |
1.83 |
2.24 |
2.58 |
2.89 |
Ячейкирезультата |
|
|
|
|
|
|
$C$9 |
24.06 |
2.15 |
6.09 |
11.18 |
17.21 |
24.06 |
$C$10 |
500.00 |
100.00 |
200.00 |
300.00 |
400.00 |
500.00 |
Примечание: в столбце Текущие значения приведены данные в изменяемыхячейкахна момент создания отчета Итоговый сценарий.
Рис. 52
Решение нелинейных целочисленных задач
Решение целочисленных задач нелинейного программирования производится аналогично решению обычных нелинейных задач, но с наложением дополнительного требования целочисленности переменных. Решение таких задач рассмот-
143
рим на примере рассматриваемой задачи определения параметров бака максимального объема, потребовав, чтобы все параметры бака принимали целочисленные значения.
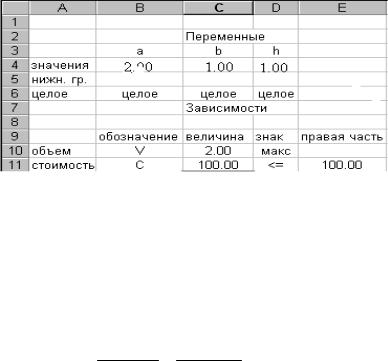
Таблица исходных данных при переходе от непрерывной задачи к целочисленной не меняется (рис. 49). Дальнейшая последовательность ввода исходных данных совпадает с последовательностью, рассмотренной для непрерывной задачи. Однако при добавлении ограничений к введенным ранее ограничениям необходимо добавить требования целочисленности: В4, С4 и D4 целое. Результат решения представлен на рис. 53.
Рис. 53
Из всех отчетов по анализу оптимального решения для рассматриваемых целочисленных задач может быть получен только один Отчет по результатам. В нем нет какой-либо новой информации, поэтому рассматривать его не имеет смысла.
Сравнив результаты решения непрерывной и целочисленной задач, мож-но вычислить показатель ухудшения значения целевой функции
fнепр fц 2.15 2.0 6.98.
fнепр 2.15
144
Решение нелинейных задач дискретного программирования
Под задачей дискретного программирования будем понимать задачу, в которой переменные могут принимать не любые значения, а только те, которые входят в заданный набор дискретных допустимых значений. При этом задаваемые значения могут быть любыми, в том числе и не целочисленными.
Задачу дискретного программирования проиллюстрируем на примере поиска оптимальных размеров бака при дополнительном условии, что сторона “а” может принимать любое значение из заданных: 4,25; 5,5; 6,75.
Математическая модель задачи, рассмотренная выше, дополнится следующими условиями:
a 4,25 1 |
5,5 2 6,75 3 |
0 |
(a) |
|||
1 2 3 |
1 |
|
|
|||
|
(b) |
|||||
0 j 1; |
|
j целое |
|
|
||
|
|
|
||||
|
|
|
|
|
|
|
j 1,3 |
|
|
|
|||
|
|
|
|
|||
Форма для ввода исходных данных при этом дополняется (рис. 54)
-столбцами для ввода булевых переменных 1, 2, 3; (на рисунке d1, d2,d3);
-строкой для верхних границ;
-строкой с указанием требований целочисленности (данная строка является необязательной);
-строками, соответствующими ограничениям (а) и (b).
145
|
|
П ерем енны е |
|
|
|
|
|
|
|
a |
b |
h |
d1 |
|
d2 |
|
d3 |
значения |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
нижн. гр. |
|
|
|
|
0 |
|
0 |
0 |
верх. гр. |
|
|
|
|
1 |
|
1 |
1 |
целое |
|
|
|
целое |
|
целое |
|
целое |
|
|
З ависим ости |
лев. часть знак |
|
прав.часть |
|||
|
|
|
|
|
||||
V |
|
|
|
|
1 |
макс |
|
|
C |
|
|
|
|
|
<= |
|
100 |
огр(а) |
-4.25 |
-5.5 |
-6.75 |
-3.25 |
|
= |
|
0 |
огр(b) |
|
1 |
1 |
1 |
3 |
= |
|
1 |
Рис. 54
Вячейки E13 и E14 вводятся зависимости для дополнительных ограничений:
(а) - в Е13=В4-В13*Е4-С13*F4-D13*G4,
(b)- в Е14=Е4+F4+G4.
Вячейки G13, G14 вводятся правые части ограничений.
Начальные приближения для переменных 1, 2, 3 (единичные) вводятся в ячейки (E4-G4).
В диалоговом окне Поиск решения вводится:
-направление поиска - максимизация;
-целевая ячейка - Е11;
-изменяемые ячейки B4:G4;
-граничные условия для xj:
B4>=B5; C4>=C5; D4>=D5;
-граничные условия для j: E4>=E5; E4<=E6; E4 - целое; F4>=F5; F4<=F6; F4 - целое; G4>=G5; G4<=G6; G4 - целое;
-ограничения:
E12<=G12;
E13=G13;
E14=G14.
146
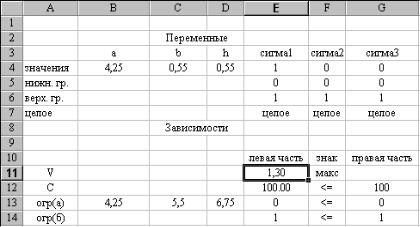
Результаты решения представлены на рис. 55. При этом значение целевой функции ухудшилось.
Рис. 55
Сравнительный результат параметрирования для непрерывной задачи и задачи дискретного программирования приведен на рис. 56.
И тоговы й сценарий |
|
|
|
|
|
|
|
с = 100 |
с = 200 |
с = 300 |
с = 400 |
с =500 |
|
a |
4.25 |
4.25 |
4 |
.25 |
4.25 |
4.25 |
b |
0.55 |
1.05 |
1 |
.50 |
1.92 |
2.31 |
h |
0.55 |
1.05 |
1 |
.50 |
1.92 |
2.31 |
об ъ ем д иск р. |
1.30 |
4.66 |
9 |
.56 |
15.66 |
22.72 |
об ъ ем непрер. |
2.15 |
6.09 |
1 |
1.18 |
17.21 |
24.06 |
V д /V н |
0.60 |
0.77 |
0 |
.86 |
0.91 |
0.94 |
Рис. 56
Из приведенных данных видно, что дополнительное требование дискретного программирования в задаче о баке уменьшает величину объема для баков различной стоимости.
147
ЛЕКЦИЯ 14 МЕТОД АНАЛИЗА ИЕРАРХИЙ
Во многих задачах управления сложными процессами и объектами приходится сталкиваться с проблемой принятия решений при выполнении операций в условиях неопределенности. Неопределенными могут быть как условия выполнения операции, так и сознательные действия конкурентов или других лиц, от которых зависит успех операции. Кроме того, неопределенность в той или иной степени может относиться также и к целям (задачам) операции, успех которой далеко не всегда может быть исчерпывающим образом охарактеризован одним единственным числом – интегральным показателем эффективности. В машиностроении подобные ситуации возникают при планировании развития производства, рассмотрении альтернативных вариантов выбора технологий, оборудования, материала, анализе эффективности работы.
К числу наиболее эффективных методов принятия решений в сложных ситуациях относится метод анализа иерархий (МАИ), предложенный американским ученым Т. Саати. Данный метод опирается на декомпозицию сложной проблемы, на ее более простые составляющие части и дальнейшую математическую обработку (моделирование) последовательности суждений лиц, принимающих решения (ЛПР), которые формируются в виде совокупности парных сравнений.
В рамках МАИ на первом этапе решения проблемы образуется доминантная иерархия, формируемой начиная с вершины (цели – с точки зрения управления), через промежуточные уровни (критерии или факторы, от которых зависят последующие уровни) к самому нижнему уровню (который обычно определяет перечень альтернатив, подлежащих выбору). Иерархия считается полной, если каждый элемент заданного уровня функционирует как критерий для всех элементов нижестоящего уровня.
Рассмотрим простой пример, наглядно иллюстрирующий формирование иерархии при реализации МАИ.
148
Директору предприятия необходимо купить оборудование для своего предприятия (цель управления). В результате обсуждения удалось определить восемь критериев, уточняющих цель, которым, должно удовлетворять оборудование. Задача заключается в выборе одного из трех станков (альтернативы). Соответствующая нисходящая иерархическая декомпозиция представлена на рис. 57.
После иерархического воспроизведения проблемы реализуется второй этап – установления приоритетов для критериев и оценка альтернатив в соответствии с принципом дискриминации и сравнительных суждений. Проводится опрос лиц принимающих решения (ЛПР) или экспертов. В МАИ элементы проблемы сравниваются попарно по отношению к их воздействию («весу», «интенсивности») на общую для них характеристику. Очевидно, что установление важности элементов при попарном сравнении есть отражение способности человека к высказыванию относительных (сравнительных) суждений притом, что он обычно затрудняется сразу оценить многоаспектную проблему в целом.
Другой пример выстраивания иерархии для решения сложной проблемы представлен на рис. 58.
Пусть A1,...,An – множество n элементов некоторого уровня иерархии и 1,..., n абсолютные веса или интенсивно-
сти этих элементов, которые нам неизвестны заранее. В рамках МАИ с участием ЛПР формируется матрица попарных сравнений элементов на основе субъективных суждений, численно оцениваемых по определенной шкале. На основе выраженных численно результатов попарных сравнений потом решается задача нахождения абсолютных весов. В идеале, при полной согласованности суждений матрица попарных сравнений имеет вид рис.59.
149
