Модель многоотраслевой экономики (балансовый метод или модель Леонтьева)

Каждая отрасль производства производит продукцию ипотребляет как продукцию других отраслей, так и свою собственную.

Задача: Найти объем производства каждой изотраслей, который удовлетворит все потребности всех отраслей и конечного потребителя.

Математическая модель и решение этой задачи были разработана В. Леонтьевым.

Пусть

- валовой объем продукции -той отрасли,

- объем продукции-той отрасли, потребляемой-той отраслью,

- объем продукции -той отрасли для непроизводственного потребления.

–-тая отрасль.

Если мы рассматриваем отраслей, то, и соотношения баланса можно представить в виде уравнений:

(1)

Пусть все величины в (1) имеют стоимостное выражение (в рублях например). Тогда можно ввести так нназываемые коэффициенты прямых затрат:

,

которые показывают затраты продукции -той отрасли на один рубль производства-той отрасли.

Считается, что зависят от технологии производства и поэтому постоянны на некотором интервале времени. Это предположение означает линейную зависимость материальных средств от валового выпуска:

.

Такую модель многоотраслевого баланса называют линейной:

.

Пусть

, ,,

где — матрица-столбец валового выпуска;— матрица прямых затрат (технологическаяили структурная матрица);- матрица конечного продукта.

В этих обозначениях уравнения межотраслевого баланса имеют вид:

(2)

Теперь основную задачу межотраслевого баланса можно сформулировать следующим образом:

Найти матрицу , которая обеспечит выпуск конечного продукта, заданного матрицей, при известной матрице прямых затрат.

Перепишем (2) в виде:

,

и если — невырождена, то найдем решение с помощью обратной матрицы:

(4)

Матрицу называютматрицей полных затрат. Каждый элементматрицыесть часть стоимости валового выпуска продукции-той отрасли, необходимая для выпуска продукта единичной стоимости-той отраслью. Для подтверждения этого вывода следует задать

, , … ,.

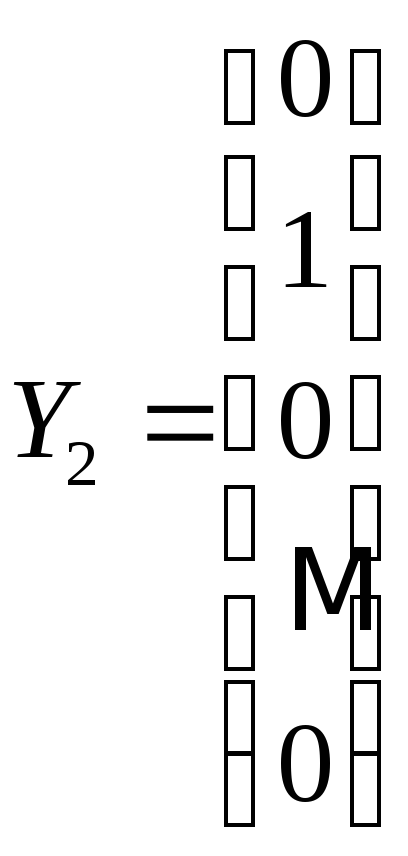При подстановке в уравнение (3), получим:

, ,.

В соответствии с экономическим смыслом задачи все элементы матриц ,,должны быть неотрицательны.

Неотрицательная матрица называетсяпродуктивной, если для любой неотрицательной матрицысуществует неотрицательное решение.

Критерий продуктивности. Матрицапродуктивна, если для ее элементоввыполняется неравенство

,

причем существует хотя бы одно значение , для которого

.

Существуют и другие критерии продуктивности матриц.

Многомерные вектора и векторные пространства

Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.

Арифметическим п-мерным вектором x называется упорядоченная совокупность п чисел, записываемых в виде x=(x₁,x₂,…,x_n), где x_i — компоненты векторах x.

Два п-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е.

x=у, если х_i=y_i , (i=1,2,...,n).

Для арифметических векторов вводятся две линейные операции:

Суммой двух векторов одинаковой размерности п называется вектор z=х+у компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. z_i=x_i+y_i, (i = 1,2,...,n).

Произведением вектора х на действительное число называется вектор и = х, компоненты u_i которого равны произведению на соответствующие компоненты вектора х, т.е.

если и = х, то u_i=x_i,, (i=1,2,...,n)

Полагается, что линейные операции над векторами подчиняются следующим аксиомам:

1. х+у=у+x — коммутативное свойство суммы;

2. (x+у)+z=x+(у+z) — ассоциативное свойство суммы;

3. (x)=()х — ассоциативное свойство относительно числового множителя;

4. (x+у)= х+у — дистрибутивное свойство относительно суммы векторов;

5. ()x = x + x — дистрибутивное относительно суммы числовых множителей свойство;

6. Существует нулевой вектор 0=(0, 0, ... , 0) такой, что x+0=х для любого вектора х;

7. Для любого вектора х существует противоположный ему вектор (–x) такой, что x+(–x)=0;

8. 1•х = х для любого вектора х .

Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведенным выше аксиомам, называют линейным векторным пространством.