
Московский государственный технический
университет им. Н.Э. Баумана.
Калужский филиал.
Т.С. Китаева, Р.В. Нехаенко
«Определение отношения молярных теплоёмкостей газа при
постоянном давлении и объёме по методу Клемана и Дезорма»
Методические указания к выполнению лабораторной работы № 7
по курсу механики, молекулярной физики и термодинамики.
Калуга 2007 г.
Целью настоящей
работы является определение отношения
молярных теплоёмкостей воздуха при
постоянном давлении и объёме
![]() по методу Клемана и Дезорма.
по методу Клемана и Дезорма.
1. Теоретическая часть.
Согласно первому закону (началу) термодинамики для бесконечно малого или элементарного квазистатического процесса:
![]() ,
(1)
,
(1)
где
![]() - элементарное количество теплоты,
сообщённое системе;
- элементарное количество теплоты,
сообщённое системе;
![]() - элементарная
работа, совершаемая системой против
внешних тел;
- элементарная
работа, совершаемая системой против
внешних тел;
![]() - элементарное
изменение внутренней энергии системы.
- элементарное
изменение внутренней энергии системы.
В качестве системы рассмотрим идеальный газ.
Величины
![]() и
и
![]() ,
в отличие от
,
в отличие от
![]() ,
не являются функциями состояния, а
зависят от способа перехода идеального
газа и будут неодинаковы в различных
процессах, в то время как величина
,
не являются функциями состояния, а
зависят от способа перехода идеального
газа и будут неодинаковы в различных
процессах, в то время как величина
![]() будет одна и та же.
будет одна и та же.
Величины, связанные первым законом термодинамики, могут быть вычислены независимо друг от друга. Рассмотрим одну из них.
По определению:
![]() ,
(2)
,
(2)
где
![]() - удельная теплоёмкость газа,
- удельная теплоёмкость газа,
![]() ;
;
или
![]() ,
(3)
,
(3)
где
![]() - молярная теплоёмкость газа,
- молярная теплоёмкость газа,
![]() ;
;
![]() - число молей
идеального газа,
- число молей
идеального газа,
![]() .
.
Приравняем (2) и (3), получим связь между теплоёмкостями;

 (4)
(4)
Наибольший интерес
представляет молярная теплоёмкость
газа при постоянном давлении (![]() )
и при постоянном объёме (
)
и при постоянном объёме (![]() ).
).
Отношение
 представляет собой характерную для
каждого газа величину, которую можно
рассчитать теоретически:
представляет собой характерную для
каждого газа величину, которую можно
рассчитать теоретически:
![]() ;
;
![]() ,
,
где
![]() - универсальная газовая постоянная,
численно равная
- универсальная газовая постоянная,
численно равная
![]() ;
;
![]() - число степеней
свободы молекулы, для одноатомных газов
- число степеней
свободы молекулы, для одноатомных газов
![]() ,
для двухатомных
,
для двухатомных
![]() ,
для трёхатомных и многоатомных
,
для трёхатомных и многоатомных
![]() .
.
Тогда
 (5)
(5)
Так для воздуха
(![]() )
имеем:
)
имеем:
![]() .
.
Число
![]() входит также в уравнение Пуассона,
связывающее давление и объём идеального
газа при адиабатическом процессе,
происходящем без теплового обмена с
окружающей средой, и называется
коэффициентом Пуассона или показателем
адиабаты.
входит также в уравнение Пуассона,
связывающее давление и объём идеального
газа при адиабатическом процессе,
происходящем без теплового обмена с
окружающей средой, и называется
коэффициентом Пуассона или показателем
адиабаты.
Запишем первый закон термодинамики в дифференциальной форме:
![]() ,
,
где
![]() ;
;
 ;
;
![]() ,
,
тогда
 (6)
(6)
Продифференцируем уравнение Менделеева-Клапейрона:
 ,
,
тогда
 ,
,
отсюда
 (7)
(7)
Подставим (7) в (6):
 .
.
Воспользуемся уравнением Майера:
![]() ,
(8)
,
(8)
тогда
![]() ,
,
или
![]() .
.
Поделим полученный
результат почленно на
![]() :
:
 ,
,
где
 ;
;
 (9)
(9)
В результате интегрирования и потенцирования (9) получим:
![]() ;
;
или
![]() (10)
(10)
Выражение (10) называют уравнением Пуассона, которое для двух произвольных состояний запишется так:
![]() (11)
(11)
Уравнение Пуассона используется при выводе экспериментальной формулы.
2. Экспериментальная часть.
Одним из методов
экспериментального определения
 является метод Клемана и Дезорма. Суть
его заключается в следующем. Стеклянный
баллон (сосуд) вместимостью в несколько
литров наполняется исследуемым газом
- воздухом, который при атмосферном
давлении и комнатной температуре по
своим свойствам приближается к идеальному.
Сосуд снабжён тремя трубками (Рис. 1.).
Первая (1) - широкая (для лучшего
адиабатического расширения воздуха,
находящегося в сосуде), соединена с
сосудом и запирается краном
является метод Клемана и Дезорма. Суть
его заключается в следующем. Стеклянный
баллон (сосуд) вместимостью в несколько
литров наполняется исследуемым газом
- воздухом, который при атмосферном
давлении и комнатной температуре по
своим свойствам приближается к идеальному.
Сосуд снабжён тремя трубками (Рис. 1.).
Первая (1) - широкая (для лучшего
адиабатического расширения воздуха,
находящегося в сосуде), соединена с
сосудом и запирается краном
![]() ;
вторая (2) – соединена с насосом и снабжена
краном
;
вторая (2) – соединена с насосом и снабжена
краном
![]() ;
третья (3) - соединена с U-образным
жидкостным (водяным) манометром (4).
;
третья (3) - соединена с U-образным
жидкостным (водяным) манометром (4).
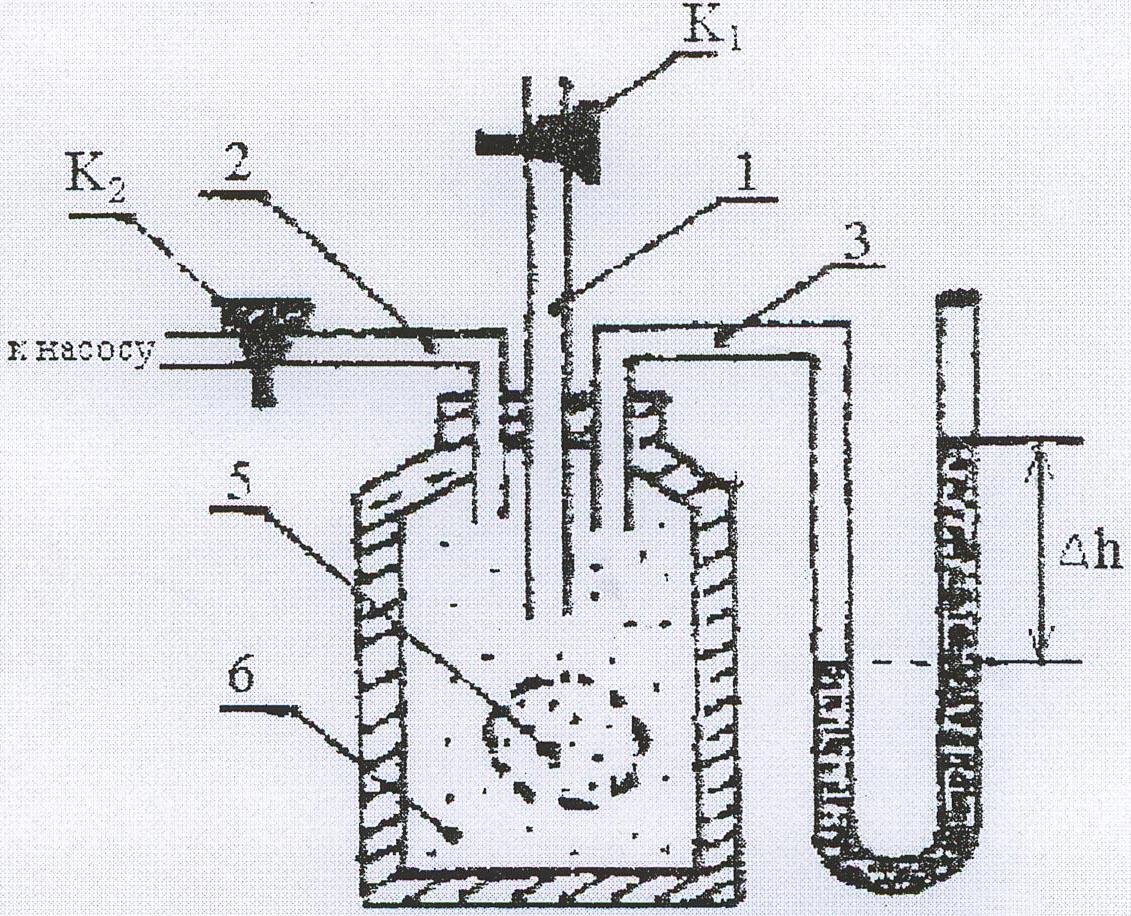
Рис. 1. Экспериментальная схема определения
 по методу Клемана
и Дезорма.
по методу Клемана
и Дезорма.
Мысленно выделим внутри баллона произвольную порцию газа, ограниченную замкнутой поверхностью, выполняющей роль «оболочки» (5). В различных процессах газ внутри «оболочки» будет расширяться и сжиматься, совершая работу против давления окружающего газа (6) и обмениваясь с ним теплотой. Поскольку кинетическая энергия возникающего макроскопического движения невелика, эти процессы могут рассматриваться как квазистатические.
Если отрыть кран
![]() ,
то параметры состояния мысленно
выделенного малого объёма воздуха будут
равны:
,
то параметры состояния мысленно
выделенного малого объёма воздуха будут
равны:
![]() ;
;
![]() ;
;
![]() ,
,
где
![]() - атмосферное давление;
- атмосферное давление;
![]() - температура
окружающей среды (комнатная).
- температура
окружающей среды (комнатная).
Если закрыть кран
![]() и, открыв кран
и, открыв кран
![]() ,
ведущий к насосу, накачать в сосуд
некоторое количество воздуха, а затем
закрыть кран
,
ведущий к насосу, накачать в сосуд
некоторое количество воздуха, а затем
закрыть кран
![]() ,
то рассматриваемый малый объём сожмётся,
а его температура и давление повысятся.
Через некоторое время, благодаря
теплообмену с окружающей средой,
температура воздуха в сосуде снова
сравняется с комнатной, а параметры
состояния воздуха в «оболочке» будут
равны:
,
то рассматриваемый малый объём сожмётся,
а его температура и давление повысятся.
Через некоторое время, благодаря
теплообмену с окружающей средой,
температура воздуха в сосуде снова
сравняется с комнатной, а параметры
состояния воздуха в «оболочке» будут
равны:
![]() ;
;
![]() ;
;
![]() ,
,
где
![]() - установившаяся разность уровней
жидкости в манометре.
- установившаяся разность уровней
жидкости в манометре.
Если на короткое
время открыть широкую трубку (кран
![]() ),
то воздух в сосуде адиабатически
расширится и вследствие этого охладится.
В конце этого малого промежутка времени,
когда широкая трубка открыта, давление
воздуха внутри сосуда сравняется с
атмосферным и состояние воздуха внутри
«оболочки» в данный момент определится
параметрами:
),
то воздух в сосуде адиабатически
расширится и вследствие этого охладится.
В конце этого малого промежутка времени,
когда широкая трубка открыта, давление
воздуха внутри сосуда сравняется с
атмосферным и состояние воздуха внутри
«оболочки» в данный момент определится
параметрами:
![]() ;
;
![]() ;
;
![]() ,
,
причём
![]() .
.
Когда давление в
сосуде сделается равным давлению
атмосферы (разность уровней жидкости
в манометре равна нулю), широкую трубку
закрывают (кран
![]() ).
Воздух, находящийся в сосуде, станет
нагреваться от
).
Воздух, находящийся в сосуде, станет
нагреваться от
![]() до
до
![]() за счёт теплообмена с окружающей средой.
Вследствие этого давление в сосуде
начнёт повышаться до величины
за счёт теплообмена с окружающей средой.
Вследствие этого давление в сосуде
начнёт повышаться до величины
![]() ,
где
,
где
![]() - установившаяся разность уровней
жидкости в манометре после выравнивания
температур. Параметры состояния малого
объёма воздуха равны:
- установившаяся разность уровней
жидкости в манометре после выравнивания
температур. Параметры состояния малого
объёма воздуха равны:
![]() ;
;
![]() ;
;
![]() .
.
Итак, для вывода экспериментальной расчётной формулы рассмотрим три состояния малого объёма воздуха в «оболочке»:
I состояние (после закачивания воздуха в сосуд и последующего его охлаждения до температуры окружающей среды), характеризуемое параметрами:
![]() ;
;
![]() ;
;
![]() .
.
II состояние (короткое, наступающее в конце адиабатного расширения) с параметрами:
![]() ;
;
![]() ;
;
![]() .
.
III состояние (в конце эксперимента), характеризуемое параметрами:
![]() ;
;
![]() ;
;
![]() .
.
Переход из I-го состояния во II-ое представляет собой адиабатный процесс. Согласно уравнению Пуассона, имеем:
![]() (12)
(12)
I-ое
и III-ее
состояния при
![]() связаны законом Бойля-Мариотта:
связаны законом Бойля-Мариотта:
![]() (13)
(13)
Возведём уравнение
(13) в степень
![]() :
:
![]() (14)
(14)
Поделив почленно уравнение (14) на (12), получим:
 ,
,
отсюда
 (15)
(15)
Взяв натуральный
логарифм левой и правой частей (15) и
решая относительно
![]() ,
находим:
,
находим:
 (16)
(16)
Принимая во
внимание, что
![]() ,
,
![]() ,
получим
,
получим
![]() ,
,
![]() .
.
Подставляя
полученные выражения для
![]() и
и
![]() в
равенство (16), имеем:
в
равенство (16), имеем:
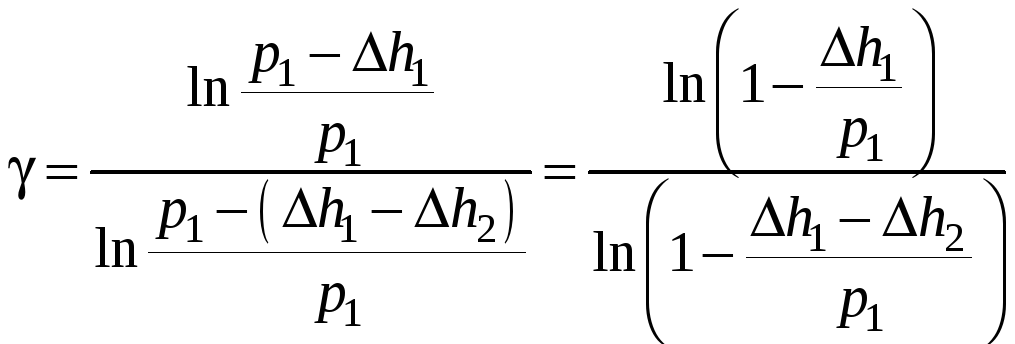 (17)
(17)
Так как
![]() и
и
![]() значительно меньше
значительно меньше
![]() ,
то числитель и знаменатель правой части
равенства (17) можно разложить в степенной
ряд, воспользовавшись формулой:
,
то числитель и знаменатель правой части
равенства (17) можно разложить в степенной
ряд, воспользовавшись формулой:

Ограничимся при разложении первой степенью. Тогда
для числителя:
 ;
;
для знаменателя:
 ;
;
окончательно:
 (18)
(18)
