10

Московский государственный технический

университет им. Н.Э. Баумана.

Калужский филиал.

Т.С. Китаева, р.В. Нехаенко «Определение коэффициента динамической вязкости воздуха»

Методические указания к выполнению лабораторной работы № 15

по курсу механики, молекулярной физики и термодинамики.

Калуга 2007 г.

Цель работы заключается в определении коэффициента динамической вязкости воздуха методом истечения воздуха через капилляр.

1. Теоретическая часть.

Термодинамическая система представляет собой совокупность макроскопических тел. Её состояние задаётся термодинамическими параметрами – параметрами состояния, в качестве которых обычно выбирают температуру, давление и удельный объём.

Термодинамическая система находится в равновесии, если её состояние с течением времени не меняется.

В термодинамических неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы и импульса.

К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса).

Механизм возникновения внутреннего трения между параллельными слоями газа, движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями. В результате импульс слоя, движущегося быстрее, уменьшается; движущегося медленнее - увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Сила внутреннего трения между двумя слоями газа подчиняется закону Ньютона:

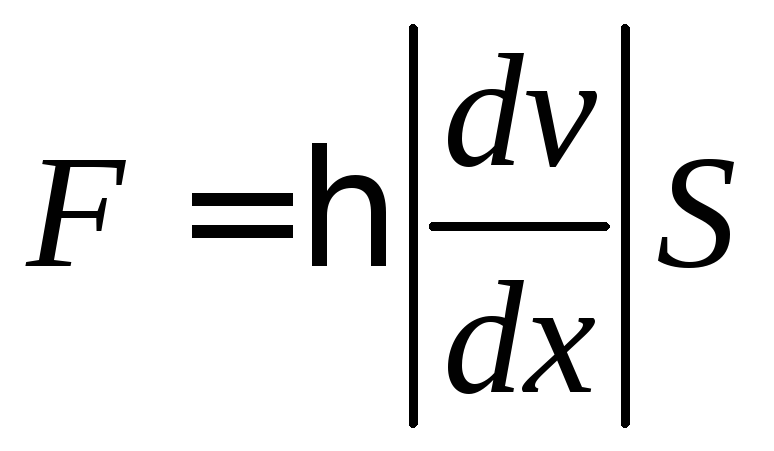, (1)

где - коэффициент динамической вязкости газа (динамическая вязкость),;

- модуль градиента скорости; показывает быстроту изменения скорости в направлении оси , перпендикулярном движению слоёв;

- площадь, на которую действует сила .

Взаимодействие двух слоёв согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передаётся импульс, по модулю равный действующей силе. Тогда выражение (1) можно переписать в виде:

, (2)

где - плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени через единичную площадку, перпендикулярную осив положительном направлении данной оси. Знак «минус» показывает, что импульс переносится в направлении убывания скорости.

Таким образом, динамическая вязкость численно равна плотности потока импульса при градиенте скорости, равном единице.

Можно показать, что:

, (3)

где - плотность газа;

- средняя арифметическая скорость теплового движения молекул;

- средняя длина свободного пробега молекул.

Согласно молекулярно-кинетической теории газов:

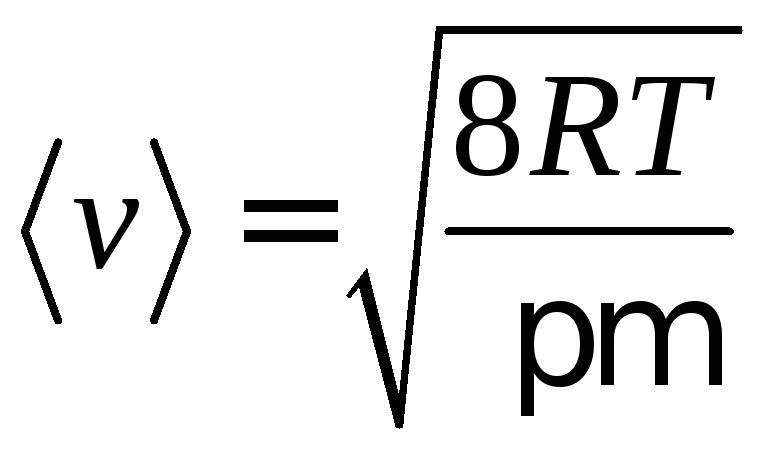, (4)

где - абсолютная температура газа;

- молярная масса газа;

- универсальная газовая постоянная.

Откуда следует, что с увеличением температуры увеличивается средняя арифметическая скорость теплового движения молекул, и динамическая вязкость в газах возрастает.

Наряду с коэффициентом динамической вязкости часто используется коэффициент кинематической вязкости :

, (5)

где - плотность газа.

Коэффициент кинематической вязкости в СИ измеряется в метрах квадратных на секунду, .