Способы вычисления углового ускорения

1. Графоаналитический

Для нахождения углового ускорения воспользуемся уравнением движения машинного агрегата в дифференциальной форме

При этом ,

где тангенс угла наклона касательной в каждой точке графика , значение производной подставляются в исходное уравнение с учетом знака.

2. Графический

Для нахождения углового ускорения воспользуемся кинематической зависимостью между угловой скоростью и ускорением:

При этом ,

где тангенс угла наклона касательной в каждой точке графика , значение производной подставляются в исходное уравнение с учетом знака.

Применение этой формулы приводит к большим погрешностям, так как она основывается на использовании одной из конечных зависимостей расчета . Кроме того, в точках с нулевыми значениямирасчет по этой формуле дает неверный результат.

Определение времени работы механизма (быстродействие механизма)

Чтобы найти закон движения начального звена, т.е. изменение кинематическихпараметров в функции времени, ее представляют в виде:, откуда после интегрирования получают. Найденная зависимость позволяет определить время работы механизма и найти искомую зависимость. Если функция получена в виде графика (Рис), то приходится проводить графическое интегрирование так называемой обратной функции.

Порядок графического интегрирования обратной функции:

1. Строят оси координат, в которых вычерчивают график . Определяют масштабыи.

2. Ось абсцисс делят на некоторое число шагов с равными или не равными интервалами. В пределах каждого интервала заданную функцию считают постоянной и равной среднему значению ординаты.

3. Концы ординат середины каждого интервала проецируют на ось, отмечая точки . Далее отрезкиповорачивают нациркулем до совпадения с осью ординат, отмечая точки.

4. В координатах по оси ординат вверх откладывают отрезок интегрирования. Из точкипроводят лучи, соединяя найденные точкис точкой:,, ….

5. На искомом графике проводят линиипараллельные в пределах соответствующего интервала лучам,, …. Первый отрезок проводят через начало координат, следующие отрезки соответственно через точку, затеми.т.д.

6. Ломаная линия дает приближенный график искомой функции, а ординаты в узловых точках соответствуют значению этой функции.

7. Полученные точки соединяют плавной кривой, это и есть график . Подсчитывают масштаб:.

Вывод масштабной формулы:

Кривая изображена в масштабепо оси ординат и- по оси абсцисс. Искомая функцияможет быть найдена по соотношению:.

В каждом интервале, например от доможно приближенно считать, что

, (1)

т.е. можно принять, что площадь криволинейной трапеции равновелика площади прямоугольника высотой и основанием.

Лучи ,, …образуют с положительным направлением оси абсцисс углы, причем

. (2)

Так как на искомом графике проводят линии параллельные лучам,, …. в пределах соответствующих интервалов, то эти линии наклонены относительно положительного направления оси абсцисс под такими же угламипричем

. (3)

приравниваем правые части соотношений (2) и (3):

или. (4)

Т.к. по Рис.

, (5)

то, подставив в (5) соотношения (4) и учитывая, что отрезки на графиках связанны с соответствующими физическими величинами с помощью масштабов соотношениями:

(5)

Получают

(6)

где: .

Соответственно масштаб искомого графика:

.

II. Рассмотрим механизм, нагруженный силами и моментами, которые являются функциями только скорости, а приведенный момент инерции рассматриваемого механизма имеет постоянную величину.

Требуется определить закон движения начального звена, т. е. или. В качестве примеров можно привести турбогенераторы и гидрогенераторные агрегаты, грузоподъемные машины и станки, прокатные станы, центробежные насосы и воздуходувки с электроприводом, следящие системы с электромоторным приводом и др.

Приведение сил и масс осуществляется так же, как и в случае, рассмотренном выше, а для решения поставленной задачи целесообразно воспользоваться уравнением движения в дифференциальной форме:

,

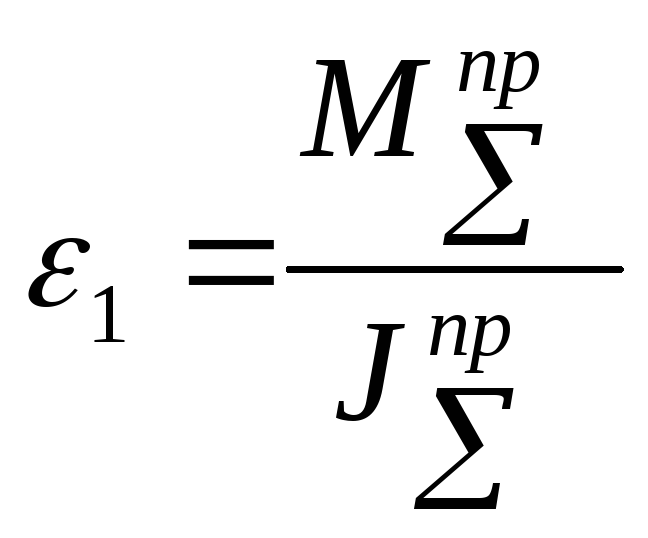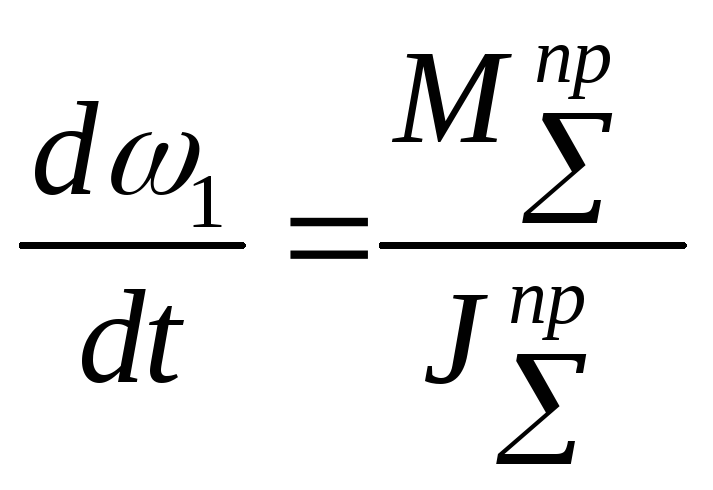т.к. , то, тогда. Так как, то, разделяем переменные и интегрируем с учетом того, что:

.

Из этого уравнения определяется закон изменения скорости звена приведения . При этом необходимоподставлять в уравнение с учетом знака.

III.Рассмотрим более общий случай динамического исследования когда силы и моменты приложенные к механизму, являются как функциямиперемещения, так и функциямискорости, а приведенный момент инерции механизма – величинапеременная.

Примерами такого режима работы могут служить технологические машины с электроприводами (металлорежущие станки, ковочные прессы и пр.), различные приборы с электромагнитным приводом (реле, средства автоматической защиты); сюда же относятся изучение таких процессов как запуск ДВС от электростартера и др.

Поставленная задача решается также при помощи уравнения движения в интегральной форме. Особенности решения заключаются в том, что работа сил, зависящих только от положения, отделяется от работы сил, зависящих от скорости. Поэтому и приведение этих двух видов сил осуществляется раздельно.