электротехникА и ЭЛЕКТРОНИКА

Лекции Князьковой Т.О.

МОДУЛЬ 2. «Линейные электрические цепи переменного тока. Переходные процессы»

Лекция 4 Однофазные электрические цепи синусоидального тока

Современная электроэнергетика базируется в основном на переменном токе. Внедрение переменного тока в практику относится к 70-ым годам 19 века.

По сравнению с другими токами синусоидальный имеет ряд преимуществ, которые позволяют экономично осуществляет производство, передачу, распределение и использование электрической энергии. В настоящее время производство и передача электрической энергии осуществляются при помощи трехфазного тока с частотой 50 Гц во всех странах мира кроме США и Японии (60Гц).

Различные области техники используют широкий диапазон частот синусоидального тока, в зависимости от технических потребностей. Так в авиации применяют синусоидальный ток с частотой 400 Гц, так как при этом снижаются габаритные размеры и вес оборудования. В электротермических установках используют диапазон частот от 500Гц до 50МГц. Частоты от долей Гц до 10ГГц применяют в радиотехнике.

Но с использованием синусоидального тока появляются электромагнитные процессы, оказывающие влияние на электрические цепи более сложного характера, чем в цепях постоянного тока. Появляется ряд особенностей в работе, например, конденсатора и катушки индуктивности. Переменный ток порождает в этих элементах переменные электрическое и магнитное поля. В результате возникают явление самоиндукции в дросселе и токи смещения в конденсаторе, которые оказывают существенное влияние на процессы в сложных электрических цепях.

Параметры синусоидальных электрических величин

Синусоидальная функция является периодической функцией времени, т.е. через равный промежуток времени, называемый периодом T, цикл колебаний повторяется.

i(t) = i(t + T), где i - мгновенное значение тока

Периоду Т соответствует фазовый угол 2π или 360°. Длительность времени периода Т измеряется в секундах.

Величина обратная периоду Т называют частотой и измеряется в Гц (число периодов в секунду)

также используется угловая частота ω =2πƒ (рад/сек) показывающая насколько фазовый угол синусоиды изменился за период, т.е. скорость изменения фазового угла синусоиды.

Аналитическое выражение мгновенных значений тока, ЭДС и напряжения определяется тригонометрической функцией:

i(t) = I_m sin(ωt + ψ_i)

u(t) = U_m sin(ω t + ψ_u)

e(t) = E_m sin(ωt + ψ_e),

где I_m, U_m, E_m – амплитудные значения тока, напряжения и ЭДС;

(ωt + ψ) – аргумент синуса, который определяют фазовый угол синусоидальной функции в данный момент времени t;Ψ – начальная фаза синусоиды, при t = 0

По ГОСТу ƒ = 50 Гц, следовательно, ω = 2πƒ = 314 рад/сек.

Временную функцию можно представить в виде временной диаграммы, которая полностью описывает гармоническую функцию, т.е. дает представление о начальной фазе, амплитуде и периоде (частоте). Временные диаграммы можно наблюдать с помощью специального прибора – осциллографа.

Рассмотрим пример:

Рис.4

Функция тока i(t) сдвинута вправо от начала координат, это означает, что начальная фаза имеет отрицательный угол, ток появляется раньше на ψi относительно начала координат. Ток опережает начало координат Но аналитическое выражение запишется следующим образом: i(t) = Im sin(ωt + ψi),

Знак «+» или «–» перед начальной фазой показывает, сколько не хватает градусов, чтобы наша функция выходила из начала координат. Начальную фазу отсчитывают от начала синусоиды, при t = 0, до начала координат.

Все сказанное выше относится и к функциям напряжения u(t) и ЭДС e(t)

При рассмотрении нескольких функций электрических величин одной частоты интересуются фазовыми соотношениями, называемой углом сдвига фаз.

Угол сдвига фаз φ двух функций определяют как разность их начальных фаз φ = ψ_u - ψ_i

• Если начальные фазы одинаковые, то φ = 0, тогда функции совпадают по фазе;

• Если φ = ± π, то функции противоположны по фазе.

Особый интерес представляет угол сдвига фаз между напряжением и током рис.5

Рис.5

На практике используют не мгновенные значения электрических величин, а действующие значения. Действующим значением называют среднеквадратичное значение переменной электрической величины за период. Обозначается той же буквой, что и амплитудное значение, но без индекса.

Для синусоидальных величин действующие значения меньше амплитудных в раз, т.е.

Электроизмерительные приборы градуируются в действующих значениях.

Часто для технических расчетов необходимо знать среднее значение электрических величин, но его берут за половину периода, так как при определении среднего значения за период у синусоидальной функции получается 0.

Следует обратить внимание на то, что среднее значение меньше действующего.

Применение комплексных чисел для расчета электрических цепей

Расчет электрических цепей с использованием тригонометрических функций весьма сложен и громоздок, поэтому при расчете электрических цепей синусоидального тока используют математический аппарат комплексных чисел.

Модуль комплексной амплитуды равен амплитуде синусоидальной величины, а аргумент – ее начальной фазе.

Вводится понятие комплексного величин амплитуд и действующих значений тока, напряжения, ЭДС и т.д.

Комплексные действующие значения пропорциональны комплексным амплитудам и записываются в виде:

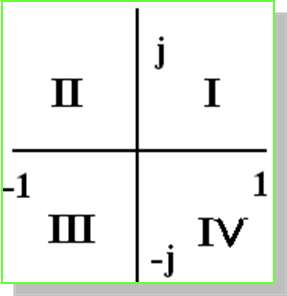
Синусоидальные электрические величины, представленные в комплексной форме, можно изображать графически. На комплексной плоскости в системе координат с осями +1 и +j, которыми обозначены положительные действительная и мнимая полуоси, строятся комплексные векторы. Длина вектора пропорциональна модулю действующих значений. Угловое положение вектора определяется аргументом комплексного числа. При этом отсчет положительного угла ведется против часовой стрелки от положительной действительной полуоси. Комплексная плоскость разбивается на четыре четверти:

Итак, рассмотрим нашу тригонометрическую функцию A(t) представленную в виде комплексной величины на комплексной плоскости. Получается, что наша функция представлена в виде вектора вращающегося на комплексной плоскости против часовой стрелки со скоростью ω, как показано на рис.1.

Рис.1

Из рис.1 видно, что вектор на комплексной плоскости можно построить двумя способами, первый, зная размер вектора и угол, и второй способ, зная координаты вектора по действительной и мнимой осям.

Первый способ это показательная форма представления комплексного числа, т.е.

,

где - комплексная величина, А - модуль комплексного числа или действующее значение величины, ψ_а - аргумент комплексного числа

Второй способ алгебраическая форма представления комплексного числа:

= а₁+jа₂,

где а₁ = Асоs ψ_а а₂ = Аsin ψ_а

Правила перехода из одной формы в другую.

Переход из показательной формы в алгебраическую форму:

дано

Используется формула Эйлера = соsψ_a + jsinψ_a

= А(соsψ_a + jsinψ_a) = Асоs ψ_а + jАsin ψ

Переход из алгебраической формы в показательную форму:

_{дано = Асоs ψа + jАsin ψа}

Рис. 2

Из рис.2 видно, вектор образует с осью координат прямоугольный треугольник, поэтому воспользуемся теоремой Пифагора, и найдем размер вектора, который равен гипотенузе треугольника:

причем особое внимание уделим углу – аргументу ψ_а модуля комплексного числа:

если вектор находится во второй и третьей четвертях комплексной плоскости, то к полученному значению аргумента необходимо прибавить 180° или π.

Если а₁ = 0, то комплексное число называется мнимым, аргумент ψ_а = ± 90°

Если а₂ = 0, то комплексное число называется действительным, ψ_а = 0, ± π

Простейшие математические операции с комплексными числами

Простейшие математические операции такие, как сложение, вычитание, умножение и деление проводятся с комплексными числами следующим образом: сложение и вычитание удобно проводить в алгебраической форме, а умножение и деление в показательной.

Единичные комплексы	действия с j
1; -1 ;	j·j = -1; j·(-j) =1 ;

Векторные диаграммы

Геометрический образ комплексных величин синусоидальных функций на комплексной плоскости называют векторной диаграммой. Векторные диаграммы широко используют для анализа электрических цепей.

Рассмотрим пример:

Дано: ;

Построим векторную диаграмму на комплексной плоскости:

Анализируя векторную диаграмму можно сделать вывод, что функция тока опережает функцию напряжения на угол 90°.

Точно так же будет выглядеть векторная диаграмма действующих значений

Только размеры векторов уменьшаться в раз.

Рассмотрим второй пример:

На рис.3 показан узел электрической цепи и приведена векторная диаграмма токов. Необходимо определить ток I₀ и построить векторную диаграмму токов.

Рис.3

Ток ₀ по известным токам ₁ и ₂ на векторной диаграмме определяется в соответствии с первым законом Кирхгофа по правилу параллелограмма.

Сопоставление диаграмм доказывает важность фазовых соотношений в цепях переменного тока, потому что, при неизмененных амплитудах (действующих значениях) суммируемых токов или напряжений результирующие величины этих токов и напряжений существенно отличаются по амплитудам за счет различия в фазовых соотношениях.